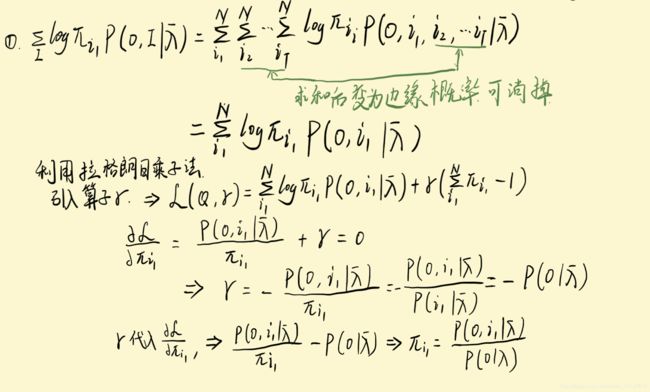机器学习基础——隐马尔可夫模型

隐马尔可夫模型

• 定义：隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。
  

• 对该问题中的数据进行数学定义

• 所有可能的状态集合$Q$，其中$N$为所有可能的状态数：
  $$Q=\{q_1,q_2,...,q_N\}$$

• 所有可能的观测集合$V$，其中$M$为所有可能的观测数：
  $$V=\{v_1,v_2,...,v_M\}$$

• 长度为$T$的状态序列$I$：
  $$I=(i_1,i_2,...i_T)$$

• 长度为$T$的观测序列$O$:
  $$O=(o_1,o_2,...,o_T)$$

1.模型定义

隐马尔可夫模型立足于两个基本假设：齐次马尔可夫性假设，观测独立性假设。

• 齐次马尔可夫性假设： 假设隐藏的马尔科夫链在任意时刻$t$的状态只依赖于前一时刻的状态，与其他时刻的状态及观测无关，也与时刻$t$无关。数学表示如下：
  $$P(i_t|i_{t-1},o_{t-1},...i_1,o_1)=P(i_t|i_{t-1}),t=1,2,...T$$
• 观测独立性假设： 即假设任意时刻的观测只能依赖于该时刻的马尔科夫链的状态，与其他观测及状态无关。数学表示如下：
  $$P(o_t|i_T,o_T,i_{T-1},o_{T-1},...,i_{t+1},o_{t+1},i_t,i_{t-1},o_{t-1},...i_1,o_1)=P(o_t|i_t)$$
  基于两个基本假设，我们建立状态转移概率矩阵$A$和观测概率矩阵$B$。
• 状态转移概率矩阵$A$：
  $$A=[a_{ij}{]}_{N\times N}$$
  式中，$a_{ij}$表示由状态$q_i$转移到状态$q_j$的概率。数学表示如下：
  $$a_{ij}=P(i_{t+1}=q_j|i_t=q_i)$$
• 观测概率矩阵$B$:
  $$B=[b_j(k){]}_{N\times M}$$
  $式中，b_j(k)表示状态为q_j时，观测为v_k的概率。数学表示如下：$
  $$b_j(k)=P(o_t=v_k|i_t=q_j)$$
  $对已有的矩阵A和B，补充初始状态概率即可构成闭合问题。定义初始状态台率向量\pi ：$
  $$\pi =({\pi }_i)$$
  ${\pi }_i表示t=1时刻处于状态q_i的概率。数学表示如下：$
  $${\pi }_i=P(i_1=q_i)$$
  $对构成的闭合问题，\pi 和A可以决定状态序列，B可以决定观测序列，所以隐马尔可夫模型可以表示为：$
  $$\lambda =(A,B,\pi )$$

2.隐马尔可夫模型的3个基本问题

• 1.概率计算问题。给定模型$\lambda =(A,B,\pi )$和观测序列$O=(o_1,o_2,...o_T)$，计算在模型$\lambda$下观测序列$O$出现的概率$P(O|\lambda )$.
• 2.学习问题。已知观测序列$O=(o_1,o_2,...o_T)$，估计模型$\lambda =(A,,B,\pi )$参数，使得在该模型下观测序列概率$P(O|\lambda )$最大，即用极大似然估计的方法估计参数。
• 3.解码问题。已知模型$\lambda =(A,B,\pi )$和观测序列$O=(o_1,o_2,...o_T)$，求对给定观测序列条件概率$P(I|O)$最大的状态序列$I=(i_1,i_2,...,i_T)$，即给定观测序列，求最有可能的对应的状态序列。
• 其中，解码问题常常被用来解决序列标注问题，假设给定了一段文本，这段文本可以视为马尔科夫链，文本为观测序列，文字的词性即为状态，构成状态序列，序列标注问题就是求出模型$\lambda$后，求出最有可能的状态序列，即求出词性序列。

2.1 概率计算问题

本文重点讨论解码问题，即序列标注问题，概率计算问题不是我们关注的重点，不过概率计算问题中引入的前向概率和后向概率值得学习，所以本节仍做讲解。
概率计算问题是已知$\lambda$和$O$，求$O$出现的概率。数学表示为：
$$P(O|\lambda )$$
对观测概率的计算离不开状态序列，设状态序列为$I=(i_1,i_2,...,i_T)$，$I$的概率是：
$$P(I|\lambda )={\pi }_{i_1}{a}_{i_1{i}_2}{a}_{i_2{i}_3}....a_{i_{T-1}{i}_T}$$
在该状态序列下，观测序列$O=(o_1,o_2,...o_T)$出现的概率为:
$$P(O|I,\lambda )=b_{i_1}(o_1)b_{i_2}(o_2)...b_{i_T}(o_T)$$
由以上两式，可计算联合概率分布$P(O,I|\lambda )$，即给定模型参数时，状态序列$I,O$同时出现的概率：
$$P(O,I|\lambda )=P(I|\lambda )P(O|I,\lambda )={\pi }_{i_1}{b}_{i_1}(o_1)a_{i_1{i}_2}{b}_{i_2}(o_2).....a_{i_{T-1}{i}_T}{b}_{i_T}(o_T)$$
由此，可通过对所有可能的状态序列$I$求和，就可以计算出边缘概率分布$P(O|\lambda )$，即：
$$P(O,I|\lambda )=\sum _{I}P(I|\lambda )P(O|I,\lambda )=\sum _{i_1,i_2,...i_T}{\pi }_{i_1}{b}_{i_1}(o_1)a_{i_1{i}_2}{b}_{i_2}(o_2).....a_{i_{T-1}{i}_T}{b}_{i_T}(o_T)$$
每一时刻的状态$i$有$N$种可能，所以该算法的计算复杂度为$O(T{N}^T)$，为避免如此复杂的计算，引入前向算法和后向算法。

2.1.1 前向算法

• 首先定义前向概率：给定到$t$时刻，部分观测序列为$o_1,o_2,...o_t$，且$t$时刻状态为$q_i$的概率为前向概率，数学表示为：
  $${\alpha }_t(i)=P(o_1,o_2,...,o_t,i_t=q_t|\lambda )$$
  由此，给出递推公式：
  $$\begin{gathered} 初值：{\alpha }_1(i)={\pi }_i{b}_1(o_1),i=1,2,....N \\ 递推:{\alpha }_{t+1}(i)=[\sum _{j=1}^N{\alpha }_t(j)]a_{ji}{b}_{t+1}(o_{t+1}),t=1,2,...T-1 \\ 终止：P(O|\lambda )=\sum _i^N{\alpha }_T(i) \end{gathered}$$
  这里需要注意，在第一步中没有计算所有状态出现的概率和，是因为在计算${\alpha }_2(i)$时，会计算$t=1$时刻的所有状态出现的概率和；在递推过程中，执行到最后一项，得到${\alpha }_T(i)$，但是我们需要计算的是$O$出现的概率，所以需要对所有可能的状态相加，得到边缘概率分布。

2.1.2 后向算法

• 后向概率：给定隐马尔可夫模型$\lambda$，在时刻$t$状态为$q_i$的条件下，从$t+1$到$T$的部分观测序列为$o_{t+1},...o_T$的概率为后向概率，数学表示为：
  $${\beta }_t(i)=P(o_{t+1},...o_T|i_t=q_i,\lambda )$$
• 由此给出递推公式：
  $$\begin{gathered} 初始化：{\beta }_T(i)=1 \\ 递推：{\beta }_t(i)=\sum _{j=1}^N{a}_{ij}{b}_t(o_t){\beta }_{t+1}(j),t=1,2,...T-1 \\ 终止：P(O|\lambda )=\sum _{i=1}^N{\pi }_i{b}_1(o_1){\beta }_1(i) \end{gathered}$$

2.13 概率给出

根据前项公式和后向公式，可以给出$O$出现的概率计算公式：
$$\begin{gathered} P(O|\lambda )=\sum _{i=1}^N{\alpha }_T(i)=\sum _{i=1}^N{\pi }_i{b}_1(o_1){\beta }_1(i)=\sum _{i=1}^N{\alpha }_t(i){\beta }_t(i) \\ =\sum _{i=1}^N\sum _{j=1}^N{\alpha }_t(i)a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j) \end{gathered}$$

2.2 学习算法

2.2.1 监督学习方法

假设训练数据包含S个长度相同的观测序列和对应的状态序列$\{(O_1,I_1),(O_2,I_2),...,(O_s,I_s)\}$,可以利用极大似然估计法来估计隐马尔可夫模型的参数。

• 转移概率$a_{ij}$的估计
  $${\hat{a}}_{ij}=\frac{A_{ij}}{{\sum }_{j=1}^N{A}_{ij}},i=1,2,...N;j=1,2,...N$$
  $A_{ij}$为由状态$i$向状态$j$转移的频数。
• 观测概率$b_j(k)$的估计
  $${\hat{b}}_j(k)=\frac{B_{jk}}{{\sum }_{k=1}^M{B}_{jk}},j=1,2,...N;k=1,2,...,M$$
  $B_{jk}$为状态为$j$，观测为$k$的频数。
• 初始状态概率${\pi }_i$的估计
  $$\widehat{{\pi }_i}=\frac{Q_i}{S},i=1,2,...,N$$
  $Q_i$为初始状态为$q_i$的频数，$S$为样本数量。

2.2.2 无监督学习方法

这一部分式子太多了，改手写吧。。。字难看，各位见谅。

• 无监督学习使用著名的baum-welch算法，该方法后来被证明为使EM算法。
  算法同EM算法相同，分两步：E步和M步。E步求期望，M步最大化模型参数。

2.2.2.1 E步求期望

E步是指在给定当前模型参数$\bar{\lambda }$和观测数据$O$的条件下，求完全数据$O,I$的对数似然概率关于未知数据$I$的期望。数学表示及推导见下图，各位见谅。。。

2.2.2.2 M步最大化模型参数

2.3 解码方法

• 设在$t$状态为$i$的所有单个路径$(i_1,i_2,...i_T)$中概率最大值为${\delta }_t(i)$。数学表示为：
  $${\delta }_t(i)=\max P(i_t=i,i_{t-1},...,i_1,o_t,...,o_1|\lambda ),i=1,2,...N$$
  递推：
  $$\begin{gathered} 初始：{\delta }_1(i)={\pi }_i{b}_i(o_1),i=1,2,...,N \\ 递推：{\delta }_{t+1}(i)=\underset{1\le j\le N}{\max }[{\delta }_t(j)a_{ji}]b_i(o_{t+1}) \end{gathered}$$
• 设在时刻$t$状态为$i$的所有单个路径$(i_1,i_2,...,i_{t-1},i)$中概率最大的路径第$t-1$个结点为${\Psi }_t(i)$，数学表示为：
  $${\Psi }_t(i)=\arg \underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)a_{ji}]$$
  递推：
  $$\begin{gathered} 初始：{\Psi }_1(i)=0 \\ 递推：{\Psi }_t(i)=\arg \underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)a_{ji}] \end{gathered}$$

2.3.1 维特比算法求解过程

初始化（t=1）:
$$\begin{gathered} {\delta }_1(i)={\pi }_i{b}_i(o_1),i=1,2,...,N \\ {\Psi }_1(i)=0 \end{gathered}$$
递推t=2,…,T：
$$\begin{gathered} {\delta }_t(i)=\underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)a_{ji}]b_i(o_t) \\ {\Psi }_t(i)=\arg \underset{1\le j\le N}{\max }[{\delta }_{t-1}(j)a_{ji}] \end{gathered}$$
终止：
$$i_T^{\ast }=\arg \underset{1\le i\le N}{\max }[{\delta }_T(i)]$$
最优路径回溯$t=T-1,...,2,1$：
$$i_t^{\ast }={\Psi }_{i+1}(i_{t+1}^{\ast })$$