Day11-13.数组拓展：数组中常见排序算法

目录

数组的常见排序算法

冒泡排序（Bubble Sort）

选择排序（Selection Sort）

插入排序（Insertion Sort）

希尔排序（Shell Sort） [较难]

快速排序（Quick Sort）

归并排序(Marge Sort)

基数排序（Radix Sort）

堆排序（Heap Sort）

参考资料、视频教学 

---

数组的常见排序算法

1.冒泡排序 2.选择排序 3.插入排序 4.希尔排序 5.快速排序 6.归并排序 7.基数排序 8.堆排序

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
• 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。 

• 算法复杂度： 

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
• 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
• 时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
• 空间复杂度：是指算法在计算机

内执行时所需存储空间的度量，它也是数据规模n的函数。 

冒泡排序（Bubble Sort）

• 排序原理：将数组元素两两比较，交换位置，大元素往后放，经过一轮比较后，最大的元素，就会出现在最大的索引处。

• 冒泡排序无疑是最为出名的牌算法之一。

• 冒泡的代码很简单，两层循环，外层冒泡轮数，里层依次比较，人尽皆知。

• 当我们看到嵌套循环，应该立马就可以得出这个算法的时间复杂度为O(n2)。

• 思考：如何优化？

    public static void main(String[] args) {
        int[] a ={6,5,3,4,2,1};
        System.out.println(Arrays.toString(sort(a)));
    }

    //冒泡排序
    //1.比较数组中相邻的两个元素，如果第一个逼第二个数大，我们就交换位置
    //2.每一次比较，都会产生一个最大，或者最小的数字
    //3.下一轮可以少一次排序！
    //4.依次循环，直到结束！

    public static int[] sort(int[] array){
        int number = 0;  //记录循环次数，测试是否优化
        //外层循环，判断我们这个要走多少次；
        for(int i = 0;i array[j]){   //相邻元素两两对比
                    int temp =array[j];    //创建一个临时变量
                    array[j] = array[j+1]; 
                    array[j+1] = temp;
                    mark = true;  //发生交换后，mark变为true
                }
                number++; //循环次数+1
            }
            if(mark == false){  //如果没有发生交换，说明已经数组有序，结束循环
                break;
            }
        }
        System.out.println("当前循环次数为:"+ number);
        return array;
    }

选择排序（Selection Sort）

• 排序原理1：首先在未排序序列中找到最小大元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。 
• 排序原理2：从0索引处开始，依次与后边的元素进行比较，找到比索引处小的数进行互换
• 以上二种原理何者正确有待考证，下方动图为原理1演示。

    //排序原理1
    public static int[] sort_1(int[] arr){
        for (int i = 0;i

插入排序（Insertion Sort）

• 排序原理：直接插入排序是一种最简单的排序方法，将一个记录插入到一个长为m的有序列表中，使之仍保持排序

    public static int[] sort(int[] array){

        //直接插入排序:从1索引处开始，将后面的元素插入之前的有序列表中，使之仍保持有序
        //外层循环定义轮次
        for(int a =1; a < array.length; a++){
            //里层循环比较插入
            int b = a;  //定义变量b是因为防止a--与a++冲突
            while(array[b]0){  //b>0,b有可能因--小于0
                int temp = array[b];
                array[b] = array[b-1];
                array[b-1] = temp;
                b = b-1;
            }
        }
        return array;
    }


    //该代码也可由两层for循环实现
    public static int[] sort_1(int[] array){
        //外层循环定义轮次
        for (int a = 1; a < array.length; a++) {
        //a=1,因为要从第二个元素进行插入排序。第一个元素可以认为已经被排序。
            for(int b = a ; b >0; b--){  //相当于简化了while循环，int b=a
                if(array[b] < array[b-1]){
                //b-1 因为已经与上一位进行了交换，要继续与前一位进行比较
                    swapValue(array,b,b = b-1);    //调用交换方法
                }
            }
        }
        return array;
    }
    public static void swapValue(int[] arr, int i,int j){
        //交换值的方法
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }
    

希尔排序（Shell Sort） [较难]

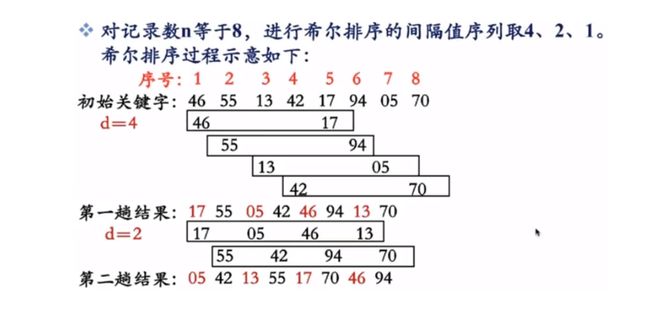
• 排序原理：希尔排序又称缩小增量排序。先将原表按增量ht分组，每个子文件按照直接插入法排序。同样，用下一个增量ht除以2，将文件再分为子文件，再用直接插入法排序。直到ht=1时将整个文件排好序。
• 关键：选择合适的排序增量。
• 希尔排序算法9-3：可以通过三重循环实现 

希尔排序音计算机科学家Shell而得名。是对插入排序的优化。希尔排序又叫缩小增量排序

插入排序其实就是增量为1的希尔排序。

• 代码实现：

    public static void main(String[] args) {
        int[] a ={46,55,13,42,17,94,5,70};
        shellSort_1(a);
        System.out.println(Arrays.toString(a));
    }
    //希尔排序：它是对插入排序的一个优化，核心的思想就是合理地选取增量，经过一轮排序后，就会让序列大致有序
    //然后再不断的缩小增量，进行插入排序，直到增量为1，整个排序结束

    public static void shellSort_1(int[] arr){
        //定义一个增量
        int h=4;
        for(int i = h; i < arr.length; i++){
            for(int j = i ; j-h >=0 ; j = j-h){
                //!因为交换过的数要继续与前面的数进行比对，所以判断j-h之后是否还存在元素，j-h >=0，0为数组中最小下标
                if(arr[j] < arr[j-h]){      
                    swapValue(arr,j,j-h);     //调用交换方法
                }
            }
        }
        //第一次结果:[17, 55, 5, 42, 46, 94, 13, 70]

        //第二轮
        h = 2;
        for(int i = h; i < arr.length; i++){
            for(int j = i ;j > h-1; j-=h){  //j > h-1是教程中的写法，等于j-h >=0
                if(arr[j] < arr[j-h]){
                    swapValue(arr,j,j-h);
                }
            }
        }
        //第二轮结果:[5, 42, 13, 55, 17, 70, 46, 94]

        //第三轮
        h = 1;
        for(int i = h; i < arr.length; i++){
            for(int j = i ;j > h-1; j-=h){
                if(arr[j] < arr[j-h]){
                    swapValue(arr,j,j-h);
                }
            }
        }
        //第三轮结果:[5, 13, 17, 42, 46, 55, 70, 94] 增量为1，排序完毕。
    }

    /*
    第一次错误是因为错误将j-=h理解为j=h-1。 j-=h 等于 j = h-h;
    第二次疑惑是错误理解for循环。for(初始化;布尔表达式;更新)，初始化只会进行一次
    第二次疑惑是因为不理解嵌套循环for(int j = i ;j > h-1; j-=h)中判断语句j > h-1。 j>h-1 等同于 j-h >=0 0为数组最小下标
     */
    //未完
    

    /*
    错误总结：
    第一次错误是因为错误将j-=h理解为j=h-1。 j-=h 等于 j = h-h;
    第二次疑惑是因为错误理解for循环。for(初始化;布尔表达式;更新)，初始化只会进行一次
    第三次疑惑是因为不理解嵌套循环for(int j = i ;j > h-1; j-=h)中的判断语句j > h-1。
    j>h-1 等同于 j-h >=0，0为数组最小下标
     */

    public static void swapValue(int[] arr, int i,int j){
        //交换值的方法
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

• 继续优化： 增量改为数组长度的一半  →  使用克努特序列。

• 增量的选择：Knuth序列 （克努特序列）
• h=1 ，h= 3*h +1
• 代码实现：

      public static void main(String[] args) {
        int[] a ={46,55,13,42,17,94,5,70,9,5,6,89,50,50,255};
        shellSort_3(a);
        System.out.println(Arrays.toString(a));
    }


    //由上面代码进行优化
    //希尔排序的思想，合理的选取这个增量
    //第一次这个增量选取数组长度的一半，然后不断减半
    public static void shellSort_2(int[] arr){
        for(int h =arr.length/2 ; h>0; h = h/2){
            for(int i = h; i < arr.length; i++){
                for(int j = i ;j > h-1; j-=h){      //判断是否还能继续交换
                    if(arr[j] < arr[j-h]){
                        swapValue(arr,j,j-h);
                    }
                }
            }
        }
    }

    //我们第一次的增量选择数组长度的的一半，还不是很好，我们可以使用一种序列，克努特序列
    //int h=1;
    //h = h*3+1;
    //根据克努特序列选取我们第一次的增量
    public static void shellSort_3(int[] arr){
        int jianGe=1;
        while(jianGe <=arr.length/3){
            jianGe = jianGe*3+1;
        }
        //System.out.println(jianGe); //测试第一次选出的jianGe

        for(int h =jianGe ; h>0; h = (h-1)/3){
            // h=3*h+1为增加，反之h=(h-1)/3为减少,希尔排序需要减少到间隔为1
            for(int i = h; i < arr.length; i++){
                for(int j = i ;j -h >=0 ; j = j -h){      //判断是否还能继续交换
                    if(arr[j] < arr[j-h]){
                        swapValue(arr,j,j-h);
                    }
                }
            }
        }
        return arr;
    }


    public static void swapValue(int[] arr, int i,int j){
        //交换值的方法
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

注：实在不懂看视频 西部开源Java之数组与排序_哔哩哔哩_bilibili

快速排序（Quick Sort）

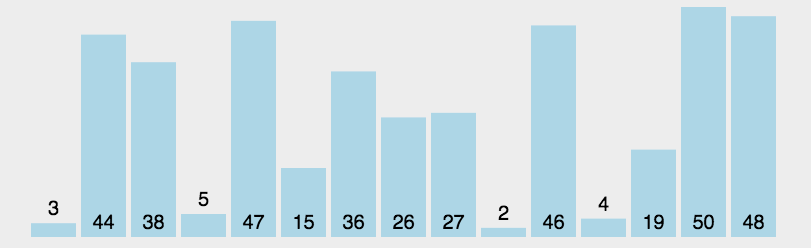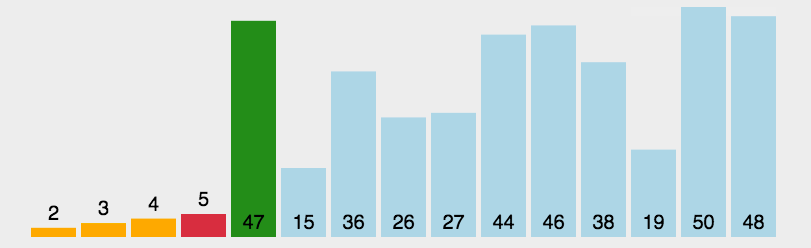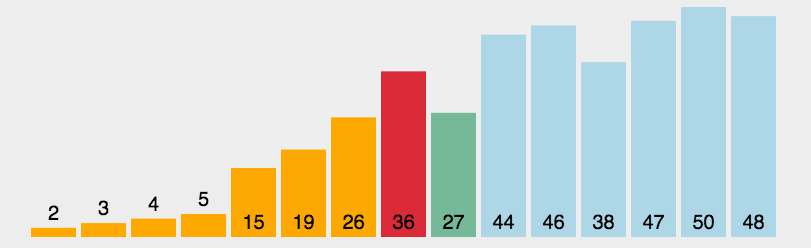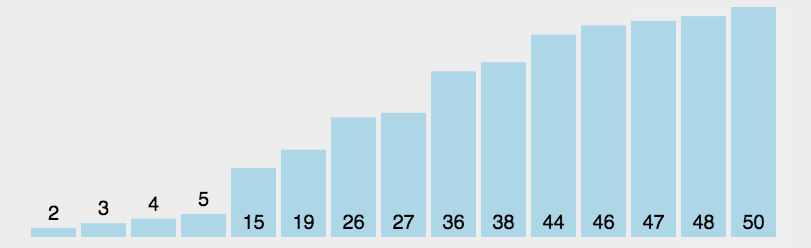
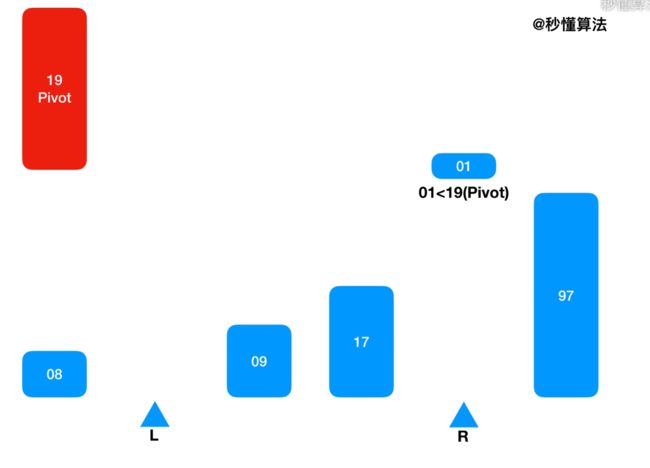
• 排序原理：分治法：比大小，再分区

1. 从数组中取出一个数，作为基准数(Pivot中心轴)。
2. 将大于Piveot的数字放在Pivot的右边
3. 将小于Piveot的数字放在Pivot的左边
4. 再对左右区间重复第二三步，直到各区间只有一个数。

• 挖坑填数

1. 将基准数挖出形成第一个坑。
2. 由后向前找比它小的数，找到后挖出此数填到前一个坑中。
3. 由前向后找比它大或等于它的数，找到后也挖出此数填到前一个坑中。
4. 重复执行2、3步骤。

• 代码实现：

    public static void main(String[] args) {

        int[] arr = {10, 3, 5, 6, 1, 0, 100, 40, 50, 8};
        //调用方法，进行快速排序，传入数组、起始位置、结束位置
        quickSort(arr, 0, arr.length - 1);

        System.out.println(Arrays.toString(arr));
    }   //[0, 1, 3, 5, 6, 8, 10, 40, 50, 100]

    public static void quickSort(int[] arr,int start,int end){
        if(start=P){       //L=P，该数比基准数大，继续循环向左查找 R--
            }
            if(L

参考   秒懂算法：快速排序算法_哔哩哔哩_bilibili

          西部开源：西部开源Java之数组与排序_哔哩哔哩_bilibili

归并排序(Marge Sort)

归并排序就是利用归并的思想实现排序的方法。

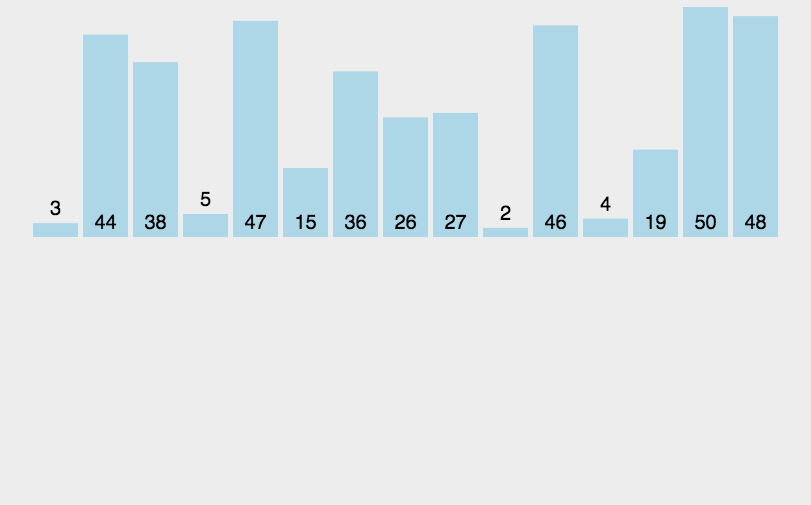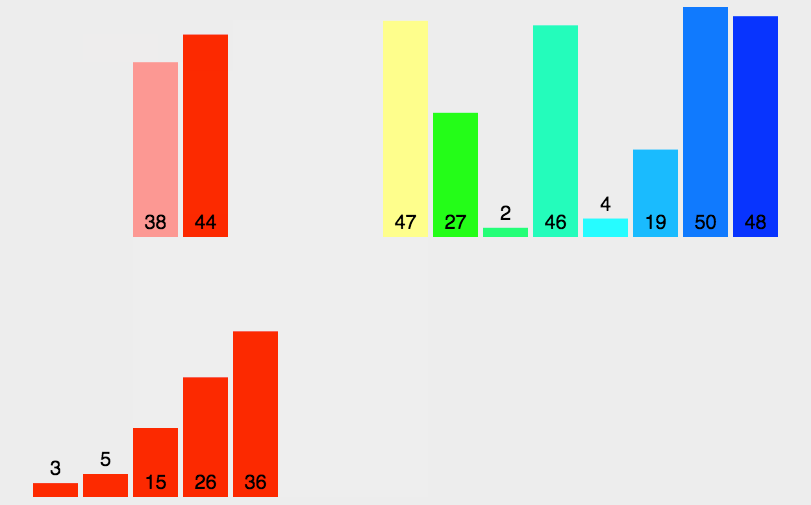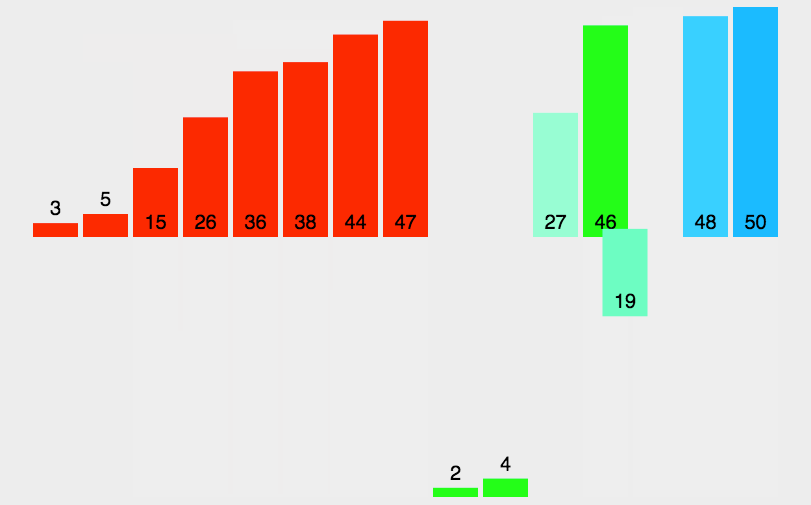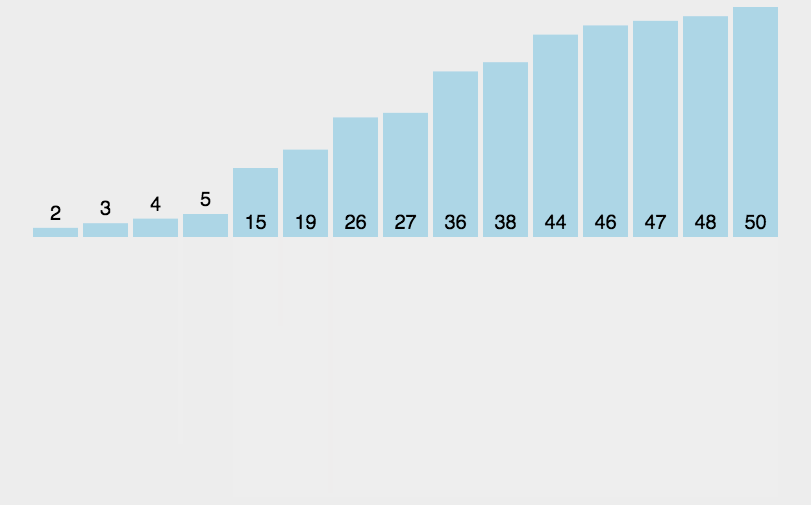
• 排序原理：假设初始序列有N个记录，则可以看成是N个有序的子序列，每个子序列的长度为1，然后两两归并，得到N/2长度为2或1的有序序列，再两两归并...如此重复，直到得到一个长度为N的有序序列为止。

• 算法描述：
• 把长度为n的输入序列分成两个长度为n/2的子序列；
• 对这两个子序列再分别采用归并排序；
• 将两个排序好的子序列合并成一个最终的排序序列。

• 代码实现：

    public static void main(String[] args) {
        //待排序数组
        int[] arr = {10, 30, 2, 1, 0, 8, 7, 5, 19, 29};


        //拆分
        chaiFen(arr,0,arr.length-1);
        //System.out.println(Arrays.toString(arr));
        // [0, 1, 2, 5, 7, 8, 10, 19, 29, 30]

        //归并
        //我们先给一个左右两边是有序的数组，先来进行归并操作
        //int[] arr={4,5,7,8,  1,2,3,6};
        //guiBing(arr,0,3,arr.length-1);

    }

    public static void chaiFen(int[] arr, int startIndex, int endIndex) {
        //计算中间索引
        int centerIndex = (startIndex + endIndex)/2;
        if(startIndex < endIndex){          //索引重合将不会继续拆分，也意味着不会进行归并浪费资源
            chaiFen(arr,startIndex,centerIndex);       //递归 拆左边
            chaiFen(arr,centerIndex+1,endIndex);       //递归 拆右边
            //拆分完毕后，归并、排序！
            guiBing(arr,startIndex,centerIndex,endIndex);
        }
    }
    public static void guiBing(int[] arr, int startIndex, int centerIndex, int endIndex) {
        //定义一个临时数组
        int[] tempArr= new int[endIndex -startIndex +1];

        int i=startIndex;            //定义左边数组的起始索引
        int j=centerIndex+1;         //定义右边数组的起始索引
        int index =0;                //定义临时数组的起始索引
        //比较左右两个数组的元素大小，往临时数组中放
        while (i<=centerIndex && j<=endIndex){      //如果两个数组都有剩余元素
            if(arr[i]

基数排序（Radix Sort）

• 基数排序不同于之前所介绍的各类排序。前面介绍到的排序方法或多或少是通过使用比较和移动记录来实现排序，而基数排序的实现不需要进行对关键字的比较，只需要对关键字进行“分配”与“收集”两种操作即可完成。
• 排序原理：基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。最后将元素取出完成排序。

• 代码实现：

    //基数排序:通过分配再收集的方式进行排序
    //注：该代码目前存在BUG，如数组中含有小数类型，则无法获取小数位上的数字。
    public static void main(String[] args){
        int[] arr = {2,1,5,21,31,444,23,33,47,10,903,124,987,100};
        //确定排序轮次，需要获取数组中最大值，查询其位数,确定循环轮次
        //int max = getMax(arr);
        //基数排序
        sortArray(arr);
        System.out.println(Arrays.toString(arr));

    }
    public static void sortArray(int[] arr) {
        int max = getMax(arr);
        int len = String.valueOf(max).length();
        //String.valueOf()可变量由基本数据类型转为String类型。
        //而String本质上是由char类型的数组组成
        //所以String.valueOf(max).length()可获取该数字位数

        //定义二维数组，放10个桶，每个最大容量为arr.length。 0-9
        int[][] tempArr = new int[10][arr.length];
        //定义统计数组，统计每个桶中元素个数
        int[] counts = new int[10];
        //循环轮次
        for(int i=0, n=1; i

堆排序（Heap Sort）

（待续）

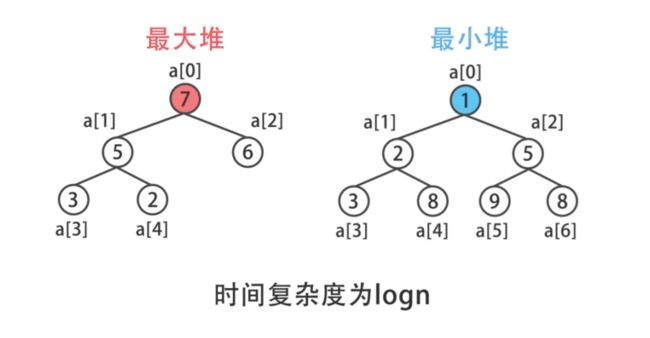
堆是一种特殊的树形数据结构

•  代码实现：

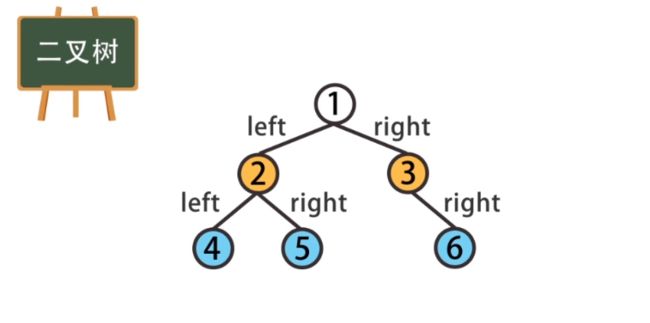
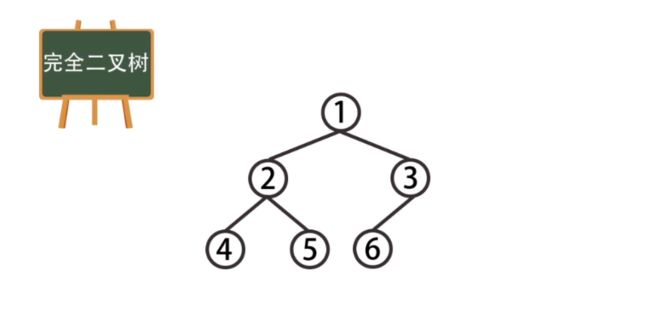
    //堆排序           二叉树 → 完全二叉树 → 最大堆、最小堆
    //parent = (i -1)/2
    //c1 = 2i +1            //子节点1
    //c2 = 2i +2            //子节点2
    public static void main(String[] args) {
        int[] arr = {10,5,8,3,4,6,7,1,2};
        int l = arr.length;
        heap_sort(arr,l);
        System.out.println(Arrays.toString(arr));

    }

    public static void heap_sort(int tree[],int n){
        build_heap(tree, n);             //先将无序数组变为 最大堆结构

        for(int i = n - 1; i >= 0; i--){
            swap(tree, i, 0);         //交换根节点与最后一个节点
            heapify(tree, i, 0);      //砍断  (减少节点数量)
        }
    }

    public static void build_heap(int tree[],int n){    //n:节点数量    build_heap:建造堆
        int last_node = n-1;            //最后一个节点
        int parent = (last_node-1)/2;   //最后一个节点的parent节点
        for (int i = parent; i>= 0; i--){       //由parent节点开始排序，形成 最大堆结构
            heapify(tree, n, i);
        }
    }

    //Heapify 是尝试将一整个数组构建成一个堆的方式，即通过调整自己，交换数组中的元素，就可以把自己整理成一个最大堆。
    public static void heapify(int[] tree, int n , int i){     //n:节点数量  i:当前堆调整的节点
        if(i >= n){         //
            return;
        }
        int c1 = 2 * i +1;      //c1:当前节点的子节点1
        int c2 = 2 * i +2;
        int maxIndex = i;       //默认最大值节点为 i

        if (c1 < n && tree[c1] > tree[maxIndex]) {        //比较、替换最大值节点
            maxIndex = c1;
        }
        if (c2 < n && tree[c2] > tree[maxIndex]) {
            maxIndex = c2;
        }
        if (maxIndex != i){
            swap(tree,maxIndex,i);
            heapify(tree, n, maxIndex);     //maxIndex节点变动后，其子节点也该重新排序
        }
    }
    //交换方法
    public static void swap(int[] arr,int i, int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

堆排序(heapsort)_哔哩哔哩_bilibili

参考资料、视频教学 

参考资料：十大经典排序算法（动图演示） - 一像素 - 博客园

视频教学：西部开源Java之数组与排序_哔哩哔哩_bilibili

                  快速排序算法_哔哩哔哩_bilibili 

                  堆排序(heapsort)_哔哩哔哩_bilibili