感知机:教你用Python一步步实现
感知机
问题描述
感知机是二类分类的线性分类模型,输入为分类对象的特诊向量,输出为 ± 1 \pm 1 ±1,用于判别分类对象的类型。这么说有些抽象,下面举一个例子。
就像上面这幅图,
- 实例对应上图就是每个点
- 实例的特征向量就是指这些点的横纵坐标,我们把他记为 ( x 1 , x 2 ) T (x_1, x_2)^T (x1,x2)T。
- 我们根据每个点的颜色,将点分别标记为 1 1 1和 − 1 -1 −1,也就是我们的输出 y y y 。
利用这些已知坐标的红蓝点,我们需要训练下面这个模型,
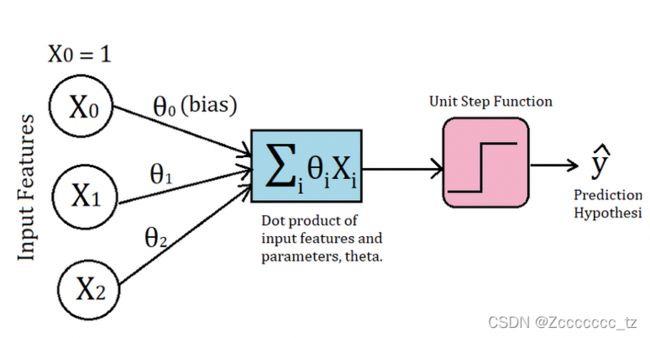
这个模型一共有 3 3 3个参数 ( θ 0 , θ 1 , θ 2 ) (\theta_0, \theta_1, \theta_2) (θ0,θ1,θ2),使它能够实现以下功能:
- 当 y = s i g n ( θ 1 x 1 + θ 2 x 2 + θ 0 ) = + 1 y={\rm sign}(\theta_1 x_1 + \theta_2 x_2 + \theta_0)=+1 y=sign(θ1x1+θ2x2+θ0)=+1时,我们知道该点为红。
- 当 y = s i g n ( θ 1 x 1 + θ 2 x 2 + θ 0 ) = − 1 y={\rm sign}(\theta_1 x_1 + \theta_2 x_2 + \theta_0)=-1 y=sign(θ1x1+θ2x2+θ0)=−1时,我们知道该点为蓝。
其中
s i g n ( x ) = { + 1 , x ≥ 0 − 1 , x < 0 \begin{aligned} {\rm sign}(x) = \left\{\begin{aligned} +1,&x \geq 0 \\ -1,&x<0 \end{aligned}\right. \end{aligned} sign(x)={+1,−1,x≥0x<0
数据集构建
开始前,我们需要自己整一个数据集用来训练。
先导入一些后面需要的包
import numpy as np
import matplotlib.pyplot as plt
import random
from typing import List, Tuple
然后就是搭建我们的数据集。
# 随机生成一些点,并根据直线将点划分为2个区域
def sample_point(w: float, b: float, num: int) -> Tuple[List[List[float]], List[float]]:
x, y = [], []
for _ in range(num):
p_x1 = np.random.random_sample(1) * 20 - 10
p_x2 = np.random.random_sample(1) * 20 - 10
p_y = 1 if w * p_x1 + b - p_x2 > 0 else -1
x.append([p_x1, p_x2])
y.append(p_y)
return x, y
# 先随机生成一条直线
w_ideal = np.random.random_sample(1) * 10 - 5
b_ideal = np.random.random_sample(1) * 10 - 5
x = np.linspace(-10, 10, 1000)
line_ideal = w_ideal * x + b_ideal
# 搭建数据集
sample_x, sample_y = sample_point(w_ideal, b_ideal, 500)
为了更加直观,我们可以将这些点用 matplotlib来可视化一下
# 可视化
plt.xlim(xmax=-10, xmin=10)
plt.ylim(ymax=-10, ymin=10)
plt.plot(x, line_ideal, 'g', linewidth=10)
for i, p_x in enumerate(sample_x):
if sample_y[i] == 1:
plt.scatter(p_x[0], p_x[1], c='r', alpha=0.3)
else:
plt.scatter(p_x[0], p_x[1], c='b', alpha=0.3)
plt.show()
我们会得到下面这张图片,
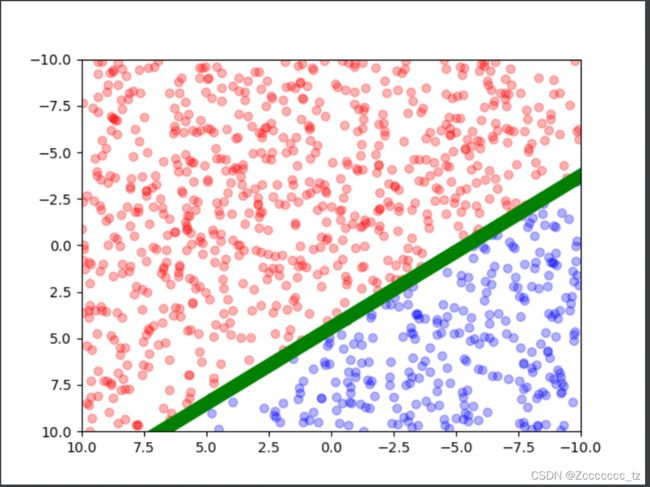
其中绿色的那条线,就是实际情况下可以区分红蓝点的直线。
下面我们要做的,就是假装不知道这条直线的参数,即代码中的w_ideal和b_ideal,看看我们能否从数据集中获得我们估计出来的参数,即w_est和b_ideal。
(有人可能要问了,我们上面不是说三个参数 ( θ 0 , θ 1 , θ 2 ) (\theta_0, \theta_1, \theta_2) (θ0,θ1,θ2)吗?怎么又变成估计两个参数了?不着急,后面会有介绍)。
模型训练
模型训练的理论支持
回到我们的问题,如何根据点的横纵坐标来实现点颜色的分类?
为了能够实现这个预测功能,我们知道,我们需要训练 3 3 3个参数 ( θ 0 , θ 1 , θ 2 ) (\theta_0, \theta_1, \theta_2) (θ0,θ1,θ2)。
假设我们现在有了这么一组参数 ( θ 0 ′ , θ 1 ′ , θ 2 ′ ) ({\theta}_0',{\theta}_1', {\theta}_2') (θ0′,θ1′,θ2′),如何衡量这一组参数的好坏呢?如果这一组参数还不够好,我们如何去优化这些参数呢?
于是,我们需要定义一个损失函数,用来衡量这个参数的好坏,并利用损失函数的梯度,将损失函数极小化。
损失函数的定义
直观来讲,一组好的参数应该满足不误分一个点,所以将分错点的个数作为损失函数是一个合理的想法。那么误分的点有什么特点呢?
y i ⋅ ( ∑ j = 1 θ j x i j + θ 0 ) ≤ 0 y_i \cdot (\sum_{j=1} \theta_{j} x_{ij} + \theta_0) \leq 0 yi⋅(j=1∑θjxij+θ0)≤0
对于第 i i i个样本而言,
- 当样本点为蓝色时, y i = − 1 y_i=-1 yi=−1,却被误分为红色,也就是 ∑ j = 1 θ j x i j + θ 0 ≥ 0 \sum_{j=1} \theta_{j} x_{ij} + \theta_0 \geq 0 ∑j=1θjxij+θ0≥0。
- 当样本点为红色时, y i = + 1 y_i=+1 yi=+1,却被误分为蓝色,也就是 ∑ j = 1 θ j x i j + θ 0 ≤ 0 \sum_{j=1} \theta_{j} x_{ij} + \theta_0 \leq 0 ∑j=1θjxij+θ0≤0。
综上,我们损失函数被定义为
L ( θ ) = − ∑ x i ∈ M y i ⋅ ( ∑ j = 1 θ j x i j + θ 0 ) = − ∑ x i ∈ M y i ⋅ ( θ x i ) \begin{aligned} \mathcal{L}(\theta) &= -\sum_{x_i \in M} y_i \cdot (\sum_{j=1} \theta_{j} x_{ij} + \theta_0) \\ &= -\sum_{x_i \in M} y_i \cdot (\theta x_i) \end{aligned} L(θ)=−xi∈M∑yi⋅(j=1∑θjxij+θ0)=−xi∈M∑yi⋅(θxi)
其中 M M M为被误分点的集合, θ x i = ∑ j = 0 θ j x i j , x i 0 = 1 \theta x_i = \sum_{j=0} \theta_{j} x_{ij}, x_{i0}=1 θxi=∑j=0θjxij,xi0=1。
利用损失函数优化参数
感知机学习算法是误分类驱动的,具体采用随机梯度下降法。我们首先随机选取一组参数 θ \theta θ,然后利用梯度下降法不断地极小化目标函数。
- 这里的极小化过程不是一次使所有误分类点的梯度下降,而是来一次随机选取一个误分类点使其梯度下降
- ▽ θ L ( θ ) = − ∑ x i ∈ M y i x i \bigtriangledown_\theta \mathcal{L}(\theta) = -\sum_{x_i\in M} y_ix_i ▽θL(θ)=−∑xi∈Myixi
- 随机选择一个误分类点,利用这个点对参数进行优化
- θ ← θ + η y i x i \theta \leftarrow \theta + \eta y_i x_i θ←θ+ηyixi
- η \eta η是学习率,取值范围为 [ 0 , 1 ] [0,1] [0,1]
Python代码的实现
def perceptron(x, y, lr, t) -> Tuple[np.ndarray, List[int]]:
"""
x: 点坐标
y: 理想输出,+1 或 -1
lr: learning rate, 学习率
t: 参数优化次数
返回:训练完的参数,每次优化前误分类点的个数
"""
# 初始化参数
theta = np.zeros((len(x[0])+1, 1))
error_list = [] # 误分点列表
# 开始训练
for _ in range(t):
error_count = 0
error_index = []
for i, x_i in enumerate(x):
y_i = theta[0] * x_i[0] + theta[1] * x_i[1] + theta[2]
# 如果该点被分类错误
if y_i * y[i] <= 0:
error_index.append(i)
error_count += 1
# print(theta)
error_list.append(error_count)
# 随机选取一个误分类点进行参数优化
if error_count > 0:
i = random.choice(error_index)
theta[0] += lr * y[i] * x[i][0]
theta[1] += lr * y[i] * x[i][1]
theta[2] += lr * y[i] * 1
return theta, error_list
调用perceptron函数即可完成我们感知机的训练,得到一组合适的参数 θ \theta θ,我们可以将它转换为直线参数,转换公式如下:
- w e s t = − θ 0 / θ 1 w_{est} = - \theta_0 / \theta_1 west=−θ0/θ1
- b e s t = − θ 2 / θ 1 b_{est} = - \theta_2 / \theta_1 best=−θ2/θ1
并于我们的理想直线参数进行对比(如果样本点较少,可能与理想直线有较大差距。那是因为对于这个样本而言,分辨红蓝点的直线不唯一)。
然后我们再对数据进行可视化,代码如下:
# 根据数据集得到参数
theta, error_list = perceptron(sample_x, sample_y, 0.5, 100)
# 可视化
plt.rcParams['figure.figsize'] = (12.0, 4.0)
plt.subplot(121)
plt.xlim(xmax=-10, xmin=10)
plt.ylim(ymax=-10, ymin=10)
# plt.plot(x, y_ideal)
for i, p_x in enumerate(sample_x):
if sample_y[i] == 1:
plt.scatter(p_x[0], p_x[1], c='r', alpha=0.3)
else:
plt.scatter(p_x[0], p_x[1], c='b', alpha=0.3)
# 将 theta 转换为直线参数,绘制图像
w_est = - theta[0] / theta[1]
b_est = - theta[2] / theta[1]
print("the estimation of parameter are \n", w_est, "\n", b_est)
y_est = w_est * x + b_est
plt.plot(x, y_est, 'g', linewidth=10)
plt.subplot(122)
plt.plot(np.arange(len(error_list)), error_list, 'g+-')
plt.show()
得到下面这幅图
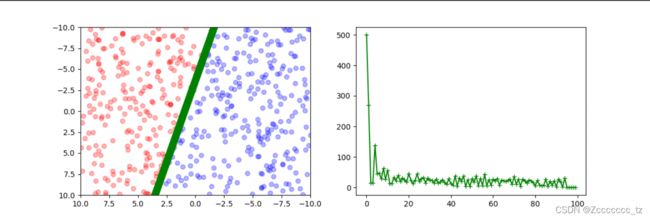
可以看到绿色的直线很好的将红蓝点分隔开来。
如果运行效果不好(指的是最后还有大量的点被误分),可以通过修改学习率以及优化次数来获得更准确的模型。
完整实验代码
import numpy as np
import matplotlib.pyplot as plt
import random
from typing import List, Tuple
def sample_point(w: float, b: float, num: int) -> Tuple[List[List[float]], List[float]]:
x, y = [], []
for _ in range(num):
p_x1 = np.random.random_sample(1) * 20 - 10
p_x2 = np.random.random_sample(1) * 20 - 10
p_y = 1 if w * p_x1 + b - p_x2 > 0 else -1
x.append([p_x1, p_x2])
y.append(p_y)
return x, y
def perceptron(x, y, lr, t) -> Tuple[np.ndarray, List[int]]:
theta = np.zeros((len(x[0])+1, 1))
error_list = [] # 误分点列表
# 开始训练
for _ in range(t):
error_count = 0
error_index = []
for i, x_i in enumerate(x):
y_i = theta[0] * x_i[0] + theta[1] * x_i[1] + theta[2]
# 如果该点被分类错误
if y_i * y[i] <= 0:
error_index.append(i)
error_count += 1
# print(theta)
error_list.append(error_count)
if error_count > 0:
i = random.choice(error_index)
theta[0] += lr * y[i] * x[i][0]
theta[1] += lr * y[i] * x[i][1]
theta[2] += lr * y[i]
return theta, error_list
def all_code():
# 生成散点图
w_ideal = np.random.random_sample(1) * 10 - 5
b_ideal = np.random.random_sample(1) * 10 - 5
print("the ideal parameter are \n", w_ideal, "\n", b_ideal)
x = np.linspace(-10, 10, 1000)
# line_ideal = w_ideal * x + b_ideal
# 搭建数据集
sample_x, sample_y = sample_point(w_ideal, b_ideal, 500)
# 根据数据集得到参数
theta, error_list = perceptron(sample_x, sample_y, 0.5, 100)
# 可视化
plt.rcParams['figure.figsize'] = (12.0, 4.0)
plt.subplot(121)
plt.xlim(xmax=-10, xmin=10)
plt.ylim(ymax=-10, ymin=10)
# plt.plot(x, y_ideal)
for i, p_x in enumerate(sample_x):
if sample_y[i] == 1:
plt.scatter(p_x[0], p_x[1], c='r', alpha=0.3)
else:
plt.scatter(p_x[0], p_x[1], c='b', alpha=0.3)
w_est = - theta[0] / theta[1]
b_est = - theta[2] / theta[1]
print("the estimation of parameter are \n", w_est, "\n", b_est)
y_est = w_est * x + b_est
plt.plot(x, y_est, 'g', linewidth=10)
plt.subplot(122)
plt.plot(np.arange(len(error_list)), error_list, 'g+-')
plt.show()
if __name__ == '__main__':
all_code()
参考资料
- 《统计学习方法》
- Implementing the Perceptron Algorithm in Python