Python实现感知机算法——李航《统计学习方法》

接下来一学期选了门《机器学习》的课程，所以打算把相关的作业也发上来！
一：
请说明感知机为何不能解决异或问题。
答：我们知道感知机属于线性模型，由于其无法找到一个线性模型对异或问题进行划分，所以其不能解决异或问题。具体解释如下：
首先我们知道感知机的数学表达式就是：
f(x)=sign(wx+b)
其中sign是符号函数，w和b都是感知机参数，x表示实例的特征向量，而y=f(x)就是实例的类别。以二维特征向量为例：
输入空间也就特征向量空间是 ，输出空间也是 ，输入 表示实例的特征向量，对于输入空间的点，输出 表示实例的类别。
由此知感知机为线性模型；
而对于异或问题，以二维为例：
输入 输出
Xi1 Xi2 Yi
0 0 0
1 0 1
0 1 1
1 1 0
利用Python绘制散点图如下

由上述知，异或问题输出可以分为两类，显示在二维坐标系中如上图所示：其中输出结果为1对应图中”o”，输出为0对应图中”x”，我们可以很容易发现对于这种情况无法找到一条直线将两类结果分开。所以感知机无法找到一个线性模型对异或问题进行划分。
实际上不单单是感知机无法处理异或问题，所有的线性模型都无法处理线性模型。
二、编程题：
请使用python构建一个感知机，对上述数据进行分类，并诚实滴给出分类准确率。
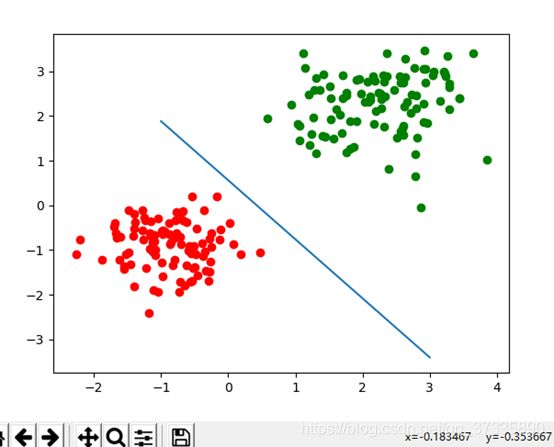
把分界面的表达式写于下方，并将其可视化出来粘贴到下方。
对于感知机Python代码，其内容如下，其主要步骤就是：
① 构建训练数据，形成适合训练的数据向量与标签向量
② 载入数据利用感知机数据进行计算得出感知机参数以获取感知机模型
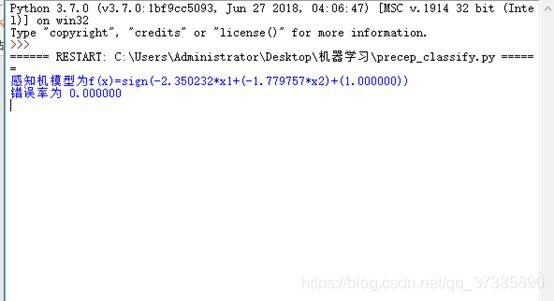
③ 将测试数据代入上述获取的感知机模型观察错误率结果（此处即将训练数据全部代入进行测试，获取的错误率为0）如下图所示，且感知机模型为
f(x)=sign(-2.350232x1+(-1.779757x2)+(1.000000))
注：由于选用的为高斯随机数据，故每次运行后参数有所不一样，但都能完全分类正确。。
④ 绘制相关图形界面



python代码如下：

import numpy as np
import matplotlib.pyplot as plt
num=100

# 类别 1 
class_1=np.random.normal(loc=2.3,scale=0.7,size=(num,2))
label_1=-1*np.ones((num,1))
classlabel_1=np.concatenate((class_1,label_1),axis=1)
#print(classlabel_1)
# 类别 2 
class_2=np.random.normal(loc=-0.9,scale=0.5,size=(num,2))
label_2=np.ones((num,1))
classlabel_2=np.concatenate((class_2,label_2),axis=1)

plt.figure()
plt.plot(class_1[:,0],class_1[:,1],"*")
plt.plot(class_2[:,0],class_2[:,1],"*")
#print(classlabel_2)
# 请根据课本构建数据标签 高斯分布 loc为均值 scale为标准差


#数据准备
classlabel=np.concatenate((classlabel_1,classlabel_2),axis=0)#拼接成一个整体
X1=classlabel[:,0]
X2=classlabel[:,1]
n=classlabel.shape[1]#训练数据特征数为n-1
Y=classlabel[:,2]    #构建标签数组
X=classlabel[:,0:n-1]#构建训练数据数组

#感知机分类学习
def precep_classify(data_mat, label_mat, eta=1):
    #eta为学习速率取1，omega为权重因子
    omega = np.mat(np.zeros(n-1))#omega为权重因子初值为0
    m = np.shape(data_mat)[0]    #获取总样本数
    b = 0                        #b为偏置初值为0
    error_data = True
    while error_data:
        error_data = False
        for i in range(m):
            judge = label_mat[i] * (np.dot(omega, data_mat[i].T)+b)
            if judge <= 0:       #判断y(wx+b)
                error_data = True
                omega = omega + np.dot(label_mat[i], data_mat[i])
                b=b+label_mat[i] #随机梯度下降法更新参数
    w_b=np.array([omega,b])
    return w_b                   #传回感知机参数

#可视化处理
def plot(data_mat, label_mat, omega, b):
    fig = plt.figure()
    ax = fig.add_subplot(111)
    X = data_mat[:, 0]
    Y = data_mat[:, 1]

    for i in range(len(label_mat)):
        if label_mat[i] > 0:
            ax.scatter(X[i].tolist(), Y[i].tolist(), color='red')
        else:
            ax.scatter(X[i].tolist(), Y[i].tolist(), color='green')
    o1 = omega[0, 0]
    o2 = omega[0, 1]
    x = np.linspace(-1, 3, 50)
    y = (-o1 * x - b) / o2
    ax.plot(x, y)
    plt.show()
#测试
def precep_test(test_data_mat, test_label_mat, omega, b):
    m = np.shape(test_data_mat)[0]
    error = 0.0
    for i in range(m):
        classify_num = np.dot(test_data_mat[i], omega.T)+b
        if classify_num > 0:
            class_ = 1
        else:
            class_ = -1
        if class_ != test_label_mat[i]:
            error += 1
    print ('错误率为 %f' %(error/m))
    

#主程序
for i in range(0,10):#多循环训练几次以提高抗噪容限
    w_b=precep_classify(X, Y)   #载入训练数据进行感知机分类获取参数

w=w_b[0]
b=w_b[1]
print("感知机模型为f(x)=sign(%f*x1+(%f*x2)+(%f))"%(w[0,0],w[0,1],b))
precep_test(X, Y, w, b)     #进行测试
plot(X, Y, w, b)            #可视化展示