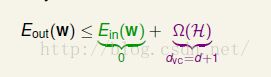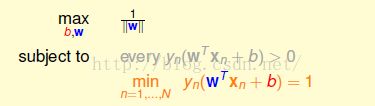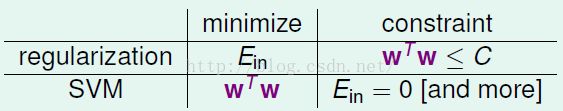机器学习技法(林軒田)笔记之一
Course Introduction
Course History
Course Design
在本课程中机器学习基石课程中所讲到的基本工具，将其延伸成复杂实用的模型。主要围绕特征转换的3个方向展开：
1.如果有很多特征转换要使用的时候如何应用特征转换，更重要的是这么多的特征转换可能会有复杂度的问题，我们怎么控制复杂度的问题，这样的想法刺激了SVM的发展；
2.我们能否找到一些具有预测性的特征，找出来之后能否将这些特征混合起来，让整个模型有更好的表现，这样的想法刺激了AdaBoost算法的发展；
3.如果资料中有隐藏的特征，那么机器怎样将这些特征学习出来让机器的想法更好，这样的想法刺激了早年的类神经网络的发展，近年来发展成为深度学习。
Large-Margin Separating Hyperplane
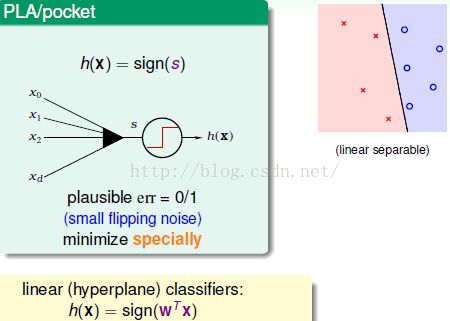
首先，我们回顾一下之前讲过的Linear Classfication ：有
和
，我们用一条直线将和分开，或者在高维空间中使用超平面将其分开。数学上，将资料拿来计算一个加权和，根据和的正负预测和。
现在，给定一个线性可分的资料，则会有很多条线将和分开，但是下图中的哪条线会更好呢？
PLA会选哪一条线与PLA看到的错误有关，因此PLA得到哪一条线不确定（PLA有一条线在手上，看到范一个错误就会转一下，范一个错误就转一下，最后会停在哪里跟看到错误的过程有关）。从之前的理论来看，三条线似乎也没什么区别，例如从VC Bound来看：
会被
和
之和所包围，其中为训练样本上的错误率，三条线都满足，为复杂度，都是线，因此复杂度都为d+1。但是我们的直觉告诉我们最右边是最好的线。
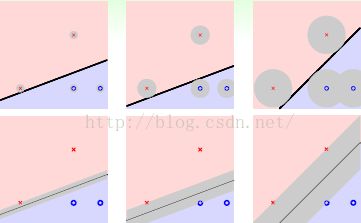
一种原始的简单解释：
假设我们已经拿到原始资料，即图上的点
，但是在测试的时候我们拿到跟原始资料相近的资料(测量误差、资料收集等造成)，下图中灰色的x。所以，测试资料可能会和训练资料有点出入。
假设我们绝对相信我们的训练资料，如果有误差，则我们人为最好的预测为将测试资料预测的与训练资料很接近(不完全一样)。
上图中左边与右边最大的差别就在于对测量误差的容忍度，点距离线越远则容忍度越好，进而可以避免过拟合：
如果数据有一些误差的话，最有更有可能容忍。换个角度，如果从线离点有多远，就是从线有多胖的角度来看。
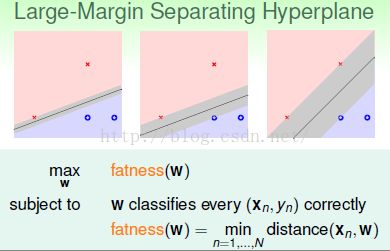
定义：
我们要找出一条线，首先这条线可以将和分开(线性可分)，然后取最胖的一条线，即计算所有点到线的距离，取其中最小的距离。线有多胖，就看它离最接近的短的距离。
问题就可以变成一下这个简单的最佳化问题：
找出一条线，满足两条特性，1·把点分开 2·选一条最胖的线 定义线的胖就是线离所有点的距离中的最小值。
进而：
其中：
胖表示边界margin并且资料线性可分即上面的correctness部分。
Standard Large-Margin Problem
由上节课中我们知道，在上述最佳化问题中，我们需要求解点到线的距离，所以我们这节首先讨论如何计算距离：
之前我们将x加一个
，并且w加一个
。但是，我们发现在计算距离的时候这样做不是很方便，因此我们将其与w分开，将作为b(截距bias)，因此也不需要。
我们的目标就是一个平面到点x的距离是多少：
我们考虑平面上的两个点，则：
由上图可以得出w为平面的法向量，则点到平面的距离为平面外一点与平面内一点的连线在法向量上的投影，即：
我们考虑的是线性可分问题，因此：会有如下性质即算出来的分数和我们的分类结果是同号的，如下，进而可以将绝对值符号去掉。
进而：
进一步简化，其实世上可能没有那么多条线，例如，平面上的线可以用不同的方式表达，即线的系数可以放缩表示同一条线，因此我们用一些特别的放缩使得式子更简单：就是将其放缩至1
进而最优化问题变成如下所示，加了一个限制条件，要求希望最小的等于1，直接覆盖了其上面的灰色限制条件：
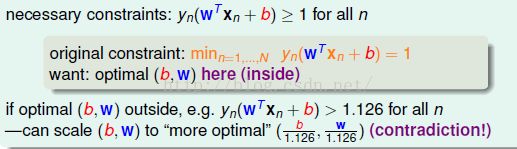
进一步，我们将限制条件放宽看是否好解，但是得证明，将条件放松不会影响解的范围。如果最小的一个等于1，则所有的必须满足大于等于1.我们希望最终接仍落在原来的等于1的范围内。假设最优解让其值统统大于1如1.126，没有等于1，我们就可以让b,w放缩都除以1.126，则最终仍会满足大于等于1，可是要求的w就变短了，结果求的max就会变大，比原来的解更好，这就矛盾了。这就代表如果b,w落在外面的区域，就不会是最佳解。所以就可以轻易放松条件，而不影响最优解。
例如，b,w在范围外，则w会变小进而距离会变大即与距离最大矛盾，因此条件放宽，b,w范围不变。
将最大化问题转化为最小化问题：
上节中我们得到的式子我们称之为标准的问题：
下面我们通过一个特殊的例子来探讨这个问题的解法：
给出四个点，坐标如下，一个点得到一个条件，最终得到四个条件。
进而：
支持向量机的解释：如上图，当我们找到最胖的线(平面)后，会有一些离其最近的点，并且将其它点忽略掉。因此我们可以将点分为两类，一类告诉我们最胖的线的位置，一类没有告诉我们任何事情。其中告诉我们最胖的线的位置，离边界最近的点我们称之为支持向量(实质上只是候选人，后面具体介绍)。
支持向量：
找到边界上的支持向量，即可找到最胖的边界在那。
下面介绍复杂的问题的解法：
分析可知，上式是一个二次规划问题（线性规划的进阶版）
下面将我们的问题表示成标准的二次规划问题：
最小化一个关于u向量的二次函数，将系数放在一个Q矩阵里面，可能会有一次项，我们把它放在p向量里面。条件都是线性的，可能有很多条件，条件中的系数放在am里面，常数放在cm里面。
二次规划问题一般是最小化关于一个向量u的二次函数，Q为二次式的系数矩阵，一次项放在p向量中，条件都是现行的，即是u向量的一次式，系数放在
中，条件放在
中。
进而 确定Q时，因为不在乎b向量，所以会有三部分为0，还有一部分是I单位矩阵，表示产生联系。p为0不需要一次项：
总结：硬边界SVM求解步骤：
其中，Hard Margin是指和必须完全分开，linear是指使用原来的
。
非线性的将x做一个转换就行：
Reasons behind Large-Margin Hyperplane
在上节课所讲述的标准SVM的基础上，如果我们想要进行非线性分类，将x转换成z即可：
现在我们介绍保证SVM能够得到较好的分类的理论原因、解释：
以前讲regularization的时候我们希望
越小越好，为避免过拟合我们加上了长度限制；
在SVM中我们最小化的是w的长度，但是加了更多的约束条件。
另外一种解释：
在VC维中我们探讨的是线可以有多少种方法将圈圈和叉叉分成不同的排列组合，如果现在我们找的是胖的线，如果找不到一条胖的线，那么我们也可以分析这种算法的VC维，即在某组特定的数据集上到底可以找出多少种圈圈叉叉的排列组合。
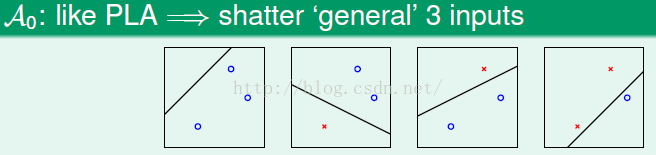
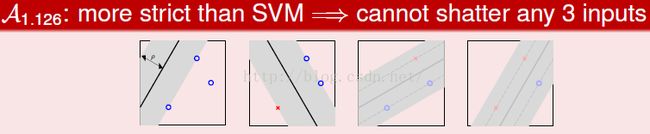
如果不计较胖瘦，例如PLA：
三个点的时候，所有的排列组合都可以分出来。
计较胖瘦，例如SVM
则可能做不出所有的排列组合。
得出：
大边界算法的VC维：
与数据集有关，
与数据集无关。
概念：算法最多可以最多shatter(产生所有的圈圈叉叉的排列组合)多少个点。
计算方法：
如果不考虑胖瘦，则圆上的三个点可以被完全shatter，即
；
如果考虑胖瘦，则
。
证明得到：
大边界超平面的优点：
