VAE变分自编码器

变分自编码器学习记录（VAE）

参考链接

理论讲解参考

公式推导参考

代码参考

一、变分自编码器简述

Variational Autoencoder(VAE)作为一类深度生成模型，是由 Kingma 等人于 2014 年提出的基于变分贝叶斯（Variational Bayes，VB）推断的生成式网络结构。与传统的自编码器通过数值的方式描述潜在空间不同，它以概率的方式描述对潜在空间的观察，在数据生成方面表现出了巨大的应用价值。是无监督学习领域的重要研究课题。

原论文的链接：https://arxiv.org/abs/1312.6114

二、理论推导

2.1 VAE概述

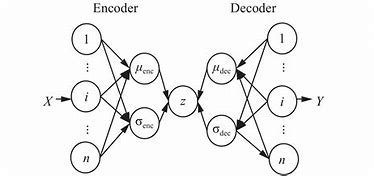
变分自编码器（VAE）与自编码器（AE）分为编码器(encoder)和解码器(decoder)的结构类似。VAE利用两个神经网络建立两个概率密度分布模型：一个用于原始输入数据的变分推断，生成隐变量的变分概率分布，称为推断网络；另一个根据生成的隐变量变分概率分布，还原生成原始数据的近似概率分布，称为生成网络。

通过推断网络，将数据映射到一个隐变量层，可以把隐层看成是一种数据降维或者特征提取的过程。在一些教程中讲到隐变量具有特定的含义，比如在手写数字集表示所写的数字几，我认为这些隐变量仅仅表示高维特征的降维，而不见得具有实际的意义，并且对隐变量的解释也是一个值得研究的问题。

2.2 理论推导

推断网络的生成过程：$q_{\Phi }(z|x)=N(\mu (x;\Phi ),{\sigma }^2(x;\Phi ))$

生成网络的生成过程：$p_{\theta }(x|z)=N(\mu (z;\theta ),{\sigma }^2(z;\theta ))$

能够看到推断网络和生成函数均是高斯分布，可以将推断网络和生成网络的过程看成一种复杂的映射关系，由于使用神经网络实现这种映射，因此对随机变量分布做出的这种假设能够通过神经网络的强大拟合能力得到合适的参数。均值$\mu$和方差${\sigma }^2$都是函数，其参数$\theta$,$\Phi$由模型训练过程中得到。

下面对结果做推导，不感兴趣的同学可以直接看最后的结果和代码实现。

令 $$\begin{gathered} L=log(p(x)) \\ =\int q\left(z\right)\log \left(p\left(x;\theta \right)\right)dz \\ =\int \begin{array}{c}q\left(z\right)\log \left(\frac{p\left(z,x;\theta \right)}{p\left(z|x;\theta \right)}\right)\end{array}dz \\ =\int \begin{array}{c}q\left(z\right)\log \left(\frac{p\left(z,x;\theta \right)q\left(z\right)}{q\left(z\right)p\left(z|x;\theta \right)}\right)\end{array}dz \\ =\int \begin{array}{c}q\left(z\right)\log \left(\frac{p\left(z,x;\theta \right)}{q\left(z\right)}\right)\end{array}dz+\int q\left(z\right)\log \left(\frac{q\left(z\right)}{p\left(z|x;\theta \right)}\right)dz \end{gathered}$$

这里可以把$q(z)$看作是$z$的概率密度函数，满足$\int q(z)=1$。但是该分布很难求解，变分法就是将这个概率分布转化为$x$生成$z$的条件概率$q_{\Phi }(z|x)$对分布进行近似。

即
$$\begin{gathered} L=\int q_{\Phi }(z|x)\log \left(\frac{p\left(z,x;\theta \right)}{q_{\Phi }(z|x)}\right)dz+\int q_{\Phi }(z|x)\log \left(\frac{q_{\Phi }(z|x)}{p\left(z|x;\theta \right)}\right)dz \\ =L^v+D_{KL}(q_{\Phi }(z|x)||p(z|x;\theta )) \end{gathered}$$

$x$的概率密度$p(x)$是给定的，所以$L$是一个确定的值，可以看到该式各项在VAE中具有实际意义。VAE推断网络的目的是尽可能使$q_{\Phi }(z|x)$逼近$p(z|x;\theta )$，也就是最小化KL散度项。这里引入了变分下限的概念，由于KL散度恒大于0，所以$L⩾L^v$。最小化KL散度的目标就等价为最大化变分下限。

$$\begin{gathered} L^v=\int q_{\Phi }\left(z|x\right)\log \left(\frac{p_{\theta }\left(z,x\right)}{q_{\Phi }\left(z|x\right)}\right)dz \\ =\int q_{\Phi }\left(z|x\right)\log \left(\frac{p_{\theta }\left(x|z\right)p_{\theta }\left(z\right)}{q_{\Phi }\left(z|x\right)}\right)dz \\ =\int q_{\Phi }\left(z|x\right)\log \left(p_{\theta }(x|z)\right)dz+\int q_{\Phi }\left(z|x\right)\log \left(\frac{p_{\theta }\left(z\right)}{q_{\Phi }\left(z|x\right)}\right)dz \\ =-D_{KL}\left(q_{\Phi }\left(z|x\right)||p_{\theta }\left(z\right)\right)+\int q_{\Phi }\left(z|x\right)\log \left(p_{\theta }(x|z)\right)dz \end{gathered}$$

原式转换为最小化$D_{KL}\left(q_{\Phi }\left(z|x\right)||p_{\theta }\left(z\right)\right)$，最大化$\int q_{\Phi }\left(z|x\right)\log \left(q_{\Phi }\left(z|x\right)\right)dz$

记
$$\begin{gathered} L_1=-D_{KL}\left(q_{\Phi }\left(z|x\right)||p_{\theta }\left(z\right)\right) \\ =\int q_{\Phi }\left(z|x\right)\log \left(p_{\theta }\left(z\right)\right)dz-\int q_{\Phi }\left(z|x\right)\log \left(q_{\Phi }\left(z|x\right)\right)dz \end{gathered}$$

其中$L_1$第一项：

$$\begin{gathered} \int q_{\Phi }(z|x)log(p_{\theta }(z))dz \\ =\int N(\mu (x;\Phi ),{\sigma }^2(x;\Phi ))log(N(z;0,1))dz \\ =E_{zN(\mu ,{\sigma }^2)}[log(N(Z;0,1))] \\ =E_{zN(\mu ,{\sigma }^2)}[log(\frac{1}{\sqrt{2\pi }}{e}^{-\frac{z^2}{2}})] \\ =-\frac{1}{2}log(2\pi )-\frac{1}{2}{E}_{zN(\mu ,{\sigma }^2)}[z^2] \\ =-\frac{1}{2}log(2\pi )-\frac{1}{2}({\mu }^2+{\sigma }^2) \end{gathered}$$

$L_1$第二项：

$$\begin{gathered} \int q_{\Phi }(z|x)log(q_{\Phi }(z|x))dz \\ =\int N(\mu (x;\Phi ),{\sigma }^2(x;\Phi ))log(N(\mu (x;\Phi ),{\sigma }^2(x;\Phi )))dz \\ =E_{zN(\mu ,{\sigma }^2)}[log(N(\mu (x;\Phi ),{\sigma }^2(x;\Phi ))))] \\ =E_{zN(\mu ,{\sigma }^2)}[log(\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{(z-\mu {)}^2}{2}})] \\ =-\frac{1}{2}log(2\pi )-\frac{1}{2}log({\sigma }^2)-\frac{1}{2}{E}_{zN(\mu ,{\sigma }^2)}[(z-\mu {)}^2] \\ =-\frac{1}{2}log(2\pi )-\frac{1}{2}(log({\sigma }^2)+1) \end{gathered}$$

综上：

$$\begin{gathered} L_1=-\frac{1}{2}({\mu }^2+{\sigma }^2)+\frac{1}{2}(log({\sigma }^2)+1) \\ =\frac{1}{2}(log({\sigma }^2)+1-{\mu }^2-{\sigma }^2) \end{gathered}$$

记
$$L_2=\int q_{\Phi }\left(z|x\right)\log \left(p_{\theta }(x|z)\right)dz$$

$q$的分布为：$q_{\Phi }(z|x)=N(\mu (x;\Phi ),{\sigma }^2(x;\Phi ))$

$p$的分布为：$p_{\theta }(x|z)=N(\mu (z;\theta ),{\sigma }^2(z;\theta ))$

直接计算不容易得到，这里使用MC方法（蒙特卡洛方法）,采样得到如下近似结果。

$$L_2=\frac{1}{L}\sum _{l=1}^L\log \left(p_{\theta }\left(x^{\left(i\right)}|z^{\left(i,l\right)}\right)\right)$$

其中$z^{(i,l)}={\mu }^{(i)}+{\sigma }^{(i)}\odot {ϵ}^{(l)},{ϵ}^{(l)}\sim N(0,1)$

这里$i$是$x$不同特征的索引，$l$表示不同的采样点，通过采样$z$在参数$\theta$下生成新的$x$。$\mu$和$\sigma$是由参数$\Phi$确定的，因此$L_2$是关于参数$\theta$和$\Phi$的函数。

综合上述的所有推导，利用神经网络优化的目标为：

$$L^v=\frac{1}{2}(log({\sigma }^2)+1-{\mu }^2-{\sigma }^2)+\frac{1}{L}\sum _{l=1}^L\log \left(p_{\theta }\left(x^{\left(i\right)}|z^{\left(i,l\right)}\right)\right)$$

该式的两项在VAE中具有实际意义，第一项表示正则项，最大化使得$z$尽可能符合先验，第二项表示重建项。在实现过程中损失函数要最小化，因此损失函数为：

$$Loss=\frac{1}{2}(log({\sigma }^2)+1-{\mu }^2-{\sigma }^2)-\frac{1}{L}\sum _{l=1}^L\log \left(p_{\theta }\left(x^{\left(i\right)}|z^{\left(i,l\right)}\right)\right)$$

边际概率根据变量的形式不同采用不同的概率表达式。二进制变量使用伯努利分布，连续分布变量使用高斯分布。详细的实现过程可以借助代码理解。

三、代码实现

代码参考 https://www.cnblogs.com/picassooo/p/12601785.html

import os
import torch
import torch.nn.functional as F
from torch import nn
from torch.utils.data import DataLoader
from torchvision.datasets import MNIST
from torchvision import transforms as tfs
from torchvision.utils import save_image

# Hyper parameters
EPOCH = 1
LR = 1e-3
BATCHSIZE = 128

im_tfs = tfs.Compose([
    tfs.ToTensor(),    # Converts a PIL.Image or numpy.ndarray to
                       # torch.FloatTensor of shape (C x H x W)
])

# dataset
train_set = MNIST(
    root=r"Your path",  # you should use your path
    download=False,   # mnist has been downloaded before, use it directly
    train=True,
    transform=im_tfs,
)
train_loader = DataLoader(train_set, batch_size=BATCHSIZE, shuffle=True)

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()
 
        self.fc1 = nn.Linear(784, 400)
        self.fc21 = nn.Linear(400, 20)   # mean
        self.fc22 = nn.Linear(400, 20)   # var
        self.fc3 = nn.Linear(20, 400)
        self.fc4 = nn.Linear(400, 784)
 
    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)
 
    def reparametrize(self, mu, logvar):
        std = logvar.mul(0.5).exp_()                  
        eps = torch.FloatTensor(std.size()).normal_()    
        if torch.cuda.is_available():
            eps = eps.cuda()
        return eps.mul(std).add_(mu) 
 
    def decode(self, z):
        h3 = F.relu(self.fc3(z))
        return torch.sigmoid(self.fc4(h3))
 
    def forward(self, x):
        mu, logvar = self.encode(x)          
        z = self.reparametrize(mu, logvar)   
        return self.decode(z), mu, logvar    

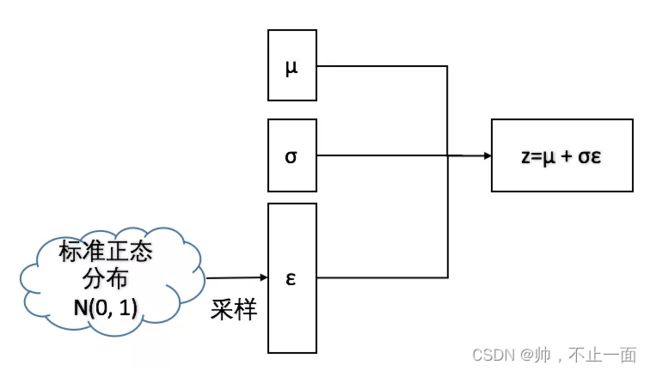
在核心代码部分，可以看到作者提出的重参数化方法。原本随机采样会带来无法反向传播求解梯度的问题。作者使用重参数化解决了该问题，把直接采样转化为标准正态分布采样之后乘方差加均值。与直接采样的结果等价，但是可以应用反向传播算法优化参数。

reconstruction_function = nn.MSELoss(reduction='sum')

def loss_function(recon_x, x, mu, logvar):
    """
    recon_x: generating images
    x: origin images
    mu: latent mean
    logvar: latent log variance
    """
    # MLD: marginal likelihood
    MLD=-torch.sum(x.view(-1,784)*torch.log(recon_x.view(-1,784))+(1-x.view(-1,784))*torch.log(1-recon_x.view(-1,784)))  
    # KLD divergence
    KLD_element = mu.pow(2).add_(logvar.exp()).mul_(-1).add_(1).add_(logvar)
    KLD = torch.sum(KLD_element).mul_(-0.5)  # KL divergence
    return MLD + KLD

def to_img(x):   # x shape (bachsize, 28*28), x pixel_range[-1., 1.]
    '''
    reshape the result to img
    '''
    x = 0.5 * (x + 1.)
    x = x.clamp(0, 1)
    x = x.view(x.shape[0], 1, 28, 28)
    return x

# train
for epoch in range(EPOCH):
    for iteration, (im, y) in enumerate(train_loader):
        im = im.view(im.shape[0], -1)
        if torch.cuda.is_available():
            im = im.cuda()
        recon_im, mu, logvar = net(im)
        loss = loss_function(recon_im, im, mu, logvar) / im.shape[0]   # mean of loss
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
 
        if iteration % 100 == 0:
            print('epoch: {:2d} | iteration: {:4d} | Loss: {:.4f}'.format(epoch, iteration, loss.data.numpy()))
            save = to_img(recon_im.cpu().data)
            if not os.path.exists('./vae_img'):
                os.mkdir('./vae_img')
            save_image(save, './vae_img/image_{}_{}.png'.format(epoch, iteration))

训练的结果：

# test
code = torch.randn(1, 20)   # randn tensor as test input
out = net.decode(code)
img = to_img(out)
save_image(img, './vae_img/test_img.png')

结果使用随机向量生成，测试效果不佳。

四、后记

由于笔者能力有限，对于很多问题的理解不够深入，尤其对于变分法方面没有深刻的认识，如果希望更多的理解，还请参考原文章。
本文主要综合上面提到的几篇博客以及作者的原文写成，一些公式推导是结合老师上课讲解的内容，主要作为学习记录之用。如有谬误，还请指出。