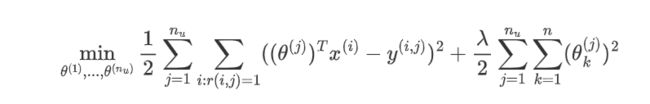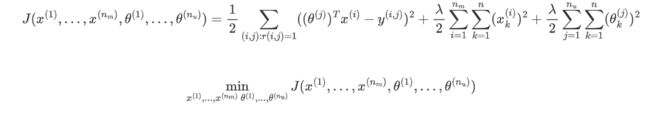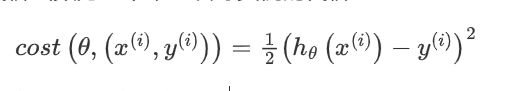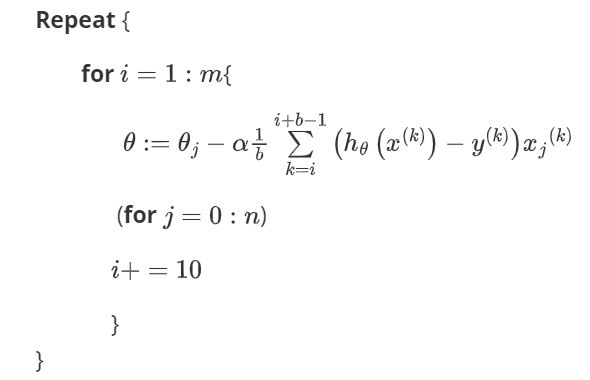机器学习—吴恩达_ 第12周_学习总结
机器学习—吴恩达_ 第12周_学习总结
21.11.22-21.11.28
推荐系统
协同过滤Collaborative filtering, CF
CF有两种基本方法:基于用户的协同过滤和基于项目的协同过滤。 步骤:
- 了解数据库中有多少用户/项目与给定的用户/项目相似。
- 考虑到与它类似的用户/项目的总权重,评估其他用户/项目,来预测你会给该产品用户的打分。
在协同过滤从算法中,通常不使用方差项,算法会自动学得。
协同过滤优化目标:
- 给定 x ( 1 ) , . . . , x ( n m ) x^{(1)},...,x^{(n_m)} x(1),...,x(nm),估计 θ ( 1 ) , . . . , θ ( n u ) \theta^{(1)},...,\theta^{(n_u)} θ(1),...,θ(nu):
-
给定 θ ( 1 ) , . . . , θ ( n u ) \theta^{(1)},...,\theta^{(n_u)} θ(1),...,θ(nu),估计 x ( 1 ) , . . . , x ( n m ) x^{(1)},...,x^{(n_m)} x(1),...,x(nm):同时最小化 x ( 1 ) , . . . , x ( n m ) x^{(1)},...,x^{(n_m)} x(1),...,x(nm)和 θ ( 1 ) , . . . , θ ( n u ) \theta^{(1)},...,\theta^{(n_u)} θ(1),...,θ(nu):
协同过滤算法使用步骤如下:
-
初始 x ( 1 ) , x ( 1 ) , . . . x ( n m ) , θ ( 1 ) , θ ( 2 ) , . . . , θ ( n u ) x^{(1)},x^{(1)},...x^{(nm)},\ \theta^{(1)},\theta^{(2)},...,\theta^{(n_u)} x(1),x(1),...x(nm), θ(1),θ(2),...,θ(nu)为一些随机小值
-
使用梯度下降算法最小化代价函数
-
在训练完算法后,我们预测 ( θ ( j ) ) T x ( i ) (\theta^{(j)})^Tx^{(i)} (θ(j))Tx(i)为用户 j j j 给电影 i i i 的评分
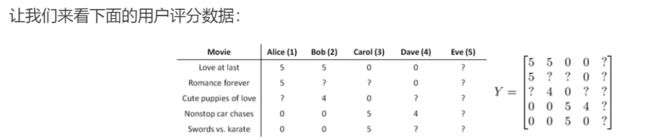
通过这个学习过程获得的特征矩阵包含了有关电影的重要数据,这些数据不总是人能读懂的,但是我们可以用这些数据作为给用户推荐电影的依据。
例如,如果一位用户正在观看电影 x ( i ) x^{(i)} x(i),我们通过两部电影的特征向量之间的距离 ∥ x ( i ) − x ( j ) ∥ \left\| {{x}^{(i)}}-{{x}^{(j)}} \right\| ∥∥x(i)−x(j)∥∥的大小可以寻找另一部电影 x ( j ) x^{(j)} x(j)。
低秩矩阵分解
均值归一化
大规模学习
大型数据集的学习
如果我们有一个低方差的模型,增加数据集的规模可以获得更好的结果。我们应该怎样应对一个有100万条记录的训练集?
以线性回归模型为例,每一次梯度下降迭代,我们都需要计算训练集的误差的平方和,如果我们的学习算法需要有20次迭代,这便已经是非常大的计算代价。
首先应该做的事是去检查一个这么大规模的训练集是否真的必要,也许只用1000个训练集也能获得较好的效果,同时可以绘制学习曲线来帮助判断。
随机梯度下降法
如果一定需要一个大规模的训练集,可以使用随机梯度下降法来代替批量梯度下降法。
在随机梯度下降法中,定义代价函数为一个单一训练实例的代价
随机梯度下降算法在每一次计算之后便更新参数 θ {{\theta }} θ ,而不需要首先将所有的训练集求和,在梯度下降算法还没有完成一次迭代时,随机梯度下降算法便已经走出了很远。但是这样的算法存在的问题是,不是每一步都是朝着”正确”的方向迈出的。因此算法虽然会逐渐走向全局最小值的位置,但是可能无法站到那个最小值的那一点,而是在最小值点附近徘徊。
小批量梯度下降
小批量梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法,每计算常数 b b b次训练实例,便更新一次参数 θ {{\theta }} θ 。
令 b b b 在 2-100 之间。这样做的好处在于可以用向量化的方式来循环 b b b个训练实例,如果我们用的线性代数函数库比较好,能够支持并行处理,那么算法的总体表现将不受影响(与随机梯度下降相同)。
随机梯度下降收敛
在批量梯度下降中,我们可以令代价函数 J J J为迭代次数的函数,绘制图表,根据图表来判断梯度下降是否收敛。但是,在大规模的训练集的情况下,这是不现实的,因为计算代价太大了。
每一次更新 θ {{\theta }} θ 之前都计算一次代价,然后每 x x x次迭代后,求出这 x x x次对训练实例计算代价的平均值,然后绘制这些平均值与 x x x次迭代的次数之间的函数图表。
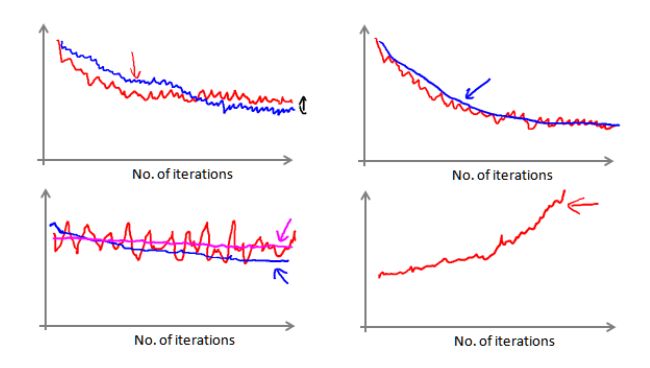
当我们绘制这样的图表时,可能会得到一个颠簸不平但是不会明显减少的函数图像(如上面左下图中蓝线所示)。我们可以增加 α α α来使得函数更加平缓,能看出下降的趋势(如上面左下图中红线所示);或者可能函数图表仍然是颠簸不平且不下降的(如洋红色线所示),那么我们的模型本身可能存在一些错误。
如果我们得到的曲线如上面右下方所示,不断地上升,那么可能会需要选择一个较小的学习率 α α α。
在线学习
如果有一个由连续的用户流引发的连续的数据流,进入你的网站,我们可以使用一个在线学习机制,从数据流中学习用户的偏好,然后使用这些信息来优化一些关于网站的决策。
一个算法来从中学习的时候来模型化问题在线学习算法指的是对数据流而非离线的静态数据集的学习。许多在线网站都有持续不断的用户流,对于每一个用户,网站希望能在不将数据存储到数据库中便顺利地进行算法学习。
一旦对一个数据的学习完成了,我们便可以丢弃该数据,不需要再存储它了。这种方式的好处在于,我们的算法可以很好的适应用户的倾向性,算法可以针对用户的当前行为不断地更新模型以适应该用户。
我们所使用的这个算法与随机梯度下降算法非常类似,唯一的区别的是,我们不会使用一个固定的数据集,我们会做的是获取一个用户样本,从那个样本中学习,然后丢弃那个样本并继续下去,在线学习的一个优点就是,如果有一个变化的用户群,在尝试预测的事情,在缓慢变化,就像你的用户的品味在缓慢变化,这个在线学习算法,可以慢慢地调试你所学习到的假设,将其调节更新到最新的用户行为
映射化简和数据并行
映射化简和数据并行对于大规模机器学习问题而言是非常重要的概念。之前提到,如果我们用批量梯度下降算法来求解大规模数据集的最优解,我们需要对整个训练集进行循环,计算偏导数和代价,再求和,计算代价非常大。如果我们能够将我们的数据集分配给不多台计算机,让每一台计算机处理数据集的一个子集,然后我们将计所的结果汇总在求和。这样的方法叫做映射简化。
案例
滑动窗口
滑动窗口是一项用来从图像中抽取对象的技术。假使我们需要在一张图片中识别行人,首先要做的是用许多固定尺寸的图片来训练一个能够准确识别行人的模型。然后我们用之前训练识别行人的模型时所采用的图片尺寸在我们要进行行人识别的图片上进行剪裁,然后将剪裁得到的切片交给模型,让模型判断是否为行人,然后在图片上滑动剪裁区域重新进行剪裁,将新剪裁的切片也交给模型进行判断,如此循环直至将图片全部检测完。一旦完成后,我们按比例放大剪裁的区域,再以新的尺寸对图片进行剪裁,将新剪裁的切片按比例缩小至模型所采纳的尺寸,交给模型进行判断,如此循环。
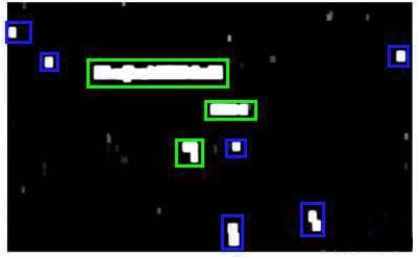
滑动窗口技术也被用于文字识别,首先训练模型能够区分字符与非字符,然后,运用滑动窗口技术识别字符,一旦完成了字符的识别,我们将识别得出的区域进行一些扩展,然后将重叠的区域进行合并。接着我们以宽高比作为过滤条件,过滤掉高度比宽度更大的区域(认为单词的长度通常比高度要大)。下图中绿色的区域是经过这些步骤后被认为是文字的区域,而红色的区域是被忽略的。
获取大量数据和人工数据
以我们的文字识别应用为例,我们可以字体网站下载各种字体,然后利用这些不同的字体配上各种不同的随机背景图片创造出一些用于训练的实例,这让我们能够获得一个无限大的训练集。这是从零开始创造实例。
另一种方法是,利用已有的数据,然后对其进行修改,例如将已有的字符图片进行一些扭曲、旋转、模糊处理。只要我们认为实际数据有可能和经过这样处理后的数据类似,我们便可以用这样的方法来创造大量的数据。
有关获得更多数据的几种方法:
1. 人工数据合成
2. 手动收集、标记数据
3. 众包