详解机器学习损失函数之交叉熵

本文始发于个人公众号：TechFlow，原创不易，求个关注

今天这篇文章和大家聊聊机器学习领域的熵。

我在看paper的时候发现对于交叉熵的理解又有些遗忘，复习了一下之后，又有了一些新的认识。故写下本文和大家分享。

熵这个概念应用非常广泛，我个人认为比较经典的一个应用是在热力学当中，反应一个系统的混乱程度。根据热力学第二定律，一个孤立系统的熵不会减少。比如一盒乒乓球，如果把盒子掀翻了，乒乓球散出来，它的熵增加了。如果要将熵减小，那么必须要对这个系统做功，也就是说需要有外力来将散落的乒乓球放回盒子里，否则乒乓球的分布只会越来越散乱。

开创了信息论的香农大佬灵光一闪，既然自然界微观宏观的问题都有熵，那么信息应该也有。于是他开创性地将熵这个概念引入信息论领域，和热力学的概念类似，信息论当中的熵指的是信息量的混乱程度，也可以理解成信息量的大小。

信息量

举个简单的例子，以下两个句子，哪一个句子的信息量更大呢？

1. 我今天没中彩票
2. 我今天中彩票了

从文本上来看，这两句话的字数一致，描述的事件也基本一致，但是显然第二句话的信息量要比第一句大得多，原因也很简单，因为中彩票的概率要比不中彩票低得多。

相信大家也都明白了，一个信息传递的事件发生的概率越低，它的信息量越大。我们用对数函数来量化一个事件的信息量：

$$I(X)=-log(P(X))$$

因为一个事件发生的概率取值范围在0到1之间，所以log(p(X))的范围是负无穷到0，我们加一个负号将它变成正值。画成函数大概是下面这个样子：

信息熵

我们上面的公式定义的是信息量，但是这里有一个问题，我们定义的只是事件X的一种结果的信息量。对于一个事件来说，它可能的结果可能不止一种。我们希望定义整个事件的信息量，其实也很好办，我们算下整个事件信息量的期望即可，这个期望就是信息熵。

期望的公式我们应该都还记得：

$$E(X)=\sum P(X)X$$

我们套入信息量的公式可以得到信息熵H(x)：

$$H(X)=-\sum _{i=1}^{n}P(x_i)log(P(x_i))$$

相对熵（KL散度）

在我们介绍相对熵之前，我们先试着思考一个问题，我们为什么需要相对熵这么一个概念呢？

原因很简单，因为我们希望测量我们训练出来的模型和实际数据的差别，相对熵的目的就是为了评估和验证模型学习的效果。也就是说相对熵是用来衡量两个概率分布的差值的，我们用这个差值来衡量模型预测结果与真实数据的差距。明白了这点之后，我们来看相对熵的定义：

$$D_{KL}(P||Q)=\sum _{i=1}^{n}P(x_i)log(\frac{P(x_i)}{Q(x_i)})$$

如果把${\sum }_{i=1}^n{x}_i$看成是一个事件的所有结果，那$x_i$可以理解成一个事件的一个结果。那么所有的$P(x_i)$和$Q(x_i)$就可以看成是两个关于事件X的概率分布。$P(x_i)$样本真实的分布，我们可以求到。而$Q(x_i)$是我们模型产出的分布。KL散度越小，表示这两个分布越接近，说明模型的效果越好。

光看上面的KL散度公式可能会云里雾里，不明白为什么能反应P和Q两个分布的相似度。因为这个公式少了两个限制条件：

$$\sum _{i=1}^{n}P(x_i)=1,\sum _{i=1}^{n}Q(x_i)=1$$

对于单个$P(x_i)$来说，当然$Q(x_i)$越大$P(x_i)log(\frac{P(x_i)}{Q(x_i)})$越小。但由于所有的$Q(x_i)$的和是1，当前的i取的值大了，其他的i取的值就要小。

我们先来直观地感受一下，再来证明。

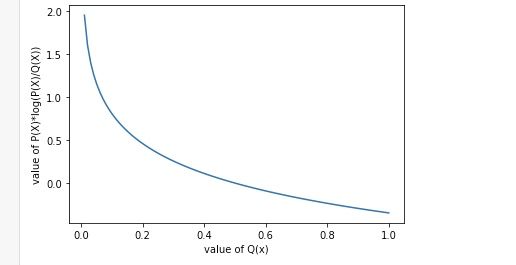
我们假设$x_i$只有0和1两个取值，也就是一个事件只有发生或者不发生。我们再假设$P(x=0)=P(x=1)=0.5$，我们画一下$P(x_i)log(\frac{P(x_i)}{Q(x_i)})$的图像：

和我们预料的一样，函数随着$Q(x_i)$的递增而递减。但是这只是一个x的取值，别忘了，我们相对熵计算的是整个分布，那我们加上另一个x的取值会发生什么呢？

从函数图像上，我们很容易看出，当Q(x)=0.5的时候，KL散度取最小值，最小值为0。我们对上面的公式做一个变形：

$$D_{KL}(P||Q)=\sum _{i=1}^{n}P(x_i)log(\frac{P(x_i)}{Q(x_i)})=\sum _{i=1}^{n}P(x_i)log(P(x_i))-\sum _{i=1}^{n}P(x_i)log(Q(x_i))$$

这个式子左边${\sum }_{i=1}^{n}P(x_i)log(P(x_i))$其实就是$-H(X)$，对于一个确定的事件X来说，它的信息熵是确定的，也就是说$H(X)$是一个常数，$P(x_i)$也是常数。log函数是一个凹函数，-log是凸函数。我们把$P(x_i)$当成常数的话，可以看出$-{\sum }_{i=1}^{n}P(x_i)log(Q(x_i))$是一个凸函数。

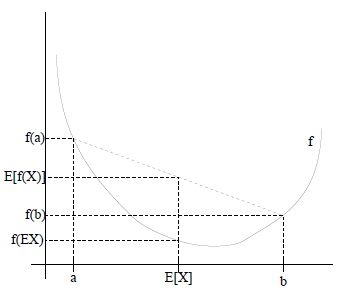
凸函数有一个jensen不等式：$f(E(X))\ge E(f(X)$，也即：变量期望的函数值大于变量函数值的期望，有点绕口令，看不明白没关系，可以通过下图直观感受：

我们利用这个不等式试着证明：$D_{KL}\ge 0$

首先，我们对原式进行变形：

$$D_{KL}=\sum _{i=1}^{n}P(x_i)log(\frac{P(x_i)}{Q(x_i)})=E(log(\frac{P(x_i)}{Q(x_i)}))=E[-log(\frac{Q(x_i)}{P(x_i)})]$$

然后我们利用不等式：

$$E[-log(\frac{Q(x_i)}{P(x_i)})]\ge -log(E[\frac{Q(x_i)}{P(x_i)}])=-log(\sum _{i=1}^{n}P(x_i)\frac{Q(x_i)}{P(x_i)})=-log(\sum _{i=1}^{n}Q(x_i))=0$$

所以KL散度是一个非负值，但是为什么当P和Q相等时，能取到最小值呢？我们单独拿出右边$-{\sum }_{i=1}^{n}P(x_i)log(Q(x_i))$，我们令$C(P,Q)=-{\sum }_{i=1}^{n}P(x_i)log(Q(x_i))$。

我们探索$C(P,P)-C(P,Q)$的正负性来判断P和Q的关系。

$$\begin{array}{rl}C(P,P)-C(P,Q)& =\sum _{i=1}^{n}P(x_i)log(Q(x_i))-\sum _{i=1}^{n}P(x_i)log(P(x_i))\\ & =\sum _{i=1}^{n}P(x_i)log(\frac{Q(x_i)}{P(x_i)})\end{array}$$

因为log(x)是凸函数，所以我们利用jensen不等式，可以得到：

$$a_{1}log(x_1)+a_{2}log(x_2)+\cdots +a_{n}log(x_n)\le log(a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n),(\sum _{i=1}^n{a}_i=1)$$

我们带入${\sum }_{i=1}^{n}P(x_i)log(\frac{Q(x_i)}{P(x_i)}$

$$\begin{array}{rl}P(x_1)log(\frac{Q(x_1)}{P(x_1)})+P(x_2)log(\frac{Q(x_2)}{P(x_2)})+\cdots +P(x_n)log(\frac{Q(x_n)}{P(x_n)})& \le log(P(x_1)\frac{Q(x_1)}{P(x_1)}+P(x_2)\frac{Q(x_2)}{P(x_2)}+\cdots +P(x_n)\frac{Q(x_n)}{P(x_n)}\\ \sum _{i=1}^{n}P(x_i)log(\frac{Q(x_i)}{P(x_i)}& \le log(Q(x_1)+Q(x_2)+\cdots +Q(x_n))=0\end{array}$$

所以$C(P,P)-C(P,Q)\le 0$， 即$C(P,P)\le C(P,Q)$，当且仅当 P=Q时等号成立。

交叉熵

通过上面一系列证明，我们可以确定，KL散度可以反映两个概率分布的距离情况。由于P是样本已知的分布，所以我们可以用KL散度反映Q这个模型产出的结果与P的距离。距离越近，往往说明模型的拟合效果越好，能力越强。

我们把上面定义的C(P, Q)带入KL散度的定义，会发现：

$$D_{KL}(P||Q)=\sum _{i=1}^{n}P(x_i)log(\frac{P(x_i)}{Q(x_i)})=\sum _{i=1}^{n}P(x_i)log(P(x_i))+C(P,Q)$$

对于一个确定的样本集来说，$P(x_i)$是定值，所以我们可以抛开左边${\sum }_{i=1}^{n}P(x_i)log(P(x_i))$不用管它，单纯来看右边。右边我们刚刚定义的C(P, Q)其实就是交叉熵。

说白了，交叉熵就是KL散度去除掉了一个固定的定值的结果。KL散度能够反映P和Q分布的相似程度，同样交叉熵也可以，而且交叉熵的计算相比KL散度来说要更为精简一些。

如果我们只考虑二分类的场景，那么$C(P,Q)=-P(x=0)log(Q(x=0))-P(x=1)log(Q(x=1))$

由于$P(x=0)$结果已知，并且：$P(x=0)+P(x=1)=1,Q(x=0)+Q(x=1)=1$。我们令$P(x=0)=y,Q(x=0)=\hat{y}$

所以上式可以变形为：

$$C(P,Q)=-(ylog(\hat{y})+(1-y)log(1-\hat{y}))$$

这个式子就是我们在机器学习书上最常见到的二分类问题的交叉熵的公式在信息论上的解释，我们经常使用，但是很少会有资料会将整个来龙去脉完整的推导一遍。对于我们算法学习者而言，我个人觉得只有将其中的细节深挖一遍，才能真正获得提升，才能做到知其然，并且知其所以然。理解了这些，我们在面试的时候才能真正做到游刃有余。

当然，到这里其实还没有结束。仍然存在一个问题，可以反映模型与真实分布距离的公式很多，为什么我们训练模型的时候单单选择了交叉熵呢，其他的公式不行吗？为什么呢？

分析

我们来实际看个例子就明白了，假设我们对模型：$\hat{y}=\sigma (\theta X)$选择MSE（均方差）作为损失函数。假设对于某个样本x=2，y=0，${\theta }_0=2,{\theta }_1=1$那么$\theta X=4$，此时$\sigma (\theta X)=0.98$。

此时$MSE=\frac{(\sigma (\theta X)-y{)}^2}{2}$。

我们对它求关于$\theta$的偏导：

$$\begin{array}{rl}MS{E}^{\prime }& =(\sigma (\theta X)-y)\cdot {\sigma }^{\prime }(\theta X)\cdot X\\ & =0.98\ast 2\ast \sigma (\theta X)\cdot (1-\sigma (\theta X))\\ & \approx 2\ast 0.98\ast 0.02\\ & \approx 0.04\end{array}$$

所以如果我们通过梯度下降来学习的话，${\theta }_{next}=\theta -0.04\ast \eta \cdot \theta$。

这个式子看起来很正常，但是隐藏了一个问题，就是我们这样计算出来的梯度实在是太小了。通过梯度下降去训练模型需要消耗大量的时间才能收敛。

如果我们将损失函数换成交叉熵呢？

我们回顾一下交叉熵求梯度之后的公式：

$$\frac{\partial }{\partial \theta }J(\theta )=-(\hat{Y}-Y)\cdot X$$

我们带入上面具体的值，可以算出来如果使用交叉上来训练，我们算出来的梯度为1.96，要比上面算出来的0.04大了太多了。显然这样训练模型的收敛速度会快很多，这也是为什么我们训练分类模型采用交叉熵作为损失函数的原因。

究其原因是因为如果我们使用MSE来训练模型的话，在求梯度的过程当中免不了对sigmoid函数求导。而正是因为sigmoid的导数值非常小，才导致了我们梯度下降的速度如此缓慢。那么为什么sigmoid函数的导数这么小呢？我们来看下它的图像就知道了：

观察一下上面这个图像，可以发现当x的绝对值大于4的时候，也就是图像当中距离原点距离大于4的两侧，函数图像就变得非常平缓。而导数反应函数图像的切线的斜率，显然这些区域的斜率都非常小，而一开始参数稍微设置不合理，很容易落到这些区间里。那么通过梯度下降来迭代自然就会变得非常缓慢。

所以无论是机器学习还是深度学习，我们一般都会少会对sigmoid函数进行梯度下降。在之前逻辑回归的文章当中，我们通过极大似然推导出了交叉熵的公式，今天我们则是利用了信息论的知识推导了交叉熵的来龙去脉。两种思路的出发点和思路不同，但是得到的结果却是同样的。关于这点数学之美当中给出了解释，因为信息论是更高维度的理论，它反映的其实是信息领域最本质的法则。就好像物理学当中公式千千万，都必须要遵守能量守恒、物质守恒一样。机器学习也好，深度学习也罢，无非是信息领域的种种应用，自然也逃不脱信息论的框架。不知道看到这里，你有没有一点豁然开朗和一点震撼的感觉呢？

今天的文章就到这里，公式比较多，但推导过程并不难，希望大家不要被吓住，能冷静看懂。如果觉得有所收获，请顺手扫码点个关注吧，你们的支持是我最大的动力。