交叉熵损失 理解
刚开始学习神经网络解决分类问题时,对交叉熵损失总是理解起来很模糊,不清楚从何而来,为什么用。网上的讲解大部分只侧重一个角度,看了还是云里雾里。
我以至今学习和实践经验,梳理一下个人理解。
数学是对普遍问题的抽象,很多时候我们一开始就看公式会不容易理解。因此我选择先把公式放一放,先直观看一下在深度学习中交叉熵实际上是怎么算的,其实非常简单。
二分类:
| y y y | y ^ \hat y y^ |
|---|---|
| 0.6 | 1 |
y y y表示网络输出,一般是经sigmoid函数后,值域在0到1之间,表示分类概率,0.6表示网络预测60%可能为第二类,40%可能为第一类。
y ^ \hat y y^为标签,0表示真实类别为第一类,1表示真实类别为第二类。
而交叉熵损失是个分段函数:
l o s s = { − log ( 1 − y ) y ^ = 0 − log y y ^ = 1 loss= \begin{cases} -\log (1-y) & \hat y = 0 \\ -\log y & \hat y = 1 \end{cases} loss={−log(1−y)−logyy^=0y^=1
其实就是 − log ( 真 实 类 别 的 预 测 概 率 ) -\log(真实类别的预测概率) −log(真实类别的预测概率):
如果标签为第一类, − log ( 第 一 类 的 预 测 概 率 ) = − log 0.4 -\log(第一类的预测概率)=-\log 0.4 −log(第一类的预测概率)=−log0.4
如果标签为第二类, − log ( 第 二 类 的 预 测 概 率 ) = − log 0.6 -\log(第二类的预测概率)=-\log 0.6 −log(第二类的预测概率)=−log0.6
对上述例子,因为 y ^ = 1 \hat y=1 y^=1,所以 l o s s = − log 0.6 loss=-\log0.6 loss=−log0.6。
就那么简单~
而我们常看到的二分类交叉熵公式是这样的:
l o s s = − [ y ^ ⋅ log y + ( 1 − y ^ ) log ( 1 − y ) ] loss= - [ \hat y \cdot \log y + (1 - \hat y) \log (1 - y) ] loss=−[y^⋅logy+(1−y^)log(1−y)]
看起来有点复杂,其实就是分段函数合成一下嘛。
为了过渡到多分类,我们把标签表示成One-Hot形式。
| 类别 | y y y | y ^ \hat y y^ |
|---|---|---|
| 第一类 | 0.4 | 0 |
| 第二类 | 0.6 | 1 |
交叉熵的值就是 y ^ \hat y y^为1的类别对应的 − log y -\log y −logy。
多分类:
| 类别 | y y y | y ^ \hat y y^ |
|---|---|---|
| 第一类 | 0.3 | 0 |
| 第二类 | 0.5 | 1 |
| 第三类 | 0.2 | 0 |
多分类的 y y y为经Softmax后和为1的各分类概率, y ^ \hat y y^为One-Hot形式。
算法是一样的, y ^ \hat y y^为1的类别对应的 − log y -\log y −logy,即 l o s s = − log 0.5 loss=-\log 0.5 loss=−log0.5。
直观上看,错误类对应的交叉熵损失为0,梯度下降法减少损失,其实就只是增大正确类的预测概率,前边加了个 l o g log log。
深度学习中的实际实现,就是这么简单,同学们不用怀疑。作为严谨的博主,我特意在Pytorch上验证过,对单个样本的交叉熵就是这么算的,当然批量计算的时候还有后续操作。
好了,接着我们从另外几个角度来看一下这交叉熵是哪来的?什么意思?有何特点?
1.对数似然角度
我们为什么会想到用这种形式作为损失函数呢?
| y y y | y ^ \hat y y^ |
|---|---|
| 0.6 | 1 |
对于二分类,我们把预测概率整理一下:
p = y y ^ ( 1 − y ) 1 − y ^ = { 1 − y y ^ = 0 y y ^ = 1 p=y^{\hat y}(1-y)^{1-\hat y}=\begin{cases} 1-y & \hat y = 0 \\ y & \hat y = 1 \end{cases} p=yy^(1−y)1−y^={1−yyy^=0y^=1
这就是概率论中伯努利分布的概率分布函数。
y y y是关于神经网络参数 θ \theta θ的函数,对一个样本来讲,似然函数就是预测概率:
L ( θ ) = y y ^ ( 1 − y ) ( 1 − y ^ ) L(\theta)={y}^{\hat y}(1-y)^{(1-\hat y)} L(θ)=yy^(1−y)(1−y^)
如果有m个样本,似然函数就是这些概率的乘积:
L ( θ ) = ∏ i = 1 m y i y ^ i ( 1 − y i ) ( 1 − y ^ i ) L(\theta)=\prod_{i=1}^{m}{y_i}^{\hat y_i}(1-y_i)^{(1-\hat y_i)} L(θ)=i=1∏myiy^i(1−yi)(1−y^i)
我们要做的就是找到一组参数 θ \theta θ,使得预测值和真实标签最接近,其实就是要让似然函数的值最大,因此 − L ( θ ) -L(\theta) −L(θ)就可以作为损失函数。指数形式不易求导,所以将等式两边取对数,即得到最终的二分类交叉熵损失函数:
l o s s = − log L ( θ ) = − [ y ^ ⋅ log y + ( 1 − y ^ ) log ( 1 − y ) ] loss=-\log L(\theta)= - [ \hat y \cdot \log y + (1 - \hat y) \log (1 - y) ] loss=−logL(θ)=−[y^⋅logy+(1−y^)log(1−y)]
多个样本累加即可:
l o s s = − ∑ i = 1 m [ y ^ i ⋅ log y i + ( 1 − y ^ i ) log ( 1 − y i ) ] loss= -\sum_{i=1}^m[ \hat y_i \cdot \log y_i + (1 - \hat y_i) \log (1 - y_i) ] loss=−i=1∑m[y^i⋅logyi+(1−y^i)log(1−yi)]
2.信息论角度
为什么推出的这个损失函数要叫交叉熵呢?
交叉熵这个词儿来自信息论,对真实概率分布p和非真实概率分布q,定义交叉熵:
H ( p , q ) = − ∑ i = 1 n p ( x i ) log ( q ( x i ) ) H(p,q)=-\sum_{i=1}^n p(x_i)\log(q(x_i)) H(p,q)=−i=1∑np(xi)log(q(xi))
信息论中涉及的概念比较多,我们只需要知道这是用来度量两个概率分布间的差异即可。
| 类别 | y y y | y ^ \hat y y^ |
|---|---|---|
| 第一类 | 0.3 | 0 |
| 第二类 | 0.5 | 1 |
| 第三类 | 0.2 | 0 |
从这个角度看,交叉熵损失是将One-Hot后的标签看做了概率分布p,真实类别位置概率为1,其他位置为0,如此,输出 y y y和标签 y ^ \hat y y^这两个概率分布的交叉熵为:
H = − ( 0 log 0.3 + 1 log 0.5 + 0 log 0.2 ) = − log 0.5 H=-(0\log0.3+1\log0.5+0\log0.2)=-\log0.5 H=−(0log0.3+1log0.5+0log0.2)=−log0.5
跟我们一开始所说的交叉熵实现完全一样。
我们用极大似然得到的二分类交叉熵损失,由此联系推广至多分类。
需要注意的一个点:分类任务中,一个样本未必只能有一个分类,也就是 y ^ \hat y y^中未必只有一个1,如果有多个1,还是按上述公式计算即可。
3.性质
最后我们看一下交叉熵作为损失有什么特点,以二分类为例,先看 y ^ = 1 \hat y = 1 y^=1时, l o s s = − log y loss=-\log y loss=−logy,图像如下:
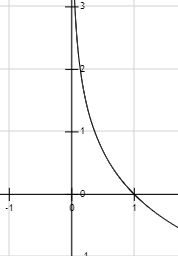
横坐标 y y y的取值范围是 [ 0 , 1 ] [0, 1] [0,1],我们看这一段的图像,当 y y y接近1时,损失接近0,而当 y y y接近0时,损失接近无穷,而且越靠近0,增大越快。当 y ^ = 0 \hat y = 0 y^=0时,图像性质是一样的。
这个性质对损失函数来说是个优点,这意味着损失随 y y y减小而指数式增加,错的越离谱,在梯度下降中优化的力度就更大,这有点像 F o c a l L o s s FocalLoss FocalLoss的意思,强化了对困难样本的学习。而在 y y y接近1时,梯度越来越小,这符合我们梯度下降的优化策略。
二分类交叉熵损失其实最早用于逻辑回归当中,根据吴恩达的课程,逻辑回归中交叉熵损失函数是凸函数,而均方差损失函数是非凸的。同时根据李宏毅的课程,在逻辑回归中这两张损失对2维参数的图像如下:
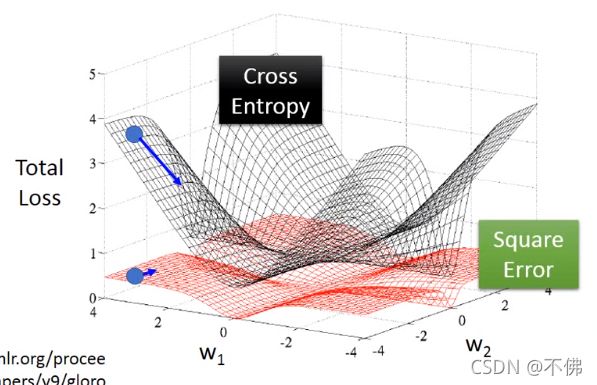
当参数远离最优解时,交叉熵的梯度陡峭,均方差的梯度平坦,这意味着用交叉熵损失训练会更快更容易收敛。
最后还有一个优点,如果损失函数是 S o f t m a x + C r o s s E n t r o p y Softmax+CrossEntropy Softmax+CrossEntropy的组合,在求梯度时将会有很简洁的形式:
∂ E ∂ z i = y ^ i − y i \frac {\partial E}{\partial z_i} = \hat y_i-y_i ∂zi∂E=y^i−yi
E是最终的损失函数, z i z_i zi是网络输出层的第 i i i个元素,就是做 S o f t m a x Softmax Softmax之前的值。
这个结论我就不详细推导了,这个性质相当于少做了两次求导,还是挺有用的,比如 S i g m o i d Sigmoid Sigmoid和 t a n h tanh tanh作为传统激活函数,都具有简化求导的特性。