机器人动力学——拉格朗日法

机器人动力学——拉格朗日法

引文

机器人动力学所用到的运动学方程是一组具有下列形式的二阶微分方程组
$$\tau =M(\theta )\ddot{\theta }+h(\theta ,\dot{\theta })$$
式中，对于所有关节均为驱动关节的开式运动链，广义坐标 $\theta \in {\mathbb{R}}^n$ 表示关节变量；广义力 $\tau \in {\mathbb{R}}^n$ 表示力或力矩，如果 ${\theta }_i$ 是旋转关节，则 ${\tau }_i$ 对应力矩；如果 ${\theta }_i$ 为平动关节，则 ${\tau }_i$ 对应力； $M(\theta )\in {\mathbb{R}}^{n\times n}$ 是一个对称且正定的质量矩阵；$h(\theta ,\dot{\theta })\in {\mathbb{R}}^n$ 是将向心力、科里奥利力、重力和摩擦力等集合在一起的力向量，该向量取决于 $\theta$ 和 $ \dot { \theta}$ 这两个变量。

运动学同样区分正运动学和逆运动学，正向动力学问题是在给定状态变量 $(\theta ,\dot{\theta })$ 以及关节力和力矩的前提下确定机器人的加速度 $\ddot{\theta }$ ，即
$$\ddot{\theta }=M^{-1}(\theta )(\tau -h(\theta ,\dot{\theta }))$$
逆动力学问题则是找到对应于机器人状态和期望加速度的关节力和力矩$\tau$

机器人的动力学方程通常可以通过牛顿-欧拉公式或拉格朗日动力学公式得到。对于简单结构的机器人，如3自由度或自由度更少的情形，拉格朗日形式不仅在概念上十分优雅，并且在实际中非常有效。但对于自由度数目更多的机器人来讲，其计算可能会很快变得烦琐。

下文将讨论拉格朗日动力学公式

拉格朗日函数

力学系统的拉格朗日函数 $\mathcal{L}(q,\dot{q})$ 定义为整个系统的动能 $\mathcal{K}(q,\dot{q})$ 减去势能 $\mathcal{P}(q)$ ，式中的—组独立坐标 $q\in {\mathbb{R}}^n$ 用来描述系统的位形（这个坐标 $q$ 被称为广义坐标）
$$\mathcal{L}(q,\dot{q})=\mathcal{K}(q,\dot{q})-\mathcal{P}(q)$$
运动方程现在可以用拉格朗日函数表示如下（推导过程略，详见动力学教材）
$$f=\frac{d}{dt}\frac{\partial \mathcal{L}}{\partial \dot{q}}-\frac{\partial \mathcal{L}}{\partial q}$$
这个方程也称为含外力的欧拉-拉格朗日方程（在标准形式的欧拉-拉格朗日方程中，外力 $f$ 等于零）

$2R$ 开链机器人举例

下面以在重力作用下的—个 $2R$ 开链机器人为例推导动力学方程，如下图所示

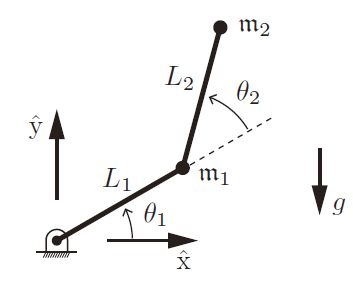
将关节坐标 $\theta =({\theta }_1,{\theta }_2)$ 选做广义坐标，广义力 $\tau =({\tau }_1,{\tau }_2)$ 则对应于关节力矩（因为 ${\tau }^T\dot{\theta }$ 对应于功率）。本例中的拉格朗日函数 $\mathcal{L}(q,\dot{q})$ 可以写成如下分量形式:
$$\mathcal{L}(\theta ,\dot{\theta })=\sum _{i=1}^2({\mathcal{K}}_i-{\mathcal{P}}_i)$$
则欧拉-拉格朗日方程可以写成如下分量形式（ $\tau$ 为关节力和力矩向量）:
$${\tau }_i=\frac{d}{dt}\frac{\partial \mathcal{L}}{\partial \dot{{\theta }_i}}-\frac{\partial \mathcal{L}}{\partial {\theta }_i}i=1,2$$
下面我们需要计算两杆的动能和势能（认为两杆各自的质量 $\mathrm{m}1$ 和 $\mathrm{m}2$ 均集中于各杆末端）

连杆1质心的位置和速度:
$$\begin{array}{l}\left[\begin{array}{l}{x}_1\\ y_1\end{array}\right]=\left[\begin{array}{c}{L}_1\cos {\theta }_1\\ L_1\sin {\theta }_1\end{array}\right]\\ \left[\begin{array}{c}{\dot{x}}_1\\ {\dot{y}}_1\end{array}\right]=\left[\begin{array}{r}-L_1\sin {\theta }_1\\ L_1\cos {\theta }_1\end{array}\right]{\dot{\theta }}_1\end{array}$$
连杆2质心的位置和速度:
$$\begin{array}{l}\left[\begin{array}{l}{x}_2\\ y_2\end{array}\right]=\left[\begin{array}{c}{L}_1\cos {\theta }_1+L_2\cos ({\theta }_1+{\theta }_2)\\ L_1\sin {\theta }_1+L_2\sin ({\theta }_1+{\theta }_2)\end{array}\right]\\ \left[\begin{array}{l}{\dot{x}}_2\\ {\dot{y}}_2\end{array}\right]=\left[\begin{array}{rr}-L_1\sin {\theta }_1-L_2\sin ({\theta }_1+{\theta }_2)& -L_2\sin ({\theta }_1+{\theta }_2)\\ L_1\cos {\theta }_1+L_2\cos ({\theta }_1+{\theta }_2)& L_2\cos ({\theta }_1+{\theta }_2)\end{array}\right]\left[\begin{array}{l}{\dot{\theta }}_1\\ {\dot{\theta }}_2\end{array}\right]\end{array}$$
由 $\mathcal{K}=\frac{1}{2}\mathfrak{m}{v}^2=\frac{1}{2}\mathfrak{m}({\dot{x}}^2+{\dot{y}}^2)$ ，连杆的动能项 ${\mathcal{K}}_1$ 和 ${\mathcal{K}}_2$ 分别为
$$\begin{array}{rl}{\mathcal{K}}_1& =\frac{1}{2}{\mathfrak{m}}_1({\dot{x}}_1^2+{\dot{y}}_1^2)\\ & =\frac{1}{2}{\mathfrak{m}}_1{L}_1^2{\dot{\theta }}_1^2\\ {\mathcal{K}}_2& =\frac{1}{2}{\mathfrak{m}}_2({\dot{x}}_2^2+{\dot{y}}_2^2)\\ & =\frac{1}{2}{\mathfrak{m}}_2((L_1^2+2L_1{L}_2\cos {\theta }_2+L_2^2){\dot{\theta }}_1^2+2(L_2^2+L_1{L}_2\cos {\theta }_2){\dot{\theta }}_1{\dot{\theta }}_2+L_2^2{\dot{\theta }}_2^2)\end{array}$$
势能只取决于高度，即 $y$ 坐标。由 $\mathcal{P}=\mathfrak{m}gy$ ，连杆的势能项 ${\mathcal{P}}_1$ 和 ${\mathcal{P}}_2$ 分别为
$$\begin{array}{l}{\mathcal{P}}_1={\mathfrak{m}}_{1}g{y}_1={\mathfrak{m}}_{1}g{L}_1\sin {\theta }_1\\ {\mathcal{P}}_2={\mathfrak{m}}_{2}g{y}_2={\mathfrak{m}}_{2}g(L_1\sin {\theta }_1+L_2\sin ({\theta }_1+{\theta }_2))\end{array}$$
将动能项与势能项带入拉格朗日函数即可得到平面 $2R$ 运动链的动力学方程:
$$\{\begin{array}{rl}{\tau }_1=& ({\mathfrak{m}}_1{L}_1^2+{\mathfrak{m}}_2(L_1^2+2L_1{L}_2\cos {\theta }_2+L_2^2)){\ddot{\theta }}_1\\ & +{\mathfrak{m}}_2(L_1{L}_2\cos {\theta }_2+L_2^2){\ddot{\theta }}_2-{\mathfrak{m}}_2{L}_1{L}_2\sin {\theta }_2(2{\dot{\theta }}_1{\dot{\theta }}_2+{\dot{\theta }}_2^2)\\ & +({\mathfrak{m}}_1+{\mathfrak{m}}_2)L_{1}g\cos {\theta }_1+{\mathfrak{m}}_{2}g{L}_2\cos ({\theta }_1+{\theta }_2),\\ {\tau }_2=& {\mathfrak{m}}_2(L_1{L}_2\cos {\theta }_2+L_2^2){\ddot{\theta }}_1+{\mathfrak{m}}_2{L}_2^2{\ddot{\theta }}_2+{\mathfrak{m}}_2{L}_1{L}_2{\dot{\theta }}_1^2\sin {\theta }_2\\ & +{\mathfrak{m}}_{2}g{L}_2\cos ({\theta }_1+{\theta }_2).\end{array}$$
可以看到，即使是一个简单的 $2R$ 机器人，其逆运动学方程也十分复杂。对上述各项进行整理，得到如下形式的方程:
$$\tau =M(\theta )\ddot{\theta }+\underset{h(\theta ,\dot{\theta })}{c(\theta ,\dot{\theta })+g(\theta )}$$
式中
$$\begin{array}{rl}M(\theta )& =\left[\begin{array}{cc}{\mathfrak{m}}_1{L}_1^2+{\mathfrak{m}}_2(L_1^2+2L_1{L}_2\cos {\theta }_2+L_2^2)& {\mathfrak{m}}_2(L_1{L}_2\cos {\theta }_2+L_2^2)\\ {\mathfrak{m}}_2(L_1{L}_2\cos {\theta }_2+L_2^2)& {\mathfrak{m}}_2{L}_2^2\end{array}\right]\\ c(\theta ,\dot{\theta })& =\left[\begin{array}{c}-{\mathfrak{m}}_2{L}_1{L}_2\sin {\theta }_2(2{\dot{\theta }}_1{\dot{\theta }}_2+{\dot{\theta }}_2^2)\\ {\mathfrak{m}}_2{L}_1{L}_2{\dot{\theta }}_1^2\sin {\theta }_2\end{array}\right]\\ g(\theta )& =\left[\begin{array}{c}({\mathfrak{m}}_1+{\mathfrak{m}}_2)L_{1}g\cos {\theta }_1+{\mathfrak{m}}_{2}g{L}_2\cos ({\theta }_1+{\theta }_2)\\ {\mathfrak{m}}_{2}g{L}_2\cos ({\theta }_1+{\theta }_2)\end{array}\right]\end{array}$$
式中 $M(\theta )$ 为对称正定的质量矩阵， $c(\theta ,\dot{\theta })$ 为速度乘积项，包含科里奥利和向心力矩的向量，其中包含 ${\dot{\theta }}^2$ 的二次项称为向心项，包含 ${\dot{\theta }}_i{\dot{\theta }}_j(i\ne j)$ 的二次项则称为科里奥利项。 $g(\theta )$ 为重力项 ，因为此处势能仅来自重力，若末端有弹簧，弹簧也会贡献势能。这些揭示了运动方程是 $\ddot{\theta }$ 的线性函数、 $\dot{\theta }$ 的二次函数、 $\theta$ 的三角函数。上述结论不仅适用于 $2R$ 型机器人，对于包含转动关节的串联运动链也同样适用。