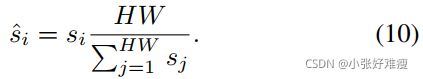【论文总结】DeepEMD:Few-Shot Image Classification with Differentiable Earth Mover’s Distance（附翻译）

DeepEMD:Few-Shot Image Classification with Differentiable Earth Mover’s Distance   使用陆地移动距离的小样本图像分类

论文地址：https://arxiv.org/abs/2003.06777
代码地址：https://github.com/icoz69/DeepEMD

基于度量学习的小样本学习算法：利用一个特征提取网络将支持集图像和查询集图像映射到一个特征空间，然后再设计或选择一种距离度量方式，来描述支持集图像和查询集图像之间的相似程度，并以此进行类别预测。

主要流程：
将图片拆分成多个图块，然后使用Earth Mover’s Distance计算查询集和支持集图像的各个图块之间的最佳匹配流，再通过上面生成的局部Embedding和匹配流来计算两张图片之间的距离，用生成的距离进行分类
相当于将一整幅图像压缩为一个高度抽象的特征向量，并计算两个特征向量之间的距离作为相似性度量的方式而言，通过比较各个局部图块之间的相似程度来反映两幅图像是否属于同一类别，则更为可靠和准确。但如果是每两个图块之间都逐一比对的话，这计算成本也过于高昂，于是作者就利用EMD方法，通过线性规划的方式寻找两幅图像各个图块之间的最佳匹配方式，并且为不同的位置的图块分配了不同的权重，类似于注意力机制，对于目标区域给予更多注意。

---

摘要

In this paper, we address the few-shot classification task from a new perspective of optimal matching between image regions. We adopt the Earth Mover’s Distance (EMD) as a metric to compute a structural distance between dense image representations to determine image relevance. The EMD generates the optimal matching flows between structural elements that have the minimum matching cost, which is used to represent the image distance for classification. To generate the important weights of elements in the EMD formulation, we design a cross-reference mechanism, which can effectively minimize the impact caused by the cluttered background and large intra-class appearance variations. To handle k-shot classification, we propose to learn a structured fully connected layer that can directly classify dense image representations with the EMD. Based on the implicit function theorem, the EMD can be inserted as a layer into the network for end-to-end training. We conduct comprehensive experiments to validate our algorithm and we set new state-of-the-art performance on four popular few-shot classification benchmarks, namely miniImageNet, tieredImageNet, Fewshot-CIFAR100 (FC100) and Caltech-UCSD Birds-200-2011 (CUB).

在本文中，我们从图像区域之间最佳匹配的新角度来解决小样本分类任务。我们采用Earth Mover’s Distance（EMD）作为度量来计算密集图像表示之间的结构距离，以确定图像相关性。EMD生成具有最小匹配代价的结构元素之间的最佳匹配流，用于表示分类的图像距离。为了在EMD公式中生成元素的重要权重，我们设计了一种交叉引用机制，该机制可以有效地最小化背景杂乱和类内外观变化较大所造成的影响。为了处理k-shot分类，我们建议学习一个结构化的完全连接层，该层可以直接使用EMD对密集图像表示进行分类。基于隐函数定理，EMD可以作为一个层插入到网络中进行端到端的训练。我们进行了全面的实验来验证我们的算法，并在四个流行的小样本分类基准上设定了最新的性能，即miniImageNet、tieredImageNet、Fewshot-CIFAR100（FC100）和加州理工大学UCSD Birds-200-2011（CUB）。

介绍

Deep neural networks have achieved breakthroughs in a wide range of visual understanding tasks in the past few years. However, its data-driven nature often makes it struggle when no sufficiently large labeled training data is available. Meta learning, on the other hand, is proposed to learn a model that can quickly generalize to new tasks with minor adaption steps. One of the most well-studied test-bed for meta-learning algorithms is few-shot image classification, which aims to perform classification on new image categories with only a small amount of labeled training data.

在过去几年中，深度神经网络在广泛的视觉理解任务中取得了突破。然而，当没有足够多标记训练数据可用时，它的数据驱动特性常常使它陷入困境。另一方面，元学习被提出学习一个模型，该模型可以通过较小的调整步骤快速推广到新任务。小样本图像分类是元学习算法中研究最为广泛的测试平台之一，其目标是仅使用少量的标记训练数据对新的图像类别进行分类。

To address this problem, a line of the previous literature adopts metric-based methods [30,43,63,66,67,72] that  learn to represent image data in an appropriate feature space and use a distance function to predict image labels. Following the formulation of the standard image classification networks [16, 24, 62], metric-based methods often employ a convolution neural network to learn image feature representations, but replace the fully connected layer with a distance function, e.g., cosine distance and Euclidean distance. Such distance functions directly compute the distance between the embeddings of the test images and training images for classification, which bypasses the difficult optimization problem in learning a classifier for the fewshot setting. The network is trained by sampling from a distribution of tasks, in the hopes of acquiring generalization ability to unseen but similar tasks.

为了解决这个问题，先前文献中的一行采用了基于度量的方法[30,43,63,66,67,72]，该方法学习在适当的特征空间中表示图像数据，并使用距离函数预测图像标签。在制定标准图像分类网络[16、24、62]之后，基于度量的方法通常使用卷积神经网络来学习图像特征表示，但使用距离函数（例如余弦距离和欧氏距离）替换全连接层。这种距离函数直接计算用于分类的测试图像和训练图像的嵌入之间的距离，从而绕过了为小样本设置学习分类器的困难优化问题。该网络通过从任务分布中取样进行训练，以期获得对未知但相似任务的泛化能力。

Despite their promising results, we observe that the cluttered background and large intra-class appearance variations may drive the image-level embeddings from the same category far apart in a given metric space. Although the problem can be alleviated by the neural network under the fully supervised training, thanks to the activation functions and abundant training images, it is almost inevitably amplified in low-data regimes and thus negatively impacts the image classification. Moreover, a mixed global representation destroys image structures and loses local features. Local features can provide discriminative and transferable information across categories, which can be important for image classification in the few-shot scenario. Therefore, a desirable metric-based algorithm should have the ability to utilize the local discriminative representations for metric learning and minimize the impact caused by the irrelevant regions.

尽管它们的结果是很好的，但我们观察到，杂乱的背景和类内外观变化较大可能会导致来自同一类别的图像级映射在给定的度量空间中相距很远。尽管在完全监督的训练下，神经网络可以缓解这一问题，但由于激活函数和丰富的训练图像，它几乎不可避免地在低数据区域被放大，从而对图像分类产生负面影响。此外，混合全局表示会破坏图像结构并丢失局部特征。局部特征可以提供跨类别的区分性和可转移信息，这对于小样本场景中的图像分类非常重要。因此，一个理想的基于度量的算法应该能够利用局部判别表示进行度量学习，并最小化不相关区域造成的影响。

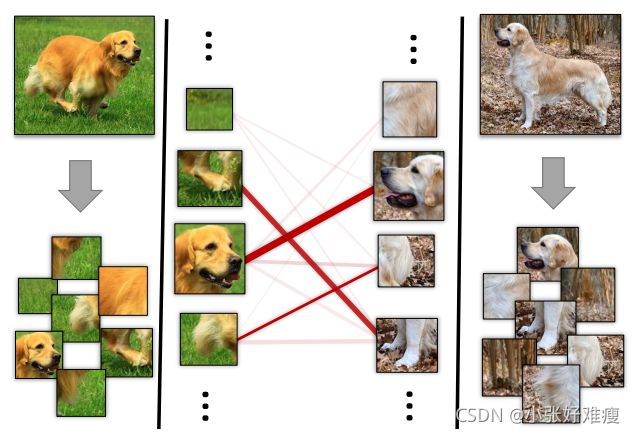
A natural way to compare two complex structured representations is to compare their building blocks. The difficulty lies in that we do not have their correspondence supervision for training and not all building elements can always find their counterparts in the other structures. To solve the problems above, in this paper, we formalize the few-shot classification as an instance of optimal matching, and we propose to use the optimal matching cost between two structures to represent their similarity. Given the feature representations generated by two images, we adopt the Earth Mover’s Distance (EMD) [50] to compute their structural similarity. EMD is the metric for computing distance between structural representations, which was originally proposed for image retrieval. Given the distance between all element pairs, EMD can acquire the optimal matching flows between two structures that have the minimum cost. It can also be interpreted as the minimum cost to reconstruct a structure representation with the other one. An illustration of our motivation is shown in Fig. 1. EMD has the formulation of the transportation problem [17] and the global minimum can be achieved by solving a Linear Programming problem. To embed the optimization problem into the model for end-to-end training, we can apply the implicit function theorem [3,8,22] to form the Jacobian matrix of the optimal optimization variable with respect to the problem parameters [3].

比较两种复杂结构化表示的方法是比较它们的构建模块。困难在于我们没有他们的通信监督进行训练，而且并非所有框架结构都能在其他结构中找到对应物。为了解决上述问题，本文将小样本分类形式化为最优匹配的一个实例，并提出用两个结构之间的最优匹配代价来表示它们的相似性。给定由两幅图像生成的特征表示，我们采用Earth Mover’s Distance（EMD）[50]来计算它们的结构相似性。EMD是计算结构表示之间距离的度量，最初是为图像检索而提出的。在给定单元对间距的情况下，EMD可以获得代价最小的两种结构之间的最优匹配流。它也可以解释为用另一个结构表示法重建结构表示法的最小成本。图1显示了我们的动机。EMD具有运输问题的公式[17]，通过求解线性规划问题可以实现全局最小值。为了将优化问题嵌入到端到端训练模型中，我们可以应用隐函数定理[3,8,22]来形成最优优化变量相对于问题参数的雅可比矩阵[3]。

Figure 1: Illustration of using Earth Mover’s Distance for one-shot image classification. Our algorithm uses optimal matching cost between image regions to represent the image distance.  使用Earth Mover’s Distance进行一次拍摄图像分类的图示。我们的算法使用图像区域之间的最佳匹配代价来表示图像距离。

An important problem parameter in the EMD formulation is the weight of each element. Elements with large weights generate more matching flows and thus contribute more to the overall distance. Ideally, the algorithm should have the flexibility to assign less weight on irrelevant regions such that they contribute less to the overall distance no matter which elements they match with. To achieve this goal, we propose a cross-reference mechanism to determine the importance of the elements. In our cross-reference mechanism, each node is determined by comparing it with the global statistics of the other structure. This aims to give less weight to the high-variance background regions and the object parts that are not co-occurrent in two images.

EMD公式中的一个重要问题参数是每个元素的权重。具有较大权重的单元会生成更多匹配流，从而对总距离的贡献更大。理想情况下，算法应该具有灵活性，在不相关的区域上分配较少的权重，这样无论与哪些元素匹配，它们对总距离的贡献都较小。为了实现这一目标，我们提出了一种交叉引用机制来确定元素的重要性。在我们的交叉引用机制中，每个节点都是通过与其他结构的全局统计数据进行比较来确定的。这旨在降低高方差背景区域和两幅图像中不同时出现的目标部分的权重。 

In the k-shot setting where multiple support images are presented, we propose to learn a structured fully connected (FC) layer as the classifier for classification to make use of the increasing number of training images. The structured FC layer includes a group of learnable vectors for each class. At inference time, we use the EMD to compute the distance between the image embeddings and the learnable vector set in each class for classification. The structured FC is an extension of the standard fully connected layer in that it replaces dot product operations between vectors with EMD function between vector sets such that the structured FC layer could directly classify feature maps. The structured FC layer can also be interpreted as learning a prototype embedding from a dummy image for each category such that the test images can be matched with them for classification.

在k-shot设置中，多个支持图像被呈现，我们建议学习一个结构化的完全连接（FC）层作为分类器进行分类，以利用不断增加的训练图像数量。结构化FC层为每个类包括一组可学习向量。在推理时，我们使用EMD计算图像嵌入与每个类别中可学习向量集之间的距离，以进行分类。结构化FC是标准全连接层的扩展，它使用向量集之间的EMD函数替换向量之间的点积运算，从而结构化FC层可以直接对特征地图进行分类。结构化FC层也可以解释为从每个类别的虚拟图像学习原型映射，以便测试图像可以与其匹配以进行分类。

To validate our algorithm, we conduct extensive experiments on multiple datasets to demonstrate the effectiveness of our algorithm. Our main contributions are summarizedas follows:
• We propose to formalize the few-shot image classification as an optimal matching problem and adopt the Earth Mover’s Distance as the distance metric between structured representations. The EMD layer can be embedded into the network for end-to-end training.
• We propose a cross-reference mechanism to generate the weights of elements in the EMD formulation, which can effectively reduce the noise introduced by the background regions in the images.
• We propose to learn a structured fully connected layer in the k-shot settings, which could directly classify the structural representations of an image using the Earth Mover’s Distance.
• Experiments on four popular few-shot classification benchmark datasets—miniImagenet, tieredImagenet, FC100 and CUB, show that our algorithm on both 1-shot and 5-shot tasks significantly outperforms the baseline methods and achieves new state-of-the-art performance on all of them.

为了验证我们的算法，我们在多个数据集上进行了大量实验，以证明我们算法的有效性。我们的主要贡献总结如下：
•我们建议将小样本图像分类形式化为一个最佳匹配问题，并采用Earth Mover’s Distance作为结构化表示之间的距离度量。EMD层可以嵌入到网络中进行端到端的训练。
•我们提出了一种交叉参考机制来生成EMD公式中元素的权重，它可以有效地减少图像中背景区域引入的噪声。
•我们建议在k-shot设置中学习一个结构化的完全连接层，该层可以使用地球移动器的距离直接对图像的结构表示进行分类。
•在四个常用的小样本分类基准数据集miniImagenet、tieredImagenet、FC100和CUB上的实验表明，我们的算法在1-shot 和5-shot 任务上都显著优于基线方法，并在所有这些方法上实现了最新的性能。

相关工作

Few-Shot Learning. There are two main streams in the few-shot classification literature, metric-based approaches and optimization-based approaches. Optimization-based methods [2, 5, 9–11, 18, 26, 31–33, 36, 38, 40–42, 44, 46, 47, 54, 55, 58, 64, 78] target at effectively adapting model parameters to new tasks in the low-shot regime. Our method is more related to the metric-based methods [30, 43, 63, 66, 67, 72], which aim to represent samples in an appropriatefeature space where data from different categories can be distinguished with distance metrics. To achieve this goal,most previous methods represent the whole image as a data point in the feature space. There are also some works making predictions based on local features. For example, Lifchitz et al. [33] directly make predictions with each local feature and fuse their results. Li et al. [30] adopt k-NN to fuse local distance. Our solution to the k-shot problem also draws connections to optimization-based methods since that we learn a classifier that can directly classify structured representations with Earth Mover’s Distance, which can benefit from the increasing number of support samples.

小样本学习    在为小样本分类文献中，有两大主流：基于度量的方法和基于优化的方法。基于优化的方法[2,5,9-11,18,26,31-33,36,38,40-42,44,46,47,54,55,58,64,78]旨在有效地使模型参数适应 low-shot的新任务。我们的方法与基于度量的方法更相关[30、43、63、66、67、72]，其目的是在适当的特征空间中表示样本，其中不同类别的数据可以通过距离度量进行区分。为了实现这一目标，以前的大多数方法都将整个图像表示为特征空间中的一个数据点。也有一些方法根据本地特征进行预测。例如，Lifchitz等人[33]直接利用每个局部特征进行预测，并融合其结果。Li等人[30]采用k-NN融合局部距离。我们对k-shot问题的解决方案还与基于优化的方法建立了联系，因为我们学习了一种分类器，该分类器可以直接根据地球移动器距离对结构化表示进行分类，这可以受益于越来越多的支持样本。

Apart from the two popular branches, many other promising methods are also proposed to handle the few-shot classification problem, such as works based on graph theories [13, 15, 21], reinforcement learning [6], differentiable SVM [25], temporal convolutions [39], etc. [4, 12, 14, 20, 27,28,37,45,49,57,60,61,65,69–71,75,76].

除了这两个流行的分支外，还提出了许多其他有希望的方法来处理小样本分类问题，例如基于图论[13,15,21]、强化学习[6]、可微支持向量机[25]、时间卷积[39]等[4,12,14,20,27,28,37,45,49,57,60,61,65,69-71,75,76]。

Other related topics. Besides image classification, fewshot learning is also investigated in other computer vision tasks, such as image segmentation [34, 73, 74]. There are also some previous works related to the techniques adopted in this paper. For example, Schulter et al. [56] solve the multi-object tracking problem with a network flow formulation. Zhao et al. [77] propose to use the differential EMD to handle visual tracking problem based on the sensitivity analysis of the simplex method. Li [29] uses a tensor-SIFTbased EMD to tackle contour tracking problem.

其他相关    除了图像分类外，小样本学习还可用于其他计算机视觉任务，如图像分割[34,73,74]。也有一些以前的工作与本文所采用的技术有关。例如，Schulter等人[56]利用网络流公式解决了多目标跟踪问题。Zhao等人[77]基于单纯形法的灵敏度分析，建议使用微分EMD处理视觉跟踪问题。Li[29]使用基于张量SIFTB的EMD处理轮廓跟踪问题。

方法

In this section, we first present a brief review of the Earth Mover’s Distance and describe how we formulate the one-shot classification as an optimal matching problem that can be trained end-to-end. Then, we describe our crossreference mechanism to generate the weight of each node, which is an important parameter in the EMD formulation. Finally, we demonstrate how to use the EMD distance function to handle k-shot learning with our proposed structured fully connected layer. The overview of our framework for one-shot classification is shown in Fig. 2.

在本节中，我们首先简要回顾了Earth Mover’s Distance，并描述了我们如何将一次性分类表述为可端到端训练的最佳匹配问题。然后，我们描述了生成每个节点权重的交叉参考机制，这是EMD公式中的一个重要参数。最后，我们演示了如何使用EMD距离函数处理我们提出的结构化全连接层的k-shot学习。图2显示了我们的one-shot分类框架的概述。

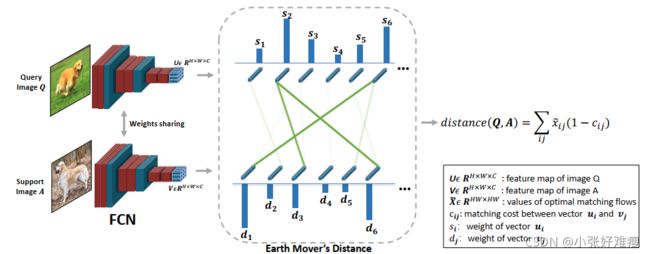
Figure 2: Our framework for 1-shot image classification. Given a pair of images, we first use a Fully Convolutional Network to generate dense representations of them, which contain two sets of feature vectors. The model generates the weights of all vectors with our proposed cross-reference mechanism (not indicated in the figure). Then we use the Earth Mover’s Distance to generate the optimal matching flows between two sets that have the minimum overall matching cost. Finally, based on the optimal matching flows and matching costs, we can compute the distance between two images, which are used for classification. 1-shot图像分类框架。给定一对图像，我们首先使用全卷积网络来生成它们的密集表示，其中包含两组特征向量。该模型使用我们提出的交叉参考机制（图中未显示）生成所有向量的权重。然后，我们使用地球移动器的距离来生成具有最小总体匹配成本的两组之间的最佳匹配流。最后，根据最佳匹配流和匹配代价计算两幅图像之间的距离用于分类。

3.1. Revisiting Earth Mover’s Distance

The Earth Mover’s Distance is a distance measure between two sets of weighted objects or distributions, which is built upon the basic distance between individual objects. It has the form of the well-studied transportation problem (TP) from Linear Programming. Specially, suppose that a set of sources or suppliers S = {si | ji = 1; 2; ...m} are required to transport goods to a set of destinations or demanders D = {dj | jj = 1; 2; ...k}, where si denotes the supply units of supplier i and dj represents the demand of j-th demander. The cost per unit transported from supplier i to demander j is denoted by cij , and the number of units transported is denoted by xij. The goal of the transportation problem is then to find a least-expensive flow of goods   from the suppliers to the demanders:

Earth Mover’s Distance是两组加权对象或分布之间的距离度量，它建立在单个目标之间的基本距离之上。它的形式是经过充分研究的线性规划运输问题（TP）。特别地，假设需要一组来源或供应商S={si | ji=1；2；..m}将货物运输到一组目的地或需求方D={dj | jj=1；2；..k}，其中si表示供应商i的供应单位，dj表示第j个需求方的需求。从供方i向需方j运输的单位成本用cij表示，运输的单位数量用xij表示。运输问题的目标是找到从供应商到需求方的最便宜的货物流：
​

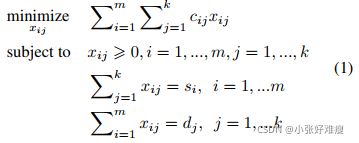
Note that roles of suppliers and demanders can be switched without affecting the total transportation cost. si and dj are also called the weights of the nodes, which controls the total matching flows generated by each node. EMD seeks an optimal matching X~ between suppliers and demanders such that overall matching cost can be minimized. The global optimal matching flows X~ be achieved by solving the Linear Programming problem.

注意，在不影响总运输成本的情况下，可以切换供应商和需求方的角色。si和dj也称为节点的权重，控制每个节点生成的总匹配流。EMD寻求供应商和需求方之间的最优匹配X~以使总体匹配成本最小化。通过求解线性规划问题，可以得到全局最优匹配流X~。

3.2. EMD for Few-Shot Classification

In the few-shot classification task, metric-based methods aim to find a good distance metric and data representations to compute the similarity between images, which are used for classification. Different from the previous methods that perform distance computation between the image-level embeddings, our approach advocates the use of discriminative local information. We decompose an image into a set of local representations and use the optimal matching cost between two images to represent their similarity. Concretely, we first deploy a fully convolutional network (FCN) [59] to generate the image embedding U ∈ RH×W ×C, where H and W denote the spatial size of the feature map and C isthe feature dimension. Each image representation contains a collection of local feature vectors [u1; u2;... uHW ], and each vector ui can be seen as a node in the set. Thus, the similarity of two images can be represented as the optimal matching cost between two sets of vectors. Following theoriginal EMD formulation in Equation 1, the cost per unit is obtained by computing the pairwise distance between embedding nodes ui, vj from two image features:

在小样本分类任务中，基于度量的方法旨在找到一个良好的距离度量和数据表示来计算用于分类的图像之间的相似性。与以往的图像级嵌入之间进行距离计算的方法不同，我们的方法提倡使用有区别的局部信息。我们将一幅图像分解为一组局部表示，并使用两幅图像之间的最佳匹配代价来表示它们的相似性。具体地说，我们首先部署一个全卷积网络（FCN）[59]来生成图像嵌入U∈ RH×W×C，其中H和W表示特征图的空间大小，C表示特征尺寸。每个图像表示都包含一组局部特征向量[u1；u2；…uHW]，每个向量ui都可以看作集合中的一个节点。因此，两幅图像的相似性可以表示为两组向量之间的最佳匹配代价。根据方程1中的原始EMD公式，通过从两个图像特征计算嵌入节点ui、vj之间的成对距离来获得单位成本：

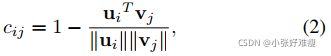
where nodes with similar representations tend to generate fewer matching cost between each other. As to the generation of weights si and dj, we leave the detailed elaborations in Section 3.4. Once acquiring the optimal matching flows X~, we can compute the similarity score s between image representations with:

其中，具有相似表示的节点倾向于在彼此之间生成较少的匹配成本。关于权重si和dj的生成，我们将在第3.4节中进行详细阐述。一旦获得最佳匹配流X~，我们可以使用以下公式计算图像表示之间的相似性分数s：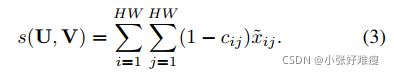

3.3. End-to-End Training

In order to embed the optimal matching problem into a neural network for end-to-end training, it is helpful to make the solution of the optimal matching X~ be differentiable with respect to the problem parameters θ. As is indicated by [3], we can apply implicit function theorem [3,8,22] on the optimality (KKT) conditions to obtain the Jacobian. For the sake of completeness, we start with Equation 1 which is assigned compactly in matrix form:

为了将最优匹配问题映射到神经网络中进行端到端训练，使最优匹配X~的解相对于问题参数θ可微是有帮助的。如[3]所示，我们可以在最优性（KKT）条件下应用隐函数定理[3,8,22]来获得 Jacobian矩阵。为了完整性，我们从方程式1开始，方程式1以矩阵形式紧凑分配：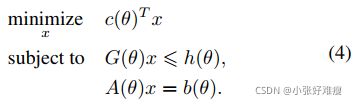

Here x ∈ Rn is our optimization variable, with n = HW × HW representing the total number of matching flows in X . θ is the problem parameter that relates to the earlier layers in a differentiable way. Ax = b represents the equality constraints and Gx ≤ h denotes the inequality constraint in Equation 1. Accordingly, the Lagrangian of the LP problem in equation 4 is given by:

这里是x∈ Rn是我们的优化变量，n=HW×HW表示X中匹配流的总数。θ是以可微方式与早期层相关的问题参数。Ax=b表示等式约束和Gx≤ h表示等式1中的不等式约束。因此，方程式4中LP问题的拉格朗日公式如下所示：

where ν are the dual variables on the equality constraints and λ ≥ 0 are the dual variables on the inequality constraints.

式中，ν是等式约束和λ上的对偶变量≥ 0是不等式约束上的对偶变量。

Following the KKT conditions with notational convenience, we can obtain the optimum of the objective function by solving with primal-dual interior point methods, where

​在KKT条件下，利用原始-对偶内点法求解，得到目标函数的最优，其中
​


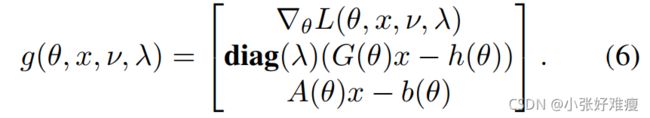
Then, the following theorem holds to help us derive the gradients of the LP parameters.下面的定理有助于我们推导LP参数的梯度。
Theorem 1 (From Barratt [3]) Suppose . Then, when all derivatives exist, the partial Jacobian of x with respect to θ at the optimal solution , namely Jθx~, can be obtained by satisfying:

定理1（来自Barratt[3]）假设。然后，当所有导数都存在时，可通过满足以下条件获得最优解处x相对于θ的部分Jacobian矩阵，即Jθx~：
​

Here the formula for the Jacobian of the solution mapping is obtained by applying the implicit function theorem to the KKT conditions. For instance, the (partial) Jacobian with respect to θ can be defined as

将隐函数定理应用于KKT条件，得到了解映射的雅可比矩阵公式。例如，关于θ的（部分）Jacobian矩阵可以定义为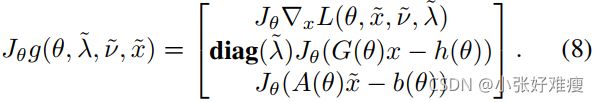

Therefore, once getting the optimal solution x~ for the LP problem, we can obtain a closed-form expression for the gradient of x~ with respect to the input LP parameters θ. This helps us achieve an efficient backpropagation through the entire optimization process without perturbation of the initialization and optimization trajectory.

因此，一旦得到LP问题的最优解x~，我们就可以得到x~相对于输入LP参数θ的梯度的一个闭式表达式。这有助于我们在整个优化过程中实现高效的反向传播，而不会扰动初始化和优化轨迹。

3.4. Weight Generation

As can be observed in the EMD formulation, an important problem parameter is the weight of each node, e.g., si, which controls the total matching flows from it. Intuitively, the node with a larger weight plays a more important role in the comparison of two sets, while a node
with a very small weight can hardly influence the overall distance no matter which nodes it matches with. In the pioneering work that adopts EMD for color-based image retrieval [50], they use the histogram as the elementary feature and perform feature clustering over all pixels to generate the nodes. The weight of each node is set as the size of the corresponding cluster. It makes sense because for color-based image retrieval, large weight should be given to the dominant colors with more pixels, such that the retrieved images can be visually close to the query images.

​从EMD公式中可以观察到，一个重要的问题参数是每个节点的权重，例如si，它控制来自它的总匹配流。直观地说，权重较大的节点在两个集合的比较中起着更重要的作用，而一个节点
如果权重很小，则无论与哪个节点匹配，都很难影响总体距离。在采用EMD进行基于颜色的图像检索的开创性工作[50]中，他们使用直方图作为基本特征，并对所有像素执行特征聚类以生成节点。每个节点的权重设置为相应集群的大小。这是有意义的，因为对于基于颜色的图像检索，应该为具有更多像素的主颜色赋予较大的权重，以便检索的图像可以在视觉上接近查询图像。

​However, for few-shot image classification tasks where features for classification often have high-level semantic meanings, the number of pixels does not necessarily reflect the importance. It is common to find image data with greater background regions than the target objects in classification datasets, e.g., ImageNet. Thus, the importance of a local feature representation can hardly be determined only by inspecting individual images alone. Instead, we argue that for the few-shot classification task, the weights of node features should be generated by comparing the nodes on both sides. To achieve this goal, we propose a crossreference mechanism that uses dot product between a node feature and the average node feature in the other structure to generate a relevance score as the weight value:

​然而，对于小样本图像分类任务，其中用于分类的特征通常具有高级语义，像素的数量不一定反映重要性。在分类数据集中，通常会发现背景区域大于目标对象的图像数据，例如ImageNet。因此，仅通过检查单个图像很难确定局部特征表示的重要性。相反，我们认为对于小样本分类任务，应该通过比较两侧的节点来生成节点特征的权重。为了实现这一目标，我们提出了一种交叉参考机制，该机制使用另一个结构中的节点特征和平均节点特征之间的点积来生成相关性得分作为权重值：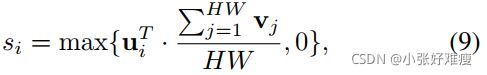

where ui and vj denotes the vectors from two feature maps, and function max(·) ensures the weights are always nonnegative. For clarity, here we simply take si as an example and di can be obtained in the same manner. The crossreference mechanism aims to give less weight to the highvariance background regions and more to the co-occurrent object regions in two images. This can also put less weight on the object parts that do not occur in two images and thus allows partial matching to some extent. Finally, we normalize all the weights in the structure to make both sides have the same total weights for matching:

其中ui和vj表示来自两个特征映射的向量，函数max（·）确保权重始终为非负。为了清楚起见，这里我们仅以si为例，并且可以以相同的方式获得di。交叉参考机制的目的是在两幅图像中对高方差背景区域赋予较少的权重，而对共现目标区域赋予更多的权重。这还可以减少两幅图像中未出现的目标部分的权重，从而在一定程度上允许部分匹配。最后，我们对结构中的所有权重进行归一化，以使两侧具有相同的总权重进行匹配：

3.5. Structured Fully Connected Layer

Thus far we have discussed using the Earth Mover’s Distance as the metric to generate the distance value between paired images. A question is then raised—how do we handle the k-shot setting where multiple support images are available? Before presenting our design in detail, let us have a review of how the standard fully layer classify an image embedding extracted by CNNs. A FC layer, parameterized by contains a set of learnable vectors Φi ∈ RC corresponding to each category. At inference time, given an image embedding u ∈ RC generated by the convolutional layer, the FC layer generates the score of a class i by computing the dot product between the image vector u and the parameter vector Φi, and this process is applied to all the categories in parallel by matrix multiplication. There are also some previous works replacing the dot product operation in the FC layer with the cosine function for computing the category scores [5,53]. The learning of the FC layer can be seen as finding a prototype vector for each class such that we can use distance metrics to classify an image. An illustration of the standard FC layer is shown in Fig. 3 (a).

​到目前为止，我们已经讨论了使用Earth Mover’s Distance 作为度量来生成成对图像之间的距离值。然后提出了一个问题，在多个支持图像可用的情况下，我们如何处理k-shot设置？在详细介绍我们的设计之前，让我们回顾一下标准的全层分类是如何对CNN提取的图像嵌入进行分类的。由参数化的FC层包含一组可学习向量Φi∈ 对应于每个类别的RC。在推理时，给定一个嵌入图像u∈ 由卷积层生成的RC，FC层通过计算图像向量u和参数向量Φi之间的点积生成i类分数，该过程通过矩阵乘法并行应用于所有类别。还有一些以前的工作将FC层中的点积运算替换为计算类别分数的余弦函数[5,53]。FC层的学习可以看作是为每个类找到一个原型向量，这样我们就可以使用距离度量对图像进行分类。标准FC层的图示如图3（a）所示。

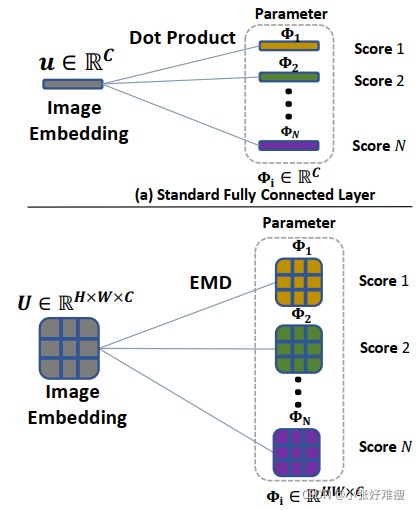
​With the same formulation, we can learn a structured fully connected layer that adopts EMD as the distance function to directly classify a structured feature representation. The learnable embedding for each class becomes a group of vectors, rather than one vector, such that we can use the structured distance function EMD to undertake image classification. This can also be interpreted as learning a prototype feature map generated by a dummy image for each class. The comparison of the structured FC and the standard FC can be found in Fig. 3. At inference time, we fix the trained 1-shot FCN model as the feature extractor and use SGD to learn the parameters in the structured fully connected layer by sampling data from the support set.

​使用相同的公式，我们可以学习一个结构化的完全连通层，该层采用EMD作为距离函数，直接对结构化特征表示进行分类。每个类的可学习嵌入成为一组向量，而不是一个向量，因此我们可以使用结构化距离函数EMD进行图像分类。这也可以解释为学习由每个类的虚拟图像生成的原型特征图。结构化FC和标准FC的比较如图3所示。在推理时，我们将训练好的1-shot FCN模型作为特征提取器，并使用SGD从支持集采样数据来学习结构化全连通层中的参数。

Figure 3: Comparison of standard fully connected layer (a) and our proposed structured fully connected layer (SFC) (b). The SFC learns a group of vectors as the prototype for each class such that we can use the EMD to generate category scores. 比较标准全连接层（a）和我们提出的结构化全连接层（SFC）（b）。SFC学习一组向量作为每个类别的原型，这样我们可以使用EMD生成类别分数。

4  实验

To evaluate the performance of our proposed algorithm for few-shot classification, we conduct extensive experiments on multiple datasets. In this section, we first present dataset information and some important implementation details in our network design. Then, we conduct various ablative experiments to validate each component in our network. Finally, we compare our model with the state-of-theart methods on popular benchmark datasets.

为了评估我们提出的小样本分类算法的性能，我们在多个数据集上进行了大量实验。在本节中，我们首先介绍数据集信息和网络设计中的一些重要实现细节。然后，我们进行各种消融实验来验证我们网络中的每个组件。最后，我们将我们的模型和流行基准数据集上的最新方法进行了比较。

4.1. Implementation Details

For a fair comparison with previous works, we employ a 10-layer ResNet (ResNet10) as our model backbone, which is widely used in the few-shot classification literature. We transform it into a fully convolutional manner by removing the fully connected layer. Specifically, given an image of size 84 × 84, the model generates a feature map of size m5 × 5 × 512, i.e. 25 512-dimensional vectors. We adopt the GPU accelerated Convex solver QPTH [1] to solve the Linear Programming problem in our network and compute gradients for back-propagation. As is commonly implemented in the state-of-the-art literature, we adopt a feature pretraining step  followed by the episodic meta-training [67] to learn our network. For the k-shot classification task, we initialize the structured FC layer with the average feature map of all support data in each class, and sample a batch of 5 images from the support set to finetune the structured FC layer for 100 iterations.

为了与以前的工作进行公平比较，我们采用了10层ResNet（ResNet10）作为我们的模型主干，这在小样本分类文献中被广泛使用。我们通过移除完全连接的层将其转换为完全卷积的方式。具体而言，给定大小为84×84的图像，该模型生成大小为m5×5×512的特征图，即25512维向量。我们采用GPU加速凸求解器QPTH[1]来解决我们网络中的线性规划问题，并计算反向传播的梯度。正如最新文献中普遍采用的，我们采用特征预训练步骤，然后进行情景元训练[67]来学习我们的网络。对于k-shot分类任务，我们使用每个类中所有支持数据的平均特征图初始化结构化FC层，并从支持集中采样一批5幅图像，以微调结构化FC层100次迭代。

4.2. Dataset Description

We conduct few-shot classification experiments on four popular benchmark datasets: miniImageNet [67], tieredImageNet [49], Fewshot-CIFAR100 (FC100) [43] and Caltech-UCSD Birds-200-2011 (CUB) [68].

我们在四个流行的基准数据集上进行了小样本分类实验：miniImageNet[67]、tieredImageNet[49]、Fewshot-CIFAR100（FC100）[43]和加州理工大学UCSD Birds-200-2011（CUB）[68]。

miniImageNet. miniImageNet was first proposed in [67], and becomes the most popular benchmark in the few-shot classification literature. It contains 100 classes with 600 images in each class, which are built upon the ImageNet dataset [51]. The 100 classes are divided into 64, 16, 20 for meta-training, meta-validation and meta-testing, respectively.
tieredImageNet. tieredImageNet is also a subset of ImageNet, which includes 608 classes from 34 superclasses. Compared with miniImageNet, the splits of metatraining(20), meta-validation(6) and meta-testing(8) are set according to the super-classes to enlarge the domain difference between training and testing phase. The dataset also include more images for training and evaluation (779,165 images in total).
Fewshot-CIFAR100. FC100 is a few-shot classification dataset build on CIFAR100 [23]. We follow the split division proposed in [43], where 36 super-classes were divided into 12 (including 60 classes), 4 (including 20 classes), 4 (including 20 classes), for meta-training, meta-validation and meta-testing, respectively, and each class contains 100 images.
Caltech-UCSD Birds-200-2011. CUB was originally proposed for fine-grained bird classification, which contains 11,788 images from 200 classes. We follow the splits in [72] that 200 classes are divided into 100, 50 and 50 for meta-training, meta-validation and meta-testing, respectively. The challenge in this dataset is the minor difference between classes.

miniImageNet  miniImageNet最早在[67]中提出，并成为小样本分类文献中最流行的基准。它包含100个类，每个类中有600个图像，这些图像是基于ImageNet数据集构建的[51]。100个班级分为64个、16个、20个，分别用于元训练、元验证和元测试。
tieredImageNet  tieredImageNet也是ImageNet的一个子集，它包括来自34个超类的608个类。与miniImageNet相比，元训练（20）、元验证（6）和元测试（8）的拆分是根据超类设置的，以扩大训练和测试阶段的域差异。数据集还包括更多用于培训和评估的图像（总共779165张图像）。
Fewshot-CIFAR100  FC100是基于CIFAR100[23]构建的小样本分类数据集。我们遵循[43]中提出的分割法，其中36个超级类被分为12个（包括60个类）、4个（包括20个类）、4个（包括20个类），分别用于元训练、元验证和元测试，每个类包含100幅图像。
Caltech-UCSD Birds-200-2011  CUB最初被提议用于细粒度鸟类分类，它包含来自200个类别的11788张图像。我们按照[72]中的划分，将200个类分为100、50和50个，分别用于元训练、元验证和元测试。这个数据集中的挑战是类之间的微小差异。

4.3. Ablative Analysis

In our ablation study, we implement various experiments to evaluate the effectiveness of our algorithm. All experiments are conducted on the miniImageNet dataset.

在我们的消融研究中，我们进行了各种实验来评估我们算法的有效性。所有实验均在miniImageNet数据集上进行。

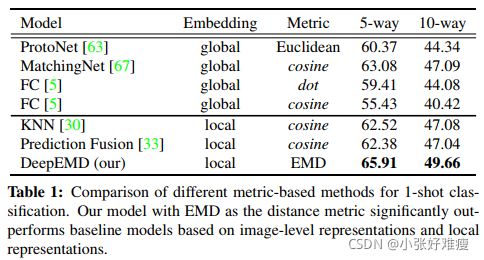
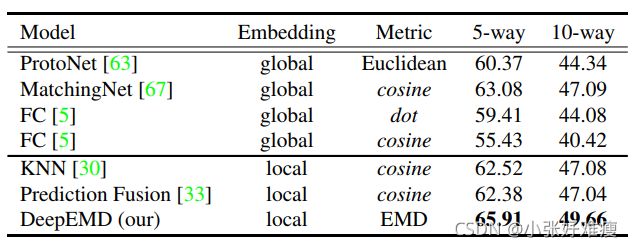
Comparison with methods based on image-level representations. In the beginning, we first compare our method with a set of metric based methods that utilize image-level vector representations on the 1-shot task. These methods adopt global average pooling to generate vector representations for images and use various distance metrics for classification. We select the representative metric-based methods in the literature for comparison: 1) Prototypical Network [63] with Euclidean distance. 2) Matching Network [67] with cosine distance. 3) Finetuning a FC classifier. In [5], Chen et al. propose to fix the pretrained feature extractor and finetune the FC layer with the support images. For fair comparisons, we adopt the same backbones and training schemes for all these baseline methods and report the experiment results in Table. 1. As we can see, our algorithm significantly outperforms baseline methods that relies on image-level vector representations under both 1- shot 5-way and 1-shot 10-way settings, which indicates the effectiveness of the optimal matching based method that relies on local features.

与基于图像级表示的方法进行比较  首先，我们将我们的方法与一组基于度量的方法进行比较，这些方法在1-shot 任务中使用图像级向量表示。这些方法采用全局平均池生成图像的矢量表示，并使用各种距离度量进行分类。我们选择文献中有代表性的基于度量的方法进行比较：1）具有欧氏距离的原型网络[63]。2） 用余弦距离匹配网络[67]。3） 微调FC分类器。在[5]中，Chen等人建议修复预训练特征提取器，并使用支持图像微调FC层。为了公平比较，我们对所有这些基线方法采用相同的主干和训练方案，并在表1中报告实验结果。如我们所见，我们的算法在1- shot 5-way 和 1-shot 10-way设置下显著优于依赖于图像级向量表示的基线方法，这表明了依赖于局部特征的基于最佳匹配的方法的有效性。

Comparison with methods based on local representations. There are also a few methods in the literature focusing on local representations to solve few-shot classification. They all remove the global average pooling in the CNN to achieve dense representations of images. In [30], Li et al. use the top k nearest vectors (KNN) between two feature maps to represent image-level distance. Lifchitz et al. [33] propose to make predictions with each local representation and average their output probabilities. We replace our EMD head with their methods for comparison. The result is shown in Table. 1. Our optimal matching based algorithm outperforms all other model variants. The possible reason is that although the basic ground distance in the EMD is based on local features, our algorithm compares the two structures in a global way. Solely based on nearest local features in two images may not extract sufficient information to differentiate images. For example, eyes can be the nearest feature between animal images, but such feature can mhardly be used to differentiate animal species.

与基于局部表示的方法进行比较   文献中也有一些侧重于局部表示的方法来解决小样本分类问题。它们都删除了CNN中的全局平均池，以实现图像的密集表示。在[30]中，Li等人使用两个特征地图之间的前k个最近向量（KNN）来表示图像级距离。Lifchitz等人[33]建议使用每个局部表示进行预测，并平均其输出概率。我们用他们的方法代替EMD头进行比较。结果如表1所示。我们基于最佳匹配的算法优于所有其他模型变体。可能的原因是，尽管EMD中的基本接地距离基于局部特征，但我们的算法以全局方式比较了这两种结构。仅基于两幅图像中最近的局部特征可能无法提取足够的信息来区分图像。例如，眼睛可以是动物图像之间最接近的特征，但这种特征可以很好地用于区分动物物种。

Weights in the EMD. We next investigate the weights in the EMD formulations. In the earlier work using the EMD for image retrieval, they use the pixel color as the feature and cluster pixels to generate nodes. The weight of the node is set as the portion of pixels in this cluster. We experiment two clustering algorithms to generate weights as the baseline models: K-means [19] and mean-shift [7]. As the clustering process of the mentioned algorithms are non-differentiable, for a fair comparison, we use the features after pre-training to evaluate all methods. We also incorporate a baseline model with equal weights into comparison. To test whether our performance is solely brought by the cross-reference mechanism, we also compare our network with a model variant that is solely based on the crossreference mechanism without EMD. We compute the cosine distance between all vector pairs, and compute a weighted sum of these distances with the node weights generated by the cross-reference mechanism. As we can see from the results in Table. 2, our cross-reference mechanism can bring an improvement of 4.2% over the baseline with equal weights, while clustering-based methods do not help improve the performance, which demonstrates that the number of pixels dose not necessarily indicate the importance in the few-shot scenario. For the model variant solely based on the cross-reference mechanism as an attention, it can only slightly improve the result of simple average operation, while a combination of both the cross-reference mechanism and the EMD can yield a significant performance improvement, which again validates the advantages of using the EMD as the metric and the effectiveness of the crossreference mechanism.

EMD中的权重   接下来，我们将研究EMD公式中的权重。在早期使用EMD进行图像检索的工作中，他们使用像素颜色作为特征，并对像素进行聚类以生成节点。节点的权重设置为该簇中像素的部分。我们实验了两种聚类算法来生成权重作为基线模型：K-means[19]和meanshift[7]。由于上述算法的聚类过程是不可微的，为了公平比较，我们使用预训练后的特征来评估所有方法。我们还将一个具有相同权重的基线模型纳入比较。为了测试我们的性能是否完全是由交叉参考机制带来的，我们还将我们的网络与完全基于交叉参考机制而没有EMD的模型变体进行比较。我们计算所有向量对之间的余弦距离，并使用交叉引用机制生成的节点权重计算这些距离的加权和。从表2中的结果可以看出。我们的交叉参考机制可以在同等权重的情况下比基线提高4.2%，而基于聚类的方法无助于提高性能，这表明像素数量并不一定表明在少数镜头场景中的重要性。对于仅基于交叉参考机制作为注意事项的模型变量，它只能略微改善简单平均操作的结果，而交叉参考机制和EMD的组合可以产生显著的性能改进，这再次验证了使用EMD作为度量的优势和交叉参考机制的有效性。

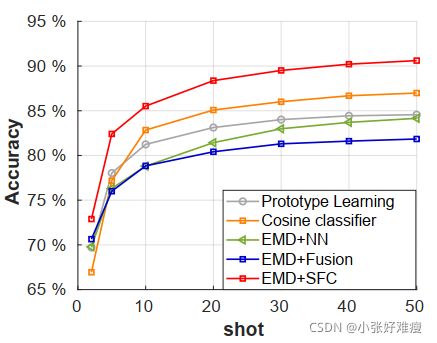
Comparison with other k-shot methods. As the EMD distance metric is a paired function for two structures, the first baseline model for k-shot experiment is the nearest neighbour (NN) method that classifies the query images as the category of the nearest support sample. We also test making prediction with each support sample and fuse their logits. We then compare our network with a few k-shot solutions in previous works: 1) Prototype Learning. In [63], they average the feature embeddings of support images in each class as the prototype and apply the nearest neighbour method for classification. 2) Finetuning a cosine classifier [5]. We test the model performance on the k-shot 5-way tasks under multiple k values , and the results are shown in Fig. 4. Our structured FC layer consistently outperforms baseline models and with the number of support sets increasing, our network shows even more advantages.

与其他k-shot方法的比较  由于EMD距离度量是两种结构的配对函数，k-shot实验的第一个基线模型是最近邻（NN）方法，该方法将查询图像分类为最近支持样本的类别。我们还对每个支持样本进行预测测试，并融合它们的logit。然后，我们将我们的网络与之前工作中的几个k-shot解决方案进行比较：1）原型学习。在[63]中，他们将每个类别中支持图像的特征嵌入平均作为原型，并应用最近邻方法进行分类。2） 微调余弦分类器[5]。我们在多个k值下测试了k-shot五向任务的模型性能，结果如图4所示。我们的结构化FC层始终优于基线模型，随着支持集数量的增加，我们的网络显示出更多的优势。

Figure 4: Experiment on 5-way k-shot classification. The proposed structured FC layer significantly outperforms previous k-shot solutions.  5-way k-shot分类实验。所提出的结构化FC层的性能明显优于以前的k-shot解决方案。 

Visualization of matching flows and weights. It is interesting to visualize the optimal matching flows and node weights in the network inference process. In Fig. 5, we provide some visualization examples. The middle image plots the best matched patch of each local region in the left image,
and the weight controls the brightness of the corresponding region. The middle image can also be seen as a reconstructed version of the left image, using the local patches from the right image. As we can see, our algorithm can establish semantic correspondence between local regions, and the background regions in the left image are given small weight, thus contributing less to the overall distance. The visualization of full matching flows and more examples can be found in our supplementary material.

匹配流和权重的可视化   在网络推理过程中，可视化最佳匹配流和节点权重是一个有趣的问题。在图5中，我们提供了一些可视化示例。中间图像绘制左侧图像中每个局部区域的最佳匹配面片，
权重控制对应区域的亮度。中间图像也可以被视为左图像的重建版本，使用右图像的局部面片。如我们所见，我们的算法可以在局部区域之间建立语义对应，并且左侧图像中的背景区域被赋予较小的权重，因此对整体距离的贡献较小。完整匹配流的可视化和更多示例可在我们的补充材料中找到。

Figure 5: Visualization of the optimal matching flows. Given two images (left and right), we plot the best matched patch of each local region in the left image (middle). The weight controls the brightness of the corresponding region. The middle image can also be seen as the reconstruction of the left image using patches from the right one. Our algorithm can effectively establish semantic correspondence between local regions and gives less weights to the background regions.  最佳匹配流的可视化。给定两幅图像（左侧和右侧），我们在左侧图像（中间）中绘制每个局部区域的最佳匹配面片。权重控制相应区域的亮度。中间的图像也可以看作是使用右图像的面片重建左图像。该算法能够有效地建立局部区域之间的语义对应关系，并且对背景区域赋予较少的权重。

4.4. Cross-Domain Experiments

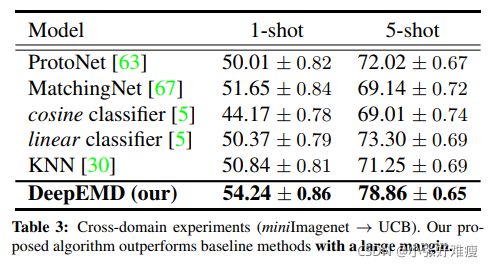
Following the experimental setups in [5], we perform a cross-domain experiment that models are trained on miniImagenet and evaluated on the CUB dataset. Due to the large domain gap, we can better evaluate the the ability to learn transferable knowledge in different algorithms. We compare our proposed method with baseline models in the Table. 3. As we can see, our algorithm outperforms the baseline models with a large margin. This shows that local features can provide more transferable and discriminative information across domains. Moreover, due to our cross-reference mechanism, the optimal matching can be restricted within the co-occurrent object regions that have high feature response, such that the final distance is based on confident regions and representations, and thus has the ability to filter noise when there is a huge domain shift.

按照[5]中的实验设置，我们执行了一个跨域实验，模型在miniImagenet上进行训练，并在CUB数据集上进行评估。由于领域差距较大，我们可以更好地评估不同算法学习可转移知识的能力。我们将我们提出的方法与表中的基线模型进行比较，见表3。正如我们所看到的，我们的算法在很大程度上优于基线模型。这表明，局部特征可以跨域提供更多可传递和区分的信息。此外，由于我们的交叉参考机制，最佳匹配可以限制在具有高特征响应的共现目标区域内，因此最终距离基于置信区域和表示，从而在存在巨大域偏移时具有过滤噪声的能力。

4.5. Time Complexity

Compared with the baseline models, the training and inference of DeepEMD come with more computation cost, as an LP problem must be solved for each forward process. As is discussed in [1], the main computation lies in the factorization of the KKT matrix as well as back-substitution when using the interior point method to solve the LP problem, which have cubic and quadratic time complexity, respectively. We also tried the OpenCV library for solving the LP problem via a modified simplex algorithm, which is much faster than the QPTH [1] solver which uses the interior point method. Therefore, we can use QPTH for training the network and use OpenCV for validation and the final test.

与基线模型相比，DeepEMD的训练和推理需要更多的计算量，因为每个正向过程都必须解决一个LP问题。正如[1]中所讨论的，当使用内点方法解决LP问题时，主要计算在于KKT矩阵的因式分解以及回代，这两种方法分别具有三次和二次时间复杂度。我们还尝试使用OpenCV库通过改进的单纯形算法解决LP问题，这比使用内点法的QPTH[1]解算器快得多。因此，我们可以使用QPTH来训练网络，并使用OpenCV进行验证和最终测试。

4.6. Comparison with the State-of-the-Art

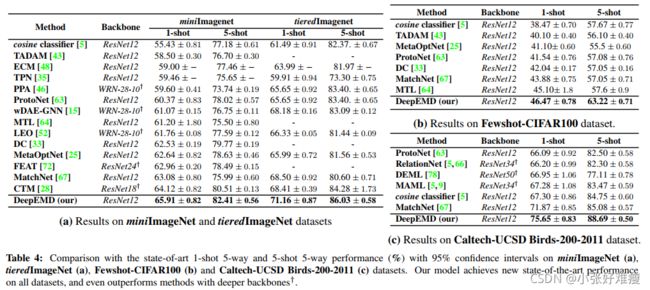
Finally, we compare our algorithm with the state-ofthe-art methods. We report 1-shot 5way and 5-shot 5-way performance on 4 popular benchmarks: miniImageNet, tieredImageNet, FC100 and CUB. We reproduce the models in some earlier works [5, 63, 67] with our network backbone and training strategy, and report the highest performance between our results and their reported ones. The results are shown in Table. 4. Our algorithm achieves new state-of-the-art performance on all datasets. In particular,our results outperform the state-of-the-art performance by a significant margin on multiple tasks, e.g., 1-shot (%3.78) and 5-shot (3.61%) on the CUB dataset; 5-shot (%5.55) on the FC100 dataset.

最后，我们将我们的算法与最先进的方法进行比较。我们在4个流行的基准上报告了1-shot 5way和5-shot 5-way性能：miniImageNet、tieredImageNet、FC100和CUB。我们使用我们的网络主干网和培训策略复制了一些早期工作[5,63,67]中的模型，并报告了我们的结果与其报告结果之间的最高性能。结果如表4所示。我们的算法在所有数据集上都实现了最新的性能。特别是，我们的结果在多个任务上比最先进的性能有显著的优势，例如，CUB数据集上的1次（3.78%）和5次（3.61%）；FC100数据集上的5-shot（%5.55）。

5  结论

We have proposed a few-shot classification framework that employs the Earth Mover’s Distance as the distance metric. The implicit theorem allows our network end-to-end trainable. Our proposed cross-reference mechanism for setting the weights of nodes turns out crucial in the EMD formulation and can effectively minimize the negative impact caused by irrelevant regions. The learnable structured fully connected layer can directly classify dense representations of images in the k-shot settings. Our algorithm achieves new state-of-the-art performance on multiple dataset.

我们提出了一个以Earth Mover’s Distance作为距离度量的小样本分类框架。隐式定理允许我们的网络端到端可训练。我们提出的用于设置节点权重的交叉参考机制在EMD公式中至关重要，并且可以有效地最小化不相关区域造成的负面影响。可学习的结构化完全连接层可以在k-shot设置中直接对图像的密集表示进行分类。我们的算法在多个数据集上实现了最新的性能。