Probabilistic Machine Learning: An Introduction 读书笔记第一章
目录
- 介绍
-
- 1. 机器学习的定义
- 2. 监督学习
-
- 2.1 分类
-
- 2.1.1 模型拟合
- 2.1.2 不确定性
- 2.2 回归
-
- 2.2.1 线性回归
- 2.2.2 多项式回归
- 2.2.3 深度神经网络
- 2.3 过度拟合和泛化
- 2.4 无免费午餐定理
- 3. 无监督学习
-
- 3.1 聚类
- 3.2 自监督学习
- 3.3 评估非监督学习
- 4 强化学习
介绍
1. 机器学习的定义
目前广为接受的定义来自 Tom Mitchell
A computer program is said to learn from experience E with respect to some class of tasks T, and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
本书从概率的视角看待机器学习，使用概率方法的原因有两个：
- 不确定条件下的最优决策方法
- 概率建模是大多数其他科学和工程领域所使用的语言，从而提供了这些领域之间的统一框架
2. 监督学习
定义：任务 T T T 学习从输入 x ∈ X x \in X x∈X 到输出 y ∈ Y y \in Y y∈Y 的映射 f f f
x x x 称为特征、协变量或预测因子，通常是一个固定的数字维度向量。
y y y 也称为标签、目标或响应。
2.1 分类
在分类问题中，输出空间是一组称为类的 C C C 无序且互斥的标签， Y = { 1 , 2 , 3... , C } Y=\lbrace 1,2,3...,C \rbrace Y={1,2,3...,C}
监督学习的目标：自动提出分类模型，以便可靠地预测任何给定输入的标签
假设我们有一组分类器：
f ( x ; θ ) f(\mathbf{x}; \pmb {\theta}) f(x;θθθ)
其中 θ \pmb{\theta} θθθ 为分类器中的参数
2.1.1 模型拟合
误分类率用于衡量性能，定义：
其中的二元指标函数 (binary indicator function) 定义：
以上的二元指标函数用于每种错误权重相同的情况。在错误的权重不同的情况下，需要使用损失函数 (loss function)： ℓ ( y , y ^ ) \ell(y,\hat y) ℓ(y,y^)
因此可以定义经验风险 (empirical risk) 去衡量预测器的平均损失：
至此我们可以定义模型拟合的一种方法是找到一组参数，最小化训练集上的经验风险，称作经验风险最小化 (empirical risk minimization)：
2.1.2 不确定性
在大多数情况下，对给定的输入我们不能完美地预测确切的输出
原因：
- 由于缺乏输入-输出映射的知识（认知不确定性或模型不确定性）
- 和/或由于映射中固有的(不可约的)随机性(偶然不确定性或数据不确定性)
我们可以使用条件概率来捕获不确定性：
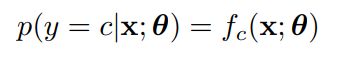
表示不确定性对某些应用来说是很重要的，比如我们不能确定预测的鸢尾花是否可以吃时，我们最好不要吃。
拟合概率模型时，常用负对数概率作为损失函数： 
这更符合直觉：一个好的模型(低损耗)是一个为每个对应的输入 x x x 分配一个大概率输出真实的 y y y 的模型
因此在训练集上有负对数似然：
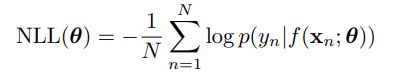
如果我们把它最小化，就有最大似然估计：
2.2 回归
定义：预测一个实数 y ∈ R y \in \mathbb{R} y∈R
常用损失函数：平方损失 ( ℓ 2 \ell_2 ℓ2 loss)
ℓ 2 ( y , y ^ ) = ( y − y ^ ) 2 \ell _2 (y, \hat y) = (y - \hat y)^2 ℓ2(y,y^)=(y−y^)2
基于平方损失我们可以定义均方差 (mean squared error)：
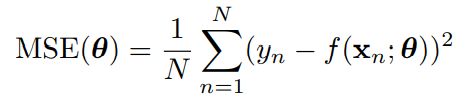
基于上述对不确定性的讨论，我们需要对不确定性建模。在回归问题中，我们通常假设输入是正态分布，定义为：
其中：
- μ \mu μ：输入的均值
- σ 2 \sigma^2 σ2：方差
- 2 π σ 2 \sqrt{2\pi \sigma^2} 2πσ2：确保密度积分为1所需的归一化常数
因此我们获得条件概率分布：
假设我们考虑简单的情况， σ \sigma σ 固定，那么有相应的负对数似然：
因此，计算最大似然估计的参数将导致最小化的平方误差。
2.2.1 线性回归
一元线性回归：
f ( x ; θ ) = w x + b f(x; \pmb{\theta}) = wx + b f(x;θθθ)=wx+b
其中， θ = （ w , b ) \theta = （w,b) θ=（w,b) 是模型的所有所有参数。
在拟合模型的过程中，我们需要不断调整 θ \theta θ 来最小化平方误差，直到我们找到最小二乘解：
θ ^ = a r g m i n θ MSE ( θ ) \pmb{\hat \theta} = {\mathop{argmin}\limits_\theta} \, \text{MSE}(\pmb\theta) θ^θ^θ^=θargminMSE(θθθ)
假设我们有多个输入的情况（多个 x x x）
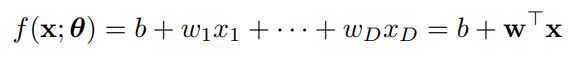
为了避免符号混乱，我们通过定义 w ~ = [ b , w 1 , … , w D ] \tilde{\mathbf{w}}= [b,w_1,\dots,w_D] w~=[b,w1,…,wD] 和 x ~ = [ 1 , x 1 , … , x D ] \tilde\mathbf{x} = [1,x_1, \dots ,x_D] x~=[1,x1,…,xD] 来将偏差项b吸收到权重中，所以：
w ~ T x ~ = w T x + b \tilde{\mathbf{w}}^\mathsf{T}\tilde\mathbf{x} = {\mathbf{w}}^\mathsf{T} \mathbf{x} + b w~Tx~=wTx+b
因此我们可以将仿射函数转化成线性函数：
f ( x ; w ) = w T x f(\mathbf{x};\mathbf{w}) = {\mathbf{w}}^\mathsf{T} \mathbf{x} f(x;w)=wTx
- 统计学中， w \mathbf{w} w 称为回归系数， b b b 称为斜率
- 机器学习中， w \mathbf{w} w 称为权重， b b b 称为偏差
2.2.2 多项式回归
形式：
f ( x ; w ) = w T ϕ ( x ) f(x;\mathbf{w})={\mathbf{w}}^\mathsf{T} \phi(x) f(x;w)=wTϕ(x)
ϕ ( x ) \phi(x) ϕ(x) 是从输入中获得的特征向量
ϕ ( x ) = [ 1 , x , x 2 , … , x D ] \phi(x)=[1,x,x^2,\dots,x^D] ϕ(x)=[1,x,x2,…,xD]
当 D = N − 1 D=N-1 D=N−1 时，每个数据点有一个参数
我们还可以将多项式回归应用到多维输入的情况，比如：
注意，上述模型仍然使用参数 w \mathbf{w} w 的线性函数的预测函数，即使它是原始输入 x \mathbf {x} x 的非线性函数。因为线性模型可推导出具有唯一全局最优的 MSE \text {MSE} MSE 损失函数。
2.2.3 深度神经网络
在手动指定 ϕ ( x ) = [ 1 , x , x 2 , … , x D ] \phi(\mathbf{x}) = [1,x,x^2,\dots,x^D] ϕ(x)=[1,x,x2,…,xD] 的基础上，我们可以通过学习自动地非线性特征提取创建更强大的模型。
令 V \mathbf{V} V 为 ϕ ( x ) \phi(\mathbf{x}) ϕ(x) 拥有的参数集，构造模型：
再递归地分解特征提取器 ϕ ( x ; V ) \phi(\mathbf x;\mathbf{V}) ϕ(x;V) 成更简单的函数组合，获得 L L L 嵌套函数的堆栈
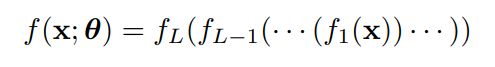
其中 f ℓ ( x ) = f ( x ; θ ℓ ) f_{\ell}(\mathbf x) = f(\mathbf x; \pmb \theta_\ell) fℓ(x)=f(x;θθθℓ) 是层 (layer) ℓ \ell ℓ 上的函数
最后一层 f L ( x ) = w T f 1 : L − 1 ( x ) f_L(\mathbf x)=\mathbf w ^ \mathsf{T} f_{1:L-1}(\mathbf x) fL(x)=wTf1:L−1(x) 是学习的线性特征提取器
2.3 过度拟合和泛化
重写经验风险我们可以得到三种风险度量函数：
-
训练集风险
这种形式可以明确表示正在评估损失的数据集 -
总体风险
为了检测模型是否过拟合，我们假设(目前)可以访问用于生成训练集的真实(但未知)分布，因此获得总体风险公式 -
测试集风险
在实践中，我们不知道 p ∗ p^∗ p∗。然而，我们可以将数据划分为两个子集，即训练集和测试集。然后我们可以用测试风险来近似群体风险
通过一个适当灵活的模型，我们可以将训练损失降到零(假设没有标签噪声)，只需记住每个输入的正确输出。但我们关心的是对新数据的预测精度，这可能不是训练集的一部分。一个完美地拟合训练数据，但太复杂的模型，被认为是遭受过拟合。
2.4 无免费午餐定理
All models are wrong, but some models are useful. — George Box
没有一个最佳模型能最优地解决所有类型的问题，因此选择模型的方法最好基于领域知识，以及不断地试错
3. 无监督学习
定义：给定一群输入
D = { x n : n = 1 : N } \mathcal D = \{ \mathbf x_n : n=1:N\} D={xn:n=1:N}
而没有对应的输出 y n \mathbf y_n yn
从概率的角度来看，我们可以把无监督学习任务看作是拟合一个无条件模型的形式 p ( x ) p (\mathbf x) p(x)，它可以生成新的数据 x \mathbf x x
无监督学习的优势：
- 避免收集大量的被标注数据（标注数据浪费大量时间且昂贵）
- 避免学习如何将世界划分为任意类别的需要
- 能够“解释”高维的输入
3.1 聚类
目标：将输入划分为包含“相似”点的区域
注意，没有正确的集群数量;相反，我们需要考虑模型复杂性和适合数据之间的权衡
从未标记的数据中创建代理监督任务
3.2 自监督学习
定义：从未标记的数据中创建代理监督任务
希望是由此产生的预测
x ^ 1 = f ( x 2 ; θ ) \mathbf {\hat x_1} = f (\mathbf x_2; \pmb \theta) x^1=f(x2;θθθ)，其中 x 2 \mathbf x_2 x2 是观测的输入， x ^ 1 \mathbf {\hat x_1} x^1 是预测的输出，将从数据中学习有用的特征，然后用于标准的下游监督任务
3.3 评估非监督学习
很难评估无监督学习方法的输出质量，因为没有可以与之比较的基本事实
常用方法：测量模型分配给看不见的测试实例的概率，我们可以通过数据的负对数似然估计
而负对数似然估计要求我们知道输入的分布函数，因此无监督学习的问题转化为密度估计。其理念是，一个好的模型不会被实际数据样本“惊讶”(即，将赋予它们高概率)。
然而，密度估计是困难的。此外，将高概率赋值给数据的模型可能不会学到有用的高级模式(毕竟，该模型只能记住所有的训练例子)。
另一个评价指标是使用学习的无监督表示作为特征或输入下游监督学习方法
如果无监督方法发现了有用的模式，那么使用这些模式来执行监督学习应该是可能的，使用的标签数据比使用原始特征时少得多。类似特征降维，用更少的特征表示数据，换个角度来说，这提高了样本效率。
提高样本效率是一个有用的评价指标，但在许多应用中，特别是在科学领域，无监督学习的目标是 “获得理解” ，而不是提高某些预测任务的表现。因此我们要求使用的模型具有可解释性，但同时也能接受数据中的学习到的模式。
4 强化学习
理解：系统或代理 (agent) 必须学会如何与环境交互，这可以通过策略 a = π ( x ) \mathbf a=\pi(\mathbf x) a=π(x) 进行编码，指定对每个可能输入的 x \mathbf x x （来自环境状态）采取何种操作。系统只偶尔接收奖励（或惩罚）信号回应采取行动。
强化学习具有广泛的适用性，但是比监督学习和无监督学习更难发挥作用。因为奖励信号偶尔出现（就算代理最终达到我们的期望行为），而且代理也无法清楚具体哪个行为时获得奖励的原因。