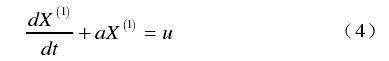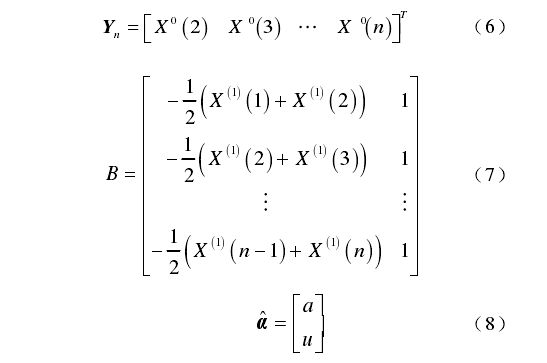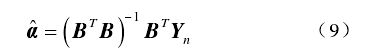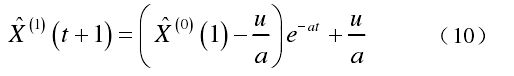灰度预测模型_python

灰色预测法

灰色预测模型是通过少量的、不完全的信息，建立数学模型并做出预测的一种预测方法。是处理小样本（4个就可以）预测问题的有效工具，而对于小样本预测问题回归和神经网络的效果都不太理想。

最简单的模型是GM(1,1)，G：Grey（灰色）；M：模型；(1,1)：只含有一个变量的一阶微分方程模型。

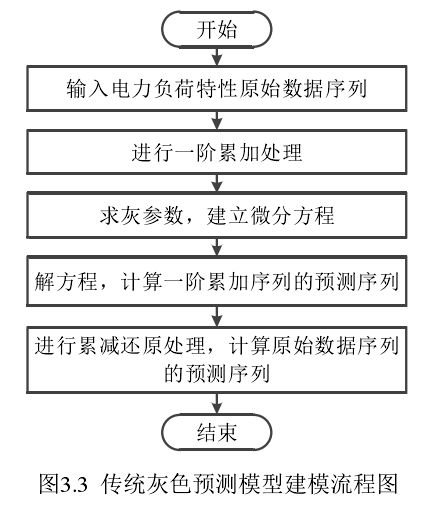
算法

（1）输入原始电力负荷特性数据序列$X^{(0)}$判断是否适用GM（1,1）。 定义覆盖区间$\Theta =(e^{\frac{-2}{k+1}},e^{\frac{2}{k+2}})$​

定义$\lambda (n)=\frac{x(n-1)}{x(n)},n=2,3,...,k$，若满足对任意n，有$\lambda (n)\in \Theta ,k=2,3,4,...,k$，则我们称$X^{(0)}$是 可以作为GM(1,1)的数据而被灰度预测的。

（2）对原始数据集合$X^{(0)}$​进行分布特征检验以后，采用累加器进行累加数据生成，获取新的数据序列如式

（3）将新的数据序列$X^{(1)}$​ 表示为一阶微分方程的形式，如式（4）

​ 其中a 为模型的发展灰数，u 是内生控制参量。

（4）求解模型。计算结果为

​ 其中，

​ 基于最小二乘算法的估计结果为

（5）进而可以将模型的相应时间函数表示为

（6）${\hat{X}}^{(1)}(t+1)$​为最终预测值，其递归分析为。

$${\hat{X}}^{(0)}(t+1)={\hat{X}}^{(1)}(t+1)-{\hat{X}}^{(1)}(t)$$

（7）通过后验差比评估模型效果，该值为残差方差 / 数据方差；其用于衡量模型的拟合精度情况，C值越小越好，一般小于0.65即可。。

案例及代码

以江苏省无锡市锡北镇电力负荷预测为例，给出灰度预测的结果

年份	1995	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014
最大负荷（kw）	21.2	22.7	24.36	26.22	28.18	30.16	32.34	34.72	37.3	40.34	44.08	47.92	51.96	56.02	60.14	64.58	68.92	73.36	78.98	86.6

• 原始数据

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']  # 步骤一（替换sans-serif字体）
plt.rcParams['axes.unicode_minus'] = False  # 步骤二（解决坐标轴负数的负号显示问题）

# 原始数据X
X=[21.2, 22.7, 24.36, 26.22, 28.18, 30.16, 32.34, 34.72, 37.3, 40.34,44.08, 47.92, 51.96, 56.02, 60.14, 64.58, 68.92, 73.36, 78.98, 86.6]
# 训练集
X0 = np.array([21.2, 22.7, 24.36, 26.22, 28.18, 30.16, 32.34, 34.72, 37.3, 40.34])

# 测试集
X_test =[44.08, 47.92, 51.96, 56.02, 60.14, 64.58, 68.92, 73.36, 78.98, 86.6]

# 分布特征检验
## 计算级比
lens = len(X0)
lambds = [X0[i-1]/X0[i] for i in range(1, lens)]
## 计算区间
X_min = np.e**(-2/(lens+1))
X_max = np.e**(2/(lens+1))
## 检验
is_ok = True
for lambd in lambds:
    if (lambd < X_min or lambd > X_max):
        is_ok = False
if (is_ok == False):
    print('该数据未通过检验')
else:
    print('该数据通过检验')
    
#  一阶累加XR1
X1=X0.cumsum()
print("一阶累加序列X1:",X1)

# 预测模型背景值
L = (np.array([-0.5*(X1[k-1]+X1[k]) for k in range(1,len(X1))])).reshape(len(X1)-1,1)
# 数据矩阵Y_n、B
Y_n = (X0[1:]).reshape(len(L),1)
B =np.hstack((L,np.ones(len(L)).reshape(len(L),1)))
# 求灰参数
a,u = np.linalg.inv(np.matmul(B.T, B)).dot(B.T).dot(Y_n)
print("灰参数a：",a,"，灰参数u：",u)

# 构建XR1的微分方程，并求解XR1,XR1为预测序列
def get_predict(init,u,a,k):
    pred = (init-u/a)*np.exp(-a*(k-1))+u/a
    return pred[0]

X1_hat = [get_predict(X0[0],u,a,k) for k in range(1,len(X1)+1)]
print(X1_hat)
X0_hat = np.diff(X1_hat)

X0_hat = np.hstack((X1_hat[0],X0_hat))
print(X0_hat)
plt.grid()
plt.plot(np.arange(len(X0)), X0, '->')
plt.plot(np.arange(len(X0)), X0_hat, '-o')
plt.legend(['负荷实际值','灰色预测模型预测值'])
plt.show()

# 评估指标
S1 = np.var(X0_hat) # 预测结果方差
S2 = np.var(X0-X0_hat)# 残差方差
C = S2/S1 # 后验差
## 结果
if (C <= 0.35):
    print('1级，效果好')
elif (C <= 0.5 and C >= 0.35):
    print('2级，效果合格')
elif (C <= 0.65 and C >= 0.5):
    print('3级，效果勉强')
else:
    print('4级，效果不合格')
    
    
# 测试集
X1_test_hat = [get_predict(X0[0],u,a,k) for k in range(1,len(X0)+len(X_test)+1)]
X0_test_hat = np.diff(X1_test_hat)
X0_test_hat = np.hstack((X1_test_hat[0],X0_test_hat))
plt.grid()
plt.plot(np.arange(len(X_test)), X_test, '->')
plt.plot(np.arange(len(X_test)), X0_test_hat[len(X0):], '-o')
plt.legend(['负荷实际值','灰色预测模型预测值'])
plt.title('测试集')
plt.show()

• 训练集

  

• 测试集结果