TensorFlow 2.0深度学习算法实战教材---第11章 循环神经网络

人工智能的强力崛起，可能是人类历史上最好的事情，也可能是最糟糕的事情。−史蒂芬•霍金

卷积神经网络利用数据的局部相关性和权值共享的思想大大减少了网络的参数量，非常适合于图片这种具有空间(Spatial)局部相关性的数据，已经被成功地应用到计算机视觉领域的一系列任务上。自然界的信号除了具有空间维度之外，还有一个时间(Temporal)维度。具有时间维度的信号非常常见，比如我们正在阅读的文本、说话时发出的语音信号、随着时间变化的股市参数等。这类数据并不一定具有局部相关性，同时数据在时间维度上的长度也是可变的，卷积神经网络并不擅长处理此类数据。

那么如何解决这一类信号的分析、识别等问题是将人工智能推向通用人工智能路上必须解决的一项任务。本章将要介绍的循环神经网络可以较好地解决此类问题。在介绍循环神经网络之前，首先我们来介绍对于具有时间先后顺序的数据的表示方法。

11.1 序列表示方法

具有先后顺序的数据一般叫作序列(Sequence)，比如随时间而变化的商品价格数据就是非常典型的序列。考虑某件商品 A 在 1 月到 6 月之间的价格变化趋势，我们记为一维向量：[1, 2, 3, 4, 5, 6]，它的 shape 为[6]。如果要表示件商品在 1 月到 6 月之间的价格变化趋势，可以记为 2 维张量：
$$\left[\left[x_1^{(1)},x_2^{(1)},\cdots ,x_6^{(1)}\right],\left[x_1^{(2)},x_2^{(2)},\cdots ,x_6^{(2)}\right],\cdots ,\left[x_1^{(b)},x_2^{(b)},\cdots ,x_6^{(b)}\right]\right]$$
其中表示商品的数量，张量 shape 为[, 6]。

这么看来，序列信号表示起来并不麻烦，只需要一个 shape 为[, ]的张量即可，其中为序列数量，为序列长度。但是对于很多信号并不能直接用一个标量数值表示，比如每个时间戳产生长度为的特征向量，则需要 shape 为[, , ]的张量才能表示。考虑更复杂的文本数据：句子。它在每个时间戳上面产生的单词是一个字符，并不是数值，不能直接用某个标量表示。我们已经知道神经网络本质上是一系列的矩阵相乘、相加等数学运算，它并不能够直接处理字符串类型的数据。如果希望神经网络能够用于自然语言处理任务，那么怎么把单词或字符转化为数值就变得尤为关键。接下来我们主要探讨文本序列的表示方法，其他非数值类型的信号可以参考文本序列的表示方法。

对于一个含有个单词的句子，单词的一种简单表示方法就是前面我们介绍的 One-hot编码。以英文句子为例，假设我们只考虑最常用的 1 万个单词，那么每个单词就可以表示为某位为 1，其它位置为 0 且长度为 1 万的稀疏 One-hot 向量；对于中文句子，如果也只考虑最常用的 5000 个汉字，同样的方法，一个汉字可以用长度为 5000 的 One-hot 向量表示。如图 11.1 中所示，如果只考虑个地名单词，可以将每个地名编码为长度为的 Onehot 向量。

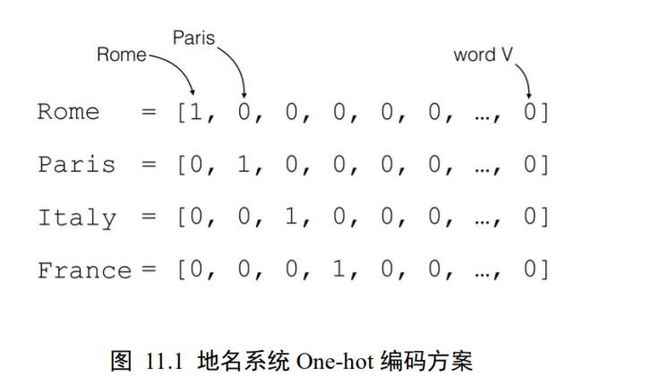
我们把文字编码为数值的过程叫作 Word Embedding。One-hot 的编码方式实现 WordEmbedding 简单直观，编码过程不需要学习和训练。但是 One-hot 编码的向量是高维度而且极其稀疏的，大量的位置为 0，计算效率较低，同时也不利于神经网络的训练。从语义角度来讲，One-hot 编码还有一个严重的问题，它忽略了单词先天具有的语义相关性。举个例子，对于单词“like”、“dislike”、“Rome”、“Paris”来说，“like”和“dislike”在语义角度就强相关，它们都表示喜欢的程度；“Rome”和“Paris”同样也是强相关，他们都表示欧洲的两个地点。对于一组这样的单词来说，如果采用 One-hot 编码，得到的向量之间没有相关性，不能很好地体现原有文字的语义相关度，因此 One-hot 编码具有明显的缺陷。

在自然语言处理领域，有专门的一个研究方向在探索如何学习到单词的表示向量(Word Vector)，使得语义层面的相关性能够很好地通过 Word Vector 体现出来。一个衡量词向量之间相关度的方法就是余弦相关度(Cosine similarity)：
$$\text{ similarity }(\mathbf{a},\mathbf{b})\triangleq \cos (\theta )=\frac{\mathbf{a}\cdot \mathbf{b}}{|\mathbf{a}|\cdot |\mathbf{b}|}$$
其中和代表了两个词向量。图 11.2 演示了单词“France”和“Italy”的相似度，以及单词“ball”和“crocodile”的相似度，为两个词向量之间的夹角。可以看到cos()较好地反映了语义相关性。

11.1.1 Embedding 层

在神经网络中，单词的表示向量可以直接通过训练的方式得到，我们把单词的表示层叫 Embedding 层。Embedding 层负责把单词编码为某个词向量，它接受的是采用数字编码的单词编号，如 2 表示“I”，3 表示“me”等，系统总单词数量记为$N_{vocab}$，输出长度为$n$的向量：
$$\mathbf{v}=f_{\theta }\left(i|N_{\text{vocab }},n\right)$$
Embedding 层实现起来非常简单，构建一个 shape 为[$N_{vocab}$, ]的查询表对象 table，对于任意的单词编号，只需要查询到对应位置上的向量并返回即可：
$$v=\mathrm{table}[i]$$
Embedding 层是可训练的，它可放置在神经网络之前，完成单词到向量的转换，得到的表示向量可以继续通过神经网络完成后续任务，并计算误差ℒ，采用梯度下降算法来实现端到端(end-to-end)的训练。

在 TensorFlow 中，可以通过layers.Embedding($N_{vocab}$,)来定义一个 Word Embedding层，其中$N_{vocab}$参数指定词汇数量，指定单词向量的长度。例如：

import tensorflow as tf
from tensorflow.keras import layers

x=tf.range(10)#生成10个单词的数字编码
x=tf.random.shuffle(x)#打散
#创建10个单词，每个单词用长度为4的向量表示的层
net=layers.Embedding(10,4)
out=net(x)#获取词向量
print(out)

上述代码创建了 10 个单词的 Embedding 层，每个单词用长度为 4 的向量表示，可以传入数字编码为 0~9 的输入，得到这10个单词的词向量，这些词向量随机初始化的，尚未经过网络训练，例如：

<tf.Tensor: id=96, shape=(10, 4), dtype=float32, numpy=
array([[-0.00998075, -0.04006485, 0.03493755, 0.03328368],
 [-0.04139598, -0.02630153, -0.01353856, 0.02804044],…

我们可以直接查看 Embedding 层内部的查询表 table：

net.embeddings

<tf.Variable 'embedding_4/embeddings:0' shape=(10, 4) dtype=float32, numpy=
array([[ 0.04112223, 0.01824595, -0.01841902, 0.00482471],
 [-0.00428962, -0.03172196, -0.04929272, 0.04603403],…

并查看 net.embeddings 张量的可优化属性为 True，即可以通过梯度下降算法优化。

net.embeddings.trainable
True

11.1.2 预训练的词向量

Embedding 层的查询表是随机初始化的，需要从零开始训练。实际上，我们可以使用预训练的 Word Embedding 模型来得到单词的表示方法，基于预训练模型的词向量相当于迁移了整个语义空间的知识，往往能得到更好的性能。

目前应用的比较广泛的预训练模型有 Word2Vec 和 GloVe 等。它们已经在海量语料库训练得到了较好的词向量表示方法，并可以直接导出学习到的词向量表，方便迁移到其它任务。比如 GloVe 模型 GloVe.6B.50d，词汇量为 40 万，每个单词使用长度为 50 的向量表示，用户只需要下载对应的模型文件即可，“glove6b50dtxt.zip”模型文件约 69MB。

那么如何使用这些预训练的词向量模型来帮助提升 NLP 任务的性能？非常简单，对于Embedding 层，不再采用随机初始化的方式，而是利用我们已经预训练好的模型参数去初始化 Embedding 层的查询表。例如：

#从预训练模型中加载词向量表
embed_glove=load_embed('glove_6B.50d.txt')
#直接利用预训练的词向量表初始化Embedding层
net.set_weights([embed_glove])

经过预训练的词向量模型初始化的 Embedding 层可以设置为不参与训练：net.trainable= False，那么预训练的词向量就直接应用到此特定任务上；如果希望能够学到区别于预训练词向量模型不同的表示方法，那么可以把 Embedding 层包含进反向传播算法中去，利用梯度下降来微调单词表示方法。

11.2 循环神经网络

现在我们来考虑如何处理序列信号，以文本序列为例，考虑一个句子：

“I hate this boring movie”

通过 Embedding 层，可以将它转换为 shape 为[, , ]的张量，为句子数量，为句子长度，为词向量长度。上述句子可以表示为 shape 为[1,5,10]的张量，其中 5 代表句子单词长度，10 表示词向量长度。

接下来逐步探索能够处理序列信号的网络模型，为了便于表达，我们以情感分类任务为例，如图 11.3 所示。情感分类任务通过分析给出的文本序列，提炼出文本数据表达的整体语义特征，从而预测输入文本的情感类型：正面评价或者负面评价。

从分类角度来看，情感分类问题就是一个简单的二分类问题，与图片分类不一样的是，由于输入是文本序列，传统的卷积神经网络并不能取得很好的效果。那么什么类型的网络擅长处理序列数据呢？

11.2.1 全连接层可行吗

首先我们想到的是，对于每个词向量，分别使用一个全连接层网络
$$\mathbf{o}=\sigma \left({\mathbf{W}}_t{\mathbf{x}}_t+{\mathbf{b}}_t\right)$$
提取语义特征，如图 11.4 所示，各个单词的词向量通过个全连接层分类网络1 提取每个单词的特征，所有单词的特征最后合并，并通过分类网络 2 输出序列的类别概率分布，对于长度为的句子来说，至少需要个全网络层。

这种方案的缺点有：

❑ 网络参数量是相当可观的，内存占用和计算代价较高，同时由于每个序列的长度并不相同，网络结构是动态变化的

❑ 每个全连接层子网络和只能感受当前词向量的输入，并不能感知之前和之后的语境信息，导致句子整体语义的缺失，每个子网络只能根据自己的输入来提取高层特征，有如管中窥豹.

我们接下来逐一解决这 2 大缺陷。

11.2.2 共享权值

在介绍卷积神经网络时，我们就比较过，卷积神经网络之所以在处理局部相关数据时优于全连接网络，是因为它充分利用了权值共享的思想，大大减少了网络的参数量，使得网络训练起来更加高效。那么，我们在处理序列信号的问题上，能否借鉴权值共享的思想呢？

图 11.4 中的方案，个全连接层的网络并没有实现权值同享。我们尝试将这个网络层参数共享，这样其实相当于使用一个全连接网络来提取所有单词的特征信息，如图 11.5 所示。

通过权值共享后，参数量大大减少，网络训练变得更加稳定高效。但是，这种网络结构并没有考虑序列之间的先后顺序，将词向量打乱次序仍然能获得相同的输出，无法获取有效的全局语义信息。

11.2.3 全局语义

如何赋予网络提取整体语义特征的能力呢？或者说，如何让网络能够按序提取词向量的语义信息，并累积成整个句子的全局语义信息呢？我们想到了内存(Memory)机制。如果网络能够提供一个单独的内存变量，每次提取词向量的特征并刷新内存变量，直至最后一个输入完成，此时的内存变量即存储了所有序列的语义特征，并且由于输入序列之间的先后顺序，使得内存变量内容与序列顺序紧密关联。

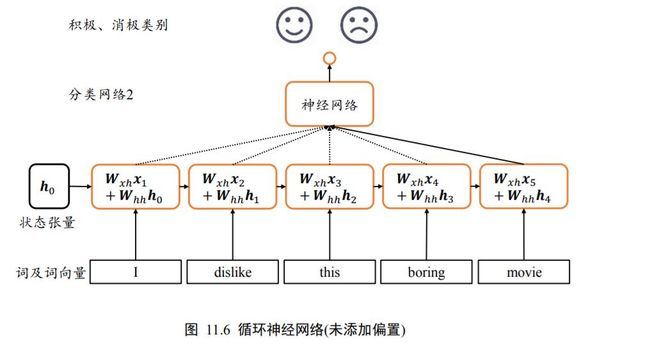
我们将上述 Memory 机制实现为一个状态张量 ，如图 11.6 所示，除了原来的$W_{xh}$参数共享外，这里额外增加了一个$w_{hh}$参数，每个时间戳上状态张量$h$刷新机制为：
$${\mathbf{h}}_t=\sigma \left({\mathbf{W}}_{xh}{\mathbf{x}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1}+\mathbf{b}\right)$$
其中状态张量 $h_0$为初始的内存状态，可以初始化为全 0，经过个词向量的输入后得到网络最终的状态张量 $h_s$， $h_s$较好地代表了句子的全局语义信息，基于$h_s$通过某个全连接层分类器即可完成情感分类任务。

11.2.4 循环神经网络

通过一步步地探索，我们最终提出了一种“新型”的网络结构，如图 11.7 所示，在每个时间戳，网络层接受当前时间戳的输入和上一个时间戳的网络状态向量 −1，经过
$${\mathbf{h}}_t=f_{\theta }\left({\mathbf{h}}_{t-1},{\mathbf{x}}_t\right)$$
变换后得到当前时间戳的新状态向量 ，并写入内存状态中，其中代表了网络的运算逻辑，为网络参数集。在每个时间戳上，网络层均有输出产生，${\mathbf{o}}_t=g_{\varphi }\left({\mathbf{h}}_t\right)$，即将网络的状态向量变换后输出。

上述网络结构在时间戳上折叠，如图 11.8 所示，网络循环接受序列的每个特征向量$x_t$，并刷新内部状态向量$h_t$，同时形成输出$o_t$。对于这种网络结构，我们把它叫做循环网络结构(Recurrent Neural Network，简称 RNN)。

更特别地，如果使用张量$W_{xh}$ 、$W_{hh}$ 和偏置来参数化$f_{\theta }$网络，并按照
$${\mathbf{h}}_t=\sigma \left({\mathbf{W}}_{xh}{\mathbf{x}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1}+\mathbf{b}\right)$$
方式更新内存状态，我们把这种网络叫做基本的循环神经网络，如无特别说明，一般说的循环神经网络即指这种实现。在循环神经网络中，激活函数更多地采用 tanh 函数，并且可以选择不使用偏执来进一步减少参数量。状态向量$h_t$可以直接用作输出，即$o_t$ =$h_t$，也可以对$h_t$做一个简单的线性变换$o_t=W_{ho}\ast h_t$后得到每个时间戳上的网络输出$o_t$。

11.3 梯度传播

通过循环神经网络的更新表达式可以看出输出对张量$W_{xh}$ 、$W_{hh}$ 和偏置均是可导的，可以利用自动梯度算法来求解网络的梯度。此处我们仅简单地推导一下 RNN 的梯度传播公式，并观察其特点。

考虑梯度$\frac{\partial \mathcal{L}}{\partial W_{hh}}$，其中ℒ为网络的误差，只考虑最后一个时刻的输出$o_t$与真实值之间的差距。由于$W_{hh}$ 被每个时间戳上权值共享，在计算$\frac{\partial \mathcal{L}}{\partial W_{hh}}$时需要将每个中间时间戳上面的梯度求和，利用链式法则展开为
$$\frac{\partial \mathcal{L}}{\partial W_{hh}}=\sum _{i=1}^t\frac{\partial \mathcal{L}}{\partial {\mathbf{o}}_t}\frac{\partial {\mathbf{o}}_t}{\partial {\mathbf{h}}_t}\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}\frac{{\partial }^{+}{\mathbf{h}}_i}{\partial {\mathbf{W}}_{hh}}$$
其中$\frac{\partial \mathcal{L}}{\partial {\mathbf{o}}_t}$可以基于损失函数直接求得，$\frac{\partial {\mathbf{o}}_t}{\partial {\mathbf{h}}_t}$在$o_t=h_t$的情况下：
$$\frac{\partial {\mathbf{o}}_t}{\partial {\mathbf{h}}_t}=I$$
而$\frac{{\partial }^{+}{\mathbf{h}}_i}{\partial W_{hh}}$的梯度将$h_i$展开后也可以求得：
$$\frac{{\partial }^{+}{\mathbf{h}}_i}{\partial {\mathbf{W}}_{hh}}=\frac{\partial \sigma \left({\mathbf{W}}_{xh}{\mathbf{x}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1}+\mathbf{b}\right)}{\partial {\mathbf{W}}_{hh}}$$

其中$\frac{{\partial }^{+}{\mathbf{h}}_i}{\partial W_{hh}}$只考虑到一个时间戳的梯度传播，即“直接”偏导数，与$\frac{\partial \mathcal{L}}{\partial W_{hh}}$考虑 = 1, ⋯ ,所有的时间戳的偏导数不同。

因此，只需要推导出$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}$的表达式即可完成循环神经网络的梯度推导。利用链式法则，我们把$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}$分拆分连续时间戳的梯度表达式：
$$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}=\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_{t-1}}\frac{\partial {\mathbf{h}}_{t-1}}{\partial {\mathbf{h}}_{t-2}}\dots \frac{\partial {\mathbf{h}}_{i+1}}{\partial {\mathbf{h}}_i}=\prod _{k=i}^{t-1}\frac{\partial {\mathbf{h}}_{k+1}}{\partial {\mathbf{h}}_k}$$
考虑
$${\mathbf{h}}_{k+1}=\sigma \left({\mathbf{W}}_{xh}{\mathbf{x}}_{k+1}+{\mathbf{W}}_{hh}{\mathbf{h}}_k+\mathbf{b}\right)$$
那么
$$\begin{array}{c}\frac{\partial {\mathbf{h}}_{k+1}}{\partial {\mathbf{h}}_k}={\mathbf{W}}_{hh}^T\mathrm{diag}\left({\sigma }^{\prime }\left({\mathbf{W}}_{xh}{\mathbf{x}}_{k+1}+{\mathbf{W}}_{hh}{\mathbf{h}}_k+\mathbf{b}\right)\right)\\ ={\mathbf{W}}_{hh}^T\mathrm{diag}\left({\sigma }^{\prime }\left({\mathbf{h}}_{k+1}\right)\right)\end{array}$$
其中()把向量 x 的每个元素作为矩阵的对角元素，得到其它元素全为 0 的对角矩阵，例如：

$$\mathrm{diag}([3,2,1])=\left[\begin{array}{lll}3& 0& 0\\ 0& 2& 0\\ 0& 0& 1\end{array}\right]$$
因此
$$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}=\prod _{j=i}^{t-1}\mathrm{diag}\left({\sigma }^{\prime }\left({\mathbf{W}}_{xh}{\mathbf{x}}_{j+1}+{\mathbf{W}}_{hh}{\mathbf{h}}_j+\mathbf{b}\right)\right){\mathbf{W}}_{hh}$$
至此， $\frac{\partial \mathcal{L}}{\partial W_{hh}}$的梯度推导完成。

由于深度学习框架可以帮助我们自动推导梯度，只需要简单地了解循环神经网络的梯度传播方式即可。我们在推导$\frac{\partial \mathcal{L}}{\partial W_{hh}}$的过程中发现，$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}$的梯度包含了$W_{hh}$的连乘运算，我们会在后面介绍，这是导致循环神经网络训练困难的根本原因。

11.4 RNN 层使用方法

在介绍完循环神经网络的算法原理之后，我们来学习如何在 TensorFlow 中实现 RNN层。在 TensorFlow 中，可以通过 layers.SimpleRNNCell来完成$\sigma \left({\mathbf{W}}_{xh}{\mathbf{x}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1}+\mathbf{b}\right)$计算。需要注意的是，在 TensorFlow 中，RNN 表示通用意义上的循环神经网络，对于我们目前介绍的基础循环神经网络，它一般叫做 SimpleRNN。SimpleRNN 与 SimpleRNNCell 的区别在于，带 Cell 的层仅仅是完成了一个时间戳的前向运算，不带 Cell 的层一般是基于Cell 层实现的，它在内部已经完成了多个时间戳的循环运算，因此使用起来更为方便快捷。

我们先介绍 SimpleRNNCell 的使用方法，再介绍 SimpleRNN 层的使用方法。

11.4.1 SimpleRNNCell

以某输入特征长度 = 4，Cell 状态向量特征长度ℎ = 3为例，首先我们新建一个
SimpleRNNCell，不需要指定序列长度，代码如下：

cell=layers.SimpleRNNCell(3)#创建RNN Cell，内存向量长度为3
cell.build(input_shape=(None,4))#输出特征长度为n=4
print(cell.trainable_variables)#打印Wxh,Whh,b张量

[<tf.Variable 'kernel:0' shape=(4, 3) dtype=float32, numpy=
 array([[-0.19528645,  0.20379615, -0.04092252],
        [ 0.16957283,  0.5027101 ,  0.604565  ],
        [ 0.06750798, -0.69963527,  0.1719687 ],
        [-0.09530777, -0.14108837,  0.10946   ]], dtype=float32)>,
 <tf.Variable 'recurrent_kernel:0' shape=(3, 3) dtype=float32, numpy=
 array([[ 0.5461277 ,  0.68906   , -0.47638312],
        [-0.3704817 , -0.3113673 , -0.8750963 ],
        [ 0.75132406, -0.65440553, -0.08523771]], dtype=float32)>,
 <tf.Variable 'bias:0' shape=(3,) dtype=float32, numpy=array([0., 0., 0.], dtype=float32)>]

可以看到，SimpleRNNCell 内部维护了 3 个张量，kernel 变量即$W_{xh}$张量，recurrent_kernel
变量即$W_{hh}$张量，bias 变量即偏置向量。但是 RNN 的 Memory向量并不由SimpleRNNCell 维护，需要用户自行初始化向量$h_o$并记录每个时间戳上的$h_t$。

通过调用 Cell 实例即可完成前向运算：
$${\mathbf{o}}_t,\left[{\mathbf{h}}_t\right]=\mathrm{Cell}\left({\mathbf{x}}_t,\left[{\mathbf{h}}_{t-1}\right]\right)$$
对于 SimpleRNNCell 来说，$o_t=h_t$，并没有经过额外的线性层转换，是同一个对象；[$h_t$]通过一个 List 包裹起来，这么设置是为了与 LSTM、GRU 等 RNN 变种格式统一。在循环神经网络的初始化阶段，状态向量$h_0$一般初始化为全 0 向量，例如：

In [4]:
# 初始化状态向量，用列表包裹，统一格式
h0 = [tf.zeros([4, 64])]
x = tf.random.normal([4, 80, 100]) # 生成输入张量，4 个 80 单词的句子
xt = x[:,0,:] # 所有句子的第 1 个单词
# 构建输入特征 n=100,序列长度 s=80,状态长度=64 的 Cell
cell = layers.SimpleRNNCell(64)
out, h1 = cell(xt, h0) # 前向计算
print(out.shape, h1[0].shape)
Out[4]: (4, 64) (4, 64)

可以看到经过一个时间戳的计算后，输出和状态张量的 shape 都为[, ℎ]，打印出这两者的id 如下：

print(id(out), id(h1[0]))
Out[5]:2154936585256 2154936585256

两者 id 一致，即状态向量直接作为输出向量。对于长度为的训练来说，需要循环通过Cell 类次才算完成一次网络层的前向运算。例如：

h=h0#h保存每个时间戳上的状态向量列表
#在序列长度的维度解开输入，得到xt:[b,n]
for xt in tf.unstack(x,axis=1):
    out,h=cell(xt,h)#前向计算，out和h均被覆盖
out=out
# 最终输出可以聚合每个时间戳上的输出，也可以只取最后时间戳的输出

最后一个时间戳的输出变量 out 将作为网络的最终输出。实际上，也可以将每个时间戳上的输出保存，然后求和或者均值，将其作为网络的最终输出。

11.4.2 多层 SimpleRNNCell 网络

和卷积神经网络一样，循环神经网络虽然在时间轴上面展开了多次，但只能算一个网络层。通过在深度方向堆叠多个 Cell 类来实现深层卷积神经网络一样的效果，大大的提升网络的表达能力。但是和卷积神经网络动辄几十、上百的深度层数来比，循环神经网络很容易出现梯度弥散和梯度爆炸到现象，深层的循环神经网络训练起来非常困难，目前常见的循环神经网络模型层数一般控制在十层以内。

我们这里以两层的循环神经网络为例，介绍利用 Cell 方式构建多层 RNN 网络。首先新建两个SimpleRNNCell 单元，代码如下：

x=tf.random.normal([4,80,100])
xt=x[:,0,:]#取第一个时间戳的输入x0
# 构建2个Cell，先cell0，后cell1，内存状态向量长度都为64
cell0=layers.SimpleRNNCell(64)
cell1=layers.SimpleRNNCell(64)
h0=[tf.zeros([4,64])]#cell0的初始状态向量
h1=[tf.zeros([4,64])]#cell1的初始状态向量

在时间轴上面循环计算多次来实现整个网络的前向运算，每个时间戳上的输入 xt 首先通过第一层，得到输出 out0，再通过第二层，得到输出 out1，代码如下：

for xt in tf.unstack(x,axis=1):
    # xt作为输入，输出为out0
    out0,h0=cell0(xt,h0)
    # 上一个cell的输出out0作为本cell的输入
    out1,h1=cell1(out0,h1)

上述方式先完成一个时间戳上的输入在所有层上的传播，再循环计算完所有时间戳上的输入。

实际上，也可以先完成输入在第一层上所有时间戳的计算，并保存第一层在所有时间戳上的输出列表，再计算第二层、第三层等的传播。代码如下：

# 保存上一层的所有时间戳上面的输出
#保存上一层的所有时间戳的输出
niddle_sequences=[]
#计算第一层的所有时间戳上的输出，并保存
for xt in tf.unstack(x,axis=1):
    out0,h0=cell0(xt,h0)
    niddle_sequences.append(out0)
#计算第二层的所有时间戳的输出
#如果不是末层，需要保存所有时间戳上面的输出
for xt in niddle_sequences:
    out1,h1=cell1(xt,h1)

使用这种方式的话，我们需要一个额外的 List 来保存上一层所有时间戳上面的状态信息：middle_sequences.append(out0)。这两种方式效果相同，可以根据个人喜好选择编程风格。

需要注意的是，循环神经网络的每一层、每一个时间戳上面均有状态输出，那么对于后续任务来说，我们应该收集哪些状态输出最有效呢？一般来说，最末层 Cell 的状态有可能保存了高层的全局语义特征，因此一般使用最末层的输出作为后续任务网络的输入。更特别地，每层最后一个时间戳上的状态输出包含了整个序列的全局信息，如果只希望选用一个状态变量来完成后续任务，比如情感分类问题，一般选用最末层、最末时间戳的状态输出最为合适。

11.4.3 SimpleRNN 层

通过 SimpleRNNCell层的使用，我们可以非常深入地理解循环神经网络前向运算的每个细节，但是在实际使用中，为了简便，不希望手动参与循环神经网络内部的计算过程，比如每一层的状态向量的初始化，以及每一层在时间轴上展开的运算。通过 SimpleRNN层高层接口可以非常方便地帮助我们实现此目的。

比如我们要完成单层循环神经网络的前向运算，可以方便地实现如下：

layer=layers.SimpleRNN(64)#创建状态向量长度为64的SimpleRNN层
x=tf.random.normal([4,80,100])
out=layer(x)#和普通卷积网络一样，一行代码即可获得输出
print(out)

TensorShape([4, 64])

可以看到，通过 SimpleRNN 可以仅需一行代码即可完成整个前向运算过程，它默认返回最后一个时间戳上的输出。

如果希望返回所有时间戳上的输出列表，可以设置 return_sequences=True 参数，代码如下：

#设置RNN层，设置返回所有时间戳上的输出
layer=layers.SimpleRNN(64,return_sequences=True)#创建状态向量长度为64的SimpleRNN层
x=tf.random.normal([4,80,100])
out=layer(x)#前向计算
print(out)#输出，自动进行了concat操作

<tf.Tensor: id=12654, shape=(4, 80, 64), dtype=float32, numpy=
array([[[ 0.31804922, 0.7904409 , 0.13204293, ..., 0.02601025,
 -0.7833339 , 0.65577114],…>

可以看到，返回的输出张量 shape 为[4,80,64]，中间维度的 80 即为时间戳维度。同样的，对于多层循环神经网络，我们可以通过堆叠多个 SimpleRNN 实现，如两层的网络，用法和普通的网络类似。例如：

x=tf.random.normal([4,80,100])
net=keras.Sequential([#构建2层RNN网络
    #最末层外，都需要返回所有时间戳的输出，用作下一层的输入
    layers.SimpleRNN(64,return_sequences=True),
    layers.SimpleRNN(64),
])
out=net(x)#前向计算

每层都需要上一层在每个时间戳上面的状态输出，因此除了最末层以外，所有的 RNN 层都需要返回每个时间戳上面的状态输出，通过设置return_sequences=True 来实现。可以看到，使用 SimpleRNN 层，与卷积神经网络的用法类似，非常简洁和高效.

11.5 RNN 情感分类问题实战

现在利用基础的 RNN 网络来挑战情感分类问题。网络结构如图 11.9 所示，RNN 网络共两层，循环提取序列信号的语义特征，利用第 2 层 RNN 层的最后时间戳的状态向量$h_s^{(2)}$作为句子的全局语义特征表示，送入全连接层构成的分类网络 3，得到样本为积极情感的概率P(为积极情感|) ∈ [0,1]。

11.5.1 数据集

这里使用经典的 IMDB 影评数据集来完成情感分类任务。IMDB 影评数据集包含了50000 条用户评价，评价的标签分为消极和积极，其中 IMDB 评级<5 的用户评价标注为0，即消极；IMDB 评价>=7 的用户评价标注为 1，即积极。25000 条影评用于训练集，25,000 条用于测试集。

通过 Keras 提供的数据集 datasets 工具即可加载 IMDB 数据集，代码如下：

from tensorflow import keras

batchsz=128#批量大小
total_words=10000 #词汇表大小N_vocab
max_review_len=80 #句子最大长度s，大于的句子部分将阶段，小于的将填充
embedding_len=100 #词向量特征长度n
# 加载IMDB数据集，此处的数据采用数字编码，一个数字代表一个单词
(x_train,y_train),(x_test,y_test)=keras.datasets.imdb.load_data(num_words=total_words)
#打印输入的形状，标签的形状
print(x_train.shape,len(x_train[0]),y_train.shape)
print(x_test.shape,len(x_test[0]),y_test.shape)

(25000,) 218 (25000,)
(25000,) 68 (25000,)

可以看到，x_train 和 x_test 是长度为 25,000 的一维数组，数组的每个元素是不定长 List，保存了数字编码的每个句子，例如训练集的第一个句子共有 218 个单词，测试集的第一个句子共有 68 个单词，每个句子都包含了句子起始标志 ID。

那么每个单词是如何编码为数字的呢？我们可以通过查看它的编码表获得编码方案，例如：

#数字编码
word_index=keras.datasets.imdb.get_word_index()
#打印出编码表的单词和对应的句子
for k,v in word_index.items():
  print(k,v)
  
…diamiter 88301
moveis 88302
mardi 14352
wells' 11583
850pm 88303…

由于编码表的键为单词，值为 ID，这里翻转编码表，并添加标志位的编码 ID，代码如下：

word_index={k:(v+3) for k,v in word_index.items()}
word_index['']=0 #填充标志
word_index['']=1 #起始标志
word_index['']=2 #未知单词的标志
word_index['UNUSED']=3

#翻转编码表
reverse_word_index=dict([(value,key) for(key,value)in word_index.items()])

对于一个数字编码的句子，通过如下函数转换为字符串数据：

def decode_review(text):
  return ' '.join(reverse_word_index.get(i,'?') for i in text])

例如转换某个句子，代码如下：

decode_review(x_train[0])

"<START> this film was just brilliant casting location scenery story
direction everyone's…<UNK> father came from…

对于长度参差不齐的句子，人为设置一个阈值，对大于此长度的句子，选择截断部分单词，可以选择截去句首单词，也可以截去句末单词；对于小于此长度的句子，可以选择在句首或句尾填充，句子截断功能可以通过 keras.preprocessing.sequence.pad_sequences()函数方便实现，例如：

# 截断和填充句子，使得等长，此处长句子保留句子后面的部分，短句子在前面填充
x_train=keras.preprocessing.sequence.pad_sequences(x_train,maxlen=max_review_len)
x_test=keras.preprocessing.sequence.pad_sequences(x_test,maxlen=max_review_len)

截断或填充为相同长度后，通过 Dataset 类包裹成数据集对象，并添加常用的数据集处理流程，代码如下：

import tensorflow as tf
#构建数据集，打散，批量，并丢掉最后一个不够batchsz的batch
db_train=tf.data.Dataset.from_tensor_slices((x_train,y_train))
db_train=db_train.shuffle(1000).batch(batchsz,drop_remainder=True)
db_test=tf.data.Dataset.from_tensor_slices((x_test,y_test))
db_test=db_test.batch(batchsz,drop_remainder=True)
#统计数据集属性
print("x_train shape",x_train.shape,tf.reduce_max(y_train),tf.reduce_min(y_train))
print('x_test shape',x_test.shape)

x_train shape: (25000, 80) tf.Tensor(1, shape=(), dtype=int64) tf.Tensor(0,
shape=(), dtype=int64)
x_test shape: (25000, 80)

可以看到截断填充后的句子长度统一为 80，即设定的句子长度阈值。drop_remainder=True参数设置丢弃掉最后一个 Batch，因为其真实的 Batch Size 可能小于预设的 Batch Size。

11.5.2 网络模型

我们创建自定义的模型类 MyRNN，继承自 Model 基类，需要新建 Embedding 层，两个 RNN 层，分类网络层，代码如下：

class MyRNN(keras.Model):
    # Cell方式构建多层网络
    def __init__(self,units):
        #[b,64],构建cell初始化状态向量，重复使用
        self.state0=[tf.zeros([batchsz,units])]
        self.state1=[tf.zeros([batchsz,units])]
        # 词向量编码 [b,80]=>[b,80,100]
        self.embedding=layers.Embedding(total_words,embedding_len,input_length=max_review_len)
        #构建两个Cell，使用dropout技术防止过拟合
        self.rnn_cell0=layers.SimpleRNNCell(units,dropout=0.5)
        self.run_cell1=layers.SimpleRNNCell(units,dropout=0.5)
        #构建分类网络，用于将CELL的输出特征进行分类，二分类
        #[b,80,100]=>[b,64]=>[b,1]
        self.outlayer=layers.Dense(1)

其中词向量编码为长度 = 100，RNN 的状态向量长度ℎ = units参数，分类网络完成 2 分类任务，故输出节点设置为 1。

前向传播逻辑如下：输入序列通过 Embedding 层完成词向量编码，循环通过两个 RNN层，提取语义特征，取最后一层的最后时间戳的状态向量输出送入分类网络，经过Sigmoid 激活函数后得到输出概率。代码如下：

     def call(self,inputs,training=None):
        x=inputs #[b,80]
        #获取词向量，[b,80]=>[b,80,100]
        x=self.embedding()
        #通过两个RNN CELL,[b,80,100]>[b,64]
        state0=self.state0
        state1=self.state1
        for word in tf.unstack(x,axis=1):# word:[b,100]
            out0,state0=self.rnn_cell0(word,state0,training)
            out1,state1=self.rnn_cell1(out0,state1,training)
            
        # 末层最后一个输出作为分类网络的输入:[b,64]=>[b,1]
        x=self.outlayer(out1,training)
        # 通过激活函数，p(y is pos|x)
        prob=tf.sigmoid(x)
        
        return prob

11.5.3 训练与测试

为了简便，这里使用 Keras 的 Compile&Fit 方式训练网络，设置优化器为 Adam 优化器，学习率为 0.001，误差函数选用 2 分类的交叉熵损失函数 BinaryCrossentropy，测试指标采用准确率即可。代码如下：

def main():
    units=64 #RNN状态向量长度n
    epochs=20 #训练epochs
    
    model=MyRNN(units)#创建模板
    #装配
    model.compile(optimizer=optimizers.Adam(0.001),loss=losses.BinaryCrossentropy(),metrics=['accuracy'])
    #训练和验证
    model.fit(db_train,epochs=epochs,validation_data=db_test)
    #测试
    model.evaluate(db_test)

网络固定训练 20 个 Epoch 后，在测试集上获得了 80.1%的准确率。

我们整理一下代码：

#!/usr/bin/env python
# encoding: utf-8
import os
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers, losses, optimizers, Sequential

tf.random.set_seed(22)
np.random.seed(22)
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'


def load_dataset(batchsz, total_words, max_review_len):
    # 加载IMDB数据集，此处的数据采用数字编码，一个数字代表一个单词
    (x_train, y_train), (x_test, y_test) = keras.datasets.imdb.load_data(num_words=total_words)
    print(x_train.shape, len(x_train[0]), y_train.shape)
    print(x_test.shape, len(x_test[0]), y_test.shape)

    # x_train:[b, 80]
    # x_test: [b, 80]
    # 截断和填充句子，使得等长，此处长句子保留句子后面的部分，短句子在前面填充
    x_train = keras.preprocessing.sequence.pad_sequences(x_train, maxlen=max_review_len)
    x_test = keras.preprocessing.sequence.pad_sequences(x_test, maxlen=max_review_len)
    # 构建数据集，打散，批量，并丢掉最后一个不够batchsz的batch
    db_train = tf.data.Dataset.from_tensor_slices((x_train, y_train))
    db_train = db_train.shuffle(1000).batch(batchsz, drop_remainder=True)
    db_test = tf.data.Dataset.from_tensor_slices((x_test, y_test))
    db_test = db_test.batch(batchsz, drop_remainder=True)
    print('x_train shape:', x_train.shape, tf.reduce_max(y_train), tf.reduce_min(y_train))
    print('x_test shape:', x_test.shape)
    return db_train, db_test


class MyRNN(keras.Model):
    # Cell方式构建多层网络
    def __init__(self, units, batchsz, total_words, embedding_len, max_review_len):
        super(MyRNN, self).__init__()
        # [b, 64]，构建Cell初始化状态向量，重复使用
        self.state0 = [tf.zeros([batchsz, units])]
        self.state1 = [tf.zeros([batchsz, units])]
        # 词向量编码 [b, 80] => [b, 80, 100]
        self.embedding = layers.Embedding(total_words, embedding_len,
                                          input_length=max_review_len)
        # 构建2个Cell
        self.rnn_cell0 = layers.SimpleRNNCell(units, dropout=0.5)
        self.rnn_cell1 = layers.SimpleRNNCell(units, dropout=0.5)
        # 构建分类网络，用于将CELL的输出特征进行分类，2分类
        # [b, 80, 100] => [b, 64] => [b, 1]
        self.outlayer = Sequential([
            layers.Dense(units),
            layers.Dropout(rate=0.5),
            layers.ReLU(),
            layers.Dense(1)])

    def call(self, inputs, training=None):
        x = inputs  # [b, 80]
        # embedding: [b, 80] => [b, 80, 100]
        x = self.embedding(x)
        # rnn cell compute,[b, 80, 100] => [b, 64]
        state0 = self.state0
        state1 = self.state1
        for word in tf.unstack(x, axis=1):  # word: [b, 100]
            out0, state0 = self.rnn_cell0(word, state0, training)
            out1, state1 = self.rnn_cell1(out0, state1, training)
        # 末层最后一个输出作为分类网络的输入: [b, 64] => [b, 1]
        x = self.outlayer(out1, training)
        # p(y is pos|x)
        prob = tf.sigmoid(x)

        return prob


def main():
    batchsz = 128  # 批量大小
    total_words = 10000  # 词汇表大小N_vocab
    embedding_len = 100  # 词向量特征长度f
    max_review_len = 80  # 句子最大长度s，大于的句子部分将截断，小于的将填充

    db_train, db_test = load_dataset(batchsz, total_words, max_review_len)

    units = 64  # RNN状态向量长度f
    epochs = 20  # 训练epochs

    model = MyRNN(units, batchsz, total_words, embedding_len, max_review_len)
    # 装配
    model.compile(optimizer=optimizers.RMSprop(0.001),
                  loss=losses.BinaryCrossentropy(),
                  metrics=['accuracy'],
                  experimental_run_tf_function=False)
    # 训练和验证
    model.fit(db_train, epochs=epochs, validation_data=db_test)
    # 测试
    model.evaluate(db_test)


if __name__ == '__main__':
    main()

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/imdb.npz
17465344/17464789 [==============================] - 1s 0us/step
(25000,) 218 (25000,)
(25000,) 68 (25000,)
x_train shape: (25000, 80) tf.Tensor(1, shape=(), dtype=int64) tf.Tensor(0, shape=(), dtype=int64)
x_test shape: (25000, 80)
Epoch 1/20
195/195 [==============================] - 8s 39ms/step - loss: 0.6995 - accuracy: 0.5142 - val_loss: 0.6713 - val_accuracy: 0.6322
Epoch 2/20
195/195 [==============================] - 6s 33ms/step - loss: 0.5651 - accuracy: 0.7033 - val_loss: 0.4446 - val_accuracy: 0.8012
Epoch 3/20
195/195 [==============================] - 7s 34ms/step - loss: 0.4138 - accuracy: 0.8274 - val_loss: 0.4405 - val_accuracy: 0.8195
Epoch 4/20
195/195 [==============================] - 7s 34ms/step - loss: 0.3680 - accuracy: 0.8508 - val_loss: 0.3827 - val_accuracy: 0.8368
Epoch 5/20
195/195 [==============================] - 7s 34ms/step - loss: 0.3278 - accuracy: 0.8698 - val_loss: 0.3868 - val_accuracy: 0.8333
Epoch 6/20
195/195 [==============================] - 6s 33ms/step - loss: 0.2972 - accuracy: 0.8877 - val_loss: 0.4172 - val_accuracy: 0.8357
Epoch 7/20
195/195 [==============================] - 6s 33ms/step - loss: 0.2577 - accuracy: 0.9025 - val_loss: 0.4797 - val_accuracy: 0.8204
Epoch 8/20
195/195 [==============================] - 6s 33ms/step - loss: 0.2207 - accuracy: 0.9172 - val_loss: 0.5070 - val_accuracy: 0.8215
Epoch 9/20
195/195 [==============================] - 7s 34ms/step - loss: 0.1812 - accuracy: 0.9335 - val_loss: 0.5768 - val_accuracy: 0.7917
Epoch 10/20
195/195 [==============================] - 6s 32ms/step - loss: 0.1480 - accuracy: 0.9460 - val_loss: 0.6151 - val_accuracy: 0.8134
Epoch 11/20
195/195 [==============================] - 6s 33ms/step - loss: 0.1294 - accuracy: 0.9526 - val_loss: 0.6338 - val_accuracy: 0.8044
Epoch 12/20
195/195 [==============================] - 6s 33ms/step - loss: 0.1150 - accuracy: 0.9580 - val_loss: 0.6984 - val_accuracy: 0.8154
Epoch 13/20
195/195 [==============================] - 7s 34ms/step - loss: 0.0939 - accuracy: 0.9655 - val_loss: 0.7321 - val_accuracy: 0.8102
Epoch 14/20
195/195 [==============================] - 7s 35ms/step - loss: 0.0786 - accuracy: 0.9719 - val_loss: 0.9008 - val_accuracy: 0.8123
Epoch 15/20
195/195 [==============================] - 6s 33ms/step - loss: 0.0761 - accuracy: 0.9728 - val_loss: 0.7766 - val_accuracy: 0.8022
Epoch 16/20
195/195 [==============================] - 6s 33ms/step - loss: 0.0634 - accuracy: 0.9781 - val_loss: 0.9109 - val_accuracy: 0.7759
Epoch 17/20
195/195 [==============================] - 6s 33ms/step - loss: 0.0560 - accuracy: 0.9804 - val_loss: 0.9310 - val_accuracy: 0.7843
Epoch 18/20
195/195 [==============================] - 6s 32ms/step - loss: 0.0537 - accuracy: 0.9809 - val_loss: 0.9188 - val_accuracy: 0.7863
Epoch 19/20
195/195 [==============================] - 6s 33ms/step - loss: 0.0496 - accuracy: 0.9836 - val_loss: 1.0805 - val_accuracy: 0.8076
Epoch 20/20
195/195 [==============================] - 6s 33ms/step - loss: 0.0441 - accuracy: 0.9851 - val_loss: 0.9864 - val_accuracy: 0.8066
195/195 [==============================] - 2s 9ms/step - loss: 0.9864 - accuracy: 0.8066

11.6 梯度弥散和梯度爆炸

循环神经网络的训练并不稳定，网络的深度也不能任意的加深。那么，为什么循环神经网络会出现训练困难的问题呢？简单回顾梯度推导中的关键表达式：
$$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}=\prod _{j=i}^{t-1}\mathrm{diag}\left({\sigma }^{\prime }\left({\mathbf{W}}_{xh}{\mathbf{x}}_{j+1}+{\mathbf{W}}_{hh}{\mathbf{h}}_j+\mathbf{b}\right)\right){\mathbf{W}}_{hh}$$
也就是说，从时间戳到时间戳的梯度$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}$包含了$W_{hh}$的连乘运算。当$W_{hh}$的最大特征值(Largest Eignvalue)小于 1 时，多次连乘运算会使得$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}$的元素值接近于零；当$W_{hh}$的值大于 1时，多次连乘运算会使得$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_i}$的元素值爆炸式增长。

我们可以从下面的两个例子直观地感受一下梯度弥散和梯度爆炸现象的产生，代码如下：

import tensorflow as tf
w=tf.ones([2,2])
eigenvalues=tf.linalg.eigh(w)[0]#计算矩阵的特征值
print(eigenvalues)

<tf.Tensor: id=923, shape=(2,), dtype=float32, numpy=array([0., 2.],
dtype=float32)>

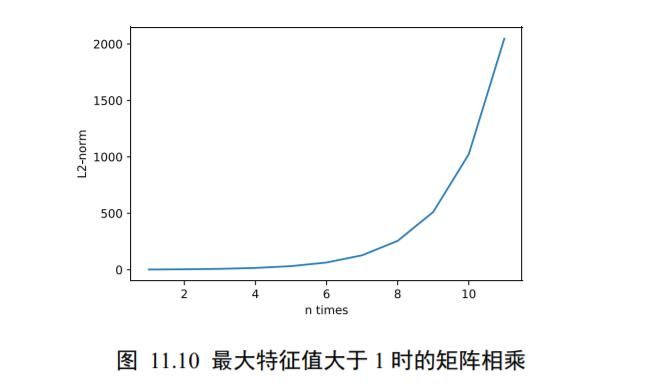
可以看到，全 1 矩阵的最大特征值为 2。计算矩阵的$W_1$~$W_{10}$ 运算结果，并绘制为次方与矩阵的 L2-范数的曲线图，如图 11.10 所示。可以看到，当矩阵的最大特征值大于 1时，矩阵多次相乘会使得结果越来越大。

import matplotlib.pyplot as plt
val=[w]
for i in range(10):
    val.append([val[-1]@w])
norm=list(map(lambda x:tf.norm(x).numpy(),val))
plt.plot(range(1,12),norm)
plt.show()


[2.0, 4.0, 8.0, 16.0, 32.0, 64.0, 128.0, 256.0, 512.0, 1024.0, 2048.0]

考虑最大特征值小于 1 时的情况。例如：

W = tf.ones([2,2])*0.4 # 任意创建某矩阵
eigenvalues = tf.linalg.eigh(W)[0] # 计算特征值
print(eigenvalues)

tf.Tensor([0. 0.8], shape=(2,), dtype=float32)

可以看到此时的矩阵最大特征值是 0.8。相同的方法，考虑矩阵的多次相乘运算结果，代码如下：

import matplotlib.pyplot as plt
val=[w]
for i in range(10):
    val.append([val[-1]@w])
norm=list(map(lambda x:tf.norm(x).numpy(),val))
plt.plot(range(1,12),norm)
plt.show()

它的 L2-范数曲线如图 11.11 所示。可以看到，当矩阵的最大特征值小于 1 时，矩阵多次相乘会使得结果越来越小，接近于 0。

我们把梯度值接近于 0 的现象叫做梯度弥散(Gradient Vanishing)，把梯度值远大于 1 的现象叫做梯度爆炸(Gradient Exploding)。梯度弥散和梯度爆炸是神经网络优化过程中间比较容易出现的两种情况，也是不利于网络训练的。那么梯度弥散和梯度爆炸具体表现在哪些地方呢？

考虑梯度下降算法：
$${\theta }^{\prime }=\theta -\eta {\nabla }_{\theta }\mathcal{L}$$
当出现梯度弥散时， ∇ℒ ≈ 0，此时′ ≈ ，也就是说每次梯度更新后参数基本保持不变，神经网络的参数长时间得不到更新，具体表现为ℒ几乎保持不变，其它评测指标，如准确度，也保持不变。
当出现梯度爆炸时，∇ℒ ≫ 1，此时梯度的更新步长η∇ℒ非常大，使得更新后的′与差距很大，网络ℒ出现突变现象，甚至可能出现来回震荡、不收敛的现象。

通过推导循环神经网络的梯度传播公式，我们发现循环神经网络很容易出现梯度弥散和梯度爆炸的现象。那么怎么解决这两个问题呢？

11.6.1 梯度裁剪

梯度爆炸可以通过梯度裁剪(Gradient Clipping)的方式在一定程度上的解决。梯度裁剪与张量限幅非常类似，也是通过将梯度张量的数值或者范数限制在某个较小的区间内，从而将远大于 1 的梯度值减少，避免出现梯度爆炸。

在深度学习中，有 3 种常用的梯度裁剪方式。

❑ 直接对张量的数值进行限幅，使得张量的所有元素$w_{i,j}$∈ [min,max]。在 TensorFlow中，可以通过 tf.clip_by_value()函数来实现。例如:

a=tf.random.uniform([2,2])
print(tf.clip_by_value(a,0.4,0.6))

<tf.Tensor: id=1262, shape=(2, 2), dtype=float32, numpy=
array([[0.5410726, 0.6 ],
         [0.4 , 0.6 ]], dtype=float32)>

❑ 通过限制梯度张量的范数来实现梯度裁剪。比如对的二范数$||w|{|}_2$约束在[0, max]之间，如果$||w|{|}_2$大于max值，则按照
$$W^{\prime }=\frac{W}{\Vert W{\Vert }_2}\cdot \max$$
方式将$||w^{\prime }|{|}_2$约束max内。可以通过 tf.clip_by_norm 函数方便的实现梯度张量裁剪。例如：

a=tf.random.uniform([2,2])*5
# 按范数方式裁剪
b=tf.clip_by_norm(a,5)
# 裁剪前和裁剪后的张量范数
print(tf.norm(a),tf.norm(b))

(<tf.Tensor: id=1338, shape=(), dtype=float32, numpy=5.380655>,
<tf.Tensor: id=1343, shape=(), dtype=float32, numpy=5.0>)

可以看到，对于大于max的 L2 范数的张量，通过裁剪后范数值缩减为 5。

❑ 神经网络的更新方向是由所有参数的梯度张量共同表示的，前两种方式只考虑单个梯度张量的限幅，会出现网络更新方向发生变动的情况。如果能够考虑所有参数的梯度的范数，实现等比例的缩放，那么就能既很好地限制网络的梯度值，同时不改变网络的更新方向。这就是第三种梯度裁剪的方式：全局范数裁剪。在 TensorFlow 中，可以通过 tf.clip_by_global_norm 函数快捷地缩放整体网络梯度的范数。

令()表示网络参数的第个梯度张量，首先通过

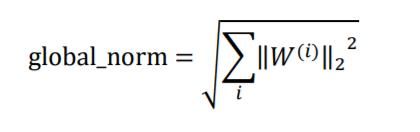
计算网络的总范数global_norm，对第个参数()，通过

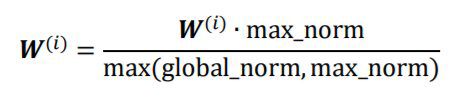
进行裁剪，其中max_norm是用户指定的全局最大范数值。例如：

w1=tf.random.normal([3,3])#创建梯度张量1
w2=tf.random.normal([3,3])#创建梯度张量2
# 计算global norm
global_norm=tf.math.sqrt(tf.norm(w1)**2+tf.norm(w2)**2)
# 根据global_norm和max_norm=2裁剪
(ww1,ww2),global_norm=tf.clip_by_global_norm([w1,w2],2)
# 计算裁剪后的张量组的global norm
global_norm2=tf.math.sqrt(tf.norm(ww1)**2+tf.norm(ww2)**2)
#打印裁剪前的全局范数和裁剪后的全局范数
print(global_norm,global_norm2)

tf.Tensor(4.1547523, shape=(), dtype=float32)
tf.Tensor(2.0, shape=(), dtype=float32)

可以看到，通过裁剪后，网络参数的梯度组的总范数缩减到max_norm = 2。需要注意的是，tf.clip_by_global_norm 返回裁剪后的张量 List 和 global_norm 这两个对象，其中global_norm 表示裁剪前的梯度总范数和。

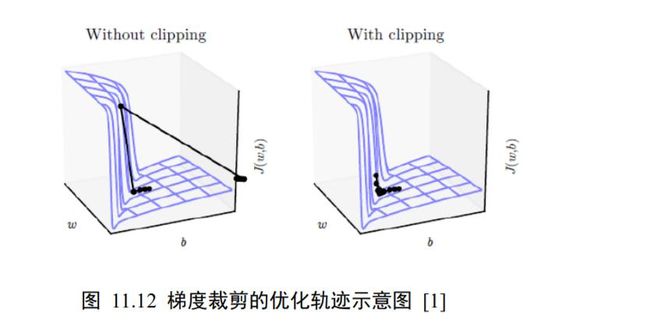
通过梯度裁剪，可以较大程度的抑制梯度爆炸现象。如下图 11.12 所示，图中曲面表示的(, )函数在不同网络参数和下的误差值，其中有一块区域(, )函数的梯度变化较大，一旦网络参数进入此区域，很容易出现梯度爆炸的现象，使得网络状态迅速恶化。
图 11.12 右演示了添加梯度裁剪后的优化轨迹，由于对梯度进行了有效限制，使得每次更新的步长得到有效控制，从而防止网络突然恶化。

在网络训练时，梯度裁剪一般在计算出梯度后，梯度更新之前进行。例如：

with tf.GradientTape() as tape:
    logits=model(x)#前向传播
    loss=criteon(y,logits)#误差计算
#计算梯度值
grads=tape.gradient(loss,model.trainable_variables)
grads,_=tf.clip_by_global_norm(grads,25)#全局梯度裁剪
#利用裁剪后的梯度张量更新参数
optimizer.apply_gradients(zip(grads,model.trainable_variables))

11.6.2 梯度弥散

对于梯度弥散现象，可以通过增大学习率、减少网络深度、添加 Skip Connection 等一系列的措施抑制。

增大学习率可以在一定程度防止梯度弥散现象，当出现梯度弥散时，网络的梯度∇ℒ接近于 0，此时若学习率也较小，如η = 1e − 5，则梯度更新步长更加微小。通过增大学习率，如令 = 1e − 2，有可能使得网络的状态得到快速更新，从而逃离梯度弥散区域。

对于深层次的神经网络，梯度由最末层逐渐向首层传播，梯度弥散一般更有可能出现在网络的开始数层。在深度残差网络出现之前，几十上百层的深层网络训练起来非常困难，前面数层的网络梯度极容易出现梯度离散现象，从而使得网络参数长时间得不到更新。深度残差网络较好地克服了梯度弥散现象，从而让神经网络层数达到成百上千。一般来说，减少网络深度可以减轻梯度弥散现象，但是网络层数减少后，网络表达能力也会偏弱，需要用户自行平衡。

11.7 RNN 短时记忆

循环神经网络除了训练困难，还有一个更严重的问题，那就是短时记忆(Short-term memory)。考虑一个长句子：

今天天气太美好了，尽管路上发生了一件不愉快的事情，…，我马上调整好状态，开 开心心地准备迎接美好的一天。

根据我们的理解，之所以能够“开开心心地准备迎接美好的一天”，在于句子最开始处点名了“今天天气太美好了”。可见人类是能够很好地理解长句子的，但是循环神经网络却不一定。研究人员发现，循环神经网络在处理较长的句子时，往往只能够理解有限长度内的信息，而对于位于较长范围类的有用信息往往不能够很好的利用起来。我们把这种现象叫做短时记忆。

那么，能不能够延长这种短时记忆，使得循环神经网络可以有效利用较大范围内的训练数据，从而提升性能呢？1997 年，瑞士人工智能科学家 Jürgen Schmidhuber 提出了长短时记忆网络(Long Short-Term Memory，简称 LSTM)。LSTM 相对于基础的 RNN 网络来说，记忆能力更强，更擅长处理较长的序列信号数据，LSTM 提出后，被广泛应用在序列预测、自然语言处理等任务中，几乎取代了基础的 RNN 模型。

接下来，我们将介绍更加流行、更强大的 LSTM 网络。

11.8 LSTM 原理

基础的 RNN 网络结构如图 11.13 所示，上一个时间戳的状态向量$h_{t-1}$与当前时间戳的输入$x_t$经过线性变换后，通过激活函数ℎ后得到新的状态向量$h_t$。
相对于基础的 RNN网络只有一个状态向量$h_t$，LSTM 新增了一个状态向量$c_t$，同时引入了门控(Gate)机制，通过门控单元来控制信息的遗忘和刷新，如图 11.14 所示。

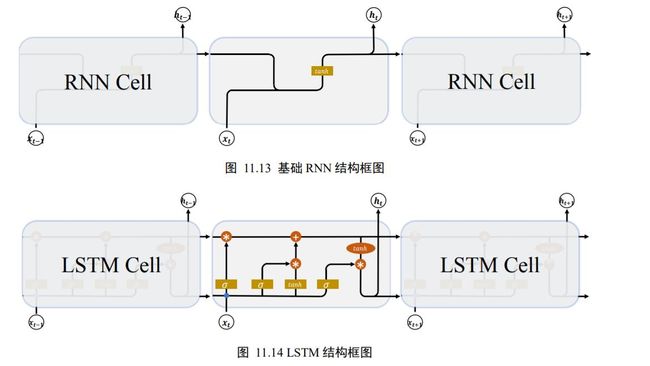
在 LSTM 中，有两个状态向量和$h$ ，其中作为 LSTM 的内部状态向量，可以理解为LSTM 的内存状态向量 Memory，而 $h$表示 LSTM 的输出向量。相对于基础的 RNN 来说，LSTM 把内部 Memory 和输出分开为两个变量，同时利用三个门控：输入门(Input Gate)、遗忘门(Forget Gate)和输出门(Output Gate)来控制内部信息的流动。

门控机制可以理解为控制数据流通量的一种手段，类比于水阀门：当水阀门全部打开时，水流畅通无阻地通过；当水阀门全部关闭时，水流完全被隔断。
在 LSTM 中，阀门开和程度利用门控值向量表示，如图 11.15 所示，通过()激活函数将门控制压缩到[0,1]之间区间，当() = 0时，门控全部关闭，输出 = 0；当() = 1时，门控全部打开，输出 = 。通过门控机制可以较好地控制数据的流量程度。

下面我们分别来介绍三个门控的原理及其作用。

11.8.1 遗忘门

遗忘门作用于 LSTM 状态向量上面，用于控制上一个时间戳的记忆$c_{t-1}$对当前时间戳的影响。遗忘门的控制变量${\mathbf{g}}_f$由
$${\mathbf{g}}_f=\sigma \left({\mathbf{W}}_f\left[{\mathbf{h}}_{t-1},{\mathbf{x}}_t\right]+{\mathbf{b}}_f\right)$$

产生，如图 11.16 所示，其中和为遗忘门的参数张量，可由反向传播算法自动优化，为激活函数，一般使用 Sigmoid 函数。当门控${\mathbf{g}}_f$ = 1时，遗忘门全部打开，LSTM 接受上一个状态$c_{t-1}$的所有信息；当门控${\mathbf{g}}_f$ = 0时，遗忘门关闭，LSTM 直接忽略$c_{t-1}$，输出为 0的向量。这也是遗忘门的名字由来。

经过遗忘门后，LSTM 的状态向量变为${\mathbf{g}}_f$$c_{t-1}$。

11.8.2 输入门

输入门用于控制 LSTM 对输入的接收程度。首先通过对当前时间戳的输入$x_t$和上一个时间戳的输出$h_{t-1}$做非线性变换得到新的输入向量${\tilde{\mathbf{c}}}_t$
$${\tilde{\mathbf{c}}}_t=\tanh \left({\mathbf{W}}_c\left[{\mathbf{h}}_{t-1},{\mathbf{x}}_t\right]+{\mathbf{b}}_c\right)$$

其中$w_c$和$b_c$为输入门的参数，需要通过反向传播算法自动优化，tanh 为激活函数，用于将输入标准化到[−1,1]区间。${\tilde{\mathbf{c}}}_t$并不会全部刷新进入 LSTM 的 Memory，而是通过输入门控制接受输入的量。输入门的控制变量同样来自于输入$x_t$和输出 $h_{t-1}$：
$${\mathbf{g}}_i=\sigma \left({\mathbf{W}}_i\left[{\mathbf{h}}_{t-1},{\mathbf{x}}_t\right]+{\mathbf{b}}_i\right)$$

其中$w_i$和$b_i$为输入门的参数，需要通过反向传播算法自动优化，为激活函数，一般使用Sigmoid 函数。输入门控制变量${\mathbf{g}}_i$决定了 LSTM 对当前时间戳的新输入${\tilde{\mathbf{c}}}_t$的接受程度：当${\mathbf{g}}_i$= 0时，LSTM 不接受任何的新输入${\tilde{\mathbf{c}}}_t$；当${\mathbf{g}}_i$= 1时，LSTM 全部接受新输入${\tilde{\mathbf{c}}}_t$，如图11.17 所示。

经过输入门后，待写入 Memory 的向量为${\mathbf{g}}_i$${\tilde{\mathbf{c}}}_t$。

11.8.3 刷新 Memory

在遗忘门和输入门的控制下，LSTM 有选择地读取了上一个时间戳的记忆$c_{t-1}$和当前时间戳的新输入${\tilde{\mathbf{c}}}_t$，状态向量${\mathbf{c}}_t$的刷新方式为：
$${\mathbf{c}}_t={\mathbf{g}}_i{\tilde{\mathbf{c}}}_t+{\mathbf{g}}_f{\mathbf{c}}_{t-1}$$

得到的新状态向量${\mathbf{c}}_t$即为当前时间戳的状态向量，如图 11.17 所示。

11.8.4 输出门

LSTM 的内部状态向量${\mathbf{c}}_t$并不会直接用于输出，这一点和基础的 RNN 不一样。基础的RNN 网络的状态向量$h$ 既用于记忆，又用于输出，所以基础的 RNN 可以理解为状态向量和输出向量$h$是同一个对象。在 LSTM 内部，状态向量并不会全部输出，而是在输出门的作用下有选择地输出。输出门的门控变量${\mathbf{g}}_o$为：
$${\mathbf{g}}_o=\sigma \left({\mathbf{W}}_o\left[{\mathbf{h}}_{t-1},{\mathbf{x}}_t\right]+{\mathbf{b}}_o\right)$$

其中$w_o$和$b_o$为输出门的参数，同样需要通过反向传播算法自动优化，为激活函数，一般使用 Sigmoid 函数。当输出门${\mathbf{g}}_o$= 0时，输出关闭，LSTM 的内部记忆完全被隔断，无法用作输出，此时输出为 0 的向量；当输出门${\mathbf{g}}_o$ = 1时，输出完全打开，LSTM 的状态向量$c_t$全部用于输出。LSTM 的输出由：
$${\mathbf{h}}_t={\mathbf{g}}_o\cdot \tanh \left({\mathbf{c}}_t\right)$$

产生，即内存向量$c_t$经过tanh激活函数后与输出门作用，得到 LSTM 的输出。由于 ∈[0,1]，tanh(t) ∈ [−1,1]，因此 LSTM 的输出 ∈ [−1,1]。

11.8.5 小结

LSTM 虽然状态向量和门控数量较多，计算流程相对复杂。但是由于每个门控功能清晰明确，每个状态的作用也比较好理解。这里将典型的门控行为列举出来，并解释其代码的 LSTM 行为，如表 11.1 所示。

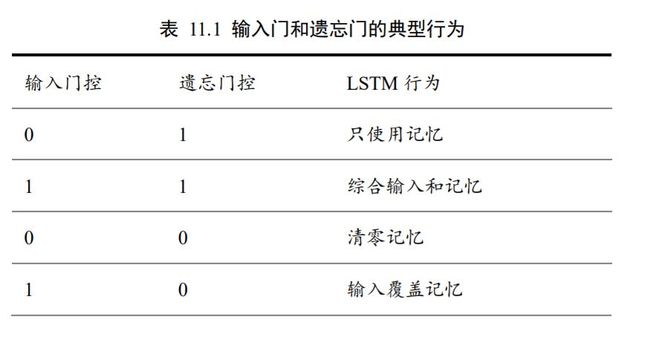
11.9 LSTM 层使用方法

在 TensorFlow 中，同样有两种方式实现 LSTM 网络。既可以使用 LSTMCell 来手动完成时间戳上面的循环运算，也可以通过 LSTM 层方式一步完成前向运算。

11.9.1 LSTMCell

LSTMCell 的用法和SimpleRNNCell 基本一致，区别在于 LSTM 的状态变量 List 有两个，即[ $h_t$, $c_t$]，需要分别初始化，其中 List 第一个元素为 $h_t$，第二个元素为$c_t$。调用 cell完成前向运算时，返回两个元素，第一个元素为 cell 的输出，也就是$h_t$，第二个元素为cell 的更新后的状态 List：[ $h_t$, $c_t$]。首先新建一个状态向量长度ℎ = 64的 LSTM Cell，其中状态向量$c_t$和输出向量$h_t$的长度都为ℎ，代码如下：

x=tf.random.normal([2,80,100])
xt=x[:,0,:]#得到一个时间戳的输入
cell=layers.LSTMCell(64)#创建LSTM Cell
#初始化状态和输出List,[h,c]
state=[tf.zeros([2,64]),tf.zeros([2,64])]
out,state=cell(xt,state)#前向计算
#查看返回元素的id
print(id(out),id(state[0]),id(state[1]))

Out[18]: (1537587122408, 1537587122408, 1537587122728)

可以看到，返回的输出 out 和 List 的第一个元素$h_t$的 id 是相同的，这与基础的 RNN 初衷一致，都是为了格式的统一。

通过在时间戳上展开循环运算，即可完成一次层的前向传播，写法与基础的 RNN 一样。例如：

# 在序列长度维度上解开，循环送入 LSTM Cell 单元
for xt in tf.unstack(x,axis=1):
    #前向计算
    out,state=cell(xt,state)

输出可以仅使用最后一个时间戳上的输出，也可以聚合所有时间戳上的输出向量。

11.9.2 LSTM 层

通过 layers.LSTM 层可以方便的一次完成整个序列的运算。首先新建 LSTM 网络层，
例如：

#创建一层LSTM层，内存向量长度为64
layer=layers.LSTM(64)
#序列通过LSTM层，默认返回最后一个时间戳的输出h
out=layers(x)

经过 LSTM 层前向传播后，默认只会返回最后一个时间戳的输出，如果需要返回每个时间戳上面的输出，需要设置 return_sequences=True 标志。例如：

#创建LSTM层时，内存向量长度为64，设置返回每个时间戳上的输出
layer=layers.LSTM(64,return_sequences=True)
#前向计算，每个时间戳上的输出自动进行了concat，拼成一个张量
out=layer(x)
print(out)

此时返回的 out 包含了所有时间戳上面的状态输出，它的 shape 是[2,80,64]，其中的 80 代表了 80 个时间戳。

对于多层神经网络，可以通过 Sequential 容器包裹多层 LSTM 层，并设置所有非末层网络 return_sequences=True，这是因为非末层的 LSTM 层需要上一层在所有时间戳的输出作为输入。例如：

# 和 CNN 网络一样，LSTM 也可以简单地层层堆叠
net = keras.Sequential([
 layers.LSTM(64, return_sequences=True), # 非末层需要返回所有时间戳输出
 layers.LSTM(64)
])
# 一次通过网络模型，即可得到最末层、最后一个时间戳的输出
out = net(x)

11.10 GRU 简介

LSTM 具有更长的记忆能力，在大部分序列任务上面都取得了比基础的 RNN 模型更好的性能表现，更重要的是，LSTM 不容易出现梯度弥散现象。但是 LSTM 结构相对较复杂，计算代价较高，模型参数量较大。因此，科学家们尝试简化 LSTM 内部的计算流程，特别是减少门控数量。
研究发现，遗忘门是 LSTM 中最重要的门控，甚至发现只有遗忘门的简化版网络在多个基准数据集上面优于标准 LSTM 网络。在众多的简化版 LSTM中，门控循环网络(Gated Recurrent Unit，简称 GRU)是应用最广泛的 RNN 变种之一。GRU把内部状态向量和输出向量合并，统一为状态向量 ，门控数量也减少到 2 个：复位门(Reset Gate)和更新门(Update Gate)，如图 11.19 所示。

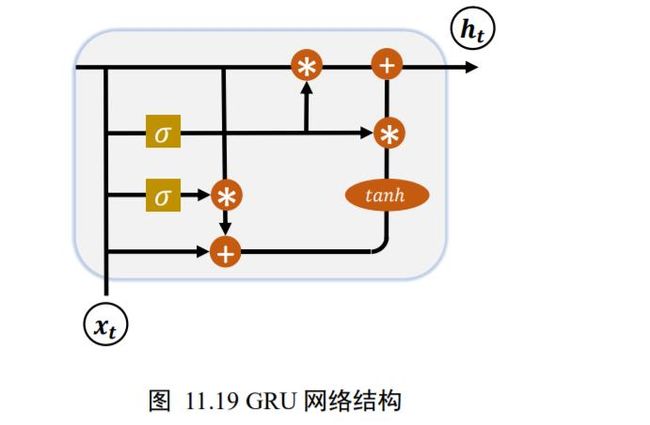
下面我们来分别介绍复位门和更新门的原理与功能。

11.10.1 复位门

复位门用于控制上一个时间戳的状态 $h_{t-1}$进入 GRU 的量。门控向量${\mathbf{g}}_r$由当前时间戳输入$x_t$和上一时间戳状态 $h_{t-1}$变换得到，关系如下：
$${\mathbf{g}}_r=\sigma \left({\mathbf{W}}_r\left[{\mathbf{h}}_{t-1},{\mathbf{x}}_t\right]+{\mathbf{b}}_r\right)$$

其中$w_r$和$b_r$为复位门的参数，由反向传播算法自动优化，为激活函数，一般使用Sigmoid 函数。门控向量${\mathbf{g}}_r$只控制状态$h_{t-1}$，而不会控制输入$x_t$：
$${\mathbf{h}}_t=\tanh \left({\mathbf{W}}_h\left[{\mathbf{g}}_r{\mathbf{h}}_{t-1},{\mathbf{x}}_t\right]+{\mathbf{b}}_h\right)$$

当${\mathbf{g}}_r$= 0时，新输入 ${\mathbf{h}}_t$全部来自于输入$x_t$，不接受 $h_{t-1}$，此时相当于复位$h_{t-1}$。当${\mathbf{g}}_r$= 1时， $h_{t-1}$和输入$x_t$共同产生新输入 ${\mathbf{h}}_t$，如图 11.20 所示。

11.10.2 更新门

更新门用控制上一时间戳状态$h_{t-1}$和新输入 ${\mathbf{h}}_t$对新状态向量$h_t$的影响程度。更新门控向量${\mathbf{g}}_z$由
$${\mathbf{g}}_z=\sigma \left({\mathbf{W}}_z\left[{\mathbf{h}}_{t-1},{\mathbf{x}}_t\right]+{\mathbf{b}}_z\right)$$

得到，其中$w_z$和$b_z$为更新门的参数，由反向传播算法自动优化，为激活函数，一般使用Sigmoid 函数。${\mathbf{g}}_z$用于控制新输入${\mathbf{h}}_t$信号， 1−${\mathbf{g}}_z$用于控制状态 $h_{t-1}$信号：
$${\mathbf{h}}_t=\left(1-{\mathbf{g}}_z\right){\mathbf{h}}_{t-1}+{\mathbf{g}}_z{\mathbf{h}}_t$$

可以看到， ${\mathbf{h}}_t$和$h_{t-1}$对$h_t$的更新量处于相互竞争、此消彼长的状态。当更新门${\mathbf{g}}_z$= 0时， $h_t$全部来自上一时间戳状态$h_{t-1}$；当更新门${\mathbf{g}}_z$ = 1时，$h_t$全部来自新输入 ${\mathbf{h}}_t$。

11.10.3 GRU 使用方法

同样地，在 TensorFlow 中，也有 Cell 方式和层方式实现 GRU 网络。GRUCell和 GRU层的使用方法和之前的 SimpleRNNCell、LSTMCell、SimpleRNN 和 LSTM 非常类似。首先是 GRUCell 的使用，创建 GRU Cell 对象，并在时间轴上循环展开运算。例如：

#初始化状态向量，GRU只有一个
h=[tf.zeros([2,64])]
cell=layers.GRUCell(64)#新建GRU Cell，向量长度为64
#在时间戳维度上解开，循环通过cell
for xt in tf.unstack(x,axis=1):
    out,h=cell(xt,h)
# 输出形状
print(out.shape)

TensorShape([2, 64])

通过 layers.GRU 类可以方便创建一层 GRU 网络层，通过 Sequential 容器可以堆叠多
层 GRU 层的网络。例如：

net = keras.Sequential([
 layers.GRU(64, return_sequences=True),
 layers.GRU(64)
])
out = net(x)

11.11 LSTM/GRU 情感分类问题再战

前面我们介绍了情感分类问题，并利用 SimpleRNN模型完成了情感分类问题的实战，在介绍完更为强大的 LSTM 和 GRU 网络后，我们将网络模型进行升级。得益于TensorFlow 在循环神经网络相关接口的格式统一，在原来的代码基础上面只需要修改少量几处，便可以完美的升级到 LSTM 模型或 GRU 模型。

11.11.1 LSTM 模型

首先是 Cell 方式。LSTM 网络的状态 List 共有两个，需要分别初始化各层的 和向量。例如：

 self.state0 = [tf.zeros([batchsz, units]),tf.zeros([batchsz, units])]
 self.state1 = [tf.zeros([batchsz, units]),tf.zeros([batchsz, units])]

并将模型修改为 LSTMCell 模型。代码如下：

 self.rnn_cell0 = layers.LSTMCell(units, dropout=0.5)
 self.rnn_cell1 = layers.LSTMCell(units, dropout=0.5)

其它代码不需要修改即可运行。

对于层方式，只需要修改网络模型一处即可，修改如下：

 # 构建 RNN，换成 LSTM 类即可
 self.rnn = keras.Sequential([
 layers.LSTM(units, dropout=0.5, return_sequences=True),
 layers.LSTM(units, dropout=0.5)
 ])

11.11.2 GRU 模型

首先是 Cell 方式。GRU 的状态 List 只有一个，和基础 RNN 一样，只需要修改创建Cell 的类型，代码如下：

 # 构建 2 个 Cell
 self.rnn_cell0 = layers.GRUCell(units, dropout=0.5)
 self.rnn_cell1 = layers.GRUCell(units, dropout=0.5)

对于层方式，修改网络层类型即可，代码如下：

 # 构建 RNN
 self.rnn = keras.Sequential([
 layers.GRU(units, dropout=0.5, return_sequences=True),
 layers.GRU(units, dropout=0.5)
 ])

11.12 预训练的词向量

在情感分类任务时，Embedding 层是从零开始训练的。实际上，对于文本处理任务来说，领域知识大部分是共享的，因此我们能够利用在其它任务上训练好的词向量来初始化Embedding 层，完成领域知识迁移。基于预训练的 Embedding 层开始训练，少量样本时也能取得不错的效果。

我们以预训练的 GloVe 词向量为例，演示如何利用预训练的词向量模型提升任务性能。首先从官网下载预训练的 GloVe 词向量表，我们选择特征长度 100 的文件glove.6B.100d.txt，其中每个词汇使用长度为 100 的向量表示，下载后解压即可。

利用 Python 文件 IO 代码读取单词的编码向量表，并存储到 Numpy 数组中。代码如下：

print('Indexing word vectors.')
embeddings_index={}#提取单词及其向量，保存在字典中
# 词向量模型文件存储路径
GLOVE_DIR=r'D:\pycharm\Test\test\glove.6B.100d.txt'
with open(os.path.join(GLOVE_DIR,'glove.6B.100d.txt'),encoding='utf-8')as f:
    for line in f:
        values=line.split()
        word=values[0]
        coefs=np.asarray(values[1:],dtype='float32')
        embeddings_index[word]=coefs
print('Found %s word vectors.'% len(embeddings_index))

GloVe.6B 版本共存储了 40 万个词汇的向量表。前面实战中我们只考虑最多 1 万个常见的词汇，我们根据词汇的数字编码表依次从 GloVe 模型中获取其词向量，并写入对应位置。代码如下

num_words = min(total_words, len(word_index))
embedding_matrix = np.zeros((num_words, embedding_len)) #词向量表
for word, i in word_index.items():
 if i >= MAX_NUM_WORDS:
 continue # 过滤掉其他词汇
 embedding_vector = embeddings_index.get(word) # 从 GloVe 查询词向量
 if embedding_vector is not None:
 # words not found in embedding index will be all-zeros.
 embedding_matrix[i] = embedding_vector # 写入对应位置
print(applied_vec_count, embedding_matrix.shape)

在获得了词汇表数据后，利用词汇表初始化 Embedding 层即可，并设置 Embedding 层不参与梯度优化。代码如下：

 # 创建 Embedding 层
 self.embedding = layers.Embedding(total_words, embedding_len,
 input_length=max_review_len,
trainable=False)#不参与梯度更新
 self.embedding.build(input_shape=(None, max_review_len))
 # 利用 GloVe 模型初始化 Embedding 层
 self.embedding.set_weights([embedding_matrix])#初始化

其它部分均保持一致。我们可以简单地比较通过预训练的 GloVe 模型初始化的 Embedding层的训练结果和随机初始化的 Embedding 层的训练结果，在训练完 50 个 Epochs 后，预训练模型的准确率达到了 84.7%，提升了约 2%。

11.13 参考文献

[1] I. Goodfellow, Y. Bengio 和 A. Courville, Deep Learning, MIT Press, 2016.
[2] J. Westhuizen 和 J. Lasenby, “The unreasonable effectiveness of the forget gate,” CoRR,
卷 abs/1804.04849, 2018.