python机器学习之异常检测与主成分分析
前言
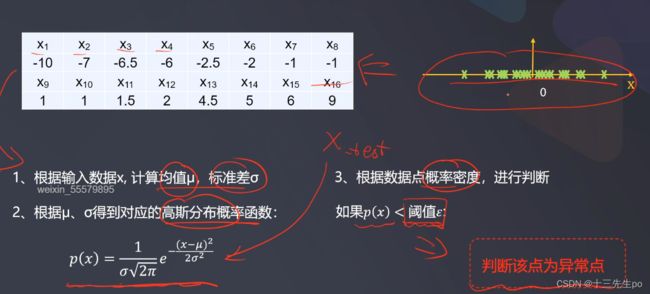
- 根据输入数据，对不匹配预期模式的数据进行识别
检测分类
-
监督式异常检测：提前使用带“正常”与“异常”标签的数据对模型进行训练，机器基于训练好的模型判断新数据是否为异常数据
-
无监督式异常检测：通过寻找与其他数据最不匹配的实例来检测出未标记测试数据的异常
检测原理
- 基于数据分布，寻找与其他数据最不匹配的实例，寻找发生可能性低的数据（事件）
- 概率是一个在0到1之间的实数，是对随机事件发生可能性的度量，反映某种情况出现的可能性（likelihood)大小。
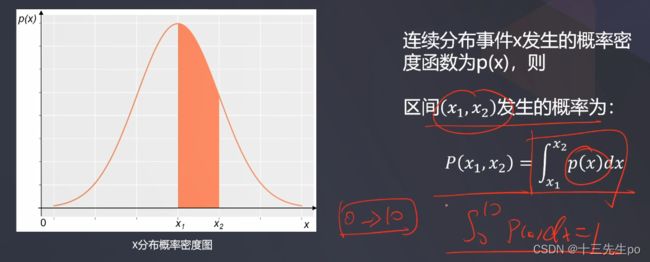
- 在连续分布事件中，用于描述连续随机变量的输出值在某个确定的取值点附近的可能性的函数，通过其可计算取值点附近区间发生事件的概率。（正态分布）
实战：异常消费行为检测
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
- 读取数据
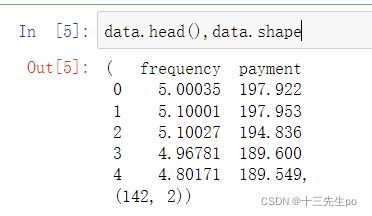
# 读取数据
data = pd.read_csv('task1_data.csv')
data.head(),data.shape
- 数据可视化
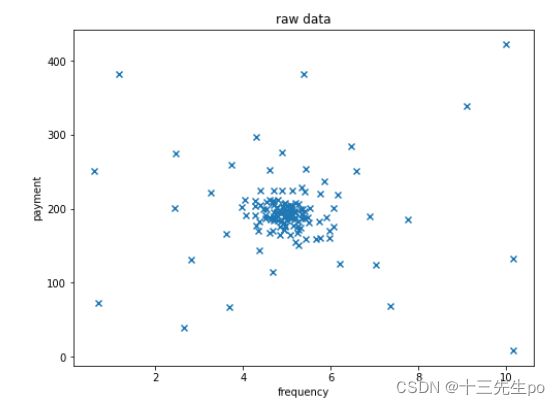
# 数据可视化
fig1 = plt.figure(figsize=(8,6))
plt.scatter(data.loc[:,'frequency'],data.loc[:,'payment'],marker='x')
plt.title('raw data')
plt.xlabel('frequency')
plt.ylabel('payment')
plt.show()
- 数据赋值
# 数据赋值
x1 = data.loc[:,'frequency']
x2 = data.loc[:,'payment']
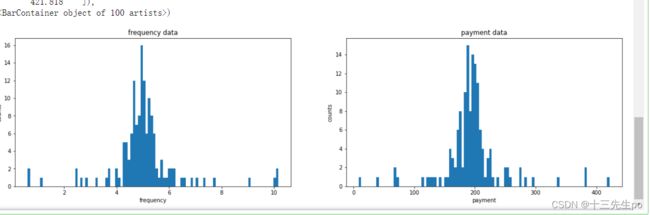
# 数据分布频次图
fig2 = plt.figure(figsize=(20,5))
fig2_1 = plt.subplot(121)
plt.title('frequency data')
plt.xlabel('frequency')
plt.ylabel('counts')
plt.hist(x1,bins=100)
fig2_2 = plt.subplot(122)
plt.title('payment data')
plt.xlabel('payment')
plt.ylabel('counts')
plt.hist(x2,bins=100)
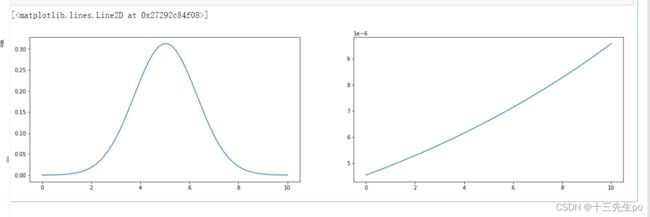
- 计算数据均值，标准差，绘制高斯分布图
fig5 = plt.figure(figsize=(20,5))
fig5_1 = plt.subplot(121)
# 计算数据均值，标准差
# 均值
x1_mean = x1.mean()
# 标准差
x1_std = x1.std()
# 计算对应的高斯分布数值：
from scipy.stats import norm
# 生成0-10区间的三百个点
x1_range = np.linspace(0,10,300)
# 生成分布区间对应的关键参数
normal1 = norm.pdf(x1_range,x1_mean,x1_std)
# 可视化高斯分布曲线
plt.plot(x1_range,normal1)
'''第二张'''
fig5_2 = plt.subplot(122)
# 计算数据均值，标准差
# 均值
x2_mean = x2.mean()
# 标准差
x2_std = x2.std()
# 计算对应的高斯分布数值：
from scipy.stats import norm
# 生成0-10区间的三百个点
x2_range = np.linspace(0,10,300)
# 生成分布区间对应的关键参数
normal2 = norm.pdf(x2_range,x2_mean,x2_std)
# 可视化高斯分布曲线
plt.plot(x2_range,normal2)
- 生成用于绘制3D高斯分布图的数据
#生成用于绘制3D高斯分布图的数据
import math
#设置范围
x_min, x_max = 0, 10
y_min, y_max = 0, 400
h1 = 0.1
h2 = 0.1
#生成矩阵数据
xx, yy = np.meshgrid(np.arange(x_min, x_max, h1), np.arange(y_min, y_max, h2))
print(xx.shape,yy.shape)
#展开矩阵数据
x_range = np.c_[xx.ravel(), yy.ravel()]
x1 = np.c_[xx.ravel()]
x2 = np.c_[yy.ravel()]
x_range_df = pd.DataFrame(x_range)
#x_range_df.to_csv('data.csv')
#高斯分布参数
u1 = x1_mean
u2 = x2_mean
sigma1 = x1_std
sigma2 = x2_std
#计算高斯分布概率
p1 = 1/sigma1/math.sqrt(2*math.pi)*np.exp(-np.power((x1-u1),2)/2/math.pow(sigma1,2))
p2 = 1/sigma2/math.sqrt(2*math.pi)*np.exp(-np.power((x2-u2),2)/2/math.pow(sigma2,2))
p = np.multiply(p1,p2)
#对概率密度维度转化
p_2d = p.reshape(xx.shape[0],xx.shape[1])
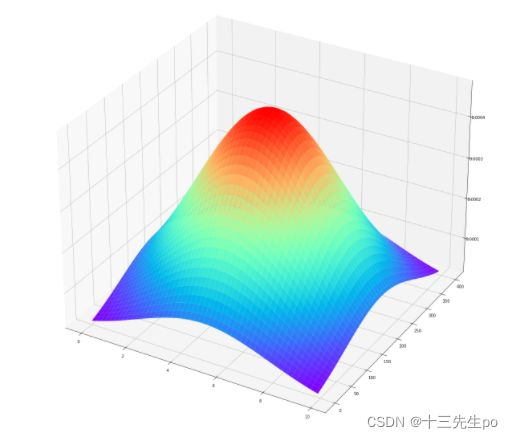
# 3D高斯分布概率密度函数图形可视化
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig3 = plt.figure(figsize=(16,16))
axes3 = Axes3D(fig3)
axes3.plot_surface(xx,yy,p_2d,cmap=cm.rainbow)
- 模型建立以及训练
# 模型建立以及训练
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope(contamination=0.03)
ad_model.fit(data)
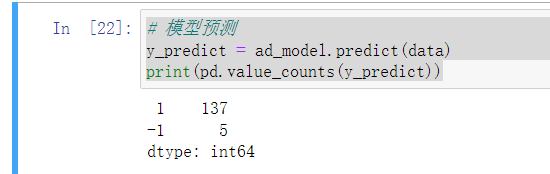
- 模型预测
# 模型预测
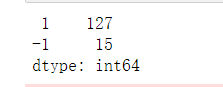
y_predict = ad_model.predict(data)
print(pd.value_counts(y_predict))
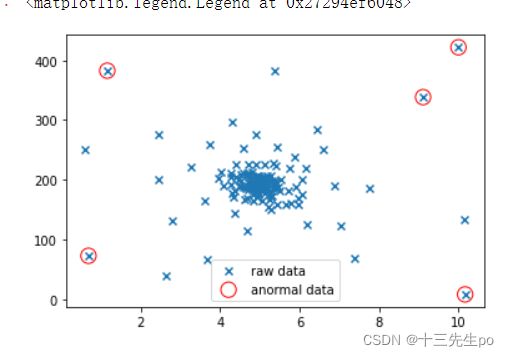
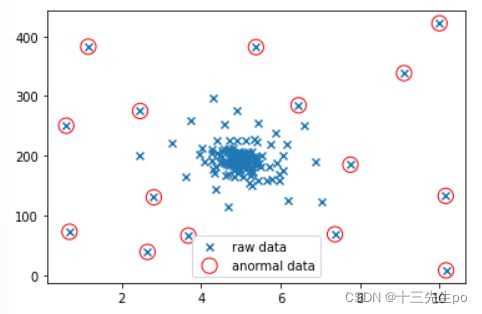
- 正常的数据和异常数据可视化
# 正常的数据可视化
nomal_data = plt.scatter(data.loc[:,'frequency'],
data.loc[:,'payment'],
marker='x',
edgecolor='blue',
label = 'raw data'
)
# 异常数据可视化
anomal_data = plt.scatter(data.loc[:,'frequency'][y_predict==-1],
data.loc[:,'payment'][y_predict==-1],
marker='o',
facecolor='none',
edgecolor='red',
s=150,label = 'anormal data')
plt.legend()
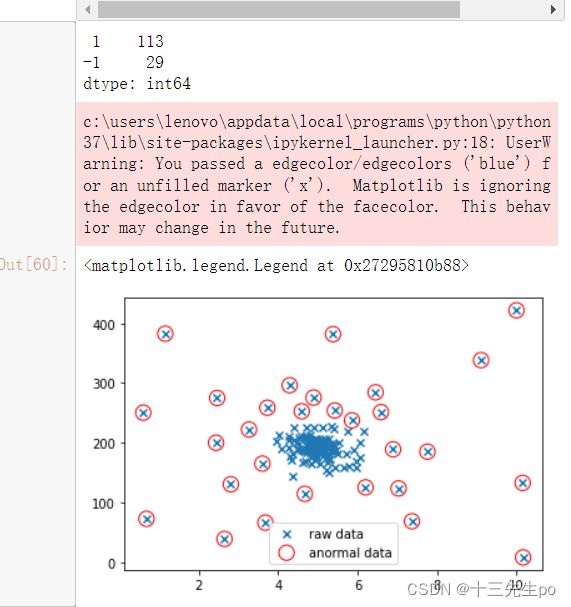
- 修改不同阈值得出的异常数据
contamination=0.1
# 模型建立以及训练
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope(contamination=0.1)
ad_model.fit(data)
# 模型预测
y_predict = ad_model.predict(data)
print(pd.value_counts(y_predict))
# 正常的数据可视化
nomal_data = plt.scatter(data.loc[:,'frequency'],
data.loc[:,'payment'],
marker='x',
edgecolor='blue',
label = 'raw data'
)
# 异常数据可视化
anomal_data = plt.scatter(data.loc[:,'frequency'][y_predict==-1],
data.loc[:,'payment'][y_predict==-1],
marker='o',
facecolor='none',
edgecolor='red',
s=150,label = 'anormal data')
plt.legend()
筛选出的异常值变多了
contamination=0.2时
# contamination=0.2
# 模型建立以及训练
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope(contamination=0.2)
ad_model.fit(data)
# 模型预测
y_predict = ad_model.predict(data)
print(pd.value_counts(y_predict))
# 正常的数据可视化
nomal_data = plt.scatter(data.loc[:,'frequency'],
data.loc[:,'payment'],
marker='x',
edgecolor='blue',
label = 'raw data'
)
# 异常数据可视化
anomal_data = plt.scatter(data.loc[:,'frequency'][y_predict==-1],
data.loc[:,'payment'][y_predict==-1],
marker='o',
facecolor='none',
edgecolor='red',
s=150,label = 'anormal data')
plt.legend()
随着阈值的增大，异常值也在变多
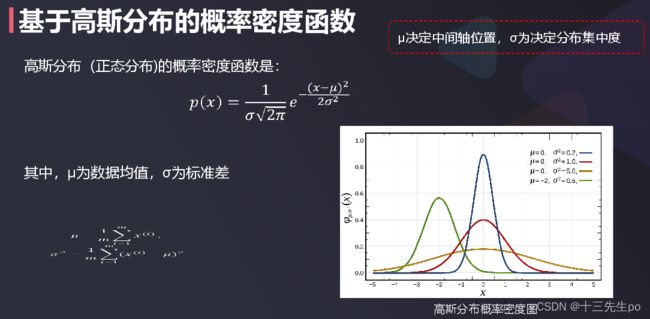
基于高斯分布的概率密度函数
- 概率论中最重要的分布
现实生活中，很多事件发生的频率都符合高斯分布，比如：工业产品的强力、抗压强度、口径、长度等指标；人体的身高、体重等指标；同一品种种子的重量；某个地区的年降水量，等等。
- μ决定中间轴位置，σ为决定分布集中度
- 计算示例（手误，3.5的平方≠7）
- 计算出结果后，这时候给一个测试数据x_test就能出结果
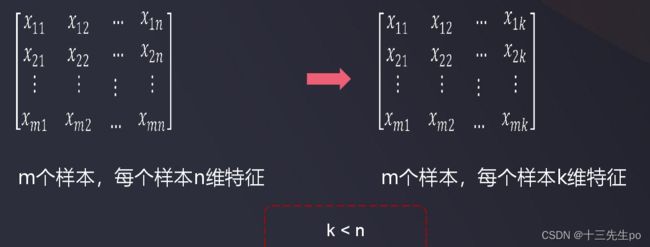
多维度数据处理
- 当数据维度高于一维时
- 计算示例
数据降维
-
简化机器学习框架
想建立一个AI模型，筛选金融股票，
潜在数据指标：
价格、交易量、换手率、股东人数、最近N日
涨跌幅、RSI指标、威廉指标、市值、营业额、
净利润、负债率、利润增长率…多达几百、上千个因子，这时就有有两大问题：求解困难、模型过拟合 -
在一定的限定条件下，按照一定的规则，尽可能保留原始数据集重要信息的同时，降低数据集特征的个数。
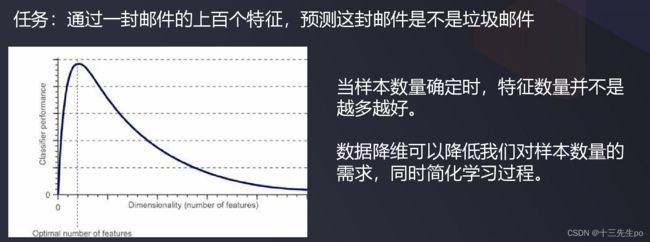
为什么需要数据降维
- 维数灾难
随着特征数量越来越多，为了避免过拟合，对样本数量的需求会以指数速度增长。
- 数据可视化
高维数据不能可视化，只有降低到二维或三维才能可视化。
例如3D数据降维到2D数据
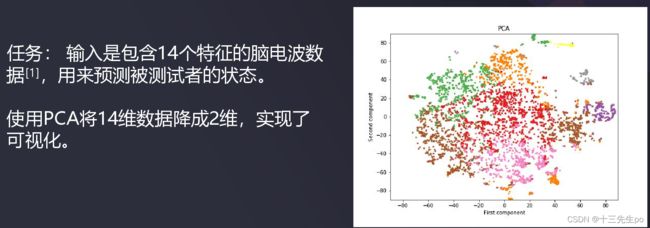
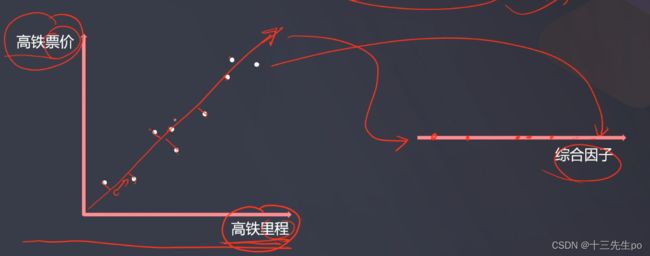
数据降维最常用的方法：主成分分析（PCA)
也称主分量分析，按照一定规则把数据变换到一个新的坐标系统中（如图中的红线），使得任何数据投影后尽可能可以分开（新数据尽可能不相关、分布方差最大化）。
核心点：投影后的数据尽可能分得开（即不相关）
- 如何实现：使投影后数据的方差最大，因为方差越大数据也越分散
- 计算过程：
- 数据预处理
标准化有重要意义，假如有数值是在10-20之间，而有些数是在10万——100万之间，这时候计算出来的数据中，10-20之间的数就会变成相对小的数值可能会被忽略，影响太小了
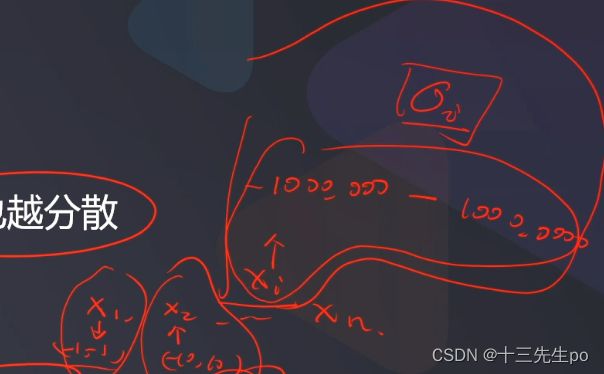
- 计算协方差矩阵特征向量、及数据在各特征向量投影后的方差
协方差矩阵参考资料：
https://blog.csdn.net/dfly_zx/article/details/107908497
3. 根据需求（任务指定或方差比例）确定降维维度k
- 任务指定就是有一个明确的目标（直接提出的业务需求，将xx维度降到维度k）
- 方差比例：计算得出的各主成分方差，同时输出方差的重要比例，计算方差比例之和，如果基本等于1，说明数据没有太大的丢失；否则说明有很多数据丢失了，说明降的维度不合适
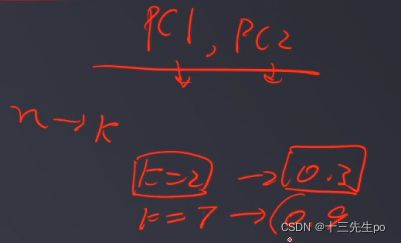
- 选取k维特征向量，计算数据在其形成空间的投影
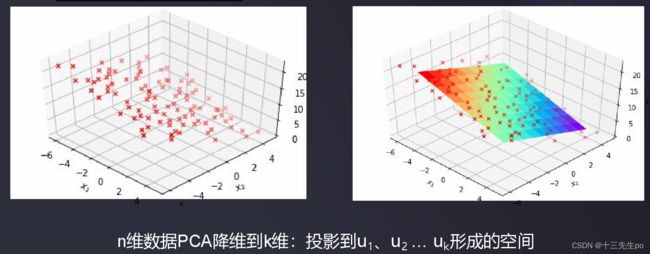
- 案例。n维数据PCA降维到k维：投影到u1、u2 … uk形成的空间
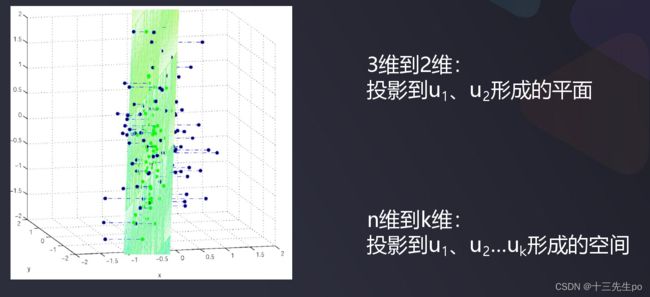
3维数据PCA降维到2维：投影到u1、u2形成的平面
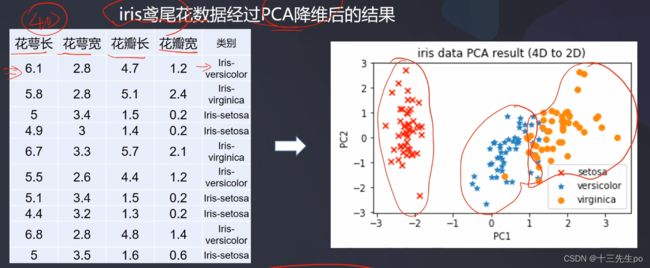
iris鸢尾花数据经过PCA降维后的结果
实战：PCA+逻辑回归预测检查者是否患糖尿病
将降维前的数据模型和降维后的数据模型进行对比准确率
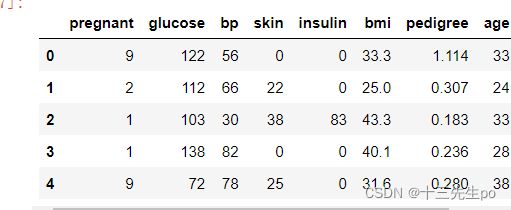
# 导入数据
data2 = pd.read_csv('task2_data.csv')
data2.head()
- 数据赋值
# 数据赋值
x3 = data2.drop(['label'],axis=1)
y3 = data2.loc[:,'label']
- 建立逻辑回归模型
# 建立逻辑回归模型
from sklearn.linear_model import LogisticRegression
# 如果报警告STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.，指的是最大迭代次数超出默认限制=300，这时候其实模型可能还没训练完成
# 设置最大的跌打次数max_iter
model2 = LogisticRegression(max_iter=1000)
model2.fit(x3,y3)
- 结果预测
# 结果预测
y3_predict = model2.predict(x3)
print(y3_predict)
- 模型评估
# 模型评估
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y3,y3_predict)
print(accuracy)
- 数据标准化（后期降维用）
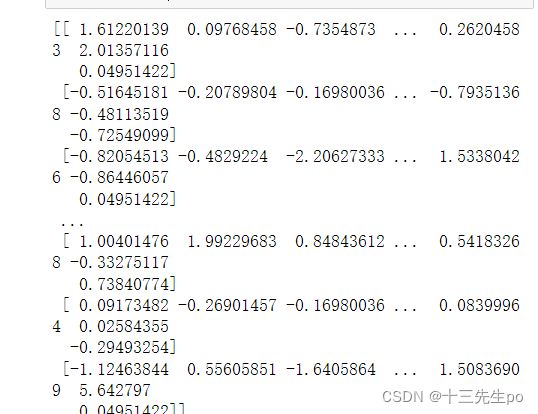
# 数据标准化
from sklearn.preprocessing import StandardScaler
x_norm = StandardScaler().fit_transform(x3)
print(x_norm)
取第2列（即坐标=1）的所有值（用于验证标准化是否正确）
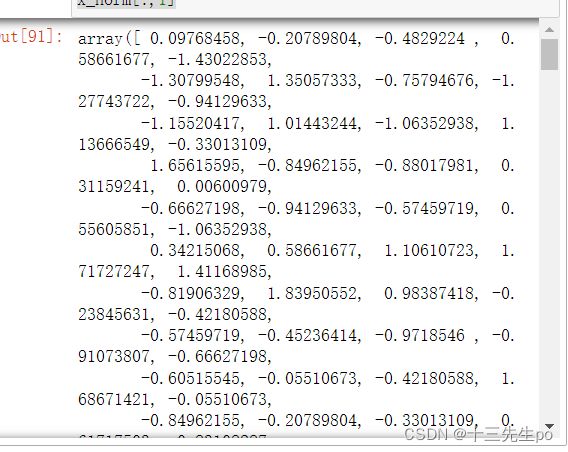
# 取第2列（即坐标=1）的所有值
x_norm[:,1]
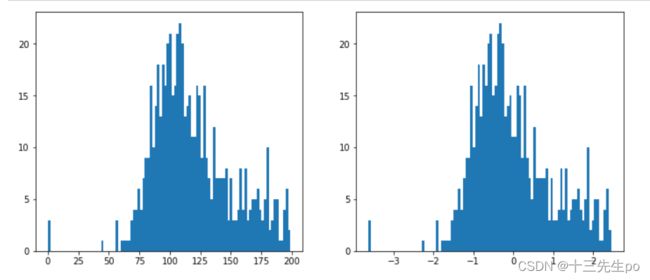
- 标准化前后可视化
# 标准化前后可视化
fig = plt.figure(figsize=(12,5))
fig_1 = plt.subplot(121)
plt.hist(x3.loc[:,'glucose'],bins=100)
fig_2 = plt.subplot(122)
plt.hist(x_norm[:,1],bins=100)
plt.show()
- pca分析降到8维
对于比例占比，如果前两个维度的占比和接近0.8-0.9，可能信息都很足够了，但并不是说不到0.8就不行，需要具体情况具体分析，看对结果有影响的重要信息是否有保留下来
# pca分析
from sklearn.decomposition import PCA
# 修改目标维度值
pca = PCA(n_components=8)
x_pca = pca.fit_transform(x_norm)
# 计算各成分投影数据方差
var = pca.explained_variance_
# 计算各成分投影数据方差的比例
# var_ratio中各值的和＝1，因为是比例
# 对于比例占比，如果前两个维度的占比和接近0.8-0.9，
# 可能信息都很足够了，但并不是说不到0.8就不行，需要具体情况具体分析，看对结果有影响的重要信息是否有保留下来
var_ratio = pca.explained_variance_ratio_
print(var)
print(var_ratio)
print(sum(var_ratio))
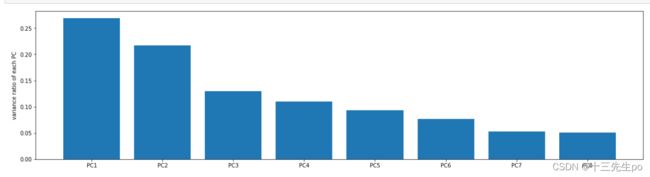
- 可视化方差比例
# 可视化方差比例
fig4 = plt.figure(figsize=(20,5))
plt.bar([1,2,3,4,5,6,7,8],var_ratio)
plt.xticks([1,2,3,4,5,6,7,8],
['PC1','PC2','PC3','PC4','PC5','PC6','PC7','PC8'])
plt.ylabel('variance ratio of each PC')
plt.show()
- 降维后的模型建立与训练
# 降维后的模型建立与训练
model4 = LogisticRegression()
model4.fit(x_pca,y3)
- 模型预测
# 模型预测
y_predict_pca8 = model4.predict(x_pca)
accuracy_pca8 = accuracy_score(y_predict_pca8,y3)
print(accuracy_pca8)
- 降到2维
数据降到2维
# 数据降到2维
pca2 = PCA(n_components=2)
x_pca2 = pca2.fit_transform(x_norm)
x_pca2.shape
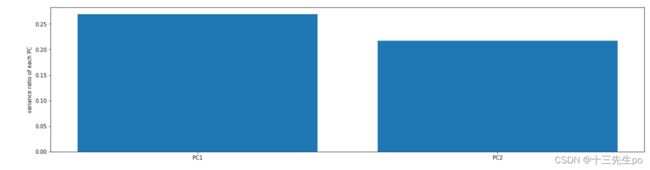
- 可视化方差比例
var2_ratio = pca2.explained_variance_ratio_
# 可视化方差比例
fig4 = plt.figure(figsize=(20,5))
plt.bar([1,2],var2_ratio)
plt.xticks([1,2],
['PC1','PC2'])
plt.ylabel('variance ratio of each PC')
plt.show()
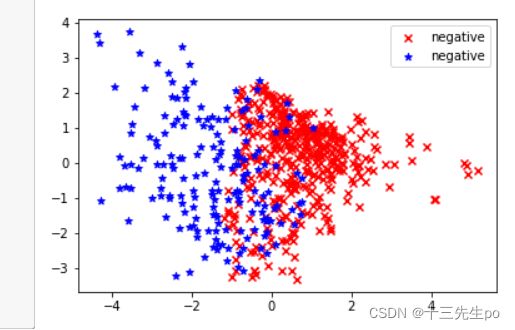
- 可视化降维数据（只有降到2维或3维才能将数据可视化）
# 可视化降维数据
negative = plt.scatter(x_pca2[:,0][y3==0],
x_pca2[:,1][y3==0],
c='r',marker='x',
label='negative')
negative = plt.scatter(x_pca2[:,0][y3==1],
x_pca2[:,1][y3==1],
c='b',marker='*',
label='negative')
plt.legend()
- 降维后的模型建立与训练
# 降维后的模型建立与训练
model3 = LogisticRegression()
model3.fit(x_pca2,y3)
- 模型预测准确率
# 模型预测
y_predict_pca2 = model3.predict(x_pca2)
accuracy_pca2 = accuracy_score(y_predict_pca2,y3)
print(accuracy_pca2)
