C语言递归单链表反转,C语言之单链表反转(递归,迭代),排序
C语言之单链表反转(递归,迭代),排序
前言
这篇会是关于单链表最后一篇的介绍,之前还介绍过的文章分别是:
单链表及各项操作介绍
单链表初始化
单链表打印(遍历),查询,定位,插入,删除,链表长度
单链表反转,排序,即本文
单链表反转之迭代
对于单链表很多的基本算法,甚至是树结构,在这本人都比较建议各位不要用大脑想如何实现,而是在本子上画出来它的步骤,即使是个大概也好,必须先要有思路再敲代码。所以在这里先用图解来介绍一下单链表反转中运用迭代的方式实现的步骤。
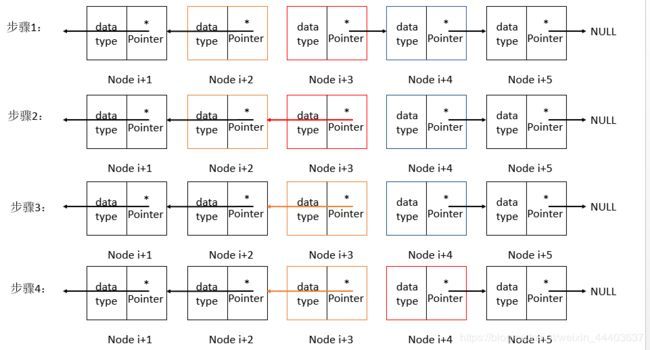
首先我们先取单链表当中的任意一个节点来作例子:
从上面的图片可以看出来,想要完成链表之间的反转,必须要同时记录三个节点的位置。听上去有点繁琐,不过这也是在迭代方式中不可避免条件。
在这三个记录当中,中节点(红色框)是我们目前想要把其指针域指反转的对象。前节点(橙色框)是将要被指向的对象。而后节点(蓝色框)是下一个将要反转的对象。
其中之所以需要记录前节点的位置是因为对于单链表来说,它是永远都不会知道指向自己的节点的位置是在哪里,为了达到反转的目的,我们必须时刻保存前节点的位置来告知当前节点必须指向的位置。
而对于后节点来说,因为我们必须要把中节点的指针域改成指向前节点,如果这个时候我们没有任何后节点的信息,那么我们便实行不了下一步的反转了。所以可以看到,当步骤4执行完之后,其实它的下一步就是回到步骤1了。
所以迭代反转的步骤是:
定义前节点
定义后节点
当前节点(中节点)指针域指向前节点
前节点等于中节点(步骤1)
中节点等于后节点
回到步骤2
以上叙述都是对于一个链表中的任一节点,那么如何开始是我们值得思考的下一个问题。
从上面的图片可以看出来,对于header来说,一没有前节点,二它应该指向单链表尾部的最后一个节点。
对于这样的问题有两个思路,一就是把前节点定义成 Node3(这个单链表最后一个节点)。不过这样也有问题。一就是我们不知道最后一个节点的位置,不过也许有人会想,通过一次遍历就好了。这样也ok,不过再细想下一步,当Node1需要反转的时候,它应该要指向NULL,或者是有数据域的节点,而不是头节点header。
所以这样就要用到第二个思路了:
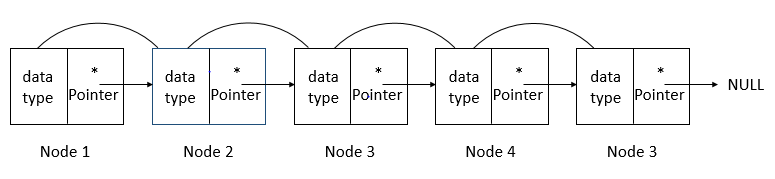
从以上图片看出来,我们第一步就是先把header给单独记录下来,(这样的话,就是同时有4个节点被记录了:header,前中后节点)。这样做可以把第一个思路的第二个问题给解决掉了。不过思路一的第一个问题还在。前节点到底是什么呢。刚才我们说把Node3定义为前节点原因是它是这个链表的最后一个节点,这么理解也可以,不过其实我们忽略了一个至关重要的节点,那就是NULL:
从上图中的单链表等价于我们之前的链表,唯一有变动的就是把NULL也比作成了一个节点。这样的话我们单链表反转就可以开始进行的了。
然后最后一个需要思考的问题就是什么时候停止。相信看过之前文章的都能看出来,当当前节点(中节点)为空的时候,那么反转的步骤就可以停止了。
然后因为我们的尾节点Node3被前节点给保存下来了,所以最后我们只需要把header指针域改成指向前节点即可。
具体实现代码如下:
//单链表递归反转
void f6(node** head) {
printf("单链表反转结果为:\n");
node* p = _reverse((*head)->next);
(*head)->next = p;
_print(*head);
}
根据上述已经总结的步骤:
定义前节点
定义后节点
当前节点(中节点)指针域指向前节点
前节点等于中节点
中节点等于后节点
回到步骤2
//单链表反转
node* _reverse(node* q) {
node* pre = NULL;//1.定义前节点
while (q) {
node* nex = q->next;//2.定义后节点
q->next = pre; //3.单链表反转
pre = q;//4.定义前节点
q = nex;//5.定义当前节点
}
return pre;
单链表反转之递归
我们已经有了以上的迭代的经验了,对于递归,我们可以直接从把header 跟单链表先分开,这样有利于对链表内容进行操作:
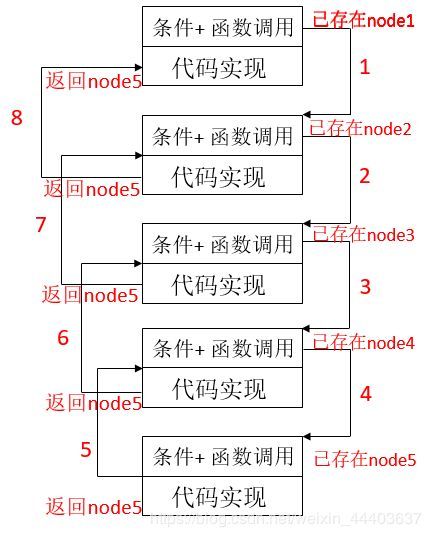
递归其实就是函数本上调用自身,当遇到一定条件时停止(个人理解)。所以在考虑用递归时,我们第一步该想到的是什么时候停止使用递归。而停止使用递归其实往往就是迭代的最后一步,然后就可以把单链表从后往前修改。这么说可能不太清楚这函数是怎么调用的,以下图片特意解释递归的流程:
根据上图,可以看出来一个有5个函数被调用了,而这5个函数其实都是一样的,所以说它正在调用自身。函数的第一部分为条件。根据我们所说的,一般调用到当前节点为此链表最后一个节点时才会停止调用自身。所以以上流程1至4如下:
当前node1,调用参数为node2的函数
当前node2,调用参数为node3的函数
当前node3,调用参数为node4的函数
当前node4,调用参数为node5的函数,因为node5为最后一个节点,直接结束此函数,执行返回。
代码:
if (q == NULL || q->next == NULL)
return q;
node* p = _reverse(q->next);
代码实现部分:实行后节点指向当前节点。
这时有人可能会问,为什么在递归当中我们不用像迭代一样保存前中后三个节点。在回答问题之前,首先要看看,既然我们没有保存三个节点,那么我们保存了哪几个节点呢。答案是两个,分别是当前节点和前节点。可以看出来每个函数,它自身本来就存在当前节点,这个是毫无疑问的,而前节点又被保存在哪里呢?这个前节点其实就被保存在这个函数被调用前的函数里头(希望这样能够理解)。就是说,函数4的前节点其实就是函数3的当前节点。
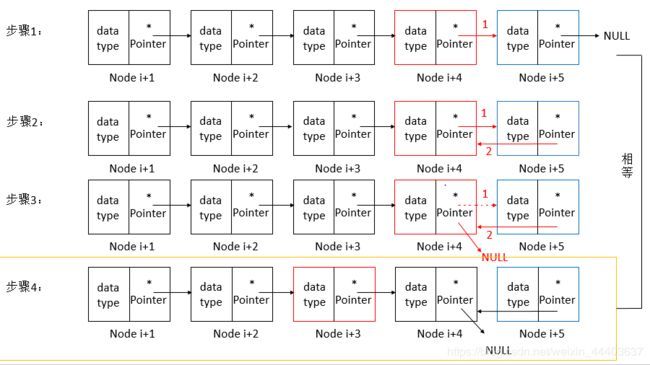
至于为什么不需要后节点了,那是因为,我们采用了递归是一种从后往前修改的一种方式:迭代是从前往后修改,迭代之所以需要保存前节点,那是因为我们当前节点不知道前节点地址,而递归从后往前,后节点能够通过指针域访问。相关流程图如下:
步骤:
后节点指向当前节点
当前节点指向NULL
q->next->next = q;//1. 后节点指向当前节点
q->next = NULL;//2. 当前节点指向NULL
return p;
最后需要探讨的就是,返回值。对于函数返回值,我们希望返回链表反转后成为第一个的节点,这样的话header就可以直接指向它了,所以说应该返回原链表的尾节点。
递归总概述:
//单链表反转
node* _reverse(node* q) {
if (q == NULL || q->next == NULL) return q;
node* p = _reverse(q->next);
q->next->next = q;
q->next = NULL;
return p;
题外话
递归是一种比较普遍的算法。与递归结合的数据结构叫做栈(stack)。我记得之前有一次面试,考官问我什么是栈,什么是堆,区别在哪里。当时的会答是,栈是一种先进后出的数据结果,而堆是一种先进先出的数据结构。栈的例子主要有递归,word文档打字时的撤回。而堆就像排队,售票系统应用。
泡沫排序
排序算法有很多,其中泡沫排序是最基础的算法。冒泡排序就是两两相邻的两个节点相比较,按从小到大的方式排序,如果后节点比前节点大则不作任何修改,反之其数据域里的数值互换。等遍历完整条单链表后继续,重复单链表长度的次数为止,那么得出的单链表一定是按照从小到大排序的。
这样的排序复杂度为: O(n^2)
不过这个算法也可以被修改,倘若一次遍历过程没有发生任何数据互换的情况,说明了单链表的顺序已经被提前排序好了,所以之后的遍历都没有任何意义。所以在进行这个算法时,往往都会在遍历过程中有一个计数记录数值互换次数,当遍历完成后会重置成0。若某次遍历完后,计数仍然为0的话,则表示此次遍历没有发生任何数值互换,所以说明排序已经完成了,这样就可以提前跳出循环来节约时间。
在最理想情况下,遍历只发生一次。不过在编程中都是考量最坏情况下的时间复杂度,所以最坏情况下,遍历还是会发生n次,所以其时间复杂度依旧没有任何改变。
代码:
//排序
void f7(node** head) {
printf("链表排序后结果为:\n");
_queue(*head);
_print(*head);
}
void _queue(node* head) {
for (node* p = head->next; p->next != NULL; p = p->next) {
int flag = 0;
for (node* q = head->next; q->next != NULL; q = q->next) {
if (q->value > q->next->value) {
int t = q->value;
q->value = q->next->value;
q->next->value = t;
flag++;
}
}
if (flag == 0)break;
}
}
结语
目前为止,关于单链表的各项操作都已经粗略的介绍过了一遍,不过单链表还有很多变型的题目是面试的考点。这需要平常多上网页上刷题训练。 除了C语言外,我还有用C++实现的单链表代码,主要是为了锻炼使用对象和类的能力,会在之后一篇博文上发布,不过不会有太多的讲解了。
除此之外,我还用C++实现了二叉查找树和平衡二叉树的各项操作。在这谈谈心得吧。其实一开始觉得树应该是最难的,不过我人认为,单链表是最难的。因为对于刚接触单链表的我,对于结构体是非常不熟悉的,不过等我把单链表用C和C++都实现了一遍之后,发现树结构也不过如此。大概是因为树其实只是链表的一种延伸罢了。无论做什么都好,基础最重要,不要觉得总是捉一些简单的知识来学没用。很多时候,其实我们连最简单的都不一定会呢。
对于二叉查找树和平衡二叉树的代码,我也会在之后的文章上发布,不过一样也不会用太多的文字来讲解了。
不是博主懒,而是博主下一系列的文章内容结构将会非常的庞大——通信原理之信道编码仿真MATLAB。
通信原理是我本科和硕士的课程,日久生情了吧,还觉得挺有意思的。其中主要实现hamming码和卷积码。卷积码又是重中之中,因为4G就会涉及到卷积码的延伸。想学习5G,4G又是很重要的基础。
对了,不在是C和C++了,而是MATLAB语言,可能是因为前段时间敲C敲乏味了,想换换,但是MATLAB还是跟C很相似的。不过之后也会在有空的时候发发C相关零散的文章吧。