ogldev-读书笔记

主要是记录一些比较特别的要点。
一.矩阵乘法
1.注意矩阵乘法用左乘还是右乘，因为程序如果用类似堆栈的方式来实现的话是后进先出的，所以和一般乘法不同的是，右乘是从右边开始计算，如：
ABC 是先计算C矩阵乘以B，结果再乘以A。
而且是不满足乘法交换律的ABC的结果不等于CBA。如：先位移再旋转和先旋转再位置结果是不一样的，因为旋转是以坐标原点来作为旋转点的。所以一般计算时，都是先做完旋转和缩放，最后再进行位移操作。

2.留意存储矩阵时，是按照行优先储存还是列优先存储，不同的存储方式，计算出来的结果也不一样。

二.欧拉相机
1.通过角度(FOV)、近裁切面(nearz)、远裁切面(farz)、屏幕大小，4个参数，可以把相机前的3D物体投射显示到2D屏幕上，而且忽略了大量不必要的渲染，如：比远裁切面更远的不渲染、比近裁切面更近的不渲染、裁切面4条边范围以外的不渲染。
2.通过分别对X,Y,Z轴逐一旋转的方式,让欧拉相机360度无死角的显示。
3.静态欧拉角：绕世界坐标系的X,Y,Z轴来进行旋转。旋转过程中坐标轴保持静止，所以是静态 。
动态欧拉角：绕物体坐标系的X,Y,Z轴来进行旋转。旋转过程中坐标轴会跟着物体一起旋转，所以是动态。（会有经典的万向锁问题）

三.万向锁
欧拉角主要是通过依次旋转3轴。当旋转中间层到±90度时，第一层会和第三层重叠（轴心相同），第一层和第三层的旋转结果等价，就会失去了一个维度的旋转控制。
解决方案：把原来的3元素改成使用4元素来计算。

四.UVN相机
相对于欧拉相机通过角度来定义相机朝向，UVN相机使用的是向量。
n: 视觉方向向量，相当于z轴。
v:上向量
u:右向量
t:相机注视的目标点(target)
e:相机位置(eye)
计算UVN向量的过程：

1. n = t - e
2. 假设v向量为<0, 1, 0>，就可以统计叉乘计算得 u = v * n
3. 得到u后，就可以计算出 v = n * u
4. 最后把计算所得的uvn进行单位化即可。
   接下来就是要把目标物的坐标从世界坐标转换为相机坐标（视觉坐标）。
   
   如上图，假设初始相机坐标和世界坐标一致（完全重合），然后通过4步变换，把目标坐标转换为相机坐标。
   1.把相机旋转到能对准目标的角度。
   2.把相机平移到对准目标。
   PS：前两步其实就是旋转、平移，通过这两个操作把相机对准目标。（切记先旋转在平移）
   3.把相机坐标移动回原点。
   4.把相机坐标旋转到和原点重叠。
   PS：相机坐标对准目标物后，通过逆向的平移和旋转操作，得到一个复合的矩阵，只要把这个复合的矩阵 乘以 目标坐标，就可以得到相机坐标。下面简单说一下具体计算过程：
   C = T * R
   C（相机camera），T（平移translation），R（旋转rotation），上述步骤前两步就是把相机进行平移旋转操作。
   C^-1 = (T * R)^-1 = R^-1T^-1
   而我们最终需要求得的目标矩阵就是C^-1，只要得到它，就可以乘以目标的世界坐标，获得目标的相机坐标。
   T的逆向矩阵很简单就可以求得：
   
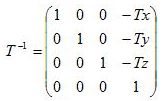
   而R的逆向矩阵就比较难求了，所以我们换个思路通过UVN向量来求R的逆向矩阵。具体UVN的旋转过程大致如：
   [ Ux Uy Uz ]
   [ Vx Vy Vz ]
   [ Nx Ny Nz ]
   所以最终结算结果是：
   

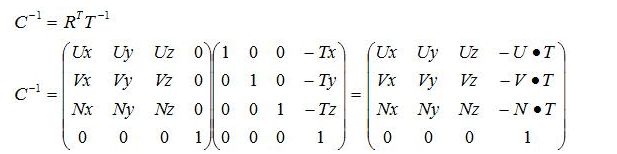
参考资料：https://blog.csdn.net/popy007/article/details/5120158#1792539

五.向量计算
1.向量加法：
U + V = (Ux + Vx, Uy + Vy)

2.向量减法：
U - V = (Ux - Vx, Uy - Vy)

向量加减图示：

3.向量数乘（乘一个常量，如果A为负，则代表反方向）：
A * U = (AUx, AUy)

4.点乘（内积）：
A * B = (Ax * Bx) + (Ay * By) = C
C是一个标量！

A * B = |A| * |B| * cosθ
如果A和B是单位向量，单位向量的模是1，则|A| = |B| = 1, 所以有A * B = cosθ

应用：1.利用点积计算角度； 2.检查两个向量是否正交； 3.计算A向量在B向量的投影长度。
在【unity shader入门精要】中有较为详细清晰的解说。

5.叉乘（外积）：

A * B = |A| * |B| * sinθ
应用：1.获得由向量A和向量B构成的平面的法向量； 2.计算结果的值在二维平面上等于向量A和向量B构成的四边形的面积。
参考阅读：https://www.zhihu.com/question/21080171

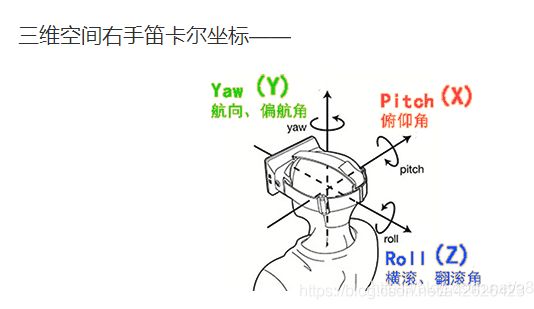
六.pitch、yaw、roll三个角的区别

pitch()：俯仰，将物体绕X轴旋转（localRotationX）
yaw()：航向，将物体绕Y轴旋转（localRotationY）
roll()：横滚，将物体绕Z轴旋转（localRotationZ）

七.矩阵初等变换
1.交换矩阵的两行（列）
2.矩阵的某一行（列）乘以一个非零数
3.矩阵的某一行（列）乘以一个非零数加到另一行（列）
把一个矩阵连接一个单位矩阵，然后通过上面的3条规则，把左边的矩阵变换成单位矩阵，然后右边的矩阵就完成了初等变换了。
矩阵单位化的其中一种方式。

八.光照
1.环境光：
被建模为一个没有光源、没有方向并且对场景中的所有物体产生相同的点亮效果的一种光。
计算过程： 环境光 = 光照颜色 * 光照强度
最终像素点颜色 = 当前像素点颜色（材质颜色） * 环境光

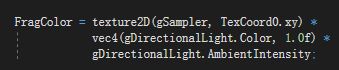
2.漫射光：
与环境光的方向无关性相反，漫射光的方向很重要，因为不是垂直入射的话，漫射光强度会有所衰减，所以我们通过光源向量和法线向量的夹角余弦值计算漫射参数。
漫射光 = 光照颜色 * 漫射强度 * 漫射参数（通过光源向量（单位向量）和法线向量（单位向量）的点积，计算出两向量间夹角余弦值）
漫射参数 = 法向量 *(点乘) 逆光照向量（光照方向的反方向）
法向量的计算方法：因为多个三角形共用一个顶点时，他们的法向量是不同的，所以我们把所有共用三角形顶点的法向量加起来然后再进行单位化得出一个比较合理的法向量。然后通过顶点着色器传递到片段着色器时进行的插值计算，平均每块片元之间的法向量的值。

PS：对一些数值进行计算时，切记能把计算放在C++进行的千万别放在顶点着色器和片段着色器上计算。C++计算可能只算一次或者每次渲染算一次，但放顶点和片元算的次数就多了…… 举个例子，漫射参数计算中， 法向量因为要通过插值传到片段着色器，所以只能在片段着色器进行单位化没办法，但逆光照向量是固定的，他的单位化完全可以在C++中计算完成再传入，无需在片段着色器另行计算。

计算物体同时被环境光和漫射光照时的着色： 最终像素点颜色 = 当前像素点颜色（材质颜色） * （环境光 + 漫射光）

3.镜面反射光：
环境光和漫射光的参数都是和那束光本身关联的，但镜面反射光的参数会根据材质不同（有不同的反射强度）而不同，所以镜面反射光的参数得独立出来，跟材质关联。

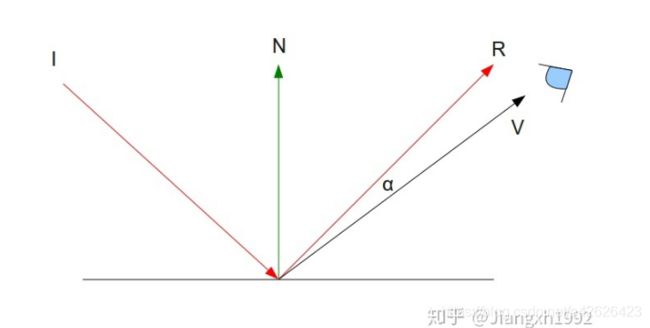
如上图，I为入射光，R为折射后的光，然后我们知道观察者的位置，就可以计算出V。
V = 世界坐标原点到顶点的向量 - 世界坐标原点到观察者位置的向量
得知V和R之后，就可以用类似上面漫射光的计算方式，通过计算α的余弦值算出折射光参数，也是0度时光线最强，超过90度看不到折射光。 要计算α首先得算出向量R。

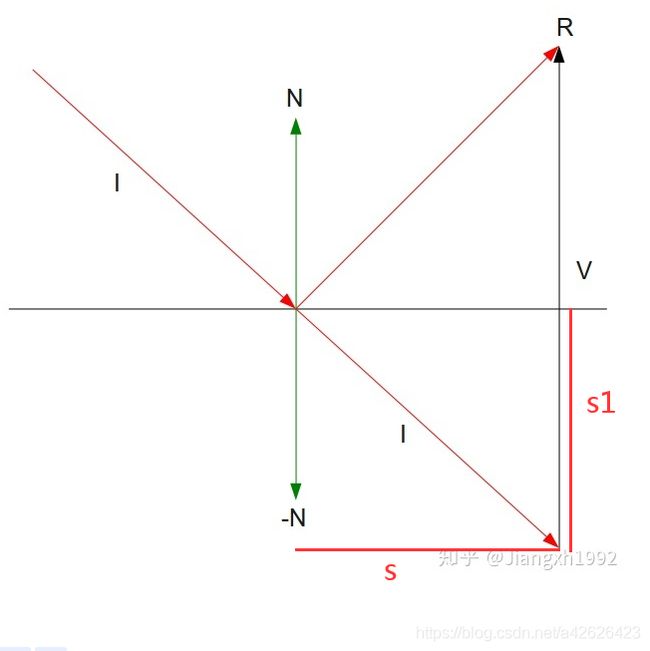
因为向量是没有位置的，只有长度和方向，所以把I平移到下面来。
1.平移I到下面来。
2. -N • I = S。（通过I和-N点乘得出投影长度S）
3. S = S1。 2 * S1 = V的长度
4. 向量V = N * 2 * S1
5.计算出向量V后，通过向量加法，向量R = I + V。 就可以最终计算出向量R出来了。
当然GLSL内置函数reflect已经帮我们完成上面的计算了，只需要传入原始光线向量，物体表面法向量就可以算出R来
R = reflect(I, N)

镜面反射光 = 光照颜色 * （反射参数 的 N(反光度系数，越大亮点越小)次方）
反射参数 = 反射光向量 • 观察点向量

具体计算过程大致如下：

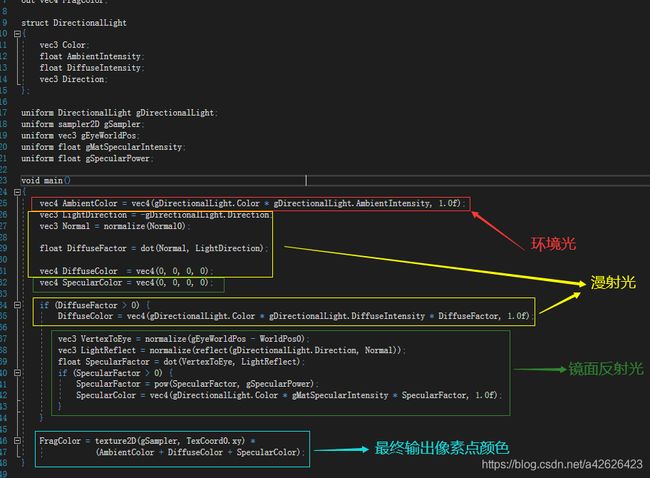
以上3种光（环境光、漫射光、镜面反射光）都是属于平衡光，没有光源起点，所以也不会因为距离增大而衰弱。

4.点光源：
会向各个方向均匀照射，而且会根据距离而渐渐衰减。在数学中，点光源强度公式：
点光源到物体上的强度 = 点光源 / (物体到光源的距离 * 物体到光源的距离)
但由于用这种公式来计算，效果上不那么好看，所以我们修改了一下公式，加入三个衰减的参数因子，让显示出来的点光源更自然真实。
光的强度 = 点光源 / （常量参数1 + 线性参数2 * 物体到光源的距离 + 指数参数3 * (物体到光源的距离 * 物体到光源的距离)）
当常量参数1 = 0， 线性参数2 = 0， 指数参数3 = 1时，此公式就和实际的数学公式一致了。

5.聚光灯：
聚光灯依然维持着很多点光源已有的特性，在此基础上，加上一个方向（灯光照射的方向）和一个阈值（光源方向和光可以照射到的地方的最大夹角），就形成了聚光灯光源了。

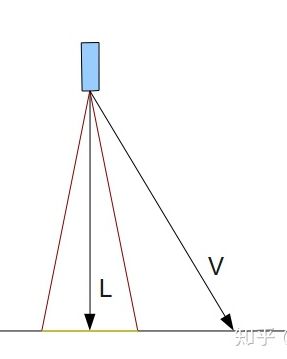
我们只需要计算光源到目标位置的向量V和光源方向L的夹角，比较夹角的余弦值和 L与红色线夹角的余弦值，就可以得出V是在灯照射范围内还是范围外了。

法线：
如果多个面共用同一个顶点，如果设置这个顶点的法线才合适？
1.使用其中一个面的法线作为这个顶点的法线。 （效果无比的差，不需要考虑）
2.计算所有面的法线，然后他们的平均值作为这个顶点的法线（一般情况下用这种方式较为合理，但在某些特殊情况下还是需要注意，如：两个面公用一个顶点，而其中一个面的面积非常大而另外一个面的面积非常小，这时这个顶点的法线就会因为一个面积很小的面而受到很大的影响，导致面积很大的面最终出来的效果不理想）
3.为了解决方案2的问题，在每个面上根据面积之类的再加一个权值，每条法线乘权值再取平均值（计算比较复杂，如非特殊情况还是方案2好）
4.不共用顶点，每个面独立顶点，如果几个面的顶点在同一个位置，就坐标相同法向量不同（这样效果是最好的，但会多出来很多的顶点，对性能有很大的消耗，但随着计算机硬件的提升，慢慢的我们会选择效果更好的方法而不是消耗更少的方法）

法线贴图：
先制作高精细的模型，然后在物体的凹凸表面的每个点上都做法线，通过用RGB颜色通道记录法线的方向，然后生成法线贴图。然后在场景中就可以使用低精度的模型，再贴上法线贴图，就可以实现较真实的效果而使用比较少的资源了。
点评：在刚发现这种方法的时候确实是非常非常实用的东西，但随着硬件性能的逐步提升，以后可能会渐渐的支持直接渲染较高精度的模型了。

公告牌技术：
其实就是一个简单的平面图形，然后他会一直根据镜头的移动而旋转，永远都会把平面对准镜头，让他看起来好像3D物体一样通过不同的角度都能观察到。如果场景有很多怪物，或者一个森林里有很多树木（这种重复度高，数量多的东西），而纹理贴图的形式直接贴在公告版上，然后跟着镜头移动模拟3D效果，就不需要复杂的计算和渲染大量重复的3D模型了。
使用几何着色器，对整个几何图元进行处理，来让公告板时刻对准镜头。

三维拾取：
把用户点击在屏幕上的坐标，对应到三维场景中，看是点中了哪个三维物体。实现思路有两种，基于光栅化和几何算法。
基于光栅化的三维拾取：我们可以在光栅化时把物体的唯一标识渲染到图元上（如：通过颜色缓冲记录相关标识）。这种方法的好处是精准度比较高，坏处是需要渲染两次消耗性能比较大。
先对物体进行一次渲染，把物体的唯一标识标记到颜色缓冲中，然后当需要拾取时（玩家点击屏幕），通过glReadPixels获取玩家点击的像素对应的颜色缓冲数据，就可以把相关唯一标识找出来，然后就可以找到对应的拾取物了。
二次渲染只是把正常物体渲染出来。

基于几何算法的三维拾取：把点击屏幕的坐标利用摄像机的视锥转换为三维射线，然后通过检查场景内哪些物体和射线相交，最早和射线相交的即为拾取对象。这种实现方式比光栅化更为复杂，需要各种计算优化（如：快速排除掉一些根本不可能相交的物体，让后续运算更快）

曲面细分：
当我们观察一个很复杂的模型时，在远处看时使用低精度的显示方式，在近处看时，使用高精度的显示方式。比较简单的实现方式就是使用（LOD技术），生成高精度、平均精度、低精度等多个级别精度的模型，根据距离的不同使用不同精度的模型，但这种做法会大量增加美术资源而且灵活度很低。 OpenGL4.x提供的曲面细分管线允许我们使用较低精度的模型，然后当镜头接近时，把每个三角形细分出更多的小三角形，这就是曲面细分了。

VAO与VBO的前世今生：
openGL可以看着是CS的模式，简单的理解CPU就是Client，GPU就是Server，Client把数据发送到Server端进行处理。
glVertex：
最早期，我们通过glVertex把数据一个个地传输到GPU去处理，每一次渲染都得一个个地把顶点传输到GPU，效率极其低下。
Display List:
把顶点打包成一个list在初始化阶段统一传输给GPU，由GPU来保存数据，这样就不需要在每次执行处理时都一个个顶点发送给GPU了。但还是有他的局限性，如果你需要修改顶点数据，就得把整个list重新发一次给GPU。
Vertex Array：
相对于Display LIst，VA把顶点数据保存于CPU中，每次绘制再把顶点数据打包发送给GPU，这样就相对方便修改。
VBO：
VBO结合了Display List和Vertex Array的优点（绘制时不传输数据，速度快！ 且数据可以打包传输，中途可以修改，灵活）。
VAO：
VAO其实本质上是state-object(状态对象)，是记录了一次绘制所需要的所有信息，包括数据在哪，数据格式等等。我们可以把glEnableVertexAttribArray()-glVertexAttribPointer()等相关命令从绘制阶段放到初始化里面，然后之后简单的绑定一下VAO就可以完成整个绘制了。 VAO虽然不是VBO，但也和VBO强关联，数据始终还是存放在VBO中，VAO只是储存绘制的状态，简化了绘制代码，想绘制哪个，直接绑定VAO就完事了。

减少CPU的开销：
CPU产生的开销主要是调用OpenGL API而产生的驱动开销，这种开销可以分成三类：
1.驱动提交渲染命令的开销，即OpenGL draw函数造成的。
2.驱动提交状态命令导致的状态切换而产生的开销。如：管线中的光照函数切换、片段测试与操作的切换、不同shader,Texture之间的切换、VBO等GPU缓冲对象之间的开销。
3.驱动调用OpenGL API加载或者同步数据的开销。

问题【1】：最简单的就是通过减少draw的次数从而直接减少【1】的开销。如：通过批次合并（用合理的方式把渲染状态相同的多个可渲染物合并到同一个批次进行draw）； 实例渲染（把多个几何数据近似的可渲染物通过一次drawInstance函数绘制，把可渲染物的区别通过数组传入渲染命令中）。
问题【2】：对可渲染物进行有效的排序，尽可能把状态相同的可渲染物依次排在一起，以减少状态切换的次数。

使用非直接绘制技术把需要大量调用draw方式的绘制命令直接存储在GPU上，这样就几乎可以把每次draw都要重复发送给GPU的绘制指令，这种开销降到几乎为0，可以大幅度的减少CPU的开销，如果性能瓶颈不是在GPU而是在CPU这种优化会有好明显的提升。

延迟着色：
前向着色会对每一个物体都执行一个完整的pass（即一次完整的渲染管道流程（VS->TS->GS->光栅化->PS）），但在多光源的情况下，有时要进行多次pass才能完成渲染，而如果场景上出现多个物体遮挡的情况下，被遮挡的部分其实无需进行渲染（反正挡着看不到），所以如果场景有大量遮挡物同时有大量光源时，会做成大量性能浪费在渲染遮挡物上。为了有效的解决这个问题，所以出现了延迟渲染技术。
延迟渲染其实就是在第一次pass的过程中，不进行任何的着色操作，把第一次pass的所有材质相关信息保存到Geometry Buffer（G-Buffer）中。当场景中所有物体都完成了一次pass后，就会形成多组和显示到屏幕上大小一致的数据（法线缓冲、深度缓冲、光滑度缓冲等等）

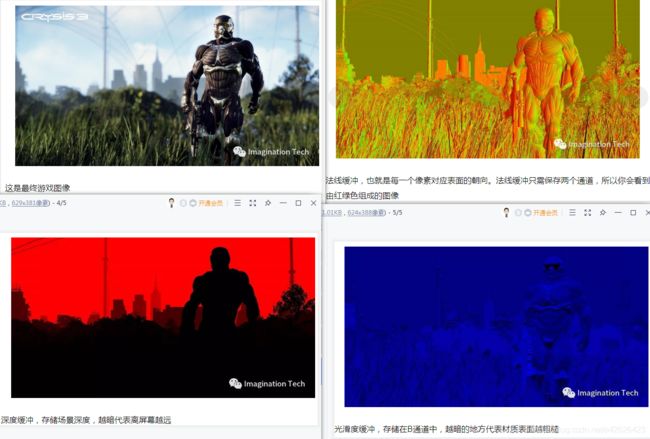
然后在延迟渲染时，只需要取G-Buffer中相关坐标点的数据，结合光照相关公式，就可以计算出最终渲染的结果，而且所有的光照计算都必定是会被现实到屏幕上的，就可以剔除掉前向渲染时，渲染大量被遮挡的，用户看不到的物品。
延迟着色的“延迟”，指的是把整个场景中第一次pass的全部几何信息都缓存下来再一次过着色，虽然保存到G-Buffer的过程中，被遮挡的部分还是会重复计算，但最终进行着色时只需根据G-Buffer的大小一次过渲染就可以了，不会把性能浪费在渲染被遮挡物上。
延迟渲染最重要的作用就是把着色计算和场景复杂度解耦。
优点：
1.光照的开销和场景复杂度无关了。
2.每个像素对光源只会运行一次，就是说不会重复计算被遮挡的像素。

缺点：
1.如果有大量的材质，那么就要需要大量的空间去存储这些G-Buffer，而且在运行的时候也需要较大的数据带宽。
2.对于一些半透明的物体渲染也会有问题，虽然有一些解决方案，但实现下来效率可能也不会比前向渲染高多少。