泊松回归与类泊松回归(《R语言实践(第二版)》)
泊松回归与类泊松回归
- 0. 背景介绍
-
- 0.1 泊松回归:
- 0.2 本示例要做的事:
- 1.导包
- 2.导入数据
- 3.作图
- 4. 拟合泊松回归:
-
- 4.1解释模型参数
- 4.2 检验过度离势(Overdispersion)
- 4.3 对于泊松分布的过度离势
- 4.4泊松分布出现过度离势的主要原因
- 4.5使用gcc包对过度离势进行检验
- 5.类泊松回归
- 参考文献
0. 背景介绍
0.1 泊松回归:
通过一系列连续型和/或类别型预测变量来预测计数型结果变量。
0.2 本示例要做的事:
用癫痫数据(Breslow)讨论在治疗初期的八周内,抗癫痫药物对癫痫发病数的影响。
1.导包
library('robust')#癫痫数据集(Breslow,1993)
library('qcc')#对泊松模型过度离势进行检验
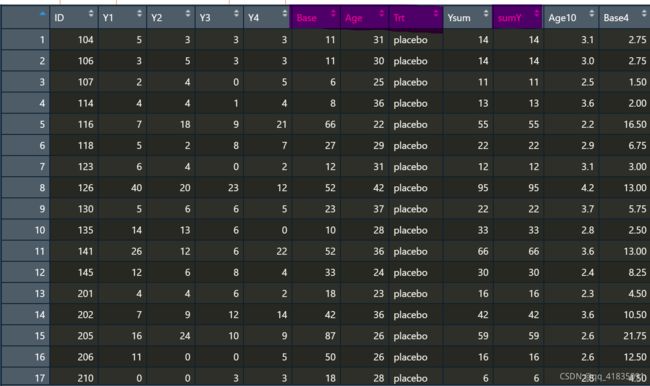
2.导入数据
data(breslow.dat, package="robust")
本数据集中我们只考虑四个变量,其中
因变量是sumY(随机化后八周内癫痫发病数);
自变量为治疗条件(Trt)、年龄(Age)和前八周内的基础癫痫发病数(base).
3.作图
opar <- par(no.readonly=TRUE)
par(mfrow=c(1,2))
attach(breslow.dat)
hist(sumY, breaks=20, xlab="Seizure Count",
main="Distribution of Seizures")
boxplot(sumY ~ Trt, xlab="Treatment", main="Group Comparisons")
par(opar)
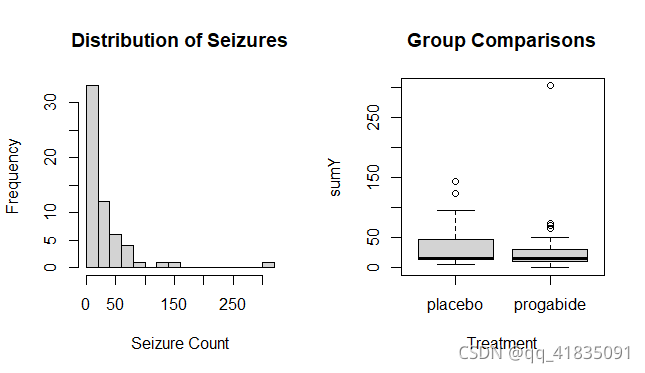
左图是‘Seizures(癫痫)’的分布(x轴为癫痫发生次数,y轴为频率)
右图是‘placebo(安慰剂)’与’progabide(治疗的药物)'的对比
初看图形时,药物治疗下癫痫发病数似乎变小了,且方差也变小了。
4. 拟合泊松回归:
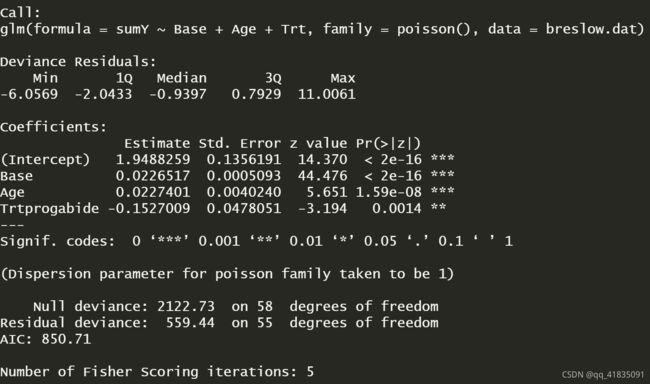
fit <- glm(sumY ~ Base + Age + Trt, data=breslow.dat, family=poisson())
summary(fit)
输出结果列出了偏差、回归参数、标准误和参数为0的检验。注意,此处预测变量在p<0.05的水平下都非常显著。
4.1解释模型参数
coef(fit)
在泊松回归中,因变量以条件均值的对数形式log_e(λ)来建模。年龄的回归参数为0.0227,表明保持其他预测变量不变,年龄增加一岁,癫痫发病数的对数均值将相应增加0.03。截距项即当预测变量都为0时,癫痫发病数的对数均值。由于不可能为0岁,且调查对象的基础癫痫发病数均不为0,因此本例中截距项没有意义。
exp(coef(fit))
在因变量的初始尺度(癫痫发病数,而非发病数的对数)下解释回归系数:
保持其他变量不变,年龄增加一岁,期望的癫痫发病数将乘以1.023。这意 味着年龄的增加与较高的癫痫发病数相关联。更为重要的是,一单位Trt的变化(即从安慰剂到治疗组),期望的癫痫发病数将乘以0.86,也就是说,保持基础癫痫发病数和年龄不变,服药组相对于安慰剂组癫痫发病数降低了20%。
注意:
泊松模型中的指数化参数对响应变量的影响都是成倍增加的,而不是线性相加。
4.2 检验过度离势(Overdispersion)
- 定义:观测到的响应变量的方差大于期望的二项分布的方差。
- 意义:过度离势会导致奇异的标准误检验和不精确的显著性检验。
- 思路:检验φ=残差偏差/残差自由度;若值接近1,则没有过度离势。
4.3 对于泊松分布的过度离势
- 泊松分布的方差和均值相等;
- 处理计数型数据经常发生过度离势。
4.4泊松分布出现过度离势的主要原因
遗漏了某个重要的预测变量。
可能因为事件相关。在泊松分布的观测中,计数中每次事件都被认为是独立发生的。以癫痫数据为例,这意味着对于任何病人,每次癫痫发病的概率与其他癫痫发病的概率相
互独立。但是这个假设通常都无法满足。对于某个病人,在已知他已经发生了39次癫痫
时,第一次发生癫痫的概率不可能与第40次发生癫痫的概率相同。
在纵向数据分析中,重复测量的数据由于内在群聚特性可导致过度离势。此处并不讨论
纵向泊松模型。
deviance(fit)/df.residual(fit)
#deviance:偏差
#df.residual():Returns the residual degrees-of-freedom extracted from a fitted model object.
如果残差偏差与残差自由度的比例远远大于1,那么表明存在过度离势。很明显存在过度离势。
4.5使用gcc包对过度离势进行检验
qcc.overdispersion.test(breslow.dat$sumY, type="poisson")
显著性检验的p值果然小于0.05,进一步表明确实存在过度离势。
函数细节见:qcc.overdispersion.test()
本质是卡方检验D=s2/σ2×(n−1),p<0.05时拒绝原假设.
5.类泊松回归
fit.od <- glm(sumY ~ Base + Age + Trt, data=breslow.dat,
family=quasipoisson())
summary(fit.od)
使用类泊松(quasi-Poisson)方法所得的参数估计与泊松方法相同,但标准误变大了许
多。此处,标准误越大将会导致Trt(和Age)的p值越大于0.05。当考虑过度离势,并控制基础癫痫数和年龄时,并没有充足的证据表明药物治疗相对于使用安慰剂能显著降低癫痫发病次数。
参考文献
《R语言实践(第二版)》