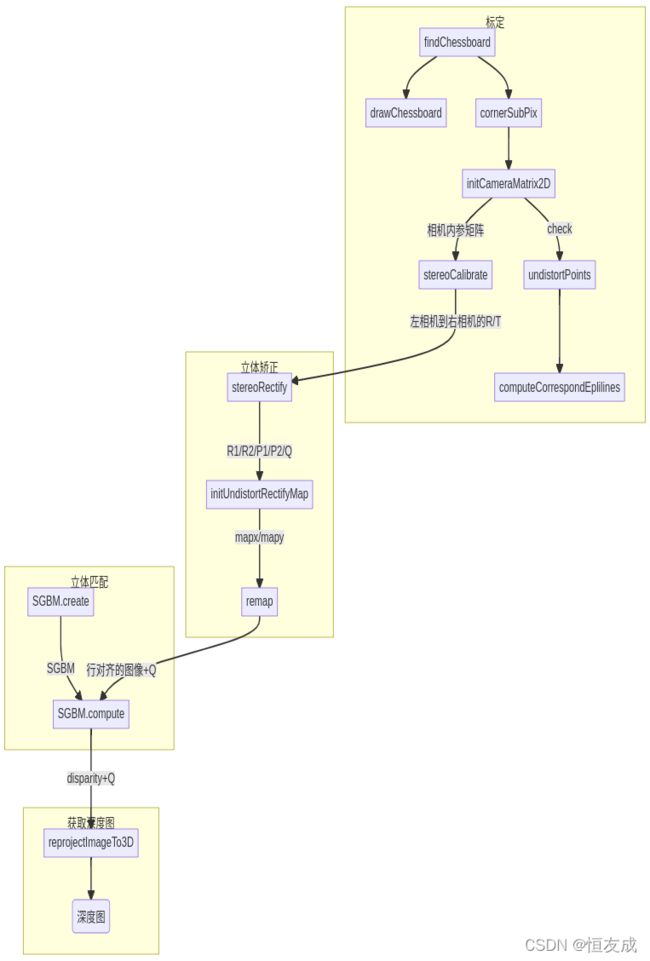
(一) 双目立体视觉介绍
文章目录
- 1 针孔相机模型
- 2.双目相机模型
- 3.立体校正(共面行对准、极线校正)
-
- 3.1极线约束
- 3.2Bouguet算法
- 3.3OpenCV API 介绍
- 4. 立体匹配与视差图
- 5.深度图
-
- 5.1 基础介绍
- 5.2OpenCV API
- 6.双目测距精度分析
- 7.总结
1 针孔相机模型
如基本相机模型及参数中介绍的,首先回忆一下针孔相机模型,
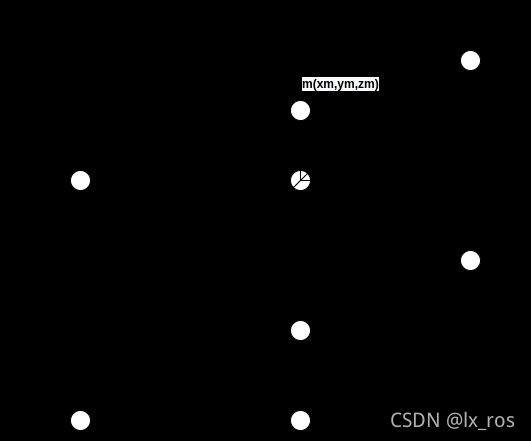
如上图,空间中的一点到图像平面的变换为:
Z M [ x m y m 1 ] = [ f 0 0 0 f 0 0 0 1 ] [ Z M Y M Z M ] Z_M\begin{bmatrix} x_m \\ y_m\\ 1 \end{bmatrix} = \begin{bmatrix} f & 0 & 0\\ 0 & f& 0\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} Z_M \\ Y_M\\ Z_M\end{bmatrix} ZM⎣⎡xmym1⎦⎤=⎣⎡f000f0001⎦⎤⎣⎡ZMYMZM⎦⎤,而图像平面到像素平面的关系可表示为:
[ μ v 1 ] = [ d x 0 μ 0 0 d y v 0 0 0 1 ] [ x m y m 1 ] \begin{bmatrix} \mu\\ v\\ 1 \end{bmatrix}=\begin{bmatrix} d_x & 0 &\mu_0 \\ 0 & d_y& v_0\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_m\\ y_m\\ 1 \end{bmatrix} ⎣⎡μv1⎦⎤=⎣⎡dx000dy0μ0v01⎦⎤⎣⎡xmym1⎦⎤
由以上可知相机坐标系下空间中的点到像素坐标系的变换关系为,
Z M [ μ v 1 ] = [ f d x 0 μ 0 0 f d y v 0 0 0 1 ] [ X M Y M Z M ] = K [ X M Y M Z M ] Z_M\begin{bmatrix} \mu\\ v\\ 1 \end{bmatrix}=\begin{bmatrix} fd_x & 0&\mu_0 \\ 0& fd_y& v_0\\ 0& 0 &1 \end{bmatrix}\begin{bmatrix} X_M\\ Y_M\\ Z_M \end{bmatrix}=K\begin{bmatrix} X_M\\ Y_M\\ Z_M \end{bmatrix} ZM⎣⎡μv1⎦⎤=⎣⎡fdx000fdy0μ0v01⎦⎤⎣⎡XMYMZM⎦⎤=K⎣⎡XMYMZM⎦⎤
K即相机的内参矩阵。
考虑畸变,常用的畸变模型有五个参数,分别是 ( k 1 , k 2 , p 1 , p 2 , k 3 ) (k_1,k_2,p_1,p_2,k_3) (k1,k2,p1,p2,k3)
{ x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) \begin{cases} x_{distorted} = x(1+k_1r^2+k_2r^4+k_3r^6)\\ y_{distorted} = y(1+k_1r^2+k_2r^4+k_3r^6) \end{cases} {xdistorted=x(1+k1r2+k2r4+k3r6)ydistorted=y(1+k1r2+k2r4+k3r6)
( x , y ) (x,y) (x,y)是校正后的像素点, ( x d i s t o r t e d , y d i s t o r t e d ) (x_distorted,y_distorted) (xdistorted,ydistorted)是原图上的像素点, r = x 2 + y 2 r=\sqrt{x^2+y^2} r=x2+y2是像素点到图像中心的距离。
其中 p 1 , p 2 p_1,p_2 p1,p2表示的是切向畸变,是由于安装时导致的镜头不平行镜头平面而产生的安装误差,其描述公式为:
{ x d i s t o r t e d = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y + 2 p 2 x y + p 1 ( r 2 + 2 y 2 ) \begin{cases} x_{distorted} = x + 2p_1xy + p_2(r^2+2x^2) \\ y_{distorted} = y + 2p_2xy + p_1(r^2+2y^2) \end{cases} {xdistorted=x+2p1xy+p2(r2+2x2)ydistorted=y+2p2xy+p1(r2+2y2)
2.双目相机模型
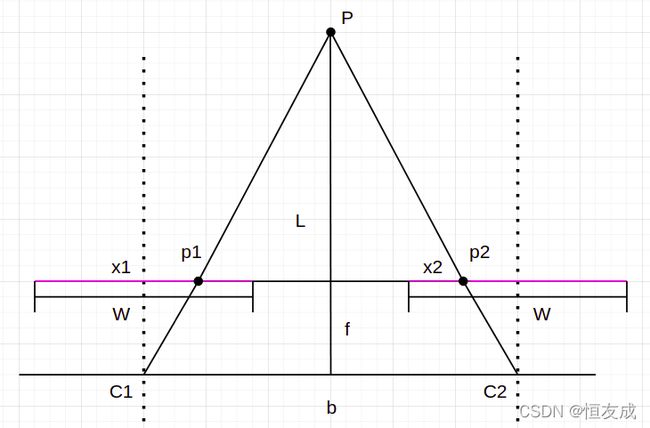
上图所示是最理想的双目相机模型,图中, C 1 , C 2 C_1,C_2 C1,C2分别表示的左右相机的坐标系原点,空间中一点 P P P在左右相机的图像平面中的点如图 p 1 p_1 p1和 p 2 p_2 p2所示,相机 C 1 C_1 C1和 C 2 C_2 C2焦距相同的都为 f f f且两相机在同一平面上,图像平面在同一平面上,两个相机成像的图像像素宽度都为 W W W,则 p 1 p1 p1在左图中横轴上的像素坐标为 x 1 x_1 x1, p 2 p_2 p2在右图中的横轴上的像素坐标为 x 2 x_2 x2,两个相机之间的距离为 b b b,点 P P P到相机平面的距离即深度为 L L L,像平面到相机平面的距离为 f f f。
上图中 △ P p 1 p 2 ∼ △ P C 1 C 2 \triangle Pp_1p_2\sim\triangle PC_1C_2 △Pp1p2∼△PC1C2,因此有如下关系:
b − ( x 1 − W / 2 ) − ( W / 2 − x 2 ) b = L − f L \frac{b-(x_1-W/2) - (W/2-x_2)}{b}=\frac{L-f}{L} bb−(x1−W/2)−(W/2−x2)=LL−f由上式可以求得 L = f b x 1 − x 2 L=\frac{fb}{x_1-x_2} L=x1−x2fb,其中 x 1 − x 2 x_1-x_2 x1−x2表示的是点P在左右相机中的像素点的横坐标之差,也被称为视差。如何在左右图像中匹配到点P的像素点 p 1 p_1 p1、 p 2 p_2 p2是双目测距中的关键,由上述公式可以看出,深度与视差成反比关系,距离越远视差越小,距离越近,视差越小。
实际的双目相机往往无法满足上述理想的条件,这里提出几个问题,
- 如何找到两个图像中相同的像素点的位置?
- 两个相机不在同个平面
- 两个相机的焦距不同怎么样
- 两个相机的图像有多少的是重合的
- 当点距离相机过近时,盲区如何计算
- 两个相机的基线是如何求出来的
- 两个相机获取图像如何同步
3.立体校正(共面行对准、极线校正)
3.1极线约束
1.2中假设两个相机的像平面和基线都是平行的,但实际情况往往并非如此,因此需要将两个视图进行投影变换,使两个成像平面平行于基线,且同一个点在左右两幅图像中位于同一行,以应用上图介绍的三角原理,简称共面行对准。
![]()
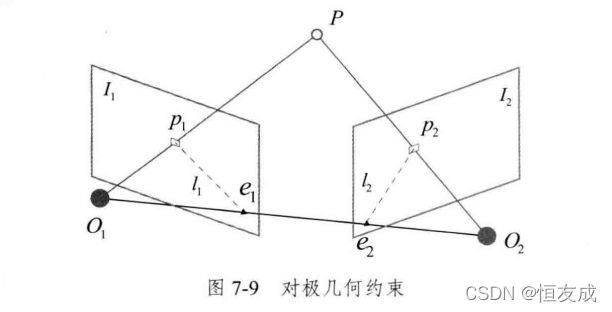
根据对极几何的原理,如下图所示,
点P是空间中的一点, O 1 O_1 O1和 O 2 O_2 O2分别是左右相机的中心,平面 P O 1 O 2 PO_1O_2 PO1O2称为极平面(epipolar plane), O 1 , O 2 O_1,O_2 O1,O2连线与像平面 I 1 , I 2 I_1,I_2 I1,I2的交点分别为 e 1 e_1 e1和 e 2 e_2 e2称为极点(epipoles),如前所述 O 1 O 2 O_1O_2 O1O2称为基线,极平面与图像平面 I 1 , I 2 I_1,I_2 I1,I2的交线称为极线,极线约束是指给定图像上一点,其在另一幅图像上的匹配点一定在对应的极线上。
可以通过对极约束来求左右相机之间的旋转和平移关系。上图中 P ( X , Y , Z ) P(X,Y,Z) P(X,Y,Z)左右相机的两个像素点 p 1 , p 2 p_1,p_2 p1,p2的像素位置由相机的成像原理可知为:
s 1 p 1 = K P 和 s 2 p 2 = K ( R P + t ) s_1p_1=KP和s_2p_2=K(RP+t) s1p1=KP和s2p2=K(RP+t)
这里P的坐标是在左相机的相机坐标系下, R R R和 t t t分别表示左相机坐标系到右相机坐标系下的旋转和平移向量,K是相机的内参矩阵。当使用齐次坐标系(即增加1维为1),一个向量表示为 ( x , y , z , 1 ) T (x,y,z,1)^T (x,y,z,1)T,对其乘以任意的常数后,依然为其自身(需保持最后一维为1)。因此如 s 1 p 1 s_1p_1 s1p1与 p 1 p_1 p1在齐次坐标系下意义相同。这种相等关系为尺度意义下相等,表示为 s p ≃ p sp\simeq p sp≃p,则:
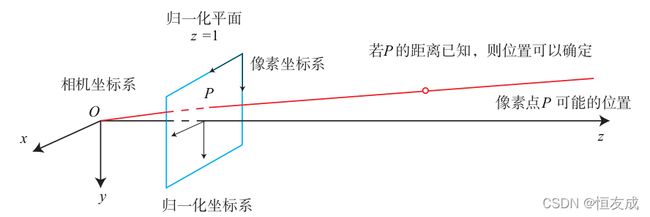
p 1 ≃ K P , p 2 ≃ K ( R P + t ) x 1 = K − 1 p 1 , x 2 = K − 1 p 2 p_1 \simeq KP,p_2 \simeq K(RP+t)\\x_1=K^{-1}p_1,x_2=K^{-1}p_2 p1≃KP,p2≃K(RP+t)x1=K−1p1,x2=K−1p2
这里 x 1 , x 2 x_1,x_2 x1,x2表示归一化平面上的坐标,归一化平面的表示如下图:
代入上式,
x 2 ≃ R x 1 + t x_2\simeq Rx_1+t x2≃Rx1+t
两边同时左乘向量 t t t的反对称矩阵 t ∧ t^{\wedge} t∧,相当于与向量 t t t做外积
t ∧ x 2 ≃ t ∧ R x 1 t^{\wedge} x_2\simeq t^{\wedge}Rx_1 t∧x2≃t∧Rx1
两侧同时左乘 x 2 T x_2^T x2T得:
x 2 T t ∧ x 2 ≃ x 2 T t ∧ R x 1 x_2^Tt^\wedge x_2\simeq x_2^Tt^\wedge Rx_1 x2Tt∧x2≃x2Tt∧Rx1
上式中由向量的外积和内积的性质可知,左侧恒为零,因此上式可写为:
x 2 T t ∧ R x 1 = 0 x_2^Tt^\wedge Rx_1 = 0 x2Tt∧Rx1=0
重新代入 p 1 , p 2 p_1,p_2 p1,p2可以得到:
p 2 T K − T t ∧ R K − 1 p 1 = 0 p_2^TK^{-T}t^\wedge RK^{-1}p_1=0 p2TK−Tt∧RK−1p1=0
这个公式称为对极约束,它的几何意义是 O 1 , O 2 , P O_1,O_2,P O1,O2,P三点共面。把上式中间部分记作两个矩阵,基础矩阵(Fundamental Matrix)和本质矩阵(Essential Matrix),上式可简化为:
E = t ∧ R , F = K − T E K − 1 , x 2 T E x 1 = p 2 T F p 1 = 0 E=t^\wedge R, F=K^{-T}EK^{-1},x_2^TEx_1=p_2^TFp_1=0 E=t∧R,F=K−TEK−1,x2TEx1=p2TFp1=0
因此求处矩阵E或F就能求出R和t,就能求出左右相机之间的关系,就能求出相机的基线长度。
我们做立体校正的目的,正是为了得到如双目相机模型中描述的那样,使两条极线共线,以进行高效的立体匹配,因此立体匹配也称为极线校正,立体校正所做的事情就是根据摄像头定标后获得的单目内参数据(焦距、成像原点、畸变系数)和双目相对位置关系(旋转矩阵和平移向量),分别对左右视图进行消除畸变和行对准,使得左右视图的成像原点坐标一致、两摄像头光轴平行、左右成像平面共面、对极线行对齐。
3.2Bouguet算法
以Bouguet算法为例说明立体校正的过程。
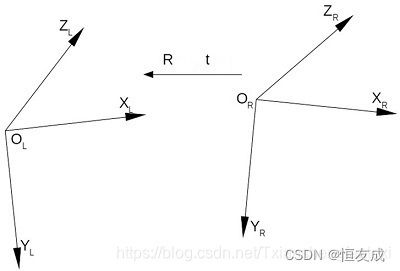
假设右目到左目的旋转矩阵和平移矩阵分别为R和T,如下图:
引用自:
https://blog.csdn.net/Txianshengfantexi/article/details/119454616
空间中的点 P P P在左右相机坐标系的坐标的关系为:
P l = R P r + T P_l = RP_r+T Pl=RPr+T
Bouguet双目立体校正,
-
首先
- 左相机坐标系沿旋转向量R的正方向旋转一半的R(向量),记该旋转为 R h 1 R_{h1} Rh1;
- 右相机坐标系沿旋转向量R的反方向旋转一半的R(向量),记该旋转为 R h 2 R_{h2} Rh2
- 如下图所示:[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-q4diPmox-1647592312229)(imgs/2_h12.jpg)]
结果为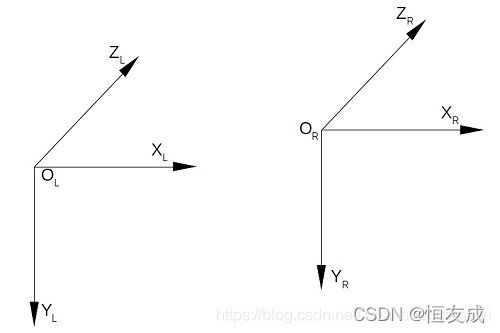
经过左右相机一半的旋转后,左相机坐标系和右相机坐标系平行但不共面,此时,左右相机的x轴、y轴和z轴分别平行,但是左右相机的xoy平面不共面,满足关系 P l = P r + R h 2 ∗ T P_l=P_r+R_{h2}*T Pl=Pr+Rh2∗T记 t = R h 2 ∗ T t = R_{h2}*T t=Rh2∗T
-
然后,将平行但不共面的左右相机坐标系旋转 R r e c t R_{rect} Rrect至与矫正坐标系 O r e c t − X r e c t Y r e c t Z r e c t O_{rect}-X_{rect} Y_{rect} Z_{rect} Orect−XrectYrectZrect平行,使左右相机坐标系平行且共面:
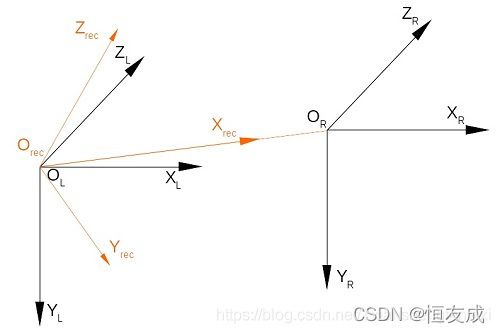
矫正后满足:
- 矫正坐标系的 O r e c t X r e c t O_{rect}X_{rect} OrectXrect 轴 与 左右相机坐标系 原点连线 O L O R O_LO_R OLOR 平行,其正方向由 O L O_L OL指向 O R O_R OR;
- 矫正坐标系的 X r e c t O r e c t Z r e c t X_{rect}O_{rect}Z_{rect} XrectOrectZrect平面与平面 Z L O L O R Z R Z_LO_LO_RZ_R ZLOLORZR 平行,矫正坐标系的 O r e c t Y r e c t O_{rect}Y_{rect} OrectYrect轴垂直该平面。
- 矫正矩阵 R r e c t R_{rect} Rrect 的每一列分别对应相机坐标系基轴(单位向量)在矫正坐标系中的投影;而矫正矩阵 R r e c t R_{rect} Rrect的每一行分别对应矫正坐标系基轴(单位向量)在相机坐标系中的投影。
- 旋转矩阵 R r e c t R_{rect} Rrect的构造方法构是通过右相机相对于左相机的偏移矩阵T完成的,使得基线与成像平面平行,推导参考6。
- 最终得到左右相机的旋转矩阵为:
{ R l = R r e c t ∗ R h 1 R r = R r e c t ∗ R h 2 \left\{\begin{matrix} R_l = R_{rect}*R_{h1}\\ R_r = R_{rect}*R_{h2} \end{matrix}\right. {Rl=Rrect∗Rh1Rr=Rrect∗Rh2这正是OpenCV函数StereoRectify函数返回的 R 1 R_1 R1和 R 2 R_2 R2
得到左右相机的旋转矩阵之后,即可进行立体校正,步骤:
- 分别将两个图像的像素坐标系通过共同的内参矩阵转换到相机坐标系;
- 分别对两个相机坐标系进行旋转得到新的相机坐标系,通过左乘旋转矩阵 R l R_l Rl逆和 R r R_r Rr逆;(极线约束)
- 针对新的相机坐标分别进行左、右相机的去畸变操作;
- 去畸变操作结束后,分别用左、右相机的内参矩阵将左、右两个相机坐标系重新转换到左、右图像像素坐标系;
- 并分别用左、右源图像的像素值对新左、右图像的像素点进行插值
3.3OpenCV API 介绍
stereoRectify DOC
void cv::stereoRectify (
InputArray cameraMatrix1,
InputArray distCoeffs1,
InputArray cameraMatrix2,
InputArray distCoeffs2,
Size imageSize,
InputArray R,
InputArray T,
OutputArray R1,
OutputArray R2,
OutputArray P1,
OutputArray P2,
OutputArray Q,
int flags = CALIB_ZERO_DISPARITY,
double alpha = -1,
Size newImageSize = Size(),
Rect* validPixROI1 = 0,
Rect* validPixROI2 = 0
)
- R R R第一个相机坐标系到第二个相机坐标系下的旋转矩阵
- T T T第一个相机坐标到第二个相机坐标下的平移向量
- R 1 R_1 R1 第一个相机的修正变换 3 × 3 3\times 3 3×3矩阵,将第一个相机坐标系中的点变换到第一个相机对应的修正坐标系下
- P 1 P_1 P1第一个相机在第一个相机的修正坐标系下的 3 × 4 3\times 4 3×4投影矩阵。将第一个相机修正坐标系下的点投影到第一个相机修正图像上
- Q Q Q, 4 × 4 4\times 4 4×4的视差到深度的映射矩阵,结合
reprojectImageTo3D函数,将视差图转为深度图。 - f l a g s flags flags,值为0或
CALIB_ZERO_DISPARITY,如果设置此参数,则每个相机的主点在修正后的图像中是不变的。
R R R、 T T T可通过 stereoCalibrate函数获得。对于水平双目,左右目相机在修正后的相机中主要是X轴方向的偏移,相应的左右目的极线是水平的,y轴相同, P 1 P_1 P1和 P 2 P_2 P2形如:
P1 = [ f 0 c x 1 0 0 f c y 0 0 0 1 0 ] P2 = [ f 0 c x 2 T x ∗ f 0 f c y 0 0 0 1 0 ] \texttt{P1} = \begin{bmatrix} f & 0 & cx_1 & 0 \\ 0 & f & cy & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \\ \texttt{P2} = \begin{bmatrix} f & 0 & cx_2 & T_x*f \\ 0 & f & cy & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} P1=⎣⎡f000f0cx1cy1000⎦⎤P2=⎣⎡f000f0cx2cy1Tx∗f00⎦⎤
其中 T x T_x Tx是两个相机的水平偏移。另外,如果设置 flags=CALIB_ZERO_DISPARITY,则 c x 1 = = c x 2 cx_1==cx_2 cx1==cx2。可见 P 1 P_1 P1, P 2 P_2 P2等效于修正后的相机的参数矩阵,因此 P 1 P_1 P1、 P 2 P_2 P2、 R 1 R_1 R1、 R 2 R_2 R2可以作为 initUndistortRectifyMap函数的参数,得到左右目到修正后的图像坐标系下的映射。
4. 立体匹配与视差图
结合前述双目相机模型的介绍可知,双目深度的估计依赖于视差图的计算,为了计算视差,需要找到左右图像上相同的像素点,这正是立体匹配要做的事。
引用自https://blog.csdn.net/guyuealian/article/details/121301896#t9
大部分立体匹配算法的计算过程可以分成以下几个阶段:匹配代价计算、代价聚合、视差优化、视差细化。立体匹配是立体视觉中一个很难的部分,主要困难在于:
- 1)图像中可能存在重复纹理和弱纹理,这些区域很难匹配正确;
- 2)由于左右相机的拍摄位置不同,图像中几乎必然存在遮挡区域,在遮挡区域,左图中有一些像素点在右图中并没有对应的点,反之亦然;
- 3)左右相机所接收的光照情况不同;
- 4)过度曝光区域难以匹配;
- 5)倾斜表面、弯曲表面、非朗伯体表面;
- 6)图像噪声等。
常用的立体匹配方法基本上可以分为两类:局部方法,例如BM、SGM、ELAS、Patch Match等,非局部的,即全局方法,例如Dynamic Programming、Graph Cut、Belief Propagation等,局部方法计算量小,匹配质量相对较低,全局方法省略了代价聚合而采用了优化能量函数的方法,匹配质量较高,但是计算量也比较大。
目前OpenCV中已经实现的方法有BM、binaryBM、SGBM、binarySGBM、BM(cuda)、Bellief Propogation(cuda)、Constant Space Bellief Propogation(cuda)这几种方法。比较好用的是SGBM算法,
在立体匹配生成视差图之后,还可以对视差图进行滤波后处理,例如Guided Filter、Fast Global Smooth Filter(一种快速WLS滤波方法)、Bilatera Filter、TDSR、RBS等。 视差图滤波能够将稀疏视差转变为稠密视差,并在一定程度上降低视差图噪声,改善视差图的视觉效果,但是比较依赖初始视差图的质量。
以 OpenCV中实现的 StereoSGBM算法为例:
cv::Ptr<cv::StereoSGBM> sgbm = cv::StereoSGBM::create(
0, 96, 9, 8*9*9, 32*9*9, 1, 63, 10, 100, 32
);
sgbm->compute(left, right, disparity) // 使用的是立体校正的图像
5.深度图
5.1 基础介绍
得到视差图后,需将其转换为深度图,由2.双目相机模型中的介绍可知,深度 L = f b x 1 − x 2 L=\frac{fb}{x_1-x_2} L=x1−x2fb,其中 x 1 − x 2 x_1-x_2 x1−x2表示的是点P(X,Y,Z)在左右相机中的像素点的横坐标之差,即视差。L即点P在空间中的Z轴坐标,由
[ μ v 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X Z Y Z 1 ] \begin{bmatrix} \mu \\ v\\ 1 \end{bmatrix}=\begin{bmatrix} f_x &0 &cx \\ 0 & f_y & cy\\ 0 & 0 &1 \end{bmatrix}\begin{bmatrix} \frac{X}{Z}\\ \frac{Y}{Z}\\ 1 \end{bmatrix} ⎣⎡μv1⎦⎤=⎣⎡fx000fy0cxcy1⎦⎤⎣⎡ZXZY1⎦⎤可得:
{ X = Z ( μ − c x ) f x Y = Z ( μ − c y ) f y Z = L \left\{\begin{matrix} X=\frac{Z(\mu-c_x) }{f_x}\\ Y=\frac{Z(\mu-c_y) }{f_y}\\ Z=L \end{matrix}\right. ⎩⎪⎨⎪⎧X=fxZ(μ−cx)Y=fyZ(μ−cy)Z=L
代码示例:
vector<Eigen::Vector4d, Eigen::aligned_allocator<Eigen::Vector4d>> points;
for(int v=0; v<left.rows; v++)
for(int u=0; u<left.cols; u++) {
if(disparity.at<float>(v,u) <= 0.0 || disparity.at<float>(v,u) >= 96.0) continue;
Eigen::Vector4d point(0, 0, 0, left.at<uchar>(v,u)/255.);
double x = (u - cx) / fx;
double y = (v - cy) / fy;
double d = fx * b / (disparity.at<float>(v, u));
point[0] = x * d;
point[1] = y * d;
point[2] = d;
points.push_back(point);
}
5.2OpenCV API
视差图转深度图在 OpenCV中可用reprojectImageTo3D函数来实现
void cv::reprojectImageTo3D (
InputArray disparity,
OutputArray _3dImage,
InputArray Q,
bool handleMissingValues = false,
int ddepth = -1
)
disparity是前述立体匹配得到的视差图_3dImage函数的输出,是size同输入disparity的3通道浮点型矩阵,_3dImage[i][j]表示第i行第j列的点的空间坐标 ( x , y , z ) (x,y,z) (x,y,z),若函数的输入Q矩阵是通过stereoRectify函数计算得来的,那么坐标 ( x , y , z ) (x,y,z) (x,y,z)是相对于第一个相机的修正坐标系的。Q是 4 × 4 4\times 4 4×4的透视变换矩阵,可通过stereoRectify函数获得。
6.双目测距精度分析
https://blog.csdn.net/xuyuhua1985/article/details/50151269
根据深度 L = f b x 1 − x 2 L=\frac{fb}{x_1-x_2} L=x1−x2fb可以看出,某点像素的深度精度取决于该点处估计的视差d的精度。假设视差d的误差恒定,当测量距离越远,得到的深度精度则越差,因此使用双目相机不适宜测量太远的目标。
如果想要对与较远的目标能够得到较为可靠的深度,一方面需要提高相机的基线距离,但是基线距离越大,左右视图的重叠区域就会变小,内容差异变大,从而提高立体匹配的难度,另一方面可以选择更大焦距的相机,然而焦距越大,相机的视域则越小,导致离相机较近的物体的距离难以估计。
理论上,深度方向的测量误差与测量距离的平方成正比,而X/Y方向的误差与距离成正比;而距离很近时,由于存在死角,会导致难以匹配的问题;想象一下,如果你眼前放置一块物体,那你左眼只能看到物体左侧表面,右眼同理只能看到物体右侧表面,这时由于配准失败,导致视差计算失败;这个问题在基线越长,问题就越严重
7.总结
REFERENCE
1.https://blog.csdn.net/lx_ros/article/details/121000802
2.https://aijishu.com/a/1060000000139727
3.https://blog.csdn.net/qq_42722197/article/details/118663803
4.https://blog.csdn.net/guyuealian/article/details/121301896#t9
5.https://www.cnblogs.com/zyly/p/9373991.html
6.https://blog.csdn.net/Txianshengfantexi/article/details/119454616