基于Pytorch的自编码(AutoEncoder)学习
基于Pytorch的自编码(AutoEncoder)学习
-
- 前言
- 一、什么是自编码(What is AutoEnconder)?
-
- 1. Encoder
- 2. Decoder
- 二、autoEnconder 源码
- 三、编码效果对比
欢迎学习交流!
邮箱: z…@1…6.com
网站: https://zephyrhours.github.io/
前言
笔者在学习深度学习过程中,首先针对AutoEncoder进行了简单的学习,虽然网上有很多相关资料,但是绝大多部分写的很粗,尤其是包含代码和详细介绍的少之又少。不过笔者发现一篇博文写的非常不错,非常适合新手学习和了解自编码,博客后面会附生原文链接,感兴趣的朋友可以看一下!
一、什么是自编码(What is AutoEnconder)?
自编码器( Autoencoder) 最原始的概念很简单,简单来说就是将一组数据输入神经网络中,然后经过神经网络训练后,得到的输出数据跟输入数据一模一样。整个自编码器( Autoencoder) 可以拆解成 编码器 (Encoder) 和 解码器(Decoder) 两个神经网络。编码器 吃进的原始数据 在经过神经网络后,原始数据就会被压缩成一个维度较小的向量Z,这部分就是编码的整个过程;然后将向量Z输入解码器中,将向量Z还原成原始数据大小。虽然听起来很容易,但是具体的实施过程确是相对有点复杂,需要具有一定的数学功底,具体过程可以通过下面的这个图来简单说明。
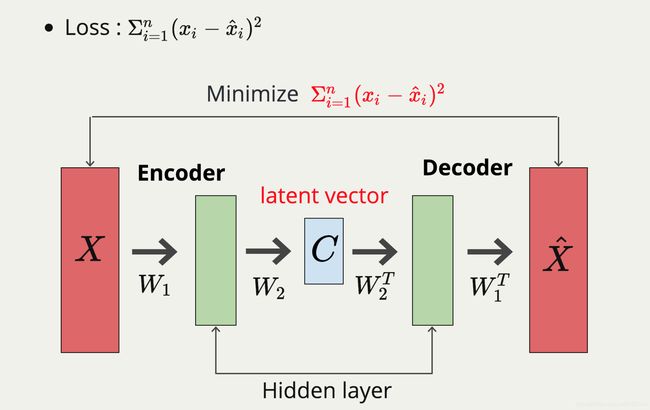
1. Encoder
为了方便初学者了解,下面笔者以上图为例子,进行简单的说明。其实整个编码的过程就是负责将原始数据X进行输入,然后根据网络模型对其进行压缩,将原始高维度的数据X压缩成低维度数据C,而这些低维度数据(也就是上面图中的C)通常习惯上被称为隐层空间数据 (latent vector),原始数据经过非线性隐含层(Hidden layer)的激活函数操作后,原始数据就会被转换到一个低维度空间,这个空间被认为是高级特征空间。这里有点类似PCA对高维度数据压缩的感觉,可以理解为编码就是将原始数据转换到特征空间。但是不同之处在于Enconder是非线性的降维变换,这点不同于PCA变换。
2. Decoder
解码就是将原始隐含层数据转换回原始数据空间,是一个将低维度数据像高维度数据转换的过程,跟PCA变换的后一段,利用特征向量与特征值对数据进行投影重构的过程。但是不同之处在于PCA变化改变了高维度数据的初始维度,而经过自编码后得到的数据是与原始数据的维度是相同的。
对于衡量自编码的工作状态就需要用到损失函数来对其进行评估,具体这里不再赘述。下面直接放上具体的自编码代码和具体实验结果,给初学者参考。
二、autoEnconder 源码
下面是基于MNIST数据编写的一个简单自编码(autoEnconder)代码,初学者可以配置好相应环境后,直接拿去使用。有点需要提的是,强烈建议windows 用户使用anaconda来安装,因为这个anaconda除了内置了一些必要的库环境外,还可以根据用户需求进行环境虚拟,这样就可以根据不同的项目需求单独设置相应环境,免去了重新安装、各种bug的烦恼。编辑器建议使用Pycharm,笔者认为这是一个非常优秀的编辑器,当然还有许多不错的编辑器,用户根据自己的需求自行挑选就可以。笔者使用的开发环境具体如下:
版本要求:
- Python 3.7
- Pytorch 1.8.1
具体代码:
# Author: Zephyr Hou
# Time: 2021-08-16
import os
import torch
import torchvision
from torch import nn
from torch.autograd import Variable
from torch.utils.data import DataLoader
from torchvision import transforms
from torchvision.datasets import MNIST
from torchvision.utils import save_image
if not os.path.exists('./mlp_img'):
os.mkdir('./mlp_img')
# Parameter Setting
num_epochs = 100
batch_size = 128
learning_rate = 1e-3
def to_img(x):
x = 0.5 * (x + 1)
x = x.clamp(0, 1)
x = x.view(x.size(0), 1, 28, 28)
return x
img_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5])
])
# Mnist digits dataset
train_data = torchvision.datasets.MNIST(
root='./data/mnist/',
train=True,
transform=torchvision.transforms.ToTensor(), # converts a PIL.Image or numpy.ndarry to torch.FloatTensor(C x H x W)
download=True,
)
dataLoader = DataLoader(train_data, batch_size=batch_size, shuffle=True)
class autoEncoder(nn.Module):
def __init__(self):
super(autoEncoder, self).__init__()
self.encoder = nn.Sequential(
nn.Linear(28 * 28, 128),
nn.ReLU(True),
nn.Linear(128, 64),
nn.ReLU(True), nn.Linear(64, 12), nn.ReLU(True), nn.Linear(12, 3))
self.decoder = nn.Sequential(
nn.Linear(3, 12),
nn.ReLU(True),
nn.Linear(12, 64),
nn.ReLU(True),
nn.Linear(64, 128),
nn.ReLU(True), nn.Linear(128, 28 * 28), nn.Tanh())
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
return x
model = autoEncoder().cuda() # autoEncoder model
loss_func = nn.MSELoss() # loss function
optimizer = torch.optim.Adam(
model.parameters(), lr=learning_rate, weight_decay=1e-5)
for epoch in range(num_epochs):
for data in dataLoader:
img, _ = data
img = img.view(img.size(0), -1)
img = Variable(img).cuda()
# ===================forward=====================
output = model(img)
loss = loss_func(output, img)
# ===================backward====================
optimizer.zero_grad()
loss.backward()
optimizer.step()
# ===================log========================
print('epoch [{}/{}], loss:{:.4f}'.format(epoch + 1, num_epochs, loss.item()))
if epoch % 10 == 0:
pic = to_img(output.cpu().data)
save_image(pic, './mlp_img/image_{}.png'.format(epoch))
pic1 = to_img(img.data)
save_image(pic1, './mlp_img/Ori_image_{}.png'.format(epoch))
三、编码效果对比
下面我们来看一下具体的效果,如下图所示,第一行的三张图是从MNIST数据中随机筛选的三组数据,第二行三张图是利用上述自编码分别学习1次,10次和20次后的效果展示。从下面数据可以看出,经过的训练次数越多,最后生成的图像与真实的图像越相似。这里单纯从效果来看,对于二维图像自编码有点类似滤波操作的效果,但是本质上是完全不同的,这点要加以区分。
参考文献:
- https://blog.csdn.net/xyk_hust/article/details/87630809
- https://medium.com/ai-academy-taiwan/what-are-autoencoders-175b474d74d1