机器学习基础补习01---微积分与概率论基础
玩了将近一个月的我终于又回来继续学习啦~~~,最近开始补习一些机器学习中需要的数学知识,就把个人学习过程记录在csdn博客吧。
1.什么是机器学习?
Tom Michael Mitchell在他的非常经典的书《machine learning》中给出的定义如下:
对于某给定的任务T,在合理的性能度量方案P的前提下,某计算机程序可以自主学习任务T的经验E,随着提供合适的、优质的、大量的经验E,该程序对于任务T的性能逐步提高。
这里比较重要的机器学习的对象是:
(1)任务Task T,一个或者多个
(2)经验Experience E
(3)性能Performance P
即随着任务的不断执行,经验的累积会带来计算机性能的提升。
换个表述:
机器学习是人工智能的一个分支。我们使用计算机设计一个系统,使它能够根据提供的训练数据按照一定的方式来学习;随着训练次数的增加,该系统可以在性能上不断学习和改进,通过优化该学习模型,能够基于先前学习得到的参数来预测相关问题的输出。
当然了,很难具体说清楚到底什么是机器学习,还是要自己慢慢理解。
思考一下,机器如何发现新词?(没有词库和词典的情况下)
中文的几个汉字经常出现在一起的话,那这就可能是一个新词,所以我们需要考虑以下几个因素:
(1)频数:Count(X)
(2)凝固程度
a. X =A B
b. P(A)P(B) vs P(X)
如果A和B是独立的话,那我们就不认为它们组合在一起是一个新词,也就是凝固程度很差
如果P(A)P(B)和P(X)经常很接近的话,那我们会倾向于A和B会组成一个新词
(3)自由度
a. aXb
b. 信息熵H(a)、H(b)
信息熵在以后的文章中会详加解释
(4)凝固程度和自由程度缺一不可,只考虑凝固程度,会找出“巧克”,“俄罗”,“五颜六”、“柴可夫”等“半个词”;只考虑自由程度,会把“吃了一顿”、“看了一遍”、“睡了一晚”,“去了一趟”中的“了一”提取出来,因为它的左右邻字都太丰富了。
那么来思考一个问题,给定一个长文本,如何利用上述参数来设计一个可行算法?
也许可以用双数组Trie树来解决这个问题
这是一个简单的例子,可以看到发现一个新词对于机器来说也很不容易。
2.ok,现在来进入正式的学习内容
(1)回忆知识
求S的值:
S = 1 0 ! + 1 1 ! + 1 2 ! + 1 3 ! + 1 4 ! + . . . + 1 n ! + . . . S=\frac 1{0!}+\frac 1{1!}+\frac 1{2!}+\frac 1{3!}+\frac 1{4!}+...+\frac 1{n!}+... S=0!1+1!1+2!1+3!1+4!1+...+n!1+...
复习微积分:夹逼定理
当x∈U( x 0 x_0 x0,r)时,有g(x)≤f(x)≤h(x)成立,并且 lim x → x 0 g ( x ) = A \lim_{x \to \ x_0}g(x)=A x→ x0limg(x)=A, lim x → x 0 h ( x ) = A \lim_{x \to \ x_0}h(x)=A x→ x0limh(x)=A那么则有: lim x → x 0 f ( x ) = A \lim_{x \to \ x_0}f(x)=A x→ x0limf(x)=A
g(x)和h(x)都没有特殊限制,只要求当x相同时,g(x)和h(x)的极限相等。
来看一下它的应用:

如上图所示,我们可以看到sinx
从而: lim x → 0 s i n x x = 1 \lim_{x \to \ 0}\frac {sinx}{x}=1 x→ 0limxsinx=1(非常基础的一个极限公式)
该极限式将三角函数和多项式建立了极限关系
复习微积分:极限存在定理
单调有界数列必有极限,如:单增数列有上界,则其必有极限
构造一个数列{ x n x_n xn}
x n = ( 1 + 1 n ) m x_n=(1+\frac1n)^m xn=(1+n1)m直接把该数列展开,我们得到:
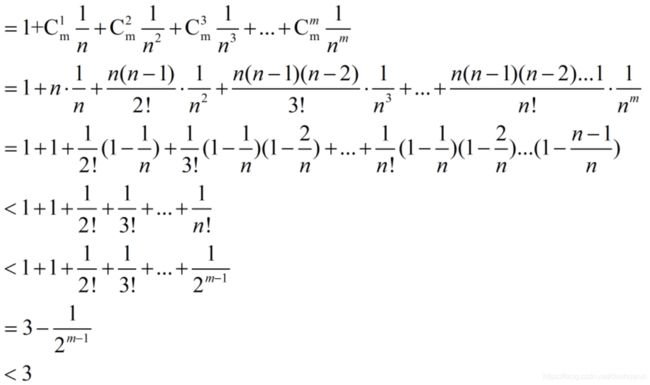
所以说该数组是有上界的,且上界为3
自然常数
根据前文中 a n = ( 1 + 1 n ) a_n=(1+\frac1n) an=(1+n1)的二项展开式,已经证明数组{ a n a_n an}单增有上界,因此,必有极限,记作e
同时:有以下式子成立:
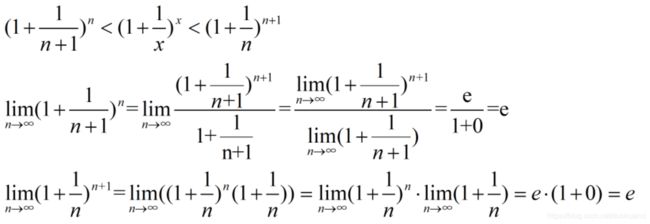
根据夹逼定理,函数 f ( x ) = ( 1 + 1 x ) x f(x)=(1+\frac1x)^x f(x)=(1+x1)x的极限存在,为e
目前e的具体值还不清楚,只知道它比3要小。
导数
(1)简单的说,导数就是曲线的斜率,是曲线变化快慢的反应
(2)二阶导数是斜率变化快慢的反应,表征曲线的凹凸性
a. 在GIS中,往往一条二阶导数连续的曲线,我们称之为“光顺“的
b. 加速度的方向总是指向轨迹曲线凹的一侧
应用;
(1)已知函数 f ( x ) = x x , x > 0 f(x)=x^x,x>0 f(x)=xx,x>0
(2)求f(x)的最小值
a. 领会幂指函数的一般处理套路
b. 在信息熵章节中将再次遇到它
求解:
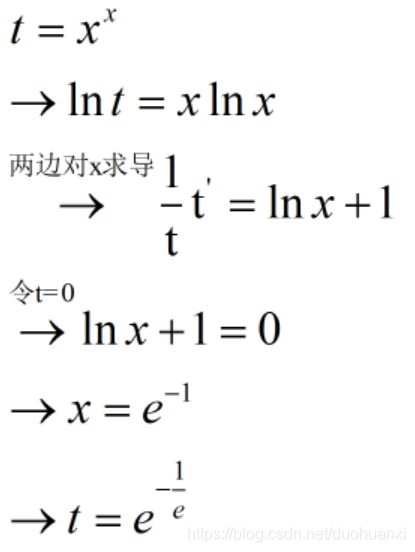
所以求幂指函数时,先求对数再求导
泰勒展开式
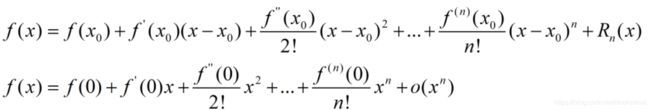
泰勒公式的应用1
数值计算:初等函数值的计算(在原点展开)

在实践中,往往需要做一定程度的变换。
计算 e x : e^x: ex:
(1)给定正实数x,计算 e x = ? e^x=? ex=?
(2)一种可行的思路:
a. 求整数k和小数r,使得:
x = k ∗ l n 2 + r , ∣ r ∣ < = 0.5 ∗ l n 2 x=k*ln2+r,|r|<=0.5*ln2 x=k∗ln2+r,∣r∣<=0.5∗ln2
b.从而:
e x = e k ⋅ l n 2 + r = e k ⋅ l n 2 ⋅ e r = 2 k ⋅ e r e^x=e^{k\cdot ln2+r}=e^{k\cdot ln2}\cdot e^r=2^k \cdot e^r ex=ek⋅ln2+r=ek⋅ln2⋅er=2k⋅er
方向导数
如果函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点P(x,y)是可微分的,那么,函数在该点沿任一方向L的方向导数都存在,且有:
∂ f ∂ l = ∂ f ∂ x c o s ψ + ∂ f ∂ y s i n ψ \frac{\partial f}{\partial l}=\frac{\partial f}{\partial x}cos\psi+\frac{\partial f}{\partial y}sin\psi ∂l∂f=∂x∂fcosψ+∂y∂fsinψ
其中: ψ \psi ψ为x轴到方向L的转角
梯度
(1)设函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在平面区域D内具有一阶连续偏导数,则对于每一个点P(x,y)∈D,向量: ( ∂ f ∂ x , ∂ f ∂ y ) (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}) (∂x∂f,∂y∂f)为函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点P的梯度,记作grad f(x,y)
(2)梯度的方向是函数在该点变化最快的方向
a.考虑一座解析式为 z = H ( x , y ) z=H(x,y) z=H(x,y)的山,在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的梯度是在该点梯度变化最快的方向
(3)梯度下降法:思考:若下山方向和梯度呈 θ \theta θ夹角,下降速度是多少?(考虑方向导数)
凸函数
若函数f的定义域domf为凸集,且满足:
∀ x , y ∈ d o m f , 0 ≤ θ ≤ 1 \forall x,y∈domf,0≤\theta≤1 ∀x,y∈domf,0≤θ≤1,有:
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f(\theta x+(1-\theta)y)≤\theta f(x)+(1-\theta)f(y) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
凸函数的判定:
(1)定理:f(x)在区间[a,b]上连续,在(a,b)内二阶可导,那么:
a. 若 f ′ ′ ( x ) > 0 f^{''}(x)>0 f′′(x)>0,则f(x)是凸的
b. 若 f ′ ′ ( x ) < 0 f^{''}(x)<0 f′′(x)<0,则f(x)是凹的
即:一元二阶可微的函数在区间上是凸的,当且仅当它的二阶导数是非负的
凸性质的应用
(1)设p(x),q(x)是在X中取值的两个概率分布,给定如下定义式:
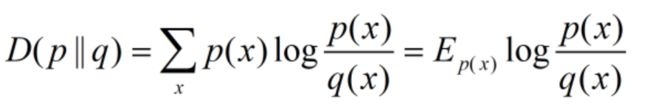
试证明:D(p||q)≥0
上式在最大熵模型等内容中会详细讨论
可以在以下图像中看出y=-logx在定义域上是凸函数
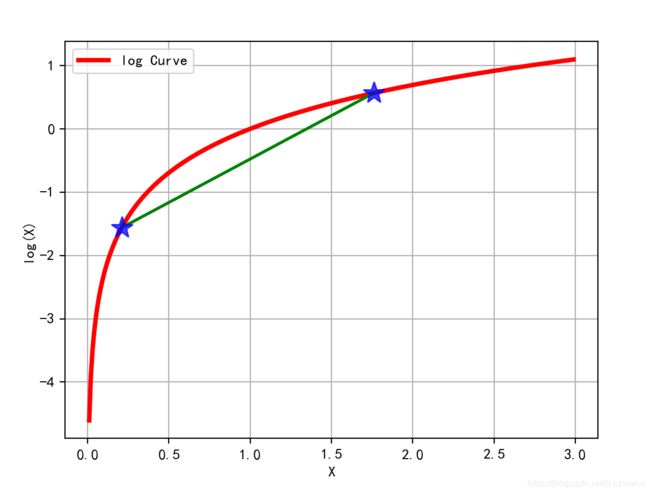
![]()
概率论
(1)对概率的认识:P(x)∈[0,1]
a. P=0:事件出现的概率为0—>事件不会发生?
b. 若x为离散/连续变量,则P( x = x 0 x=x_0 x=x0)表示 x 0 x_0 x0发生的概率/概率密度
(2)累计分布函数: Φ ( x ) = P ( x ≤ x 0 ) \Phi(x)=P(x≤x_0) Φ(x)=P(x≤x0)
a. Φ ( x ) \Phi(x) Φ(x)一定为单增函数
b. m i n ( Φ ( x ) ) = 0 , m a x ( Φ ( x ) ) = 1 min(\Phi(x))=0,max(\Phi (x))=1 min(Φ(x))=0,max(Φ(x))=1
c. 将值域为[0,1]的某函数 y = f ( x ) y=f(x) y=f(x)看成y事件的累积概率
d. 若 y = f ( x ) y=f(x) y=f(x)可导,则 p ( x ) = f ( x ) p(x)=f(x) p(x)=f(x)为某概率密度函数
古典概型
举例:将n个不同的球放入N(N≥n)个盒子中,假设盒子容量无限,求事件A={每个盒子至多有1个球}的概率
解: P ( A ) = P N n N n P(A)=\frac{P^n _N}{N^n} P(A)=NnPNn
(1)基本事件总数:
a.第1个球,有N种放法;
b.第2个球,有N中放法;
…
d.共: N n N^n Nn种放法
(2)每个盒子至多放1个球的事件数:
a.第1个球,有N种放法;
b.第2个球,有N-1种放法;
c.第3个球,有N-2种放法;
…
d.共: N ( N − 1 ) ( N − 2 ) . . . ( N − n + 1 ) = P N n N(N-1)(N-2)...(N-n+1)=P^n_N N(N−1)(N−2)...(N−n+1)=PNn
装箱问题:
将12件正品和3件次品随机装在3个箱子中,每箱装5件,每箱中恰有1件次品的概率是多少?
解:(1)将15件产品装入3个箱子,每箱装5件,共有 15 ! 5 ! 5 ! 5 ! \frac{15!}{5!5!5!} 5!5!5!15!种装法
(2)先把3件次品放入3个箱子,有3!种装法。对于这样的每一种装法,把其余12件产品装入3个箱子,每箱装4件,共有 12 ! 4 ! 4 ! 4 ! \frac{12!}{4!4!4!} 4!4!4!12!种装法
(3) P ( A ) = ( 3 ! ∗ 12 ! ) ( 4 ! 4 ! 4 ! ) ( 15 ! ) ( 5 ! 5 ! 5 ! ) P(A)=\frac{\frac{(3!*12!)}{(4!4!4!)}}{\frac{(15!)}{(5!5!5!)}} P(A)=(5!5!5!)(15!)(4!4!4!)(3!∗12!)= 25 91 \frac{25}{91} 9125
与组合数的关系
(1)把n个物品分成k组,使得每组物品的个数分别为n1,n2…nk,(n=n1+n2+…+nk),则不同的分组方法有 n ! n 1 ! n 2 ! n 3 ! . . . n k ! \frac{n!}{n_1!n_2!n_3!...n_k!} n1!n2!n3!...nk!n!种。
(2)上述问题的简化版本,即n个物品分成2组,第一组m个,第二组n-m个,则分组方法有: n ! m ! ( n − 1 ) ! \frac{n!}{m!(n-1)!} m!(n−1)!n!,即: C n m C^m_n Cnm
商品推荐
(1)商品推荐场景中过于聚焦的商品推荐往往会损害用户的购物体验,在有些场景中,系统会通过一定程度的随机性给用户带来发现的惊喜感。
(2)假设在某推荐场景中,经计算A和B两个商品与当前访问用户的匹配度分别为0.8和0.2,系统将随机为A生成一个均匀分布于0到0.8的最终得分,为B生成一个均匀分布于0到0.2的最终得分,试计算最终B的分数大于A的分数的概率
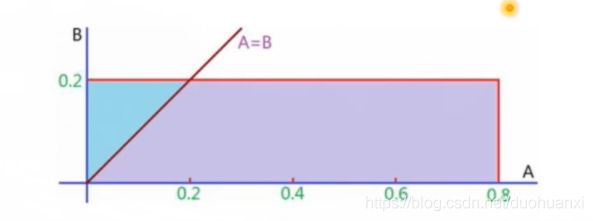
解:如上图所示,A=B的直线上方区域即为B>A的情况。
S 蓝 色 = 0.02 , S 矩 形 = 0.16 S_{蓝色}=0.02,S_{矩形}=0.16 S蓝色=0.02,S矩形=0.16
p = 0.02 0.16 = 0.125 p=\frac{0.02}{0.16}=0.125 p=0.160.02=0.125
概率公式
(1)条件概率: P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B)=\frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)
(2)全概率公式: P ( A ) = ∑ P ( A ∣ B i ) P ( B i ) P(A)=\sum P(A|B_i)P(B_i) P(A)=∑P(A∣Bi)P(Bi)
(3)贝叶斯(Bayes)公式:
P ( B i ∣ A ) = P ( A ∣ B i ) P ( B i ) ∑ P ( A ∣ B j ) P ( B j ) P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum P(A|B_j)P(B_j)} P(Bi∣A)=∑P(A∣Bj)P(Bj)P(A∣Bi)P(Bi)
贝叶斯公式的应用
(1)8支步枪中有5支已校准过,3支未校准,一名射手用校准过的枪射击,中靶概率为0.8;用未校准过的枪设计,中靶概率为0.3;现从8支枪中随机取一支设计,结果中靶,求该枪是已校准过的概率。
解:
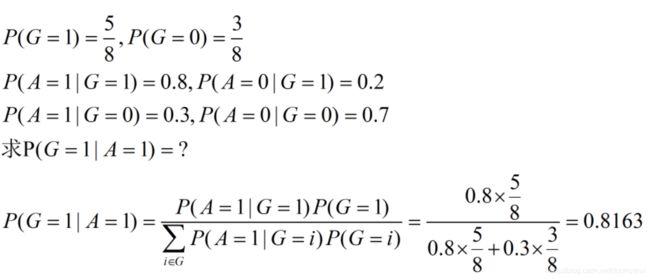
贝叶斯公式 P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
(1)给定某系统的若干样本x,计算该系统的参数,即:
P ( θ ∣ x ) = P ( x ∣ θ ) P ( θ ) P ( x ) P(\theta|x)=\frac{P(x|\theta)P(\theta)}{P(x)} P(θ∣x)=P(x)P(x∣θ)P(θ)
a.P( θ \theta θ):没有数据支持下, θ \theta θ发生的概率:先验概率
b.P(\theta|x):在数据x的支持下, θ \theta θ发生的概率:后验概率
c.P(x| θ \theta θ):给定某参数 θ \theta θ的概率分布:似然函数
两点分布
0-1分布
已知随机变量X的分布律为:

则有:E(X)=p
D (X)=p(1-p)
二项分布
设随机变量X服从参数为n,p的二项分布,设 X i X_i Xi为第i次试验中事件A发生的次数,i=1,2…n,则:
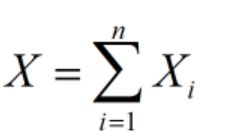
显然, X i X_i Xi相互独立均服从参数为p的0-1分布,所以:
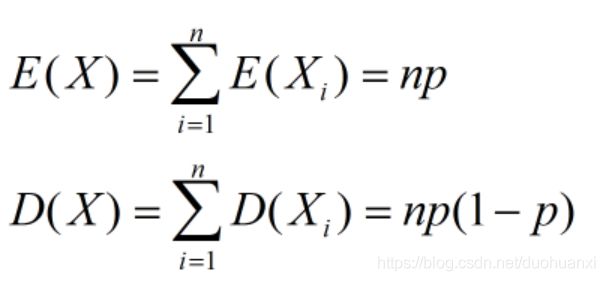
泊松分布
设X~π( λ \lambda λ),且分布律为: P ( X = k ) = λ k k ! e − λ P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda} P(X=k)=k!λke−λ,k=0,1,2,…, λ > 0 \lambda>0 λ>0
则有: E ( X ) = λ E(X)=\lambda E(X)=λ, D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 = λ 2 + λ − λ 2 = λ D(X)=E(X^2)-[E(X)]^2=\lambda^2+\lambda-\lambda^2=\lambda D(X)=E(X2)−[E(X)]2=λ2+λ−λ2=λ
所以泊松分布的期望和方差都等于参数 λ \lambda λ
在实际事例中,当一个随机事件,以固定的平均瞬时速率 λ \lambda λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P( λ \lambda λ)
如:a.某一服务设施在一定时间内到达的人数
b.电话交换机接到呼叫的次数 c.汽车站台的侯客人数 d. 机器出现的故障数
均匀分布
设X~U(a,b),其概率密度为:
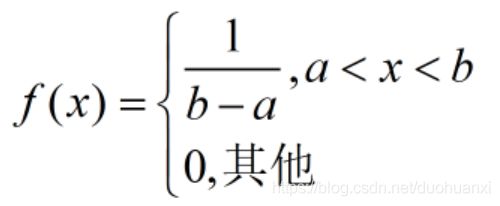
则有 E ( X ) = ∫ − ∞ ∞ x f ( x ) d x = ∫ a b 1 b − a x d x = 1 2 ( a + b ) E(X)=\int_{-\infty}^{\infty}xf(x)dx=\int_a^b\frac{1}{b-a}xdx=\frac{1}{2}(a+b) E(X)=∫−∞∞xf(x)dx=∫abb−a1xdx=21(a+b)
D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 = ∫ a b x 2 1 b − a d x − ( a + b 2 ) 2 = ( b − a ) 2 12 D(X)=E(X^2)-[E(X)]^2=\int_a^bx^2\frac{1}{b-a}dx-(\frac{a+b}{2})^2=\frac{(b-a)^2}{12} D(X)=E(X2)−[E(X)]2=∫abx2b−a1dx−(2a+b)2=12(b−a)2
指数分布
设随机变量X服从指数分布,其概率密度为:
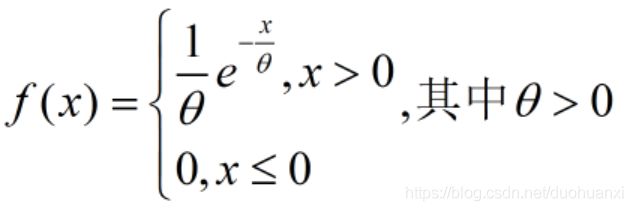
则有E(X)= θ \theta θ
D(X)= θ 2 \theta^2 θ2
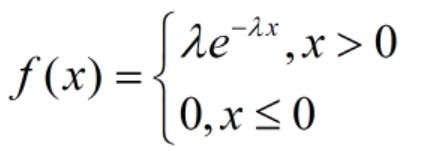
其中, λ > 0 \lambda>0 λ>0是分布的一个参数,常被称为概率参数。即:每单位时间内发生某事件的次数。指数分布的区间是 [ 0 , ∞ ) [0,\infty) [0,∞)。
指数分布可以用来表述独立随机事件发生的时间间隔,比如旅客进机场的时间间隔,软件更新的时间间隔等等。
许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可以用指数分布来近似,它在可靠性研究中是最常用的一种分布形式。
指数分布的一个重要特性是无记忆性
如果一个随机变量呈指数分布,当s,t≥0时,有:
P ( x > s + t ∣ x > s ) = P ( x > t ) P(x>s+t|x>s)=P(x>t) P(x>s+t∣x>s)=P(x>t)
即,如果x是某一元件的寿命,已知元件使用了s小时,它总共使用至少s+t小时的条件概率,与从开始使用时算起它使用至少t小时的概率相等。
正态分布
设X~N( μ , σ 2 \mu,\sigma^2 μ,σ2),其概率密度为:
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 , σ > 0 , − ∞ < x < ∞ f(x)=\frac{1}{\sqrt{2π}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\sigma>0,-\infty
则有: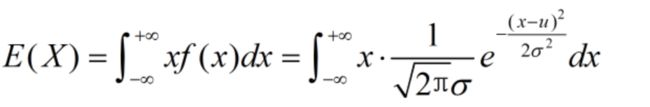
令 x − μ σ = t = > x = μ + σ t \frac{x-\mu}{\sigma}=t=>x=\mu+\sigma t σx−μ=t=>x=μ+σt,
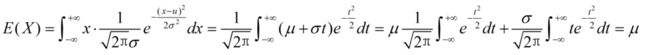
D(X)= σ 2 \sigma^2 σ2
集合Hash问题
某Hash函数将任一字符串非均匀映射到正整数k,概率为 2 − k 2^{-k} 2−k,如下所示,现有字符串集合S,某元素经映射后,得到的最大整数为10,试估计S的元素个数。
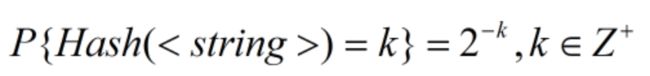
问题分析:(1)由于Hash映射成整数是指数级衰减的,“最大整数为10”这一条件可近似考虑成“整数10曾经出现”,继续近似成“整数10出现过一次”,字符串被映射成10的概率为 p = 2 − 10 = 1 1024 p=2^{-10}=\frac{1}{1024} p=2−10=10241,从而,一次映射即两点分布:
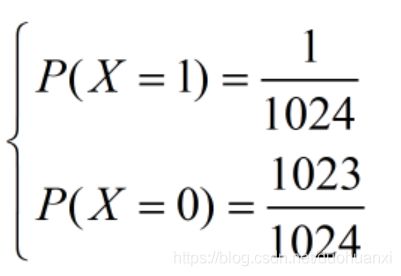
这篇文章写得有些乱,主要是一些基本知识的复习