Sklearn——PCA主成分分析

1.特征降维

降维实际上就是把高维空间的数据转换映射到低维空间中，从而达到降低数据维度的目的，降维前后特征的数量是不变的。

2.特征选择和特征降维的区别

1.特征选择：特征选择其实是一个“丢弃不重要的属性特征”的过程，对数据特征的重要程度进行排序，在按照要求直接“丢弃”相应数量的特征列，以达到减小运算规模的效果，特征选择后保留下的列的数据值是不变的，和特征选择前相同。
2.特征降维：降维实际上是一种空间的转换，即把高位空间数据映射到低维空间去，相当于进行了坐标变换，数据点本身是不动的，相应地，降维后数据点的坐标值会发生变化。

3.常用降维算法

PCA降维：即主成分分析，也是最常用的一种降维算法，其思想就是寻找一个空间，使得各样本点到投影坐标轴上的距离（误差）最小。
T-SNE：西瓜书中介绍的流形学习方法就是这种降维算法的主要思想，即在低维空间中找出高维数据的流形映射，可以使用降维+聚类的迭代来实现算法。
LDA：也叫线性判别式分析，LDA是监督式的将为，需要传入数据的结果标签，主要思想就是设法把样本投影到这样一条直线上：同类样本在直线上的距离最近，不同类样本在直线上的距离最远。
FA：即因子分析，因子分析其实就是认为高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的，由此思想来进行降维。
此外，还有一些降维算法（如SVD矩阵奇异值分解，实际上在sklearn的PCA算法中就用到了奇异值分解）

4.sklearn中PCA算法函数

1.主成分分析 (PCA)

# 添加目录到系统路径方便导入模块
import sys
from pathlib import Path
curr_path = str(Path().absolute())
parent_path = str(Path().absolute().parent)
p_parent_path = str(Path().absolute().parent.parent)
sys.path.append(p_parent_path)
print(f"主目录为：{p_parent_path}")

from torch.utils.data import DataLoader
from torchvision import datasets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np

from sklearn.decomposition import PCA

train_dataset = datasets.MNIST(root = p_parent_path+'/datasets/', train = True,transform = transforms.ToTensor(), download = False)
test_dataset = datasets.MNIST(root = p_parent_path+'/datasets/', train = False, 
                               transform = transforms.ToTensor(), download = False)
batch_size = len(train_dataset)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=True)
X_train,y_train = next(iter(train_loader))
X_test,y_test = next(iter(test_loader))
X_train,y_train = X_train.cpu().numpy(),y_train.cpu().numpy() # tensor转为array形式)
X_test,y_test = X_test.cpu().numpy(),y_test.cpu().numpy() # tensor转为array形式)
X_train = X_train.reshape(X_train.shape[0],784)
X_test = X_test.reshape(X_test.shape[0],784)
m, p = X_train.shape # m：训练集数量，p：特征维度数
print(f"原本特征维度数：{p}") # 特征维度数为784

# n_components是>=1的整数时，表示期望PCA降维后的特征维度数
# n_components是[0,1]的数时，表示主成分的方差和所占的最小比例阈值，PCA类自己去根据样本特征方差来决定降维到的维度
model = PCA(n_components = 0.95)
lower_dimensional_data = model.fit_transform(X_train)
print(f"降维后的特征维度数：{model.n_components_}")

approximation = model.inverse_transform(lower_dimensional_data)  # 降维后的数据还原
plt.figure(figsize=(8,4))

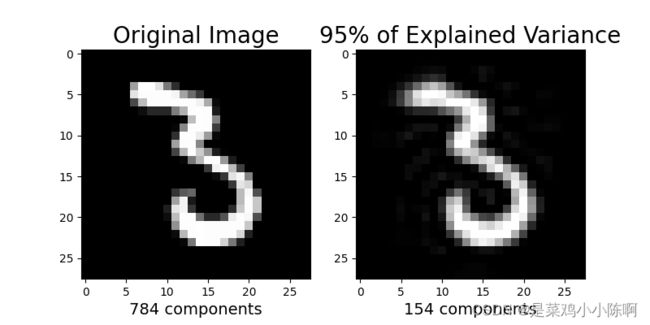
#原始图片
plt.subplot(1,2,1)
plt.imshow(X_train[1].reshape(28,28),
        cmap = plt.cm.gray, interpolation='nearest',
        clim=(0,1))
plt.xlabel(f'{X_train.shape[1]} components', fontsize = 14)
plt.title('Original Image', fontsize = 20)
#降维后的图片
plt.subplot(1,2,2)
plt.imshow(approximation[1].reshape(28,28),
            cmap = plt.cm.gray, interpolation='nearest',
            clim = (0,1))
plt.xlabel(f'{model.n_components_} components', fontsize = 14)
plt.title('95% of Explained Variance', fontsize = 20)
plt.show()

2.不同主成分个数对应的可解释方差分析(Explained Variance)

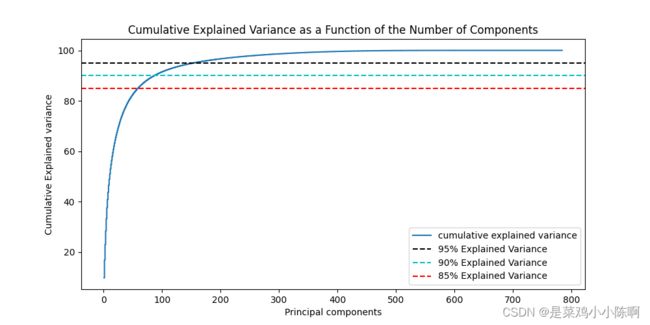
model = PCA()# 这里需要分析所有主成分，所以不降维
model.fit(X_train)
tot = sum(model.explained_variance_) #方差分析
var_exp = [(i/tot)*100 for i in sorted(model.explained_variance_,reverse=True)]
cum_var_exp = np.cumsum(var_exp)
plt.figure(figsize=(10,5))
plt.step(range(1, p+1), cum_var_exp, where='mid',label='cumulative explained variance') # p：特征维度数
plt.title('Cumulative Explained Variance as a Function of the Number of Components')
plt.ylabel('Cumulative Explained variance')
plt.xlabel('Principal components')
plt.axhline(y = 95, color='k', linestyle='--', label = '95% Explained Variance')
plt.axhline(y = 90, color='c', linestyle='--', label = '90% Explained Variance')
plt.axhline(y = 85, color='r', linestyle='--', label = '85% Explained Variance')
plt.legend(loc='best')
plt.show()

def explained_variance(percentage, images):
    '''
    parm: percentage[float]:降维的百分比
    return:approx_original:降维后还原的图片
    return:model.n_components_:降维后的主成分个数
    '''
    model = PCA(percentage)
    model.fit(images)
    components = model.transform(images)
    approx_original= model.inverse_transform(components)
    return approx_original,model.n_components_
plt.figure(figsize=(8,10))
percentages = [784,0.99,0.95,0.90]
for i in range(1,5):
    plt.subplot(2,2,i)
    im, n_components =  explained_variance(percentages[i-1], X_train)
    im = im[5].reshape(28,28) #重建成图片
    plt.imshow(im, cmap=plt.cm.gray,interpolation ='nearest', clim=(0,1))
    plt.xlabel(f'{n_components} Components',  fontsize = 12)
    if i == 1:
        plt.title('Original Image', fontsize = 14)
    else:
        plt.title(f'{percentages[i-1]*100}% of Explained Variance', fontsize = 14)
plt.show()

5 sklearn中的其他降维算法函数

from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.decomposition import FactorAnalysis

iris = datasets.load_iris()
X_train = iris.data
y_train = iris.target
#PCA降维算法
pca=PCA(n_components=2)
X_pca=pca.fit_transform(X_train)
# print(X_pca)
#T-SNE降维算法
tsne=TSNE(n_components=2)
X_tsne=tsne.fit_transform(X_train)
#LDA，注意此算法是监督降维，需要传入正确结果
LDA=LinearDiscriminantAnalysis(n_components=2)
X_lda=LDA.fit_transform(X_train,y_train)
#FA降维
fa=FactorAnalysis(n_components=2)
X_fa=fa.fit_transform(X_train)

#整理降维后的数据，把第一维和第二维都单抽成列表，方便绘图
def mergeData(data):
    x_list=[]
    y_list=[]
    for i in range(len(data)):
        x_list.append(data[i][0])
        y_list.append(data[i][1])
    return x_list,y_list
fig=plt.figure()
ax1=fig.add_subplot(2,2,1)
ax2=fig.add_subplot(2,2,2)
ax3=fig.add_subplot(2,2,3)
ax4=fig.add_subplot(2,2,4)
(x_pca,y_pca)=mergeData(X_pca)
(x_tsne,y_tsne)=mergeData(X_tsne)
(x_lda,y_lda)=mergeData(X_lda)
(x_fa,y_fa)=mergeData(X_fa)
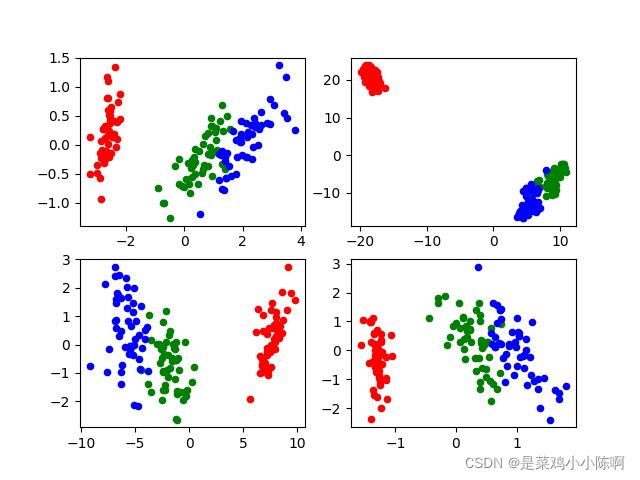
#把3类鸢尾花降维后的数据标成不同的颜色，方便比较降维效果
ax1.scatter(x_pca[0:50],y_pca[0:50],s=20,color='red')
ax1.scatter(x_pca[50:100],y_pca[50:100],s=20,color='green')
ax1.scatter(x_pca[100:],y_pca[100:],s=20,color='blue')
ax2.scatter(x_tsne[0:50],y_tsne[0:50],s=20,color='red')
ax2.scatter(x_tsne[50:100],y_tsne[50:100],s=20,color='green')
ax2.scatter(x_tsne[100:],y_tsne[100:],s=20,color='blue')
ax3.scatter(x_lda[0:50],y_lda[0:50],s=20,color='red')
ax3.scatter(x_lda[50:100],y_lda[50:100],s=20,color='green')
ax3.scatter(x_lda[100:],y_lda[100:],s=20,color='blue')
ax4.scatter(x_fa[0:50],y_fa[0:50],s=20,color='red')
ax4.scatter(x_fa[50:100],y_fa[50:100],s=20,color='green')
ax4.scatter(x_fa[100:],y_fa[100:],s=20,color='blue')

plt.show()

https://blog.csdn.net/baidu_38406307/article/details/103846581?spm=1001.2014.3001.5501
https://github.com/datawhalechina/machine-learning-toy-code/blob/main/ml-with-sklearn/PCA/PCA.ipynb

6 sklearn中的fit、transform、fit_transform、inverse_transform

1. 数据预处理中方法

fit(): Method calculates the parameters μ and σ and saves them as internal objects.
解释：简单来说，就是求得训练集X的均值，方差，最大值，最小值,这些训练集X固有的属性。

transform(): Method using these calculated parameters apply the transformation to a particular dataset.
解释：在fit的基础上，进行标准化，降维，归一化等操作（看具体用的是哪个工具，如PCA，StandardScaler等）。

fit_transform(): joins the fit() and transform() method for transformation of dataset.
解释：fit_transform是fit和transform的组合，既包括了训练又包含了转换。
transform()和fit_transform()二者的功能都是对数据进行某种统一处理（比如标准化~N(0,1)，将数据缩放(映射)到某个固定区间，归一化，正则化等）

fit_transform(trainData)对部分数据先拟合fit，找到该part的整体指标，如均值、方差、最大值最小值等等（根据具体转换的目的），然后对该trainData进行转换transform，从而实现数据的标准化、归一化等等。

https://blog.csdn.net/weixin_38278334/article/details/82971752

2. 各种算法的方法

以PCA为例
1、fit(X,y=None)

fit(X)，表示用数据X来训练PCA模型。

函数返回值：调用fit方法的对象本身。比如pca.fit(X)，表示用X对pca这个对象进行训练。

拓展：fit()可以说是scikit-learn中通用的方法，每个需要训练的算法都会有fit()方法，它其实就是算法中的“训练”这一步骤。因为PCA是无监督学习算法，此处y自然等于None。

2、fit_transform(X)

用X来训练PCA模型，同时返回降维后的数据。

newX=pca.fit_transform(X)，newX就是降维后的数据。

3、inverse_transform()

将降维后的数据转换成原始数据，X=pca.inverse_transform(newX)

4、transform(X)

将数据X转换成降维后的数据。当模型训练好后，对于新输入的数据，都可以用transform方法来降维。

import numpy as np
from sklearn.decomposition import PCA
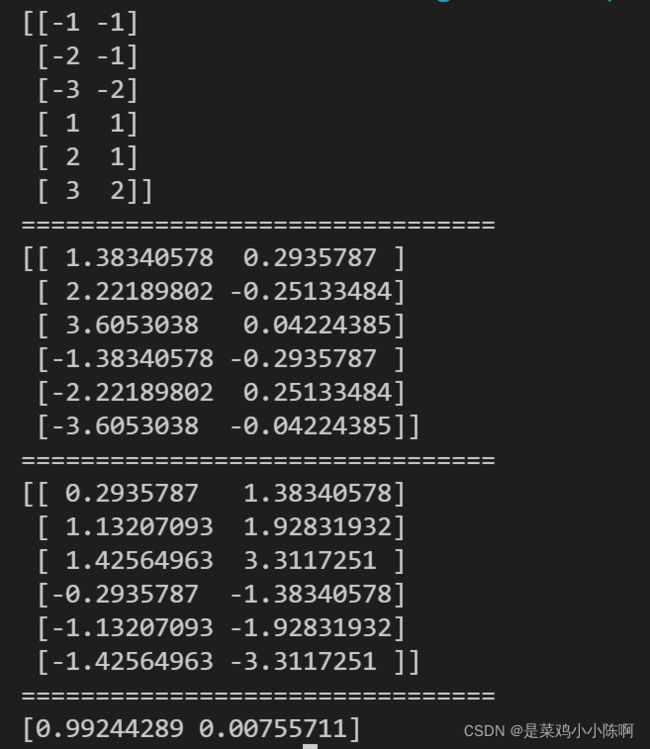
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
newX = pca.fit_transform(X)     #等价于pca.fit(X) pca.transform(X)
invX = pca.inverse_transform(X)  #将降维后的数据转换成原始数据
print(X)
print("================================")
print(newX)
print("================================")
print(invX)
print("================================")
print(pca.explained_variance_ratio_)

https://blog.csdn.net/qq_20135597/article/details/95247381