记录学习数据分析入门（1）——泰坦尼克Titanic（超详细！）

背景介绍

Titanic数据集是非常适合数据科学和机器学习新手入门练习的数据集。

数据集为1912年泰坦尼克号沉船事件中一些船员的个人信息以及存活状况。这些历史数据已经非分为训练集和测试集，可以根据训练集训练出合适的模型并预测测试集中的存活状况。

数据集下载地址（如果kaggle下载慢，可以用这个）

来源于 和鲸社区: 泰坦尼克数据集下载.
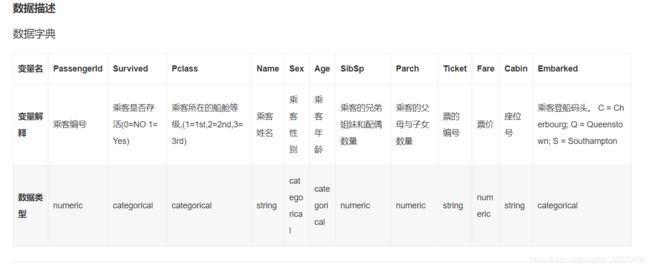
这个网站对于数据集的各个特征有很详细的数据描述。

一.数据基本情况的了解

import pandas as pd
titanic=pd.read_csv('train.csv')
titanic.head(3)
print(titanic.describe())
print(titanic.info())

这里通过pandas，将csv文件读出DataFrame数据形式。
输出结果

      PassengerId    Survived      Pclass         Age       SibSp  \
count   891.000000  891.000000  891.000000  714.000000  891.000000   
mean    446.000000    0.383838    2.308642   29.699118    0.523008   
std     257.353842    0.486592    0.836071   14.526497    1.102743   
min       1.000000    0.000000    1.000000    0.420000    0.000000   
25%     223.500000    0.000000    2.000000   20.125000    0.000000   
50%     446.000000    0.000000    3.000000   28.000000    0.000000   
75%     668.500000    1.000000    3.000000   38.000000    1.000000   
max     891.000000    1.000000    3.000000   80.000000    8.000000   

            Parch        Fare  
count  891.000000  891.000000  
mean     0.381594   32.204208  
std      0.806057   49.693429  
min      0.000000    0.000000  
25%      0.000000    7.910400  
50%      0.000000   14.454200  
75%      0.000000   31.000000  
max      6.000000  512.329200  
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId    891 non-null int64
Survived       891 non-null int64
Pclass         891 non-null int64
Name           891 non-null object
Sex            891 non-null object
Age            714 non-null float64
SibSp          891 non-null int64
Parch          891 non-null int64
Ticket         891 non-null object
Fare           891 non-null float64
Cabin          204 non-null object
Embarked       889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB
None

输出不是太整齐，关于这里呢，如果把print去掉，就是很整齐的表格形式啦~如图所示：

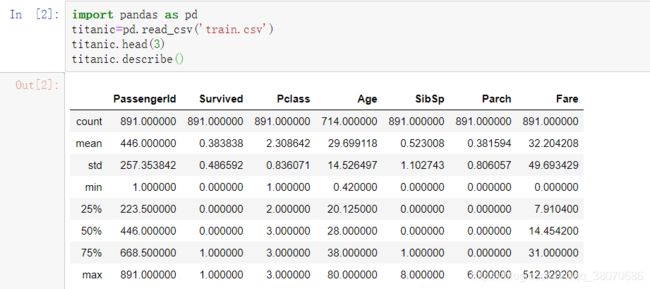
describe函数

查看输出结果，运用了describe函数，总结数据集分布的中心趋势，分散和形状，不包括NaN值。
DataFrame.describe(percentiles=None,include=None,exclude=None)，
可以快速的求出一些算术运算指标。其中其他很容易理解，std代表标准差。
include包含all、[np.number]和[np.object]三个值，describe属性可以对数值型变量（include=[‘number’]）和离散型变量（include=[‘object’]）进行描述性统计。

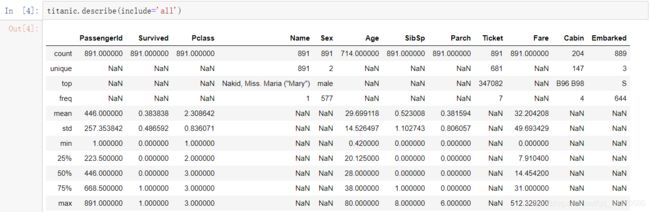
(1)include=‘all’

print(titanic.describe(include='all'))

 PassengerId    Survived      Pclass                         Name  \
count    891.000000  891.000000  891.000000                          891   
unique          NaN         NaN         NaN                          891   
top             NaN         NaN         NaN  Nakid, Miss. Maria ("Mary")   
freq            NaN         NaN         NaN                            1   
mean     446.000000    0.383838    2.308642                          NaN   
std      257.353842    0.486592    0.836071                          NaN   
min        1.000000    0.000000    1.000000                          NaN   
25%      223.500000    0.000000    2.000000                          NaN   
50%      446.000000    0.000000    3.000000                          NaN   
75%      668.500000    1.000000    3.000000                          NaN   
max      891.000000    1.000000    3.000000                          NaN   

         Sex         Age       SibSp       Parch  Ticket        Fare    Cabin  \
count    891  714.000000  891.000000  891.000000     891  891.000000      204   
unique     2         NaN         NaN         NaN     681         NaN      147   
top     male         NaN         NaN         NaN  347082         NaN  B96 B98   
freq     577         NaN         NaN         NaN       7         NaN        4   
mean     NaN   29.699118    0.523008    0.381594     NaN   32.204208      NaN   
std      NaN   14.526497    1.102743    0.806057     NaN   49.693429      NaN   
min      NaN    0.420000    0.000000    0.000000     NaN    0.000000      NaN   
25%      NaN   20.125000    0.000000    0.000000     NaN    7.910400      NaN   
50%      NaN   28.000000    0.000000    0.000000     NaN   14.454200      NaN   
75%      NaN   38.000000    1.000000    0.000000     NaN   31.000000      NaN   
max      NaN   80.000000    8.000000    6.000000     NaN  512.329200      NaN   

       Embarked  
count       889  
unique        3  
top           S  
freq        644  
mean        NaN  
std         NaN  
min         NaN  
25%         NaN  
50%         NaN  
75%         NaN  
max         NaN  

这里的freq代表着频次。

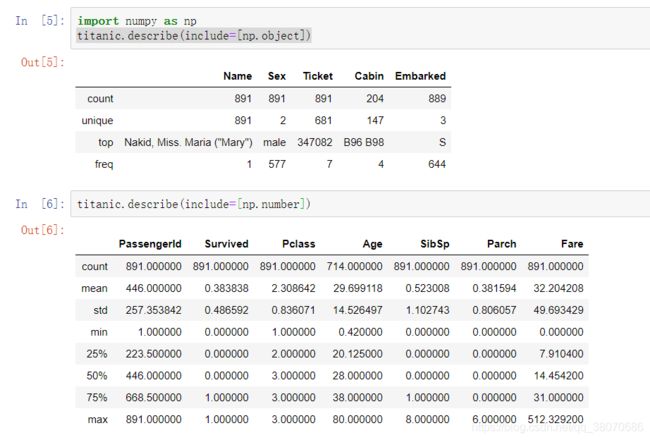
(2)include=np.object/number

import numpy as np
titanic.describe(include=[np.object])

titanic.describe(include=[np.number])

info函数

dataframe.info()函数用于获取 DataFrame 的简要摘要。在对数据进行探索性分析时，它非常方便。为了快速浏览数据集，我们使用dataframe.info()功能。

1.用法：

DataFrame.info(verbose=None, buf=None, max_cols=None, memory_usage=None, null_counts=None)

2.参数分析：

-verbose:是否打印完整的摘要。屏幕上将不显示任何内容。
-max_info_columns设置。 True或False会覆盖显示。max_info_columns设置。
-buf:可写缓冲区，默认为sys.stdout
-max_cols:确定是打印完整摘要还是简短摘要。屏幕上将不显示任何内容。max_info_columns设置。
-memory_usage:指定是否应显示DataFrame元素(包括索引)的总内存使用情况。屏幕上将不显示任何内容。memory_usage设置。 True或False会覆盖显示。memory_usage设置。 “ deep”的值与True相同，具有自省性。内存使用情况以人类可读的单位(以2为基数的表示形式)显示。
-null_counts：是否显示非空计数。如果为None，则仅显示框架是否小于max_info_rows和max_info_columns。如果为True，则始终显示计数。如果为False，则从不显示计数。

(1)DataFrame的完整摘要

titanic.info()

输出：

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId    891 non-null int64
Survived       891 non-null int64
Pclass         891 non-null int64
Name           891 non-null object
Sex            891 non-null object
Age            714 non-null float64
SibSp          891 non-null int64
Parch          891 non-null int64
Ticket         891 non-null object
Fare           891 non-null float64
Cabin          204 non-null object
Embarked       889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB

(2)DataFrame的简短摘要

可以使用verbose参数并将其设置为False

titanic.info(verbose=False)

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Columns: 12 entries, PassengerId to Embarked
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB

(3)打印 DataFrame 的完整摘要，并排除null-counts。

titanic.info(verbose=True,null_counts=False

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId    int64
Survived       int64
Pclass         int64
Name           object
Sex            object
Age            float64
SibSp          int64
Parch          int64
Ticket         object
Fare           float64
Cabin          object
Embarked       object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB

正如我们在输出中看到的那样，摘要已满，但null-counts被排除在外。

分析

通过info()函数所输出的各个特征值的个数，PassengerId：891，Survived：891 ，Pclass：891 ，Name：891，Sex：891，Age：714，SibSp： 891，Parch：891，Ticket：891 ，Fare：891，Cabin：204，Embarked：889，一共有891个乘客，但是Age、Cabin、Embarked数量值不够，需要进行缺失值填充。在这里还要注意数据类型，Name、Sex、Ticket、Cabin、Embarked都是object数据类型，机器学习不能处理，需要将它们转化为机器学习能处理的类型。每一次数据分析都需要进行数据预处理。数据预处理是必要的步骤。

二.数据预处理

（来源于知乎一个学姐总结的知识，个人觉得很受用——————最全面的数据预处理介绍 - 宋城的文章 - 知乎链接: 最全面的数据预处理介绍.）

数据预处理相关知识

基本内容

数据是机器学习的原料，在把数据投入机器学习模型前，我们需要对数据进行加工。数据预处理在数据分析各个环节中是非常重要的！数据预处理是机器学习落地最麻烦但最具有挑战的环节。在实际业务处理中，数据通常是脏数据。所以呢，数据预处理又被称为数据清洗。数据在预处理之前可能会存在以下几种问题：

• 1.数据缺失 （Incomplete） 是属性值为空的情况。如 Age= “ ”。
• 2.数据噪声 （Noisy）是数据值不合常理的情况。如 Ticket = “-100”
• 3.数据不一致 （Inconsistent）是数据前后存在矛盾的情况。如 Age = “42” vs. Birthday = “01/09/1985”
• 4.数据冗余 （Redundant）是数据量或者属性数目超出数据分析需要的情况，比如说，Survived的个数为1000。
• 5.数据集不均衡 （Imbalance）是各个类别的数据量相差悬殊的情况。（这里通常会使用归一化来使它们的数据量级更接近）
• 6.离群点/异常值 （Outliers）是远离数据集中其余部分的数据。比如说，一群儿童里面有一位老奶奶，他们的年龄相差较多。
• 7.数据重复（Duplicate）是在数据集中出现多次的数据。

主要步骤

• 1.数据清洗 Data Cleansing
• 2.数据转换 Data Transformation
• 3.数据描述 Data Description
• 4.特征选择 Feature Selection 或特征组合 Feature Combination
• 5.特征抽取 Feature Extraction

1.数据清洗

在数据清洗阶段，我们处理第一部分提及的缺失数据、离群点和重复数据。

缺失数据

在这个泰坦尼克数据集中，主要是对于缺失数据做处理。
主要有以下几类：

• 1.Missing completely at random（随机缺失）: 缺失的概率是随机的，比如门店的计数器因为断电断网等原因在某个时段数据为空。
• 2.Missing conditionally at random（其他属性相关缺失）: 数据是否缺失取决于另外一个属性，比如一些女生不愿意填写自己的体重。
• 3.Not missing at random（自身属性相关确实）: 数据缺失与自身的值有关，比如高收入的人可能不愿意填写收入。
  处理方式有以下几种：
• a. 删数据，如果缺失数据的记录占比比较小，直接把这些记录删掉完事。
• b. 手工填补，或者重新收集数据，或者根据领域知识来补数据。
• c. 自动填补，简单的就是均值填充，或者再加一个概率分布看起来更真实些，也可以结合实际情况通过公式计算，比如门店计数缺失，可以参考过往的客流数据，转化数据，缺失时段的销售额，用一个简单公式自动计算回补。

离群点

离群点是远离数据集中其余部分的数据，这部分数据可能由随机因素产生，也可能是由不同机制产生。如何处理取决于离群点的产生原因以及应用目的。若是由随机因素产生，我们忽略或者剔除离群点；若是由不同机制产生，离群点就是宝贝，是应用的重点。后者的一个应用为异常行为检测，如在银行的信用卡诈骗识别中，通过对大量的信用卡用户信息和消费行为进行向量化建模和聚类，发现聚类中远离大量样本的点显得非常可疑，因为他们和一般的信用卡用户特性不同，他们的消费行为和一般的信用卡消费行为也相去甚远。还有购物网站检测恶意刷单等场景也重点对离群点进行分析。
不论是对离群点提出还是重点研究应用，我们首先需要检测出离群点。在sklearn(一个python机器学习包)中提供了多种方法，如OneClassSVM、Isolation Forest、Local Outlier Factor (LOF)。

重复数据

对重复数据的处理如下：如果高度疑似的样本是挨着的，就可以用滑动窗口对比，为了让相似记录相邻，可以每条记录生成一个hash key, 根据key去排序。（这是数据结构的内容哦~哈希表，应该都记得吧）

在数据清洗阶段结束后，我们得到的就是没有错误的数据集了~

2.数据转换

在数据转换阶段，我们对数据进行采样处理、类型转换、归一化。
在泰坦尼克数据集中，主要进行了数据的类型转换

采样处理

采样是从特定的概率分布中抽取样本点的过程。
采样在机器学习中有非常重要的应用：将复杂分布简化为离散的样本点；用重采样可以对样本集进行调整以更好地进行调整并适应后期的模型学习；用于随机模拟以进行复杂模型的近似求解或推理。采样的一个重要作用是处理不均衡数据集。
最简单的处理不均衡样本集的方法是随机采样。采样一般分为过采样（Over-sampling）和欠采样（Under-sampling）。随机过采样是从少数类样本集 S_min中有放回地随机重复抽取样本，随机欠采样是从多数类样本集S_max中随机选取较少样本。两种方法也存在问题，如随机过采样会扩大数据规模，容易造成过拟合；随机欠采样可能损失部分有用信息，造成欠拟合。为了解决上诉问题，通常在随机过采样时不是简单复制样本，而是采取一定方法生成新的样本。如使用SMOTE（Synthetic Minority Oversampling Technique）算法、Borderline-SMOTE、ADASYN等算法。对于欠采样，可以采用Informed Undersampling来解决数据丢失问题。
PS：当总体数据量不够时，除了简化模型，我们可以借鉴随机过采样的方法，对每个类进行过采样。具体到图像任务，还可以直接在图像空间进行变换，如可以通过对图像施加一定幅度的变换（旋转、平移、缩放、裁剪、填充、翻转、添加噪声、颜色变换、改变亮度、清晰度、对比度等），得到扩充的数据集。此外，迁移学习也是在小数据集上进行建模的好方法。
PS：整体准确率不适用于不平衡数据集，需要引入新的度量模式比如G-mean, 它会看正类上的准确率，再看负类上的准确率，然后两者相乘取平方根。另外一种常见的度量如F-score

类型转换

数据类型可以简单划分为数值型和非数值型。数值型有连续型和离散型。非数值型有类别型和非类别型，其中类别型特征中如果类别存在排序问题为定序型，若不存在排序问题则为定类型，非类别型是字符串型。如下所示：

• 1.连续型 Continuous（比如说）

Real values: Temperature, Height, Weight …

• 2.离散型 Discrete（比如说兄弟姐妹个数）

Integer values: Number of people …

• 3.定序型 Ordinal（比如说泰坦尼克号船舱等级）

Rankings: {Average, Good, Best}, {Low, Medium, High} …

• 4.定类型 Nominal（比如说泰坦尼克是否获救）

Symbols: {Teacher, Worker, Salesman}, {Red, Green, Blue} …

• 5.字符串型 String

Text: “Tsinghua University”, “No. 123, Pingan Avenue”
……
对于非数值型，我们需要进行类别转换，即将非数值型转换为数值型，以方便机器学习算法后续处理。
对于定序型，我们可以使用序号编码，如成绩，分为Average, Good, Best三档，序号编码可以按照大小关系对定序型特征赋予一个数值ID，例如Average表示为1，Good表示为2，Best表示为3，转换后依旧保留了大小关系。
对于定类型，我们可以使用独热编码，如颜色三原色，为Red, Green, Blue，独热编码可以把三原色变为一个三维稀疏向量，Red表示为（0，0，1），Green表示为（0，1，0），Blue表示为（1，0，0）。需要注意的是，在类别值较多的情况下，可以使用稀疏向量来节省空间，目前大部分算法实现均接受稀疏向量形式的输入。当然还有很多别的编码方式，如二进制编码等，感兴趣的可以额外查阅资料了解。
对于字符串型，我们有多种表示方式，如词袋模型（Bag of Words），TF-IDF（Term Frequency-Inverse），主题模型（Topic Model），词嵌入模型（Word Embedding）。各种表示有不同的适用场景和优缺点，需要进一步了解的可以额外查资料。

归一化

经过类别转换后，我们所有的数据均转为了数值型。为了消除数据特征之间的量纲影响，我们需要对特征进行归一化处理，使不同指标之间具有可比性。
例如，分析一个人的身高和体重对健康的影响，如果使用米（m）和千克（kg）作为单位，身高在1.6-1.8m的数值范围内，体重特征在50-100kg的数值范围内，分析出来的结果会倾向于数值差别较大的体重特征。对数值型特征进行归一化可以将所有特征都统一到一个大致相同的区间内，以便进行分析。归一化方式通常有线性函数归一化（Min-Max Scaling）和零均值归一化（Z-score Normalization）。
当然，不是所有的机器学习算法需要对数值进行归一化，在实际应用中，通过梯度下降法求解的模型通常需要归一化，因为经过归一化后，梯度在不同特征上更新速度趋于一致，可以加快模型收敛速度。而决策树模型并不需要，以C4.5为例，决策树在节点分裂时主要依据数据集D关于特征x的信息增益比，而信息增益比跟特征是否经过归一化是无关的。

3.数据描述

在数据描述阶段，我们可以根据需要计算统计量和对数据进行可视化。

数据的一般性描述有mean, median, mode, variance.
mean是均值；median是中位数，取数据排序后在中间位置的值，避免因为极端离群点影响客观评价；mode是出现频率最高的元素，其实用的比较少；variance是方差衡量数据集与其均值的偏离。
数据之间的相关性可以使用Pearson correlation coefficient和Pearson chi-square进行度量。前者适用与有metric data的情况，后者适用于分类统计的情况。
数据可视化一维数据圆饼图，柱状图；二维数据散点图；三维数据用三维坐标呈现；高维数据需要先做转换或映射，比如用matlab的Box Plots，也可以用平行坐标呈现。可使用工具有很多，如matlab和Geph。

4.特征选择

当我们做特定分析的时候，可能属性非常多，但有些属性是不相关的，有些属性是重复的，所以我们需要用特征选择挑选出来最相关的属性降低问题难度。

我们可以通过熵增益(Entropy Information Gain)、分支定界（Branch and Bound）等方式进行特征选择。特征选择还有sequential forward, sequential backward, simulated annealing(模拟退火), tabu search(竞技搜索), genetic algorithms(遗传算法)等方式去优化。

为了提高复杂关系的拟合能力，在特征工程中经常会把一些离散特征两两组合，构成高阶特征。如在点击率预测问题中，原始数据有语言和类型两种特征，为了提高拟合能力，语言和类型可以组合成二阶特征，联合预测对点击率的影响。如何找到有意义的组合特征？有一种方法是基于决策树的组合特征寻找方法。

5.特征抽取

在机器学习中，数据通常需要表示为向量的形式进行训练，但是在对高维向量进行处理和分析时，会极大消耗系统资源，甚至产生维度灾难。因此，使用低维度的向量来表示高维度的向量就十分必要。特征抽取或降维即使用低纬度向量表示高维度向量的方法。

特征抽取是主要有主成分分析（Principal Component Analysis，PCA）和线性判别分析（Linear Discriminant Analysis，LDA）两种方式。两者相同之处为均假设数据服从高斯分布，都使用了矩阵分解的思想。两者不同之处为PCA是无监督的算法，对降低后的维度无限制，其目标为投影方差最大；LDA是有监督的算法，降维后的维度小于类别数，其目标为类内方差最小，类间方差最大。

Titanic数据预处理

主要是针对于数据缺失这个问题来进行数据清洗，针对于特征Age、Sex、Embarked。

1.Age离散数据缺失值填充

缺失值填充一般用到fillna()函数，分两种情况：
1.如果是数值类型，用平均值或中位数取代
2.如果是分类数据，用最常见的类别取代

#用中值填补Age的空缺值
titanic['Age']=titanic['Age'].fillna(titanic['Age'].median())

fillna()函数

DataFrame.fillna(self, value=None, method=None, axis=None, inplace=False, limit=None, downcast=None, **kwargs)
使用指定的方法填充NA/NaN值。

• value ：scalar(标量), dict, Series, 或DataFrame用于填充孔的值（例如0），或者是dict / Series / DataFrame的值，该值指定用于每个索引（对于Series）或列（对于DataFrame）使用哪个值。不在dict / Series / DataFrame中的值将不被填充。该值不能是列表(list)。
• method ： {‘backfill’，‘bfill’，‘pad’，‘ffill’，None}，默认为None填充重新索引的系列填充板/填充中的holes的方法：将最后一个有效观察向前传播到下一个有效回填/填充：使用下一个有效观察来填充间隙。
• axis ： {0或’index’，1或’columns’}填充缺失值所沿的轴。
• inplace ：bool，默认为False如果为True，则就地填充。注意：这将修改此对象上的任何其他视图（例如，DataFrame中列的无副本切片）。
• limit ：int，默认值None如果指定了method，则这是要向前/向后填充的连续NaN值的最大数量。换句话说，如果存在连续的NaN数量大于此数量的缺口，它将仅被部分填充。如果未指定method，则这是将填写NaN的整个轴上的最大条目数。如果不为None，则必须大于0。
• downcast ： dict，默认为Noneitem->dtype的字典，如果可能的话，将向下转换，或者是字符串“infer”，它将尝试向下转换为适当的相等类型（例如，如果可能，则从float64到int64）。

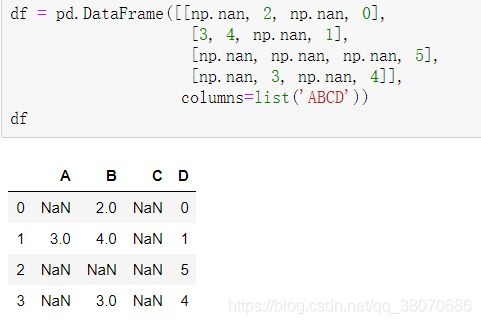
定义一个DataFrame类型的df

df = pd.DataFrame([[np.nan, 2, np.nan, 0],
                    [3, 4, np.nan, 1],
                    [np.nan, np.nan, np.nan, 5],
                    [np.nan, 3, np.nan, 4]],
                   columns=list('ABCD'))
df

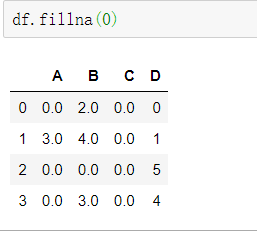
• 将所有NaN元素替换为0

 df.fillna(0)

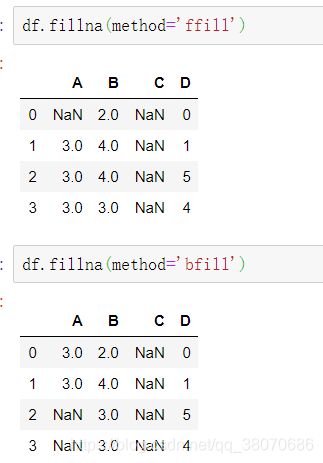
向前或者向后传播非空值

 df.fillna(method='ffill')#向前
 df.fillna(method='bfill')#向后

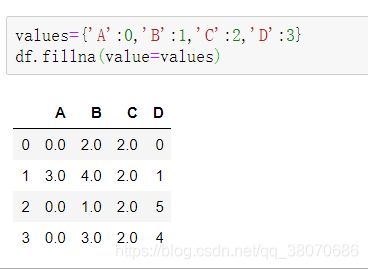
将“ A”，“ B”，“ C”和“ D”列中的所有NaN元素分别替换为0、1、2和3

values={'A':0,'B':1,'C':2,'D':3}
df.fillna(value=values)

仅替换第一个NaN元素

values={'A':0,'B':1,'C':2,'D':3}
df.fillna(value=values,limit=1)

2.Sex数据类型转换

titanic['Sex'].unique()

titanic.loc[titanic['Sex']=='male','Sex']=0
titanic.loc[titanic['Sex']=='female','Sex']=1
titanic['Sex'].unique()

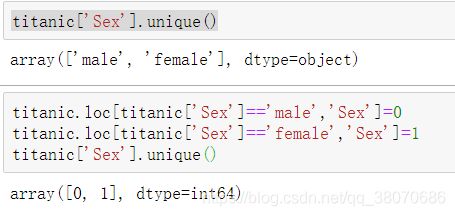
在这里需要注意函数unique()的用法，
转载自unique()用法

• a = np.unique(A)这个函数就是对于一维数组或者列表unique函数去除其中重复的元素，并按元素由大到小返回一个新的无元素重复的元组或者列表。
• c,s=np.unique(b,return_index=True)
  return_index=True表示返回新列表元素在旧列表中的位置，并以列表形式储存在s中。
• a, s,p = np.unique(A, return_index=True, return_inverse=True)
  return_inverse=True 表示返回旧列表元素在新列表中的位置，并以列表形式储存在p中

以及loc[]的用法：
titanic.loc[0]表示第0行的样本
titanic.loc[0, ‘PassengerId’]表示行为0，列为PassengerId的值

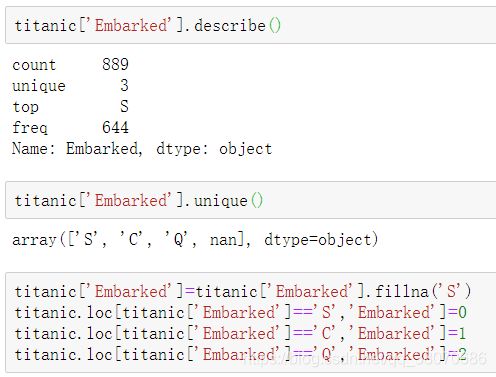
3.Embarked缺失值填充以及数据类型转换

Embarked这一列有缺失值，用最常见的类别即‘S’填充，然后再将数据转化为int型。

titanic['Embarked'].describe()
titanic['Embarked'].unique()
titanic['Embarked'] = titanic['Embarked'].fillna('S')
titanic.loc[titanic['Embarked'] == 'S', 'Embarked'] = 0
titanic.loc[titanic['Embarked'] == 'C', 'Embarked'] = 1
titanic.loc[titanic['Embarked'] == 'Q', 'Embarked'] = 2

三.特征工程

特征工程相关知识

这个博客里面“特征工程”讲的很详细
特征工程指的是把原始数据转变为模型的训练数据的过程，它的目的就是获取更好的训练数据特征，使得机器学习模型逼近这个上限。
主要包括特征构建、特征提取、特征选择。
特征提取强调通过特征转换的方式得到一组具有明显物理或统计意义的特征；而特征选择是从特征集合中挑选一组具有明显物理或统计意义的特征子集。

1.特征构建

特征构建是指从原始数据中人工的找出一些具有物理意义的特征。需要花时间去观察原始数据，思考问题的潜在形式和数据结构，对数据敏感性和机器学习实战经验能帮助特征构建。除此之外，属性分割和结合是特征构建时常使用的方法。结构性的表格数据，可以尝试组合二个、三个不同的属性构造新的特征，如果存在时间相关属性，可以划出不同的时间窗口，得到同一属性在不同时间下的特征值，也可以把一个属性分解或切分，例如将数据中的日期字段按照季度和周期后者一天的上午、下午和晚上去构建特征。

2.特征提取

（1） PCA主成分分析

吴恩达B站视频，推荐机器学习小白看一看哦~
PCA的思想是通过坐标轴转换，寻找数据分布的最优子空间，从而达到降维、去相关的目的。

（2） LDA线性判别分析

PDA与LDA详细介绍
LDA的原理是将带上标签的数据（点），通过投影的方法，投影到维度更低的空间，使得投影后的点，会形成按类别区分，相同类别的点，将会在投影后更接近，不同类别的点距离越远。

PCA与LDA，两者的思想和计算方法非常类似，但是LDA是作为独立的算法存在，PCA更多的用于数据的预处理的工作。LDA的输入数据是带标签的，而PCA的输入数据是不带标签的，所以PCA是一种unsupervised learning。LDA通常来说是作为一个独立的算法存在，给定了训练数据后，将会得到一系列的判别函数（discriminate function），之后对于新的输入，就可以进行预测了。而PCA更像是一个预处理的方法，它可以将原本的数据降低维度，而使得降低了维度的数据之间的方差最大（也可以说投影误差最小，具体在之后的推导里面会谈到）。

(3) ICA独立成分分析

PCA特征转换降维，提取的是不相关的部分，ICA独立成分分析，获得的是相互独立的属性。ICA算法本质寻找一个线性变换z = Wx，使得z的各个特征分量之间的独立性最大。ICA相比与PCA更能刻画变量的随机统计特性，且能抑制噪声。

3.特征选择

特征选择是剔除不相关或者冗余的特征，减少有效特征的个数，减少模型训练的时间，提高模型的精确度。特征提取通过特征转换实现降维，特征选择则是依靠统计学方法或者于机器学习模型本身的特征选择（排序）功能实现降维。特征选择是个重复迭代的过程，有时可能自己认为特征选择做的很好，但实际中模型训练并不太好，所以每次特征选择都要使用模型去验证，最终目的是为了获得能训练出好的模型的数据，提升模型的性能。

(1)运用统计学的方法，衡量单个特征与响应变量（Lable）之间的关系。

①皮尔森相关系数（Pearson Correlation）

衡量变量之间的线性关系，结果取值为[-1,1]，-1表示完全负相关，+1表示正相关，0表示不线性相关，但是并不表示没有其它关系。Pearson系数有一个明显缺陷是，只衡量线性关系，如果关系是非线性的，即使连个变量具有一一对应的关系，Pearson关系也会接近0。皮尔森系数的公式为样本共变异数除以X的标准差和Y的标准差的乘积。

②最大信息系数（MIC）

信息系数MIC不仅能像Pearson系数一样度量变量之间的线性关系，还能度量变量之间的非线性关系。MIC虽然能度量变量之间的非线性关系，但当变量之间的关系接近线性相关的时候，Pearson相关系数仍然是不可替代的。

(2) 基于机器学习模型的特征选择

①线性模型和正则化

当特征和响应变量之间全部都是线性关系，并且特征之间均是比较独立的。可以尝试使用线性回归模型去做特征选择，因为越是重要的特征在模型中对应的系数就会越大，而跟输出变量越是无关的特征对应的系数就会越接近与0。

②随机森林模型

随机森林由多棵决策树构成，决策树中的每个节点，都是关于某个特征的条件，利用不纯度可以确定划分数据集的最优特征，对于分类问题，通常采用基尼不纯度或者信息增益，对于回归问题，通常采用方差或者最小二乘拟合。当训练决策树的时候，可以计算出每个特征减少了多少树的不纯度。对于一个决策树森林来说，可以算出每个特征平均减少了多少不纯度，并把它平均减少的不纯度作为特征选择的值。

另一种常用的特征选择方法就是直接度量每个特征对模型精确率的影响。主要思路是打乱每个特征的特征值顺序，并且度量顺序变动对模型的精确率的影响。很明显，对于不重要的变量来说，打乱顺序对模型的精确率影响不会太大，但是对于重要的变量来说，打乱顺序就会降低模型的精确率。

要记住：1、这种方法存在偏向，对具有更多类别的变量会更有利；2、对于存在关联的多个特征，其中任意一个都可以作为指示器（优秀的特征），并且一旦某个特征被选择之后，其他特征的重要度就会急剧下降，因为不纯度已经被选中的那个特征降下来了，其他的特征就很难再降低那么多不纯度了，这样一来，只有先被选中的那个特征重要度很高，其他的关联特征重要度往往较低。在理解数据时，这就会造成误解，导致错误的认为先被选中的特征是很重要的，而其余的特征是不重要的，但实际上这些特征对响应变量的作用确实非常接近的（这跟Lasso是很像的）。

Titanic特征工程

在这个数据集中，提炼的3个新特征为FamilySize：SibSp和Parch的人数相加，看看是否家庭人数越多获救几率越大；NameLength：名字长度，外国名字越长地位越高；Title：在Name里提取的，类似Mr、Mrs、Dr表示性别职业。
re.search():扫描整个字符串并返回第一个成功的匹配，如果没有成功匹配则返回None。
关于正则表达式：https://www.jb51.net/article/15707.htm

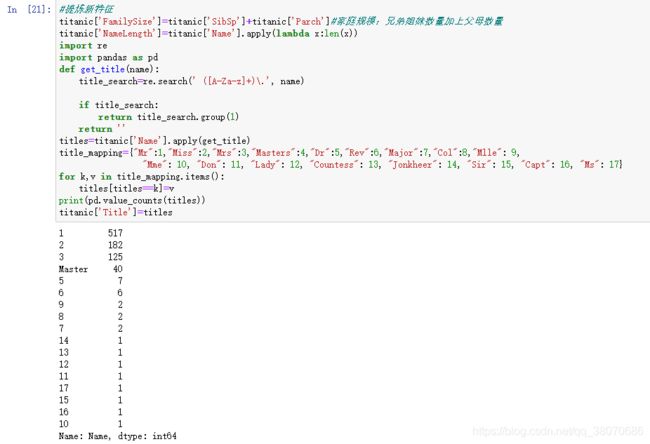
#提炼新特征
titanic['FamilySize']=titanic['SibSp']+titanic['Parch']#家庭规模：兄弟姐妹数量加上父母数量
titanic['NameLength']=titanic['Name'].apply(lambda x:len(x))
import re
import pandas as pd
def get_title(name):
    title_search=re.search(' ([A-Za-z]+)\.', name)
    
    if title_search:
        return title_search.group(1)
    return ''
titles=titanic['Name'].apply(get_title)
title_mapping={"Mr":1,"Miss":2,"Mrs":3,"Masters":4,"Dr":5,"Rev":6,"Major":7,"Col":8,"Mlle": 9,
                 "Mme": 10, "Don": 11, "Lady": 12, "Countess": 13, "Jonkheer": 14, "Sir": 15, "Capt": 16, "Ms": 17}
for k,v in title_mapping.items():
    titles[titles==k]=v
print(pd.value_counts(titles))
titanic['Title']=titles

SelectKBest()：https://blog.csdn.net/sunshunli/article/details/82051138

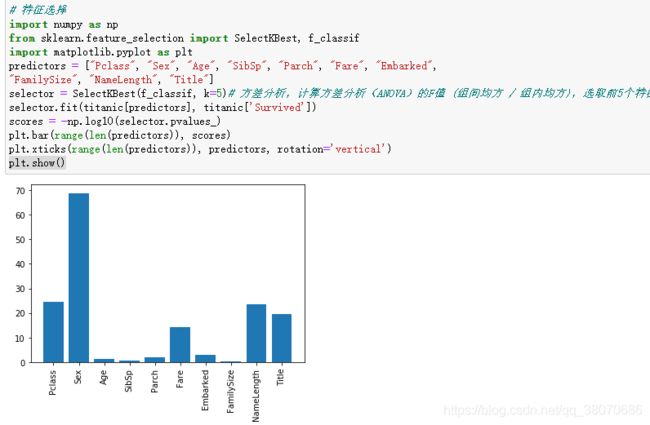
import numpy as np
from sklearn.feature_selection import SelectKBest, f_classif
import matplotlib.pyplot as plt
predictors = ["Pclass", "Sex", "Age", "SibSp", "Parch", "Fare", "Embarked", 
"FamilySize", "NameLength", "Title"]
selector = SelectKBest(f_classif, k=5)# 方差分析，计算方差分析（ANOVA）的F值 (组间均方 / 组内均方)，选取前5个特征
selector.fit(titanic[predictors], titanic['Survived'])
scores = -np.log10(selector.pvalues_)
plt.bar(range(len(predictors)), scores)
plt.xticks(range(len(predictors)), predictors, rotation='vertical')
plt.show()

四.基准模型

机器学习基础知识可以去B站社区找资源。

1.线性回归（最简单的回归）

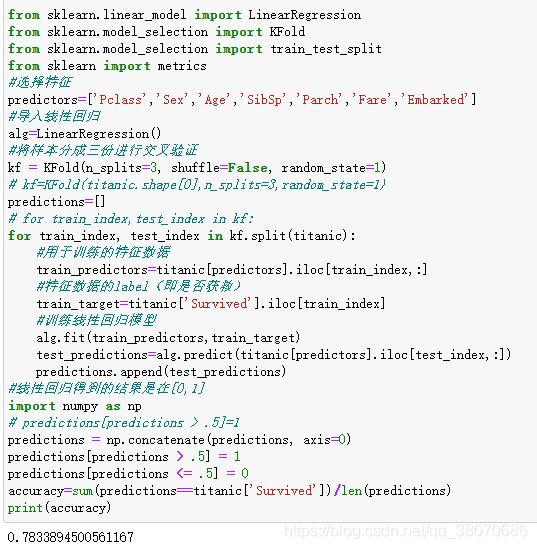
```python
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import KFold
from sklearn.model_selection import train_test_split
from sklearn import metrics
#选择特征
predictors=['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked']
#导入线性回归
alg=LinearRegression()
#将样本分成三份进行交叉验证
kf = KFold(n_splits=3, shuffle=False, random_state=1)
# kf=KFold(titanic.shape[0],n_splits=3,random_state=1)
predictions=[]
# for train_index,test_index in kf:
for train_index, test_index in kf.split(titanic):
    #用于训练的特征数据
    train_predictors=titanic[predictors].iloc[train_index,:]
    #特征数据的label（即是否获救）
    train_target=titanic['Survived'].iloc[train_index]
    #训练线性回归模型
    alg.fit(train_predictors,train_target)   
    test_predictions=alg.predict(titanic[predictors].iloc[test_index,:])
    predictions.append(test_predictions)
#线性回归得到的结果是在[0,1]
import numpy as np
# predictions[predictions > .5]=1
predictions = np.concatenate(predictions, axis=0)
predictions[predictions > .5] = 1
predictions[predictions <= .5] = 0
accuracy=sum(predictions==titanic['Survived'])/len(predictions)
print(accuracy)

如图：

2.逻辑回归

函数：cross_val_score(model_name, X,y， cv=k)
参数：1、模型函数名，如 LogisticRegression()2、训练集 3、测试属性 4、K折交叉验证
作用：验证某个模型在某个训练集上的稳定性，输出k个预测精度。

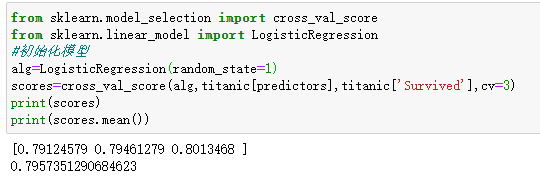
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
#初始化模型
alg=LogisticRegression(random_state=1)
scores=cross_val_score(alg,titanic[predictors],titanic['Survived'],cv=3)
print(scores)
print(scores.mean())

3.随机森林

随机森林的随机体现在两点：1、取样本是随机的，且是有放回的 2、特征的选择是随机的，不一定所有的属性特征都要用到。森林表示生成多个决策树

函数：RandomForestClassifier()
参数解释：random_state = 1 表示此处代码多运行几次得到的随机值都是一样的，如果不设置，两次执行的随机值是不一样的；n_estimators=50 表示有50棵决策树；树的分裂的条件是: min_samples_split =4代表样本不停的分裂，某一个节点上的样本如果只有4个了 ，就不再继续分裂了；min_samples_leaf =2表示叶子节点的最小个数为2。

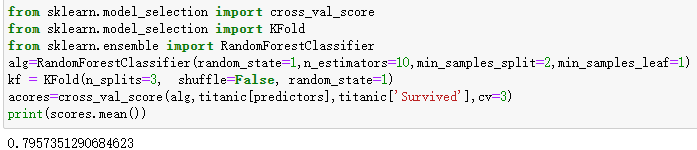
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier
alg=RandomForestClassifier(random_state=1,n_estimators=10,min_samples_split=2,min_samples_leaf=1)
kf = KFold(n_splits=3,  shuffle=False, random_state=1)
acores=cross_val_score(alg,titanic[predictors],titanic['Survived'],cv=3)
print(scores.mean())

五.混合模型

混合模型是在竞赛中常用的办法：集成多个模型，得出每个模型的结果，并赋予每个模型权重，求出最后的平均结果。
关于混合模型呢，是时序预测方面经常可以想到的解决方法。
上面的基准模型发现逻辑回归和随机森林效果更好，所以我集成了这两种模型。如果发现某个模型更好，权重可以更高(案例中随机森林权重是2，逻辑回归的是1)

from sklearn.ensemble import GradientBoostingClassifier 
import numpy as np
algorithms=[
    [RandomForestClassifier(random_state=1,n_estimators=20,min_samples_split=4,min_samples_leaf=2),
     ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked', 'FamilySize', 'NameLength', 'Title']],
    [LogisticRegression(random_state=1),
     ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked', 'FamilySize', 'NameLength', 'Title']]
]
kf = KFold(n_splits=11, shuffle=False)
predictions=[]
for train,test in kf.split(titanic):
    train_target=titanic['Survived'].iloc[train]
    full_test_prediction=[]
    for alg,predictors in algorithms:
        alg.fit(titanic[predictors].iloc[train,:],train_target)
        test_prediction=alg.predict_proba(titanic[predictors].iloc[test,:].astype(float))[:,1]
        full_test_prediction.append(test_prediction)
    #使用集成模型
    test_predictions=(full_test_prediction[0]*2+full_test_prediction[1]*1)/3
    test_predictions[test_predictions>.5]=1
    test_predictions[test_predictions<=.5]=0
    predictions.append(test_predictions)
predictions=np.concatenate(predictions,axis=0)
accuracy=sum(predictions==titanic['Survived'])/len(predictions)
print(accuracy)

运行结果：