C++ 数据结构 二叉排序树/二叉查找树

---

前言

今天在学习红黑树的时候，看到了引导课拿二叉排序树举例，想到之前还没写过二叉排序树的代码，所以这次特地写了一下，这里把二叉排序树的性质和写代码时出现的问题做一个分享。

概念

介绍

在写之前，要先了解什么是二叉排序树

二叉查找树，它有一个根节点，且每个节点下最多有只能有两个子节点，左子节点的值小于其父节点，右子节点的值大于其父节点。

我们依次插入数据：43,98,2,4,0,5
下图就是插入完成后二叉查找树的样子

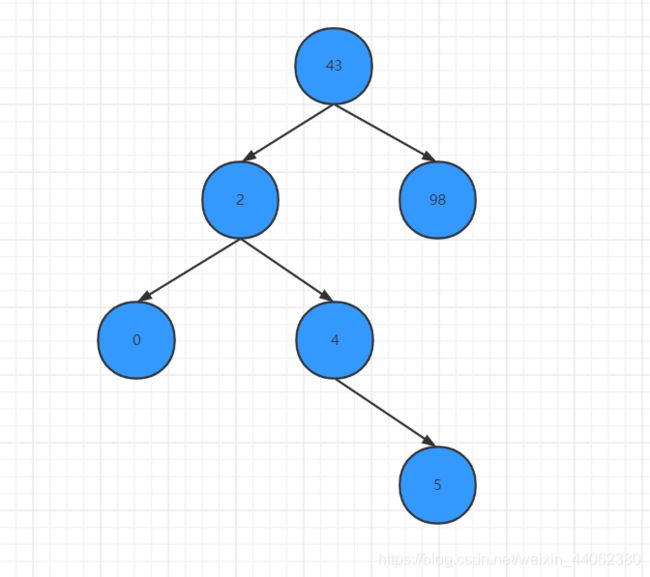
数据操作无非是增删改查
对于二叉排序树
增就是insert节点
删就是delete节点
查就是查询值x是否存在于树中

二叉排序树存在意义的思考

这时候有人可能会问了：“查找用数组不香吗？一个for循环搞定”。
这里我们来分析一波时间复杂度
for循环遍历数组，最坏情况是遍历到最后一个元素，时间复杂度为O(n)
而二叉查找树的查找方式类似于二分查找，只要查找树的高度，我们都知道，查找树高的时间复杂度为O(logn)

这时候可能又有人要问了：“既然时间复杂度都是O(logn)，那我直接二分查找不就好了？还要建树那么麻烦。”
问的好，但是我们再想想，二分查找前，要先对数组进行排序，我们如果用排序速度较快的归并或者快排，时间复杂度为O(nlogn)，再加上二分查找的时间复杂度O(logn)（这里我们还没谈在数组中插入数据的时间复杂度和可能需要扩容的麻烦） ,也就是说，在最恶劣的情况下，第一次的查询时间是二叉排序树的两倍还多。

这时候可能又有读者骂我避重就轻了，“你说排序要时间，那你建树不要时间吗？”
骂的好，建树花费的时间和空间复杂度我们先不谈，我们谈谈 增 这个操作。
对于排好序的数组，在其中插入一个数据，不用再重新排序，只要遍历一遍就好，时间复杂度为O(n);
但对于二叉排序树，插入一个新数据，因为插入前要遍历的长度最长就是树的高度，所以时间复杂度为O(logn)，插入一个数据可能效果还不明显，但插入10个，10000个，1亿个呢？很明显，从长期来看，二叉排序树的时间花费是明显优于使用二分查找的。

说了这么多，干货还一点没讲，下面我们进入正题！

操作以及代码展示

插入元素

根据二叉排序树的特点，我们很容易就能想出插入数据的思路，如果插入节点小于对比节点，且对比节点的左枝为空，就插在对比节点的左枝上，如果不为空，就对对比节点的左枝进行相同的插入操作（递归）；如果插入节点比对比节点大，操作是一样的，就是换个方向。
对过程稍微分析一下，我们就知道要用到递归，代码如下

void BinSearchTree::insert(int x)
{
	/*
	这个重载是为了插入方便
	只要insert一个值就可以了
	不用自己再新建节点
	*/
	Node *root=new Node(x);
	if(this->Root==NULL)
	{
		this->Root=root;
		return;
	}
	Node *p=this->Root;
	insert(p,root);
}

void BinSearchTree::insert(Node *p,Node *root)
{
	/*
	可不可以有相同的元素要根据需求来
	如果不要相同元素，最好在用户插入的时候说明
	如果有相同，插左边还是右边都可以，但定下左右就不能改了
	这里我写的时候就简单一点，遇到相同的就不插了
	*/

	//学了点算法，感觉写起来没以前难了（滑稽）
	if(root->data==p->data) return;//遇到相同，直接不插入
	if(root->data < p->data)
	{
		if(p->lChild==NULL)
		{
			p->lChild=root;
			return;
		}
		else insert(p->lChild,root);
	}
	else//root->data > p->data
	{
		if(p->rChild==NULL)
		{
			p->rChild=root;
			return;
		}
		else insert(p->rChild,root);
	}
}

可不可以有相同的元素要根据需求来
如果不要相同元素，最好在用户插入的时候说明
如果有相同，插左边还是右边都可以，但定下左右就不能改了
这里我写的时候就简单一点，遇到相同的就不插了

查找元素

这里我写了两个
一个是用来查找元素在不在查找树中
一个是用来返回拥有该值的节点
因为我的树设定的是没有相同元素，所以不存在找到多个元素的问题

查找元素在不在查找树中

bool BinSearchTree::search(int x)
{
	if(x==this->Root->data) return true;
	Node *p=this->Root;
	return search(p,x);
}

bool BinSearchTree::search(Node *p,int x)
{
	if(p==NULL) return false;//找到空的地方都没有，说明真没有
	if(p->data==x) return true;
	if(x<p->data) search(p->lChild,x);
	else search(p->rChild,x);
}

返回拥有该值的节点

Node * BinSearchTree::searchNode(int x)
{
	if(this->Root->data==x) return this->Root;
	Node *p=this->Root;
	return searchNode(p,x);
}

Node * BinSearchTree::searchNode(Node *p,int x)
{
	if(p->data==x) return p;
	if(x<p->data) return searchNode(p->lChild,x);
	else return searchNode(p->rChild,x);
}

删除元素

删除一共分三种情况
1.删除的节点左右孩子都有
2.删除的节点只有一个孩子
3.删除的节点没有孩子

对于
情况1.将要删除节点的右孩子中的最小节点与要删除节点的值替换
这样就将该问题变成了情况2 或者 情况3
情况2.被删除节点的父节点指向被删除节点的子节点，然后删除该节点
情况3.直接删除该节点

ps:为什么第一种情况要取右子树的最小值？这其实十分巧妙
首先，作为待删节点的右子树，肯定比待删节点的左子树大
其次，作为待删节点右子树的最小子树数，比待删节点所有的右子树节点小
所以其代替待删节点最好

void BinSearchTree::removeNode(int x)
{
	/*
	删除节点一共有三种情况
	1.删除的节点左右孩子都有
	2.删除的节点只有一个孩子
	3.删除的节点没有孩子

	对于
	1.将要删除节点的右孩子中的最小节点与要删除节点的值替换
	这样就将该问题变成了情况2 或者 情况3
	2.被删除节点的父节点指向被删除节点的子节点，然后删除该节点
	3.直接删除该节点

	ps:为什么第一种情况要取右子树的最小值？这其实十分巧妙
	首先，作为待删节点的右子树，肯定比待删节点的左子树大
	其次，作为待删节点右子树的最小子树数，比待删节点所有的右子树节点小
	所以其代替待删节点最好
	*/
	Node *p=searchNode(x);//找到待删除节点
	if(p->lChild==NULL && p->rChild==NULL) withNoChild(p);
	else if(p->lChild!=NULL && p->rChild!=NULL) withTwoChild(p);
	else withOneChild(p);
	return;
}

void BinSearchTree::withTwoChild(Node *p)//因为withOneChile有毛病，所以它也有毛病<---withOneChild好像没毛病
{//应该是它本身的毛病
	//情况1，将要删除节点的右孩子中的最小节点与要删除节点的值替换
	//这样就将该问题变成了情况2 或者 情况3
	Node *min=getMinNode(p->rChild);
	std::cout<<"右子树最小值为:";
	std::cout<<min->data<<std::endl;

	int minVal=min->data;

	if(min->lChild==NULL && min->rChild==NULL) withNoChild(min);
	else withOneChild(min);//<======我知道为什么会出问题了,当改了待删节点的数值后，就会出现两个min值
	//找父节点就会起冲突
	//所以应该先删在改

	p->data=minVal;//<-----要先删再改，不然会出现问题!!!
}

void BinSearchTree::withOneChild(Node *p)//有毛病<---貌似也没有毛病
{
	Node *father=getFather(p);
	Node *child;
	if(p->lChild==NULL) child=p->rChild;
	else child=p->lChild;

	//如果待删节点是其父节点的左孩子
	if(father->lChild->data==p->data) father->lChild=child;
	//如果待删节点是其父节点的右孩子
	else father->rChild=child;
	delete p;
}

void BinSearchTree::withNoChild(Node *p)//没毛病
{
	Node *father=getFather(p);
	std::cout<<father->data<<std::endl;
	if(father->lChild->data==p->data) father->lChild=NULL;
	else father->rChild=NULL;
	delete p;
}

运行结果

这里我们输入例子中的数字 43,98,2,4,0,5 来构造二叉排序树

广度优先结果符合理论结构

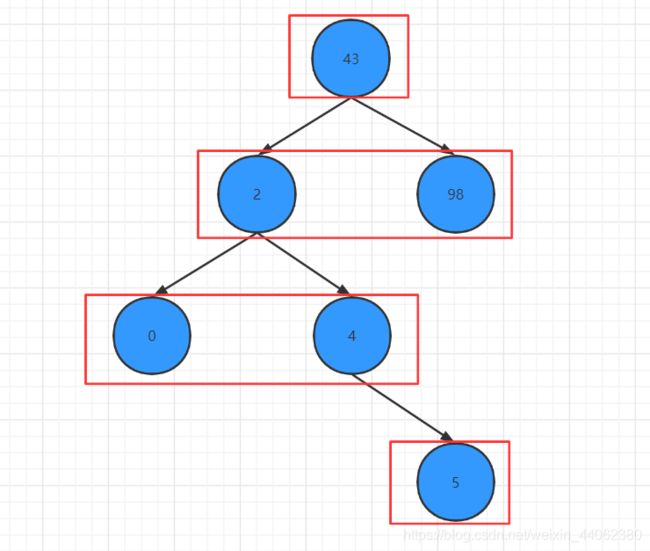
这里我们再删除节点 2

删除过程如下



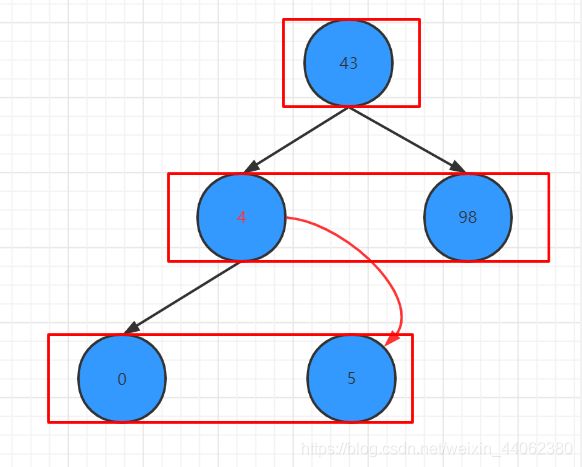
如上图，删除完成后的树进行层次遍历，其结果与理论结果相等，可以大致确认我的代码应该是正确的。

二叉排序树的优缺点及解决方法

优点

优点我在二叉排序树存在意义那一栏多有涉及，这里就不再赘述了

缺点

在谈缺点前，我们来看看下面这个图

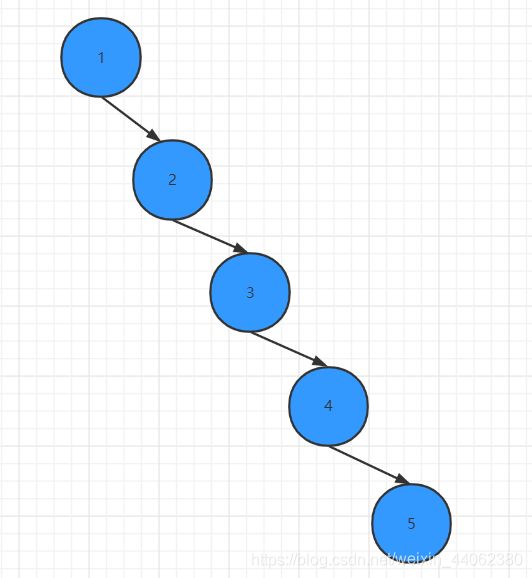
有没有发现什么问题？没错，这也是个二叉排序是，只是成了一个瘸子。当插入的数据递增或者递减的时候，二叉排序树就成了一个链表，查找的时间复杂度退化为O(n)，这不是我们想要的结果

解决方案

那该怎么解决这个问题呢？ 这就涉及高级数据结构 红黑树了

有人可能会问了：“帖主你怎么不讲了？”，其实红黑树我还没看，等我学完了在来分享吧，嘻嘻。

-------------------------------------------------------- 6.17 更新 --------------------------------------------------------------
我学成归来了，红黑树的分享在这里