本文首发于我的知乎专栏:https://zhuanlan.zhihu.com/p/484657229
实验概览
Cache Lab 分为两部分,编写一个高速缓存模拟器以及要求优化矩阵转置的核心函数,以最小化对模拟的高速缓存的不命中次数。本实验对我这种代码能力较差的人来说还是很有难度的。
在开始实验前,强烈建议先阅读以下学习资料:
实验说明文档:Writeup
CMU 关于 Cache Lab 的 PPT:Cache Lab Implementation and Blocking
CMU 关于分块优化的讲解: Using Blocking to Increase Temporal Locality
本人踩的坑:我的 lab 环境是 Windows11 + wsl2。由于 wsl2 跨 OS 磁盘访问非常慢,而我是将文件放在 Windows 下进行的实验,Part B 部分的测试结果甚至无法跑出来!所以,建议用虚拟机进行实验,如果你也是 wsl2 用户,请将实验文件放在 wsl2 自己的目录下!
Part A: Writing a Cache Simulator
Part A 要求在csim.c下编写一个高速缓存模拟器来对内存读写操作进行正确的反馈。这个模拟器有 6 个参数:
Usage: ./csim-ref [-hv] -s -E -b -t
• -h: Optional help flag that prints usage info
• -v: Optional verbose flag that displays trace info
• -s : Number of set index bits (S = 2s is the number of sets)
• -E : Associativity (number of lines per set)
• -b : Number of block bits (B = 2b is the block size)
• -t : Name of the valgrind trace to replay
其中,输入的 trace 的格式为:[space]operation address, size,operation 有 4 种:
I表示加载指令L加载数据S存储数据M修改数据
模拟器不需要考虑加载指令,而M指令就相当于先进行L再进行S,因此,要考虑的情况其实并不多。模拟器要做出的反馈有 3 种:
hit:命中,表示要操作的数据在对应组的其中一行miss:不命中,表示要操作的数据不在对应组的任何一行eviction:驱赶,表示要操作的数据的对应组已满,进行了替换操作
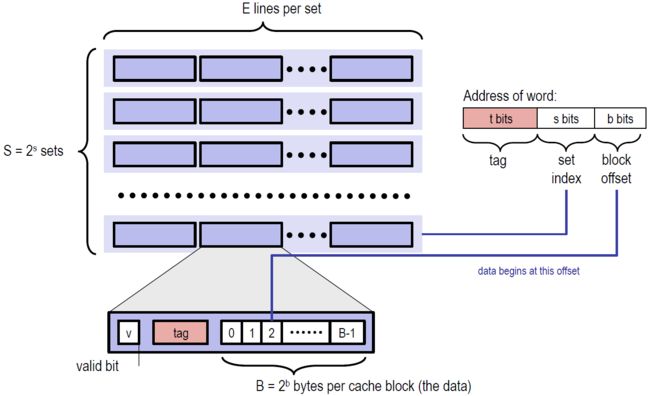
回顾:Cache 结构
Cache 类似于一个二维数组,它有\(S=2^s\)组,每组有 E 行,每行存储的字节也是固定的。其中,每行都有一个有效位,和一个标记位。想要查找到对应的字节,我们的地址需要三部分组成:
- s,索引位,找到对应的组序号
- tag,标记位,在组中的每一行进行匹配,判断能否命中
- b,块偏移,表明在找到的行中的具体位置。本实验不考虑块便宜,完全可以忽略。
那么,Cache 中的有效位是干什么的呢?判断该行是否为空。这里有一个概念:冷不命中,表示该缓存块为空造成的不命中。而一旦确定不命中不是冷不命中,那么就需要考虑行替换的问题了。我认为,行替换关乎着 Cache 的效率,是 Cache 设计的核心。
回顾:替换策略
当 CPU 要处理的字不在组中任何一行,且组中没有一个空行,那就必须从里面选取一个非空行进行替换。选取哪个空行进行替换呢?书上给了我们两种策略:
- LFU,最不常使用策略。替换在过去某个窗口时间内引用次数最少的那一行
- LRU,最近最少使用策略。替换最后一次访问时间最久远的哪一行
本实验要求采取的策略为 LRU。
那么代码如何实现呢?我的第一反应是实现 S 个双向链表,每个链表有 E 个结点,对应于组中的每一行,每当访问了其中的一行,就把这个结点移动到链表的头部,后续替换的时候只需要选择链尾的结点就好了。但是,为了简单,我还是选择了 PPT 中提示的相对简单的设置时间戳的办法,双向链表以后有时间再写吧。
下面就可以正式开始 Part A 了!我对我写的模拟器的核心部分进行讲解。
数据结构
定义了Cache结构体
typedef struct cache_
{
int S;
int E;
int B;
Cache_line **line;
} Cache;
用Cache表示一个缓存,它包括 S, B, E 等特征,以及前面说过的,每一个缓存类似于一个二位数组,数组的每一个元素就是缓存中的行所以用一个line来表示这一信息:
typedef struct cache_line
{
int valid; //有效位
int tag; //标记位
int time_tamp; //时间戳
} Cache_line;
valid以及tag不再赘述,这里的time_tamp表示时间戳,是 LRU 策略需要用到的特征。Cache 初始值设置如下:
void Init_Cache(int s, int E, int b)
{
int S = 1 << s;
int B = 1 << b;
cache = (Cache *)malloc(sizeof(Cache));
cache->S = S;
cache->E = E;
cache->B = B;
cache->line = (Cache_line **)malloc(sizeof(Cache_line *) * S);
for (int i = 0; i < S; i++)
{
cache->line[i] = (Cache_line *)malloc(sizeof(Cache_line) * E);
for (int j = 0; j < E; j++)
{
cache->line[i][j].valid = 0; //初始时,高速缓存是空的
cache->line[i][j].tag = -1;
cache->line[i][j].time_tamp = 0;
}
}
}
注意,时间戳初始设置为0。
LRU 时间戳实现
我的逻辑是时间戳越大则表示该行最后访问的时间越久远。先看 LRU 更新的代码:
void update(int i, int op_s, int op_tag){
cache->line[op_s][i].valid=1;
cache->line[op_s][i].tag = op_tag;
for(int k = 0; k < cache->E; k++)
if(cache->line[op_s][k].valid==1)
cache->line[op_s][k].time_tamp++;
cache->line[op_s][i].time_tamp = 0;
}
这段代码在找到要进行的操作行后调用(无论是不命中还是命中,还是驱逐后)。前两行是对有效位和标志位的设置,与时间戳无关,主要关注后几行:
- 遍历组中每一行,并将它们的值加1,也就是说每一行在进行一次操作后时间戳都会变大,表示它离最后操作的时间变久
- 将本次操作的行时间戳设置为最小,也就是0
由此,每次只需要找到时间戳最大的行进行替换就可以了:
int find_LRU(int op_s)
{
int max_index = 0;
int max_stamp = 0;
for(int i = 0; i < cache->E; i++){
if(cache->line[op_s][i].time_tamp > max_stamp){
max_stamp = cache->line[op_s][i].time_tamp;
max_index = i;
}
}
return max_index;
}
缓存搜索及更新
先解决比较核心的问题,在得知要操作的组op_s以及标志位op_tag后,判断是miss还是hit还是应该eviction调用find_LRU。
先判断是miss还是hit:
int get_index(int op_s, int op_tag)
{
for (int i = 0; i < cache->E; i++)
{
if (cache->line[op_s][i].valid && cache->line[op_s][i].tag == op_tag)
return i;
}
return -1;
}
遍历所有行,如果某一行有效,且标志位相同,则hit,返回该索引。否则,miss,返回 -1。当接收到-1后,有两种情况:
- 冷不命中。组中有空行,只不过还未操作过,有效位为0,找到这个空行即可
- 所有行都满了。那么就要用到上面得 LRU 进行选择驱逐
所以,设计一个判满的函数:
int is_full(int op_s)
{
for (int i = 0; i < cache->E; i++)
{
if (cache->line[op_s][i].valid == 0)
return i;
}
return -1;
}
扫描完成后,得到对应行的索引值,就可以调用 LRU 更新函数进行更新了。整体调用如下:
void update_info(int op_tag, int op_s)
{
int index = get_index(op_s, op_tag);
if (index == -1)
{
miss_count++;
if (verbose)
printf("miss ");
int i = is_full(op_s);
if(i==-1){
eviction_count++;
if(verbose) printf("eviction");
i = find_LRU(op_s);
}
update(i,op_s,op_tag);
}
else{
hit_count++;
if(verbose)
printf("hit");
update(index,op_s,op_tag);
}
}
至此,Part A 的核心部分函数就编写完了,下面的内容属于是技巧性的部分,与架构无关。
指令解析
设计的数据结构解决了对 Cache 的操作问题,LRU 时间戳的实现解决了核心的驱逐问题,缓存扫描解决了对块中哪一列进行操作的问题,而应该对哪一块进行操作呢?接下来要解决的就是指令的解析问题了。
输入数据为[space]operation address, size的形式,operation很容易获取,重要的是从address中分别获取我们需要的s和tag,address结构如下:
这就用到了第二章以及Data Lab的知识。tag 很容易得到,右移 (b + s) 位即可:
int op_tag = address >> (s + b);
获取 s,考虑先右移 b 位,再用无符号 0xFF... 右移后进行与操作将 tag 抹去。为什么要用无符号 0xFF... 右移呢?因为C语言中的右移为算术右移,有符号数右移补位的数为符号位。
int op_s = (address >> b) & ((unsigned)(-1) >> (8 * sizeof(unsigned) - s));
由于数据读写对于本模拟器而言是没有区别的,因此不同的指令对应的只是 Cache 更新次数的问题:
void get_trace(int s, int E, int b)
{
FILE *pFile;
pFile = fopen(t, "r");
if (pFile == NULL)
{
exit(-1);
}
char identifier;
unsigned address;
int size;
// Reading lines like " M 20,1" or "L 19,3"
while (fscanf(pFile, " %c %x,%d", &identifier, &address, &size) > 0) // I读不进来,忽略---size没啥用
{
//想办法先得到标记位和组序号
int op_tag = address >> (s + b);
int op_s = (address >> b) & ((unsigned)(-1) >> (8 * sizeof(unsigned) - s));
switch (identifier)
{
case 'M': //一次存储一次加载
update_info(op_tag, op_s);
update_info(op_tag, op_s);
break;
case 'L':
update_info(op_tag, op_s);
break;
case 'S':
update_info(op_tag, op_s);
break;
}
}
fclose(pFile);
}
update_info就是对 Cache 进行更新的函数,前面已经讲解。如果指令是M则一次存储一次加载,总共更新两次,其他指令只用更新一次,而I无需考虑。
命令行参数获取
通过阅读Cache Lab Implementation and Blocking的提示,我们使用getopt()函数来获取命令行参数的字符串形式,然后用atoi()转换为要用的参数,最后用switch语句跳转到对应功能块。
代码如下:
int main(int argc, char *argv[])
{
char opt;
int s, E, b;
/*
* s:S=2^s是组的个数
* E:每组中有多少行
* b:B=2^b每个缓冲块的字节数
*/
while (-1 != (opt = getopt(argc, argv, "hvs:E:b:t:")))
{
switch (opt)
{
case 'h':
print_help();
exit(0);
case 'v':
verbose = 1;
break;
case 's':
s = atoi(optarg);
break;
case 'E':
E = atoi(optarg);
break;
case 'b':
b = atoi(optarg);
break;
case 't':
strcpy(t, optarg);
break;
default:
print_help();
exit(-1);
}
}
Init_Cache(s, E, b); //初始化一个cache
get_trace(s, E, b);
free_Cache();
// printSummary(hit_count, miss_count, eviction_count)
printSummary(hit_count, miss_count, eviction_count);
return 0;
}
完整代码太长,可访问我的Github仓库查看:
https://github.com/Deconx/CSAPP-Lab
Part B: Optimizing Matrix Transpose
Part B 是在trans.c中编写矩阵转置的函数,在一个 s = 5, E = 1, b = 5 的缓存中进行读写,使得 miss 的次数最少。测试矩阵的参数以及 miss 次数对应的分数如下:
要求最多只能声明12个本地变量。
根据课本以及 PPT 的提示,这里肯定要使用矩阵分块进行优化
32 × 32
开始之前,我们先了解一下何为分块?为什么分块?
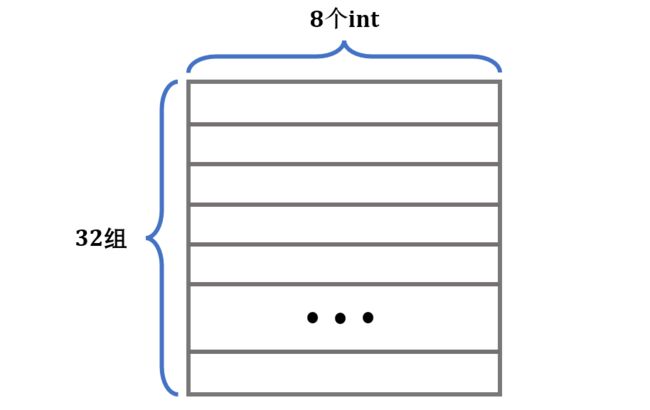
s = 5, E = 1, b = 5 的缓存有32组,每组一行,每行存 8 个int,如图:
就以这个缓存为例,考虑暴力转置的做法:
void trans_submit(int M, int N, int A[N][M], int B[M][N]) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
int tmp = A[i][j];
B[j][i] = tmp;
}
}
}
这里我们会按行优先读取 A 矩阵,然后一列一列地写入 B 矩阵。
以第1行为例,在从内存读 A[0][0] 的时候,除了 A[0][0] 被加载到缓存中,它之后的 A[0][1]---A[0][7] 也会被加载进缓存。
但是内容写入 B 矩阵的时候是一列一列地写入,在列上相邻的元素不在一个内存块上,这样每次写入都不命中缓存。并且一列写完之后再返回,原来的缓存可能被覆盖了,这样就又会不命中。我们来定量分析。
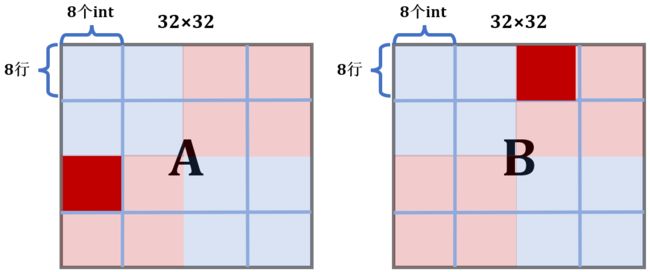
缓存只够存储一个矩阵的四分之一,A中的元素对应的缓存行每隔8行就会重复。A和B的地址由于取余关系,每个元素对应的地址是相同的。各个元素对应缓存行如下:
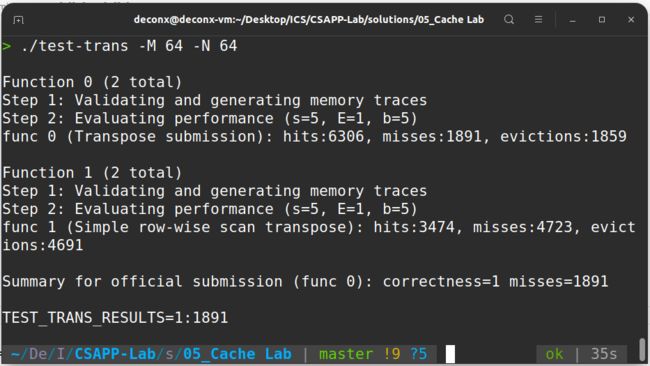
对于A,每8个int就会占满缓存的一组,所以每一行会有 32/8 = 4 次不命中;而对于B,考虑最坏情况,每一列都有 32 次不命中,由此,算出总不命中次数为 4 × 32 + 32 × 32 = 1152。拿程序跑一下:
结果为 1183 比预估多了一点,这是对角线部分两者冲突造成的,后面会讲到。
回过头来,思考暴力做法:
在写入B的前 8 行后,B的D区域就全部进入了缓存,此时如果能对D进行操作,那么就能利用上缓存的内容,不会miss;但是,暴力解法接下来操作的是C,每一个元素的写都要驱逐之前的缓存区,当来到第 2 列继续写D时,它对应的缓存行很可能已经被驱逐了,于是又要miss,也就是说,暴力解法的问题在于没有充分利用上已经进入缓存的元素。
分块解决的就是同一个矩阵内部缓存块相互替换的问题。
由上述分析,显然应考虑 8 × 8 分块,这样在块的内部不会冲突,接下来判断A与B之间会不会冲突
A中标红的块占用的是缓存的第 0,4,8,12,16,20,24,28组,而B中标红的块占用的是缓存的第2,6,10,14,18,16,30组,刚好不会冲突。事实上,除了对角线,A与B中对应的块都不会冲突。所以,我们的想法是可行的,写出代码:
void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
for (int i = 0; i < N; i += 8)
for (int j = 0; j < M; j += 8)
for (int k = 0; k < 8; k++)
for (int s = 0; s < 8; s++)
B[j + s][i + k] = A[i + k][j + s];
}
对于A中每一个操作块,只有每一行的第一个元素会不命中,所以为8次不命中;对于B中每一个操作块,只有每一列的第一个元素会不命中,所以也为 8 次不命中。总共miss次数为:8 × 16 × 2 = 256
跑出结果:
miss次数为343,与我们计算的结果差距非常大,没有得到满分,这是为什么呢?这就要考虑到对角线上的块了。A与B对角线上的块在缓存中对应的位置是相同的,而它们在转置过程中位置不变,所以复制过程中会发生相互冲突。
以A的一个对角线块p,B与p相应的对角线块q为例,复制前, p 在缓存中。 复制时,q会驱逐p。 下一个开始复制 p 又被重新加载进入缓存驱逐 q,这样就会多产生两次miss。
如何解决这种问题呢?题目给了我们提示:
You are allowed to define at most 12 local variables of type int per transpose function
考虑使用 8 个本地变量一次性存下 A 的一行后,再复制给 B。代码如下:
void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
for(int i = 0; i < 32; i += 8)
for(int j = 0; j < 32; j += 8)
for (int k = i; k < i + 8; k++)
{
int a_0 = A[k][j];
int a_1 = A[k][j+1];
int a_2 = A[k][j+2];
int a_3 = A[k][j+3];
int a_4 = A[k][j+4];
int a_5 = A[k][j+5];
int a_6 = A[k][j+6];
int a_7 = A[k][j+7];
B[j][k] = a_0;
B[j+1][k] = a_1;
B[j+2][k] = a_2;
B[j+3][k] = a_3;
B[j+4][k] = a_4;
B[j+5][k] = a_5;
B[j+6][k] = a_6;
B[j+7][k] = a_7;
}
}
对于非对角线上的块,本身就没有额外的冲突;对于对角线上的块,写入A每一行的第一个元素后,这一行的元素都进入了缓存,我们就立即用本地变量存下这 8 个元素,随后再复制给B。这样,就避免了第一个元素复制时,B把A的缓冲行驱逐,导致没有利用上A的缓冲。
结果如下:
miss次数为 287,满分!
64 × 64
每 4 行就会占满一个缓存,先考虑 4 × 4 分块,结果如下:
结果还不错,虽然没有得到满分。
还是考虑 8 × 8 分块,由于存在着每 4 行就会占满一个缓存的问题,在分块内部处理时就需要技巧了,我们把分块内部分成 4 个 4 × 4 的小分块分别处理:
- 第一步,将
A的左上和右上一次性复制给B - 第二步,用本地变量把
B的右上角存储下来 - 第三步,将
A的左下复制给B的右上 - 第四步,利用上述存储
B的右上角的本地变量,把A的右上复制给B的左下 - 第五步,把
A的右下复制给B的右下
画出图解如下:
这里的A和B均表示两个矩阵中的 8 × 8 块
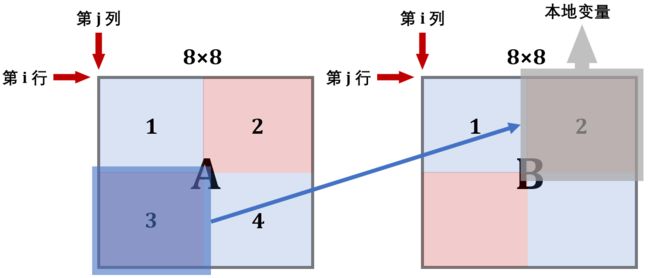
第 1 步:
此时B的前 4 行就在缓存中了,接下来考虑利用这个缓存 。可以看到,为了利用A的缓存,第 2 块放置的位置实际上是错的,接下来就用本地变量保存B中 2 块的内容
第 2 步:
用本地变量把B的 2 块存储下来
for (int k = j; k < j + 4; k++){
a_0 = B[k][i + 4];
a_1 = B[k][i + 5];
a_2 = B[k][i + 6];
a_3 = B[k][i + 7];
}
第 3 步:
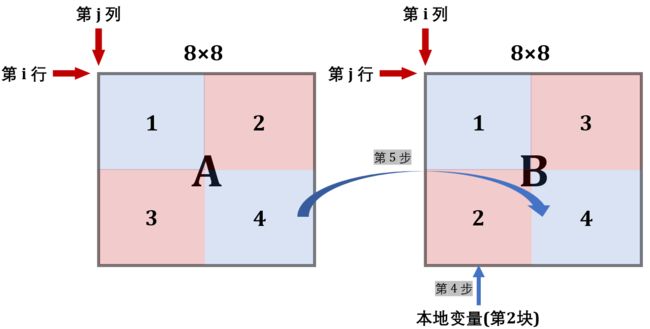
现在缓存中还是存着B中上两块的内容,所以将A的 3 块内容复制给它
第 4/5 步:
现在缓存已经利用到极致了,可以开辟B的下面两块了
这样就实现了转置,且消除了同一行中的冲突,具体代码如下:
void transpose_64x64(int M, int N, int A[N][M], int B[M][N])
{
int a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7;
for (int i = 0; i < 64; i += 8){
for (int j = 0; j < 64; j += 8){
for (int k = i; k < i + 4; k++){
// 得到A的第1,2块
a_0 = A[k][j + 0];
a_1 = A[k][j + 1];
a_2 = A[k][j + 2];
a_3 = A[k][j + 3];
a_4 = A[k][j + 4];
a_5 = A[k][j + 5];
a_6 = A[k][j + 6];
a_7 = A[k][j + 7];
// 复制给B的第1,2块
B[j + 0][k] = a_0;
B[j + 1][k] = a_1;
B[j + 2][k] = a_2;
B[j + 3][k] = a_3;
B[j + 0][k + 4] = a_4;
B[j + 1][k + 4] = a_5;
B[j + 2][k + 4] = a_6;
B[j + 3][k + 4] = a_7;
}
for (int k = j; k < j + 4; k++){
// 得到B的第2块
a_0 = B[k][i + 4];
a_1 = B[k][i + 5];
a_2 = B[k][i + 6];
a_3 = B[k][i + 7];
// 得到A的第3块
a_4 = A[i + 4][k];
a_5 = A[i + 5][k];
a_6 = A[i + 6][k];
a_7 = A[i + 7][k];
// 复制给B的第2块
B[k][i + 4] = a_4;
B[k][i + 5] = a_5;
B[k][i + 6] = a_6;
B[k][i + 7] = a_7;
// B原来的第2块移动到第3块
B[k + 4][i + 0] = a_0;
B[k + 4][i + 1] = a_1;
B[k + 4][i + 2] = a_2;
B[k + 4][i + 3] = a_3;
}
for (int k = i + 4; k < i + 8; k++)
{
// 处理第4块
a_4 = A[k][j + 4];
a_5 = A[k][j + 5];
a_6 = A[k][j + 6];
a_7 = A[k][j + 7];
B[j + 4][k] = a_4;
B[j + 5][k] = a_5;
B[j + 6][k] = a_6;
B[j + 7][k] = a_7;
}
}
}
}
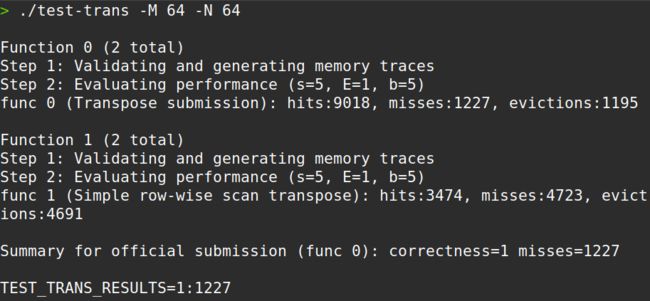
运行结果:
miss为 1227,通过!
61 × 67
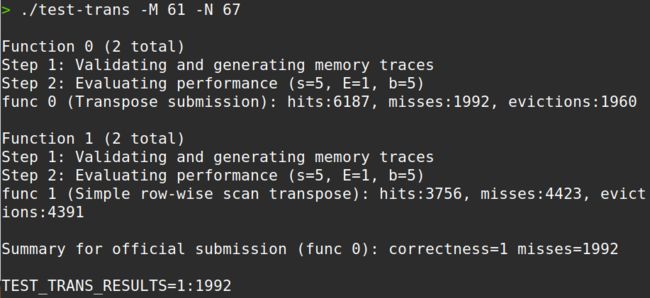
这个矩阵的转置要求很松,miss为 2000 以下就可以了。我也无心进行更深入的优化,直接 16 × 16 的分块就能通过。
miss为 1992,擦线满分!
总结
先附上满分完结图:
- Cache Lab 是我在做前 5 个实验中感觉最痛苦的一个,主要原因在于我的代码能力较弱,逻辑思维能力较差,以后应该加强这方面的训练
- 这个实验的 Part A 让我对缓存的设计有了更深入的理解,其中替换策略也值得以后继续研究;Part B 为我展示了计算机之美,一个简简单单的转置函数,无论怎么写,时间复杂度都是\(O(n^2)\),然而因为缓冲区的问题,不同代码的性能竟然有着天壤之别。编写函数过程中,对
miss的估量与计算很烧脑,但也很有趣 - 本实验耗时 2 天,约 20 小时