【lstm预测】基于粒子群优化lstm预测matlab源码

粒子群算法

粒子群算法是在1995年由Eberhart博士和Kennedy博士一起提出的，它源于对鸟群捕食行为的研究。它的基本核心是利用群体中的个体对信息的共享从而使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的最优解。设想这么一个场景：一群鸟进行觅食，而远处有一片玉米地，所有的鸟都不知道玉米地到底在哪里，但是它们知道自己当前的位置距离玉米地有多远。那么找到玉米地的最佳策略，也是最简单有效的策略就是搜寻目前距离玉米地最近的鸟群的周围区域。

在PSO中，每个优化问题的解都是搜索空间中的一只鸟，称之为"粒子"，而问题的最优解就对应于鸟群中寻找的"玉米地"。所有的粒子都具有一个位置向量(粒子在解空间的位置)和速度向量(决定下次飞行的方向和速度)，并可以根据目标函数来计算当前的所在位置的适应值(fitness value),可以将其理解为距离"玉米地"的距离。在每次的迭代中，种群中的例子除了根据自身的经验(历史位置)进行学习以外，还可以根据种群中最优粒子的"经验"来学习，从而确定下一次迭代时需要如何调整和改变飞行的方向和速度。就这样逐步迭代，最终整个种群的例子就会逐步趋于最优解。

上面的解释可能还比较抽象，下面通过一个简单的例子来进行说明

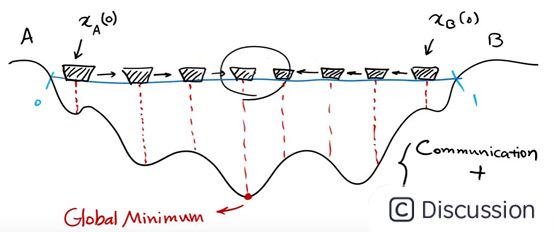
在一个湖中有两个人他们之间可以通信，并且可以探测到自己所在位置的最低点。初始位置如上图所示，由于右边比较深，因此左边的人会往右边移动一下小船。

现在左边比较深，因此右边的人会往左边移动一下小船

一直重复该过程，最后两个小船会相遇

得到一个局部的最优解

将每个个体表示为粒子。每个个体在某一时刻的位置表示为，x(t),方向表示为v(t)

p(t)为在t时刻x个体的自己的最优解，g(t)为在t时刻所有个体的最优解，v(t)为个体在t时刻的方向，x(t)为个体在t时刻的位置

下一个位置为上图所示由x,p,g共同决定了

种群中的粒子通过不断地向自身和种群的历史信息进行学习，从而可以找到问题的最优解。

但是，在后续的研究中表表明，上述原始的公式中存在一个问题：公式中V的更新太具有随机性，从而使整个PSO算法的全局优化能力很强，但是局部搜索能力较差。而实际上，我们需要在算法迭代初期PSO有着较强的全局优化能力，而在算法的后期，整个种群应该具有更强的局部搜索能力。所以根据上述的弊端，shi和Eberhart通过引入惯性权重修改了公式，从而提出了PSO的惯性权重模型：

每一个向量的分量表示如下

其中w称为是PSO的惯性权重，它的取值介于【0,1】区间，一般应用中均采用自适应的取值方法，即一开始令w=0.9，使得PSO全局优化能力较强，随着迭代的深入，参数w进行递减，从而使的PSO具有较强的局部优化能力，当迭代结束时，w=0.1。参数c1和c2称为学习因子，一般设置为1,4961；而r1和r2为介于[0,1]之间的随机概率值。

整个粒子群优化算法的算法框架如下：

step1种群初始化，可以进行随机初始化或者根据被优化的问题设计特定的初始化方法，然后计算个体的适应值，从而选择出个体的局部最优位置向量和种群的全局最优位置向量。

step2 迭代设置：设置迭代次数，并令当前迭代次数为1

step3 速度更新：更新每个个体的速度向量

step4 位置更新：更新每个个体的位置向量

step5 局部位置和全局位置向量更新：更新每个个体的局部最优解和种群的全局最优解

step6 终止条件判断：判断迭代次数时都达到最大迭代次数，如果满足，输出全局最优解，否则继续进行迭代，跳转至step 3。

　　对于粒子群优化算法的运用，主要是对速度和位置向量迭代算子的设计。迭代算子是否有效将决定整个PSO算法性能的优劣，所以如何设计PSO的迭代算子是PSO算法应用的研究重点和难点。

LSTM网络

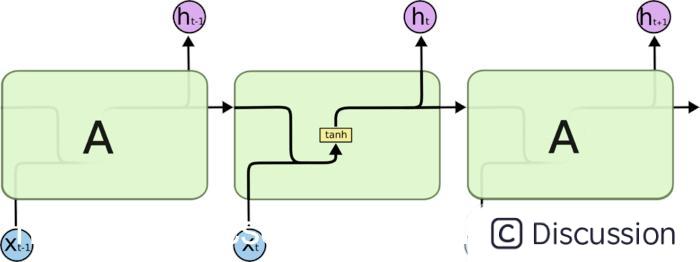
long short term memory，即我们所称呼的LSTM，是为了解决长期以来问题而专门设计出来的，所有的RNN都具有一种重复神经网络模块的链式形式。在标准RNN中，这个重复的结构模块只有一个非常简单的结构，例如一个tanh层。

图3.RNNcell

LSTM 同样是这样的结构，但是重复的模块拥有一个不同的结构。不同于单一神经网络层，这里是有四个，以一种非常特殊的方式进行交互。

图4.LSTMcell

LSTM核心思想

LSTM的关键在于细胞的状态整个(绿色的图表示的是一个cell)，和穿过细胞的那条水平线。

细胞状态类似于传送带。直接在整个链上运行，只有一些少量的线性交互。信息在上面流传保持不变会很容易。

图5.LSTMcell内部结构图

若只有上面的那条水平线是没办法实现添加或者删除信息的。而是通过一种叫做 门(gates) 的结构来实现的。

门 可以实现选择性地让信息通过，主要是通过一个 sigmoid 的神经层 和一个逐点相乘的操作来实现的。

图6.信息节点

sigmoid 层输出(是一个向量)的每个元素都是一个在 0 和 1 之间的实数，表示让对应信息通过的权重(或者占比)。比如， 0 表示“不让任何信息通过”， 1 表示“让所有信息通过”。

LSTM通过三个这样的基本结构来实现信息的保护和控制。这三个门分别输入门、遗忘门和输出门。

深入理解LSTM

遗忘门

在我们 LSTM 中的第一步是决定我们会从细胞状态中丢弃什么信息。这个决定通过一个称为忘记门层完成。该门会读取h t − 1 h_{t−1}ht−1​和x t x_txt​，输出一个在 0到 1之间的数值给每个在细胞状态C t − 1 C_{t-1}Ct−1​中的数字。1 表示“完全保留”，0 表示“完全舍弃”。

其中ht−1表示的是上一个cell的输出，xt表示的是当前细胞的输入。σσ表示sigmod函数。

输入门

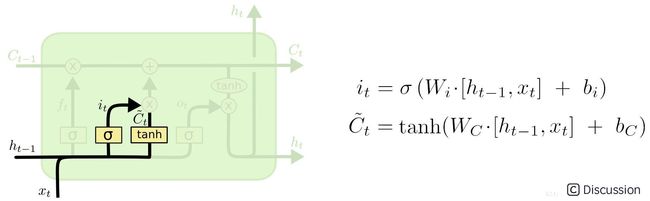
下一步是决定让多少新的信息加入到 cell 状态 中来。实现这个需要包括两个 步骤：首先，一个叫做“input gate layer ”的 sigmoid 层决定哪些信息需要更新；一个 tanh 层生成一个向量，也就是备选的用来更新的内容，C^t 。在下一步，我们把这两部分联合起来，对 cell 的状态进行一个更新。

现在是更新旧细胞状态的时间了，Ct−1更新为Ct。前面的步骤已经决定了将会做什么，我们现在就是实际去完成。

我们把旧状态与ft相乘，丢弃掉我们确定需要丢弃的信息。接着加上it∗C\~t。这就是新的候选值，根据我们决定更新每个状态的程度进行变化。

输出门

最终，我们需要确定输出什么值。这个输出将会基于我们的细胞状态，但是也是一个过滤后的版本。首先，我们运行一个 sigmoid 层来确定细胞状态的哪个部分将输出出去。接着，我们把细胞状态通过 tanh 进行处理(得到一个在 -1 到 1 之间的值)并将它和 sigmoid 门的输出相乘，最终我们仅仅会输出我们确定输出的那部分。

实现

```

%%%% 基于粒子群算法优化lstm预测单序列 clc clear all close all %加载数据，重构为行向量 %加载数据，重构为行向量 data =xlsread('台风日数据2','Sheet1','B2:E481');%把你的负荷数据赋值给data变量就可以了。

%%

%序列的前 90% 用于训练，后 10% 用于测试 numTimeStepsTrain =round(0.8size(data,1)); dataTrain = data(1:numTimeStepsTrain,:)'; dataTest = data(numTimeStepsTrain+1:end-1,:)'; numTimeStepsTest = size(data,1)-numTimeStepsTrain-1 ;%步数 %% 数据归一化 [dataTrainStandardized, ps_input] = mapminmax(dataTrain,0,1); [dataTestStandardized, ps_output] = mapminmax(dataTest,0,1); %输入LSTM的时间序列交替一个时间步 XTrain = dataTrainStandardized(2:end,:); YTrain = dataTrainStandardized(1,:); [dataTrainStandardized_zong, ps_input_zong] = mapminmax(data',0,1); XTest_zong = dataTrainStandardized_zong(2:end,end);%测试集输入 YTest_zong = dataTest(1,1)';%测试集输出 XTest = dataTestStandardized(2:end,:);%测试集输入 YTest = dataTest(1,:)';%测试集输出 %% %创建LSTM回归网络，指定LSTM层的隐含单元个数963 %序列预测，因此，输入一维，输出一维 numFeatures = 3;%输入层数 numResponses = 1;%输出层数 numHiddenUnits = 20*3;

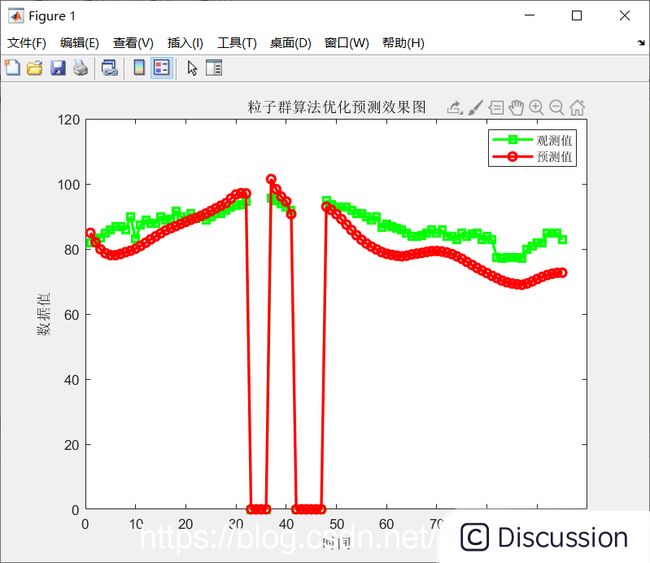
layers = [ ... sequenceInputLayer(numFeatures) lstmLayer(numHiddenUnits) fullyConnectedLayer(numResponses) regressionLayer]; %% 初始化种群 N = 5; % 初始种群个数 d = 1; % 空间维数 ger =100; % 最大迭代次数 limit = [0.001, 0.01;]; % 设置位置参数限制(矩阵的形式可以多维) vlimit = [-0.005, 0.005;]; % 设置速度限制 c1 = 0.8; % 惯性权重 c2 = 0.5; % 自我学习因子 c3 = 0.5; % 群体学习因子 for i = 1:d x(:,i) = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, 1);%初始种群的位置 end v = 0.005*rand(N, d); % 初始种群的速度 xm = x; % 每个个体的历史最佳位置 ym = zeros(1, d); % 种群的历史最佳位置 fxm = 1000*ones(N, 1); % 每个个体的历史最佳适应度 fym = 1000; % 种群历史最佳适应度 %% 粒子群工作 iter = 1; times = 1; record = zeros(ger, 1); % 记录器 while iter <= ger iter for i=1:N %指定训练选项，求解器设置为adam， 250 轮训练。 %梯度阈值设置为 1。指定初始学习率 0.005，在 125 轮训练后通过乘以因子 0.2 来降低学习 end disp(['最小值：',num2str(fym)]); disp(['变量取值：',num2str(ym)]); figure plot(record) title(['粒子群优化后Error-Cost曲线图，最佳学习率=',num2str(ym)]); xlabel('迭代次数') ylabel('误差适应度值') figure(2) % subplot(2,1,1) plot(YTest,'gs-','LineWidth',2) hold on plot(YPredbest,'ro-','LineWidth',2) hold off legend('观测值','预测值') xlabel('时间') ylabel('数据值') title('粒子群算法优化预测效果图') ```

​