强化学习笔记:DQN和DDQN
本文整理于datawhalechina.github.io的强化学习教程
0x01 intro
在 Q-learning 中,我们学习的是一个“评论函数” Q π ( s , a ) Q^\pi(s, a) Qπ(s,a),通过其函数值判断当前状态 s s s下采取动作 a a a好不好。
这个评论函数的输出值取决于agent的策略 π \pi π,即我们只能根据agent的具体策略才能判断他这个动作到底是好还是不好。
下面,为方便起见,我们将 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)简记为 Q ( s , a ) Q(s, a) Q(s,a)。
Q表只适用于状态值离散的情况和状态值不太大的情况。在 Q-learning 中,我们使用表格来存储每个状态 s s s下采取动作 a a a获得的奖励,即状态-动作值函数 Q ( s , a ) Q(s,a) Q(s,a)。然而,由于计算机内存的限制,这种方法无法用在状态量/动作量巨大甚至是连续的任务中。
此时,我们使用神经网络对Q函数做一个近似,即使用DQN。近似网络的输入输出有两种处理方法:
- 输入状态 s s s,输出是每一个动作的得分,即每一个动作的Q值。
- 输入状态 s s s和动作 a a a,输出Q值。
注意,以上我们假定策略 π \pi π是给定的,比如在每个状态 s s s下无脑选择Q值最大的 a a a。
0x02 MC和TD
MC
在初等概率论里,Monte-Calo方法通过进行大量重复实验,用频率近似概率来求解我们所需的概率分布。典型的例子是蒲丰投针问题。
在给定策略 π \pi π的情况下,我们为了估计 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a),可以这么做:
- 在状态 s s s,我们选取动作 a a a;
- 在动作 a a a执行完成之后,让agent根据 π \pi π来决定接下来怎么走,直到回合结束或者满足某些截止条件;
- 重复2多次,获得多个状态-动作序列,求出每一个序列每一步reward的折扣和,称为return,将这些return平均一下就可以作为 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)的估计;
- 用平均后的return和 s , a s, a s,a放到网络里做一做反向传播,训练网络;
- 对于0x01中所述的第一种网络而言,我们对每个 a a a都做一次1-4所述的采样,然后套个交叉熵,一块更新神经网络的值;对于第二种网络而言,只需要对指定的a做一次步骤1-4即可。
MC的做法有两个缺点。一个是采样得到的Q值方差很大,因为游戏的每一步都有不确定性,而且MC可能会走很多步才能结束,因此每一次采样的Q值可能很不相同;另一个是MC必须等到一个回合结束才可以开启下一个回合或者更新网络,太慢了。
TD
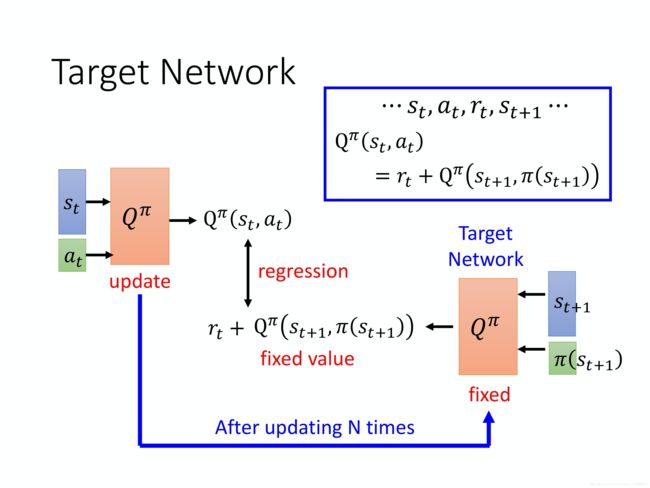
Temporal-Difference,又称时序差分。下图是DQN的原理图,我们将直接以此图为例来理解TD的过程。
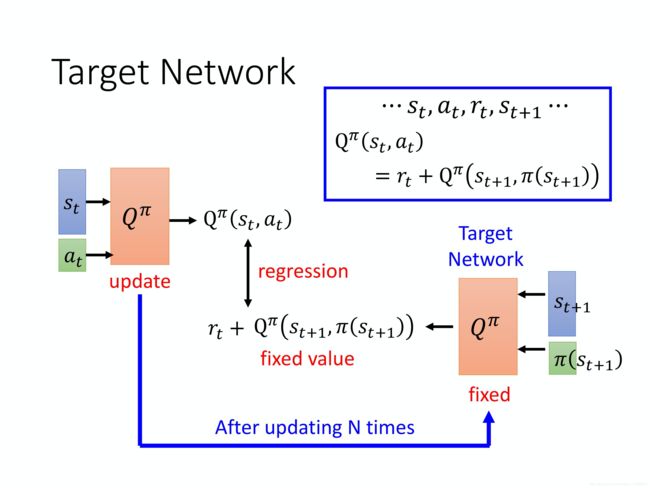
上图中,网络 Q π Q^\pi Qπ就是我们前面说的对Q值做近似的网络。我们以0x01中所说的第二种网络作说明。
在 t t t时刻,状态 s t s_t st,动作强制指定为 a t a_t at,输出(可能没训练好的)Q值 Q ( s t , a t ) Q(s_t, a_t) Q(st,at),然后状态跳到 s t + 1 s_{t+1} st+1。在 s t + 1 s_{t+1} st+1步,我们根据 π \pi π选择策略,获得Q值 Q ( s t + 1 , π ( s t + 1 ) ) Q(s_{t+1}, \pi(s_{t+1})) Q(st+1,π(st+1))。
此时,根据 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)的定义,
Q π ( s t , a t ) = r + γ Q π ( s t + 1 , π ( s t + 1 ) ) Q^\pi(s_t, a_t) = r + \gamma Q^\pi(s_{t+1}, \pi(s_{t+1})) Qπ(st,at)=r+γQπ(st+1,π(st+1))
于是我们想要 Q π ( s t , a t ) Q^\pi(s_t, a_t) Qπ(st,at)和 γ Q π ( s t + 1 , π ( s t + 1 ) ) \gamma Q^\pi(s_{t+1}, \pi(s_{t+1})) γQπ(st+1,π(st+1))差一个常数 r r r。
有了这个差值,按理说我们就可以作反向传播了。但是这两个网络都是没有训练好的,而且反向传播的话,怎么传播呢?
这个事会在0x04进行说明。
0x03 策略改进
这一部分,我们将说明,策略 π ( s ) = arg max a Q ( s , a ) \pi(s) = \argmax_a Q(s,a) π(s)=aargmaxQ(s,a),即每一步无脑选择Q值最大的a的策略,是永远的神。
它的大原则是这样,假设有一个初始的 π \pi π,也许一开始很烂,随机的也没有关系。这个 π \pi π 跟环境互动,会收集数据。接下来用TD或者MC学习一下 π \pi π 的 Q 值,即:学习一下 π \pi π 在某一个状态强制采取某一个动作、接下来用 π \pi π 这个策略会得到的期望奖励。学习了一下之后,策略 π ′ ( s ) = arg max a Q ( s , a ) \pi'(s) = \argmax_a Q(s,a) π′(s)=aargmaxQ(s,a)一定会比原来的策略 π \pi π还要好。
综上,假设你有一个 Q-function 和某一个策略 π \pi π,你根据策略 π \pi π学习出策略 π \pi π的 Q-function,接下来保证你可以找到一个新的策略 π ′ \pi' π′,它一定会比 π \pi π 还要好,然后你用 π ′ \pi' π′ 取代 π \pi π,再去找它的 Q-function,得到新的以后,再去找一个更好的策略。这样一直循环下去,策略就会越来越好。
什么叫好?我们定义在状态 s s s下回合开始,一直用 π \pi π作决策的期望回报return(reward的加权和)为 V π ( s ) V^\pi(s) Vπ(s)。于是, π \pi π 比 π ′ \pi' π′ “好”,指对任意的状态s, V π ( s ) ≥ V π ′ ( s ) V^\pi(s) \geq V^{\pi'}(s) Vπ(s)≥Vπ′(s)。
为什么用 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)和argmax搞出来的 π ′ \pi' π′就比原来的 π \pi π好呢?
由定义 V π ( s ) = Q π ( s , π ( s ) ) V^\pi(s) = Q^\pi(s, \pi(s)) Vπ(s)=Qπ(s,π(s))
Q π ( s , π ( s ) ) ≤ max a Q π ( s , a ) Q^\pi(s, \pi(s)) \leq \max_a Q^\pi(s,a) Qπ(s,π(s))≤amaxQπ(s,a)
但是 π ′ ( s ) = arg max a Q ( s , a ) \pi'(s) = \argmax_a Q(s,a) π′(s)=aargmaxQ(s,a),所以
V π ( s ) = Q π ( s , π ( s ) ) ≤ Q π ( s , π ′ ( s ) ) V^\pi(s) = Q^\pi(s, \pi(s)) \leq Q^\pi(s, \pi'(s)) Vπ(s)=Qπ(s,π(s))≤Qπ(s,π′(s))
这意味着,我变动当前一步的策略(在当前状态使用策略 π ′ \pi' π′,之后使用 π \pi π)的效果要比不变动的效果好。下面,我们将证明,我步步都使用 π ′ \pi' π′效果更好。
我懒得打字了,直接上图吧…
 总结一下,这一块内容告诉了我们每一步无脑选择最大Q值对应的动作a的合理性。
总结一下,这一块内容告诉了我们每一步无脑选择最大Q值对应的动作a的合理性。
0x04 DQN
0x02中我们说过这里讲一下怎么对TD做训练。
tip:Target Network
这里,我们会把图中标注了Target Network的那个网络固定住,然后使用反向传播更新左边的网络,等到左边的网络更新得差不多了(满足一定的条件)之后,再把左边网络的参数复制粘贴到右边的Target Network,然后再重复这个训练、粘贴的过程…
它们两个网络不要一起动,它们两个一起动的话,结果会很容易坏掉。
这里,左边的网络又叫Q-estimation网络,右面的叫Q-target网络。
tip:Exploration
假如我没有exploration,而是无脑选最大Q值对应的a的话,我们可以考虑这么一个例子:
我去一个餐厅吃饭,今天点了某一个东西以后,假如点了椒麻鸡,我觉得吼啊。那么接下来我每次去就都会点椒麻鸡,再也不会点别的东西了,那我就不知道别的东西是不是会比椒麻鸡好吃。
所以我们需要在里面引入随机因素,让模型看到更多的选择。
有两个方法解这个问题:
- 一个是 Epsilon Greedy:很大概率取Q值最大的那个选项,但是也存在瞎选的概率;
- 另一个是Boltzmann Exploration,这个方法就比较像是策略梯度。在策略梯度里面,网络的输出是一个期望的动作空间上面的一个的概率分布,再根据概率分布去做采样。那其实也可以根据 Q 值 去定一个概率分布,假设某一个动作的 Q 值越大,代表它越好,我们采取这个动作的机率就越高。但是某一个动作的 Q 值小,不代表我们不能尝试。
tip:Experience Replay
因为TD并不需要等到回合结束才能结算,可以每一步进行结算,所以我们可以保存每一步的信息。每一步的信息可以被放在buffer中,记录了(当前状态,当前动作,动作的奖励,下一个状态)。
有了这个 buffer 以后,我们会迭代地去训练这个 Q-function,在每次迭代里面,从 buffer 里面随机挑一个 batch 出来,和一般的网络一样去训练。
下面是DQN的原理示意图:
 注意,这里面,我们的策略 π \pi π始终是:无脑选择有最大Q值的动作。
注意,这里面,我们的策略 π \pi π始终是:无脑选择有最大Q值的动作。
0x05 DoubleDQN
我们的策略 π \pi π是无脑选择最大的策略。因为我们在更新Q网络的时候,总是会选择最大Q值的策略,因此,一旦有Q值被高估的情况出现,则我们总会选择被高估的Q值。
我们在DQN中,选择用target network来找Q值最大的a,并且用target network Q ′ Q' Q′来给出对应的Q值;但是在 Double DQN 里面,我们用更新参数的estimate network去选动作,然后拿target network(固定住不动的网络)去算值。
这么做的原因如下:
- 假设第一个 Q-function 高估了它现在选出来的动作 a,只要第二个 Q-function Q ′ Q' Q′没有高估这个动作 a 的值,那你算出来的就还是正常的值。
- 假设 Q ′ Q' Q′ 高估了某一个动作的值,那也没差,因为只要前面这个 Q 不要选那个动作出来就没事了
这个就是 Double DQN 神奇的地方。