深度学习修炼（五）——基于pytorch神经网络模型进行气温预测

5 基于pytorch神经网络模型进行气温预测

在前面的学习中，我们已经有了一个大概的思路，但是，线性模型毕竟十分简单，我们需要再搭建一个强化自己的知识点。

在这节课中，我们将会用到以下的数据集，请点击自主下载。

temps.zip - 气温预测数据集下载

感谢我吧！C站上面有那么多的付费资源，而我自掏腰包买了这个资源无偿分享。

5.1 实现前的知识补充

我们不同于前面的线性模型神经网络，我们在下面的小节中打算搭建的是一个多层感知机。

5.1.1 神经网络的表示

多层感知机是啥？让我们来看看线性回归的神经网络先。

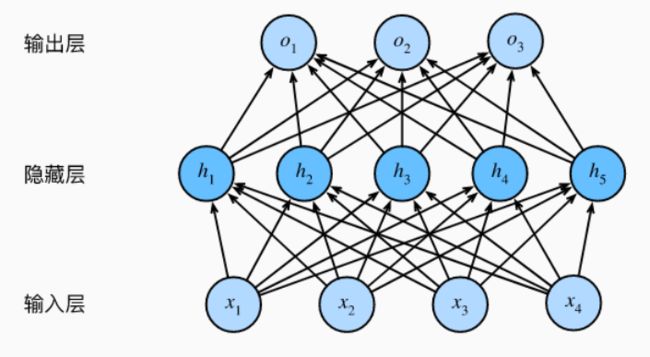
在之前的学习中，线性回归可以多参数，最终输出只有一个。但是在多层感知机中，它的模型架构确是这样：

以上的图是一个神经网络的图片，让我们给这个图片的不同部分取些名字。

我们由输入特征$x_1,x_2...x_n$，它们被竖直地堆叠起来，这叫做神经网络的输入层。但是前面我们也说过，这一层只提供输入特征，计算不在这一层，所以一般输入层是不算入神经网络的层数的。然后这里还有另外一层我们称之为隐藏层；而在最后一层是输出层，他负责产生预测值。

5.1.2 隐藏层

在训练集中，当通过神经网络的时候，隐藏层计算的值我们是不知道的，也就是说我们看不见它们在训练集中具有的值。当然你要是真想知道里面的值是啥，你可以从输入层开始根据隐藏层对应的算法一步一步算进去。

5.1.3 线性模型出错

虽然我们前面一直在用线性回归模型，但是并不代表我们能一直用下去。因为线性意味着自变量和因变量呈单调趋势。也就是说：特征变大模型输出就变大，特征变小输出就变小。

5.1.4 在网络中加入隐藏层

我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制， 使其能处理更普遍的函数关系类型。 要做到这一点，最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层，直到生成最后的输出。 我们可以把前L−1层看作表示，把最后一层看作线性预测器。 这种架构通常称为多层感知机(multilayer perceptron)，通常缩写为MLP。 下面，我们以图的方式描述了多层感知机。

5.1.5 激活函数

这里我们暂时不细讲激活函数，但是你需要知道的点是，在使用神经网络时，为了方式其输出单调，我们需要在隐藏层和输出层中使用激活函数，从而将输出结果投射到某个区间上。

激活函数有多种，如ReLU(修正线性单元)及其变体、sigmoid函数、tanh函数等。如果输出是0、1值（二分类问题），则输入层选择sigmoid函数，然后其它的所有单元都选择ReLU函数。这是很多激活函数的默认选择，如果在隐藏层上不确定用哪个激活函数，那么通常会使用ReLU激活函数。

5.1.6 小批量随机梯度下降

在前面机器学习中，我们曾经提到优化损失函数的方法是用梯度下降(gradient descent)的方法，这种方法几乎可以用来优化所有深度学习模型，他通过不断地在损失函数递减的方向上更新参数来降低误差。

梯度下降最简单的用法是计算损失函数关于模型参数的导数。但实际上执行可能会非常慢，因为每一次更新参数，我们基本遍历每个样本。一次，我们通常会在每次更新的时候抽取一小批样本，这种方法的变体我们叫做小批量随机梯度下降。如下面所示：

$(w,b)<-(w,b)-\frac{\eta }{|B|}{\sum }_{i\in B}{\partial }_{(w,b)}{l}^{(i)}(w,b)$

我们现在从所有的样本中抽取了$B$个样本，也就是小批量$B$。参数η我们叫做学习率。

5.2 实现的过程

5.2.1 预处理

在实现前，我们先导入所需的包。

import pandas as pd
import numpy as np
import torch
import matplotlib.pyplot as plt

我们把提前下载好的数据集加载进去，并且查看前五行以及特征，方便后续处理。

features = pd.read_csv('temps.csv')

# 查看数据前五行
features.head()

out：

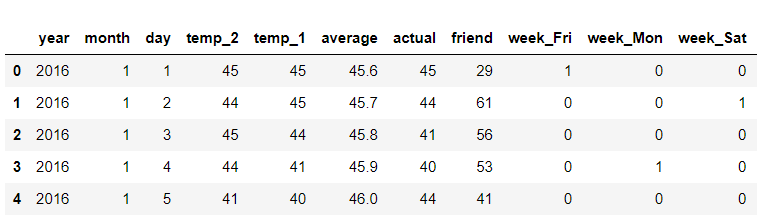
数据说明

• temp_2：前天的最高温度值
• temp_1：昨天的最高温度值
• average：在历史中，每年这一天的平均最高温度值
• actual：标签值，当天的真实最高温度
• friend：朋友预测的可能值

让我们查看数据有多少，即查看维度：

# 查看数据的维度
print('数据维度：',features.shape)

out：

数据维度： (348, 9)

我们注意到这里有很多关于时间的特征，我们将其处理为时间序列。如果你这里不是很懂，照做即可。

# 将时间转换为时间序列
import datetime

# 分别得到年、月、日
years = features['year']
months = features['month']
days = features['day']

# datetime格式
dates = [str(int(year))+'-'+str(int(month))+'-'+str(int(day)) for year,month,day in zip(years,months,days)]
dates = [datetime.datetime.strptime(date,'%Y-%m-%d') for date in dates]

打印结果看看！

dates[:5]

out：

[datetime.datetime(2016, 1, 1, 0, 0),
datetime.datetime(2016, 1, 2, 0, 0),
datetime.datetime(2016, 1, 3, 0, 0),
datetime.datetime(2016, 1, 4, 0, 0),
datetime.datetime(2016, 1, 5, 0, 0)]

除此之外，我们还注意到数据中的week特征为字符串，字符串可不能处理，我们必须将其转换为可处理的类型，根据前面所讲的知识点，我们将其转换为独热编码。

# 将week转为独热编码
features = pd.get_dummies(features)
features.head(5)

out：

我们是要预测当天的气温，所以我们应该把actual看做标签项，提取出来。

# 分离y_train
labels = np.array(features['actual'])

# 在特征中去掉y_train
features = features.drop('actual',axis = 1)

# 名字单独保存一下，以备后患
feature_list = list(features.columns)

# 转换成合适的格式
features = np.array(features)

查看一下训练集的大小：

features.shape

out：

(348, 14)

再次观察数据，有些特征的数据数值很大有些则很小，我们需要做标准化。从机器学习的学习得知，我们可以利用sklearn的库来进行标准化。

#有些数值大有些数值小，做标准化
from sklearn import preprocessing
input_features = preprocessing.StandardScaler().fit_transform(features)

5.2.2 搭建网络模型

首先我们需要将输出到网络模型中的数据转换为网络能接受的张量格式。

# 将array转为张量
x = torch.tensor(input_features,dtype = float)
y = torch.tensor(labels,dtype = float)

我们打算搭建具有一个隐藏层的多层感知机，为此，我们设定两个线性模型及参数，并且随机初始化它们。观察训练集的特征为14，所以输出层的w必须是(14,m)，其中m我随意指定为128，意为将14个输入特征转化为隐藏层的128个隐藏特征。由矩阵相乘知识可以得出的是348×128的矩阵，所以我们的biases指定为(128×1)。隐藏层同理。

# 权重参数初始化
weights = torch.randn((14,128),dtype = float,requires_grad = True)
biases = torch.randn(128,dtype = float,requires_grad = True)
weights2 = torch.randn((128,1),dtype = float,requires_grad = True)
biases2 = torch.randn(1,dtype = float,requires_grad = True)

我们还要指定学习率和存放每次计算所得损失的列表。

learning_rate = 0.001
losses = []

做完上述工作，我们开始对网络模型进行梯度下降。

# 指定梯度下降次数1000次
for i in range(1000):
    # 计算隐藏层-线性模型
    hidden = x.mm(weights) + biases
    # 加入激活函数-加入激活函数
    hidden = torch.relu(hidden)
    # 预测结果计算-输出值
    predictions = hidden.mm(weights2) + biases2
    # 计算损失-平方损失函数
    loss = torch.mean((predictions - y) ** 2)
    # 将每次的损失转为numpy格式并添加到损失列表中
    losses.append(loss.data.numpy())
    
    # 打印损失值
    if i % 100 == 0:
        print('loss:',loss)
    # 反向传播计算
    loss.backward()
    
    # 更新参数
    weights.data.add_(- learning_rate * weights.grad.data)
    biases.data.add_(- learning_rate * biases.grad.data)
    weights2.data.add_(- learning_rate * weights2.grad.data)
    biases2.data.add_(- learning_rate * biases2.grad.data)
    
    # 每次迭代后清空梯度
    weights.grad.data.zero_()
    biases.grad.data.zero_()
    weights2.grad.data.zero_()
    biases2.grad.data.zero_()

out：

loss: tensor(6845.0772, dtype=torch.float64, grad_fn=)
loss: tensor(155.3488, dtype=torch.float64, grad_fn=)
loss: tensor(147.4410, dtype=torch.float64, grad_fn=)
loss: tensor(145.0307, dtype=torch.float64, grad_fn=)
loss: tensor(143.6870, dtype=torch.float64, grad_fn=)
loss: tensor(142.8334, dtype=torch.float64, grad_fn=)
loss: tensor(142.2421, dtype=torch.float64, grad_fn=)
loss: tensor(141.7909, dtype=torch.float64, grad_fn=)
loss: tensor(141.4391, dtype=torch.float64, grad_fn=)
loss: tensor(141.1529, dtype=torch.float64, grad_fn=)

至此，训练模型完毕。以上就是一个简单的网络模型搭建过程。

5.3 简化实现

我们前面“基本上”是从零搭建了神经网络模型。而事实上，torch为我们提供了丰富的API帮我们实现神经网络，我们试着再一次实现。

# 指定规模
input_size = input_features.shape[1]
hidden_size = 128
output_size = 1
batch_size = 16

# 搭建网络
my_nn = torch.nn.Sequential(
    torch.nn.Linear(input_size,hidden_size),
    torch.nn.Sigmoid(),
    torch.nn.Linear(hidden_size,output_size),
)

# 定义损失函数
cost = torch.nn.MSELoss(reduction = 'mean')
optimizer = torch.optim.Adam(my_nn.parameters(),lr = 0.001)

# 训练网络
losses = []
for i in range(1000):
    batch_loss = []
    # 小批量随机梯度下降进行训练
    for start in range(0,len(input_features),batch_size):
        end = start+batch_size if start + batch_size < len(input_features) else len(input_features)
        xx = torch.tensor(input_features[start:end],dtype = torch.float,requires_grad = True)
        yy = torch.tensor(labels[start:end],dtype = torch.float,requires_grad = True)
        prediction = my_nn(xx)
        loss = cost(prediction,yy)
        optimizer.zero_grad()
        loss.backward(retain_graph=True)
        optimizer.step()
        batch_loss.append(loss.data.numpy())
        
    # 打印损失
    # 打印损失值
    if i % 100 == 0:
        losses.append(np.mean(batch_loss))
        print(i,np.mean(batch_loss))

out:

0 3984.4104
100 37.5414
200 35.608612
300 35.26231
400 35.09969
500 34.969772
600 34.853214
700 34.73715
800 34.61541
900 34.48683

5.4 评估模型

我们可以尝试用下面的代码去评估，代码较复杂，复制下去跑出看看效果即可。

x = torch.tensor(input_features,dtype = torch.float)
predict = my_nn(x).data.numpy()

# 转换日期格式
dates = [str(int(year))+'-'+str(int(month))+'-'+str(int(day)) for year,month,day in zip(years,months,days)]
dates = [datetime.datetime.strptime(date,'%Y-%m-%d') for date in dates]

# 创建一个表格来存日期和其对应的标签数值
true_data = pd.DataFrame(data = {'date':dates,'actual':labels})

# 同理，在创建一个来存日期和其对应的模型预测值
mouths = features[:,feature_list.index('month')]
days = features[:,feature_list.index('day')]
years = features[:,feature_list.index('year')]

test_dates = [str(int(year))+'-'+str(int(month))+'-'+str(int(day)) for year,month,day in zip(years,months,days)]
test_dates = [datetime.datetime.strptime(date,'%Y-%m-%d') for date in test_dates]

predictions_data = pd.DataFrame(data = {'date':test_dates,'prediction':predict.reshape(-1)})

# 真实值
plt.plot(true_data['date'],true_data['actual'],'b-',label = 'actual')

# 预测值
plt.plot(predictions_data['date'],predictions_data['prediction'],'ro',label = 'prediction')
plt.xticks(rotation = '60')
plt.legend()

# 图名
plt.xlabel('Date');plt.ylabel('Maximum Temperature (F)');plt.title('Actual and Predicted Values')

plt.show()

out：

看得出来，我们的模型拟合能力效果还是不错的。