论文阅读 || 目标检测系列——一文读懂YOLOv3

写在前面：
yolo3的了解，需要在yolo1和yolo2的基础上
yolo1：https://blog.csdn.net/magic_ll/article/details/105814514
yolo2：https://blog.csdn.net/magic_ll/article/details/106298494
.
yolo3的论文介绍的相对简单，主要还是需要阅读实现代码。自己阅读版本链接：https://github.com/YunYang1994/tensorflow-yolov3。 并重新训练了自己的数据，来更好的理解yolo3。
yolo3的解读，论文和实现工程以及其他博主的解读，然后根据自己的理解，完成了这篇yolo3的解析。
.

YOLO3的改进主要有：

• 调整了网络结构，并利用多尺度特征进行对象检测
• loss的优化

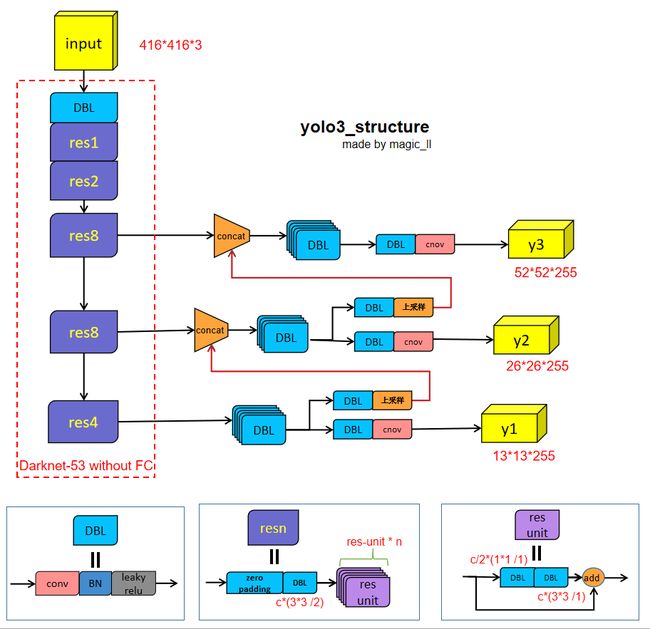
1 网络结构Darknet-53

图中结构模块：

• DBL：$conv+BN+leaky.relu$ 。构成了yolo3的结构中的最小组件，除最后一层卷积。（一般的，神经网络中都是如此，这里将relu更换为leaky-relu）
  注意 leaky ReLU 作为激活函数
• res-unit：这个模块是借鉴了ResNet的残差结构，可以让网络变得更深（yolo2中的darknet-19 -->> yolo3 中的darknet-53，前者没有残差结构）。
  $1.$ 残差结构中有一个直连通道，所以$input.shape=output.shape=(batch,h,w,c)$。
  $2.$ 第一层卷积为 $c/2\ast (1\ast 1/1)$
  $3.$ 第二层卷积为 $c\ast (3\ast 3/1)$
• resn：n代表数字，代表着含有n个res-unit模块。yolo3结构中有res1,res2,res4,res8。每一个resn会带来feature map的降维1/2，模块中的第一个卷积为：$c\ast (3\ast 3/2)$，与zeropadding一起完成特征图的降维。
• concat：注意与add的区别。
  add：来源于ResNet思想，让卷积学习输入与输出的差量，即$y=f(x)+x$
  concat：来源于DenseNet网络的设计思路，将特征图按照通道维度直接进行拼接
• 上采样：将小尺寸特征图通过插值（近邻插值算法等）等方法，得到大尺寸的图像。不改变通道数

.
网络设计思想：

• yolo3借鉴了金字塔特征图思想（FPN论文中）：小尺寸特征用于检测大尺寸物体，大尺寸特征图检测小尺寸物体。
  yolo3总共输出了3个特征图，三个特征图分别下采样倍数$32,16,8$。网络会将特征图“倍数32”，上采样尺寸到16和特征图“倍数16”，进行concat；再将特征图“倍数16”上采样尺寸到8 和特征图“倍数8”进行concat。
• 每个特征图的输出围度为$N\ast N\ast [3\ast (4+1+80)]$。其中$N\ast N$为输出特征图的grid数量；3为一个grid有3个anchor box；每个box有4维预测框位置$t_x,t_y,t_w,t_h$，1维预测框的$confidence$，80维物体的$classes$。所以输出为$N\ast N\ast 255$。

2 yolo3输出特征图解码

2.1 yolo3的label

以输入尺寸 416x416x3 为例，此时的网络的输出尺寸为13x13, 26x26, 52x52。

• 先验框的设定
  与yolo2一样，使用$K-means$聚类得到先验框的尺寸。每个尺寸的输出设定3个先验框，一共9个。在COCO数据集上（原始图片全部resize为416 × 416），9个先验框为：(10x13),(16x30),(33x23),(30x61),(62x45),(59x199),(116x90),(156x198),(373x326)。

  • 遵循“大尺寸预测小物体，小尺寸预测大物体”的原则，
    13*13的特征图有较大感受野，对应的先验框(116x90),(156x198),(373x326)
    26*26的特征图有中等感受野，对应的先验框(30x61),(62x45),(59x199)
    52*52的特征图有较小感受野，对应的先验框(10x13),(16x30),(33x23)
    注意：先验框只与检验框的w,、h有关，与x、y无关

• 置信度的设定
  方式1：yolo1 & yolo2中，$confidenc{e}_{box}=1_{是否存在物体}\ast IO{U}_{pred}^{true}$

  • 该方式置信度的标签会始终很小，无法有效的学习，检测时召回率不高。例：在训练过程中，某些$\ast IO{U}_{pred}^{true}$的极限为0.8，然后以0.8作为标签训练，神经网络学习的结果为0.6，这时候设置阈值0.7，就会把正确的框丢弃了。尤其在小物体的与测试，几个像素值就很大程度上影响着IOU。

  方式2：yolo3中，$confidenc{e}_{box}=1_{是否存在物体}$，也就是非0即1。

.

2.2 网络输出的解码

前面说过，每个特征图的输出围度为$N\ast N\ast 3\ast (4+1+80)$。其中$N\ast N$为输出特征图的grid数量；3为一个grid有3个anchor box；每个box有4维预测框位置$t_x,t_y,t_w,t_h$，1维预测框的$confidence$，80维物体的$classes$。

• 检测框解码
  获取到了网络的输出以及先验框后，解码检测框$x,y,w,h$：$$b_x=\sigma (t_x)+c_x$$ $$b_y=\sigma (t_y)+c_y$$ $$b_w=p_w{e}^{t_w}$$ $$b_h=p_h{e}^{t_n}$$其中：$t_x,t_y,t_w,t_h$为网络输出的部分内容；$\sigma (t_x),\sigma (t_y)$是基于矩形框中心点左上角格点坐标的偏移量；$p_w,p_h$是先验框的宽高。这组公式在yolo2中有详细介绍。得到的$b_x,b_y,b_w,b_h$为预测框的中心和宽高（归一化后的）。

• 置信度的解码
  置信度在输出的85维中占一位，由sigmoid函数计算即可，数值在[0,1]之间。

• 类别解码
  COCO数据集由80类，在85维占了80维。使用sigmoid代替了Yolo2中的softmax，每一维独立代表一个类别的置信度，取消了类别之间的互斥，使网络更加灵活

  .
  对网络预测的output特征进行解码，就可以得到预测框的信息

3 损失函数相关设定

3.1 三种预测框

当输入尺寸为320x320时，可得到$(8^2+16^2+32^2)\ast 3=4032$个先验框
预测框一共分为三种情况：正样本、负样本、忽略样本

• 正样本：
  定义：假设图片中有2个物体的真实框：1. 第一个真实框与4032个先验框计算IOU，最大的先验框为正样本（一个真实框只分配一个先验框）。2. 第二个真实框在4031个先验框中，得到IOU最大的先验框为正样本。 真实框的先后顺序可以忽略。如果该最大IOU小于阈值（论文中0.5），也为正样本。
  标签：正样本的检测框loss的标签为ground truth box的$(x,y,w,h)$编码后的$(t_x,t_y,t_w,t_h)$、
  类别loss的标签为类别数的one-hot形式。置信度loss的标签为1。
• 忽略样本
  正样本除外，与任意一个真实框的IOU大于阈值的预测框，为忽略样本，不产生任何loss。
• 负样本
  正样本除外，与真实框的IOU小于阈值的预测框，为负样本。只产生置信度loss，标签为0。

---

其实自己在阅读yolo2的时候，就存在疑惑：为什么要有忽略样本的存在，为什么不把正样本以外的预测框全部归为负样本。然后自己强行分析一波
分析：

• 将COCO中的9个先验框的大小画出，如下图。我们可以看到不同先验框之间存在重合检测部分。
  如果有一个物体，训练时在“32倍降采样”的特征图中的第三个box，IOU达0.9；在“16倍降采样”的特征图中的第一个box，IOU达0.89。这种情况，IOU为0.89的box学习到的特征，明显与IOU为0.9的box“距离更近”，与IOU小于0.5的box“距离“更远，此时如果将IOU为0.89的框置信度赋为0的标签，与其他IOU小于0.5的box归为同一种情况，网络学习效果便会不理想

.
实验：随后补充

3.2 loss的公式

$$loss=los{s}_{n1}+los{s}_{n2}+los{s}_{n3}$$ $$los{s}_{n1}={\lambda }_{noobj}\sum _{i=0}^{N_1\ast N_1}\sum _{j=0}^3\ast 1_{ij}^{noobj}\ast log(1-c_{ij})$$ $$+{\lambda }_{obj}\sum _{i=0}^{N_1\ast N_1}\sum _{j=0}^3\ast 1_{ij}^{obj}\ast log(c_{ij})$$ $$+{\lambda }_{box}\sum _{i=0}^{N_1\ast N_1}\sum _{j=0}^3\ast 1_{ij}^{obj}\ast [(t_x-t_x^{{}^{\prime }}{)}^2+(t_y-t_y^{{}^{\prime }}{)}^2]$$ $$+{\lambda }_{box}\sum _{i=0}^{N_1\ast N_1}\sum _{j=0}^3\ast 1_{ij}^{obj}\ast [(t_w-t_w^{{}^{\prime }}{)}^2+(t_h-t_h^{{}^{\prime }}{)}^2]$$ $$+{\lambda }_{class}\sum _{i=0}^{N_1\ast N_1}\sum _{j=0}^3\ast 1_{ij}^{obj}\ast [p_{ij}^{{}^{\prime }}(c)\ast log(p_{ij}c)+(1-p_{ij}^{{}^{\prime }}(c))\ast log(1-p_{ij}(c))]$$其中$los{s}_{n1}$的计算中

• 第一行：负样本的置信度的loss计算。第二行：正样本的置信度的loss计算。第三四行：正样本的xywh的loss计算。第五行：正样本的的分类loss
• $\lambda$：权重系数，控制各loss之间的比例。通常正样本的数量很小于负样本，所以需要系数来调控
• $1_{ij}^{obj}$若是正样本则为1，否则为0；$1_{ij}^{noobj}$若是负样本则为1，否则为0；忽略样本就都为0
• $(x,y,w,h)$的损失使用的是均方差，也可以使用Faster R-CNN中的 smooth L1 损失。smooth L1使训练更平滑。
  $(confidense,class)$使用的标签是0,1构成的标签，使用的是交叉熵作为损失函数。

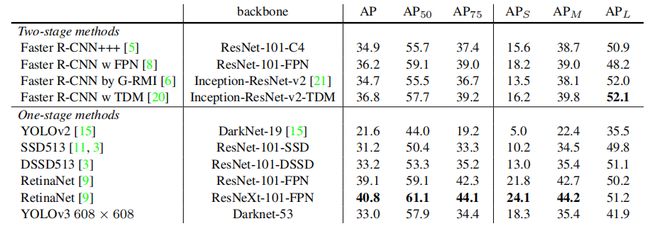
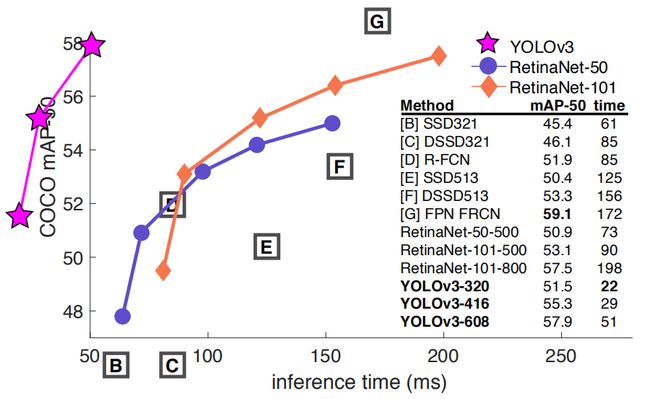
4 实验结果对比

速度上，yolov3最快，比效果最好的模型RetinaNet速度快3倍。
精度上，yolov3逊色于RetinaNet，略低于Faster RCNN，略优于SSD。
当我们关注 $mA{P}_{50}$ 时，yolov3更是在时间上和精度上达到了一个很佳的平衡。

5 无效的尝试

• anchor box 坐标的偏移预测：
  作者尝试了常规的预测方法，如使用线性激活来将 $x,y$ 的偏移 预测为边界框宽度或高度的倍数，这种操作降低了模型的稳定性且效果不佳
• 用线性激活（Linear）预测$(x,y)$
  而不是逻辑激活（logistic）。效果不佳
• 双 IOU 阈值和样本分配：
  训练时，Faster RCNN 使用了两个iou阈值。计算预测框和真实框的iou，(0.7,1]为正样本，[0.3,0.7]为忽略样本，[0,0.3)为负样本。yolov3尝试这种方式，效果并不好。待我得空复习下FasterRCNN，再来强行分析。

9个anchorbox的图的实现代码（随便记录下）：

import cv2
import numpy as np

image = np.zeros((416,416,3))

anchor_box = [(10, 13), (16, 30), (33, 23), (30, 61), (62, 45), (59, 199), (116, 90), (156, 198), (373, 326)]
anchor_box = anchor_box[::-1]

for i in range(0,9):
    center = [416/2, 416/2]
    x = int(center[0]-anchor_box[i][0]/2)
    y = int(center[1]-anchor_box[i][1]/2)
    m = int(center[0]+anchor_box[i][0]/2)
    n = int(center[1]+anchor_box[i][1]/2)
    cv2.rectangle(image, (x, y), (m, n), (0, 0, 255), 3) if(i in [0,1,2]) else print()
    cv2.rectangle(image, (x, y), (m, n), (0, 255, 0), 2) if(i in [3,4,5]) else print()
    cv2.rectangle(image, (x, y), (m, n), (255, 0, 255), 1) if(i in [6,7,8]) else print()

cv2.namedWindow("test", 0)
cv2.resizeWindow("test",416,416)
cv2.imshow("test",image)
cv2.waitKey(0)
cv2.destroyAllWindows()