智能优化算法:多元宇宙优化算法-附代码
智能优化算法:多元宇宙优化算法-附代码
文章目录
- 智能优化算法:多元宇宙优化算法-附代码
-
- 1.算法原理
- 2.算法流程图
- 3.算法结果
- 4.参考文献
- 5.MATLAB代码
- 6.python代码
摘要:多元宇宙优化算法(Multi-Verse Optimizer,MVO)是Seyedali Mirjalili等于2016年提出的一种新型智能优化算法[1]。它基于宇宙中的物质通过虫洞由白洞向黑洞进行转移的原理进行模拟。在MVO算法中,主要的性能参数是虫洞存在概率和虫洞旅行距离率,参数相对较少,低维度数值实验表现出了相对较优异的性能。
1.算法原理
该算法主要借助宇宙在随机创建过程中高膨胀率物体总是趋于低膨胀率的物体,这种万有引力作用可以使物体转移,借助相关宇宙学规则,可以在搜索空间逐渐趋于最优位置.遍历过程主要分为探索和开采过程,虫洞可以作为转移物体的媒介,通过白洞和黑洞交互作用进行搜索空间探测,本文算法具体操作如下:
假设搜索空间存在宇宙矩阵为:
U = [ x 1 1 , x 1 2 , . . . , x 1 d x 2 1 , x 2 2 , . . . , x 2 d . . . . . . x n n , x n 2 , . . . , x n d ] (1) U=\left[ \begin{matrix} x_{1}^{1},x_{1}^{2},...,x_{1}^{d}\\ x_{2}^{1},x_{2}^{2},...,x_{2}^{d}\\ ......\\ x_{n}^{n},x_{n}^{2},...,x_{n}^{d} \end{matrix}\right]\tag{1} U=⎣⎢⎢⎡x11,x12,...,x1dx21,x22,...,x2d......xnn,xn2,...,xnd⎦⎥⎥⎤(1)
式中: d d d 为变量个数; n n n 为宇宙数量(候选解);
x i j = { x k j r 1 < N I ( U i ) x i j r 1 ≥ N l ( U i ) (2) x_{i}^{j}=\begin{cases} x_{k}^{j} \quad r_{1}
式中: x i j x_{i}^{j} xij为第 i i i个宇宙的第 j j j个变量; U i U_{i} Ui为第 i i i个宇宙; N I ( U i ) NI(U_{i}) NI(Ui)为第 i i i个宇宙的标准膨胀率; r 1 r_{1} r1为介于0 和1的随机数; x k j x_{k}^{j} xkj为根据螺旋机制被选中的第 i i i 个宇宙的第 j j j个变量。
通过式(2)依据标准膨胀率大小,白洞将以螺旋形式搜索,膨胀率低的物体更易于通过白洞或黑洞输送物体. 同等情况下,膨胀率更高的物体具有更强拥有白洞的可能性,膨胀率更低的物体拥有黑洞的可能性更低. 对于最大化问题, − N I -NI −NI将被改变为 N I NI NI。 根据搜索机制,在排除扰动影响时,为了使其始终处于探索过程,每个宇宙将物体通过虫洞随机传送. 白洞传送物体穿过虫洞,如图 1 所示.
为了提高宇宙利用虫洞提高物体膨胀率的可能性,假设虫洞隧道总是建立在宇宙和最优宇宙之间.这种机制可以公式为:
x i j = { { X j + T D R ∗ ( ( u b j − l b j ) ∗ r 4 + l b j ) r 3 < 0.5 X j − T D R ∗ ( ( u b j − l b j ) ∗ r 4 + l b j ) r 3 ≥ 0.5 x i j r 2 ≥ W E P (3) x_{i}^{j}=\begin{cases} \begin{cases} Xj + TDR*((ub_{j}-lb_{j})*r_{4}+lb_{j}) \quad r_{3}<0.5\\ Xj-TDR*((ub_{j}-lb_{j})*r_{4}+lb_{j}) \quad r_{3}\geq 0.5 \end{cases}\\ x_{i}^{j} \quad r_{2} \geq WEP \end{cases} \tag{3} xij=⎩⎪⎨⎪⎧{Xj+TDR∗((ubj−lbj)∗r4+lbj)r3<0.5Xj−TDR∗((ubj−lbj)∗r4+lbj)r3≥0.5xijr2≥WEP(3)
式中: X j X_{j} Xj为目前最优宇宙的第 j j j 个变量, W E P WEP WEP 和 T D R TDR TDR 是两个系数; u b j ub_{j} ubj 为第 j j j 个变量最高值; l b j lb_{j} lbj 为第 j j j 个变量最低值; x j i x_{j}^{i} xji 为第 i 个宇宙的第 j j j 个变量; r 2 , r 3 , r 4 r_{2} ,r_{3} ,r_{4} r2,r3,r4 均为介于 0 和 1 的随机数。
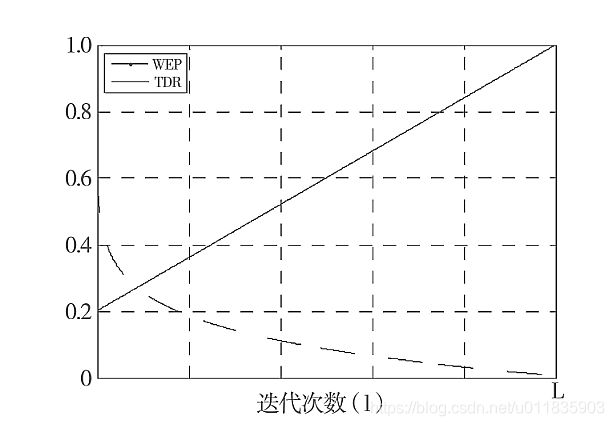
这种机制主要存在两个系数:虫洞存在可能性(Wormhole Existence Probability,WEP) 和旅程距离速率(Travelling DistanceRate,TDR),TDR 系数用于定义宇宙空间虫洞存在可能性,同时表示物体在最优宇宙附近通过虫洞进行转换的距离。
W E P = m i n + l ∗ ( m a x − m i n L ) (4) WEP = min +l*(\frac{max-min}{L})\tag{4} WEP=min+l∗(Lmax−min)(4)
式中: m i n min min 为 W E P WEP WEP 最小值; m a x max max 为 W E P WEP WEP 最大值; l l l 为当前迭代次数; L L L为最大迭代次数。
T D R = 1 − l 1 / p L 1 / p (5) TDR = 1 - \frac{l^{1/p}}{L^{1/p}}\tag{5} TDR=1−L1/pl1/p(5)
式中: p p p 定义了随迭代次数改变的探测速度, p p p 值越高,局部探测速度越快,用时越短. 两个参数随时间变化曲线图,如图 2 所示.
2.算法流程图
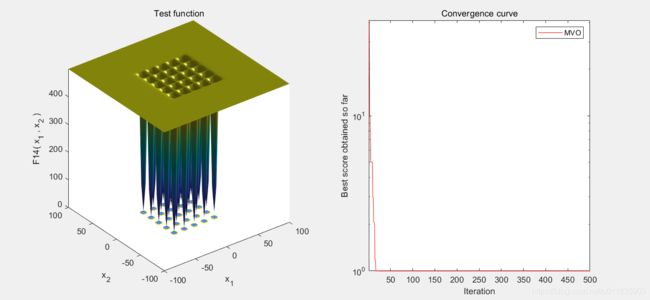
3.算法结果
4.参考文献
[1]Mirjalili S, Mirjalili S M, Hatamlou A, et al. Multi-Verse Optimizer: a nature-inspired algorithm for global optimization[J]. Neural Computing and Applications, 2016, 27(2): 495-513.
[2]刘世宇,王孜航,杨德友.多元宇宙算法及其在电力系统环境经济调度的应用[J].东北电力大学学报,2018,38(04):19-26.
5.MATLAB代码
多元宇宙算法
算法相关应用
| 名称 | 说明或者参考文献 |
|---|---|
| 基于多元宇宙算法的无线传感器网(WSN)覆盖优化 | https://blog.csdn.net/u011835903/article/details/109262039 (原理一样,只是优化算法是多元宇宙算法) |
| 基于多元宇宙算法的3D无线传感器网(WSN)覆盖优化 | https://blog.csdn.net/u011835903/article/details/113834323(原理一样,只是优化算法是多元宇宙算法) |
6.python代码
个人资料介绍