python代码实现bp神经网络（反向传播）

前向传播过程的向量化表示，以及所有公式对应维度如下：

反向传播过程的向量化表示如下，所有符号维度和前向传播的一致：

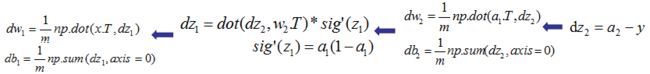
实现一个3层神经元，输入层4个神经元，隐藏层3个神经元，输出层2个神经元的代码如下：

import numpy as np

def parameter_initializer(n1, n2, n3):
    """ 初始化权值 """
    w1 = np.random.normal(scale=(2.0/n1)**0.5, size=(n1, n2))
    b1 = np.zeros(shape=(1,n2))
    w2 = np.random.normal(scale=(2.0/n2)**0.5, size=(n2, n3))
    b2 = np.zeros(shape=(1, n3))
    return w1, b1, w2, b2

def sigmoid(z):
    a = 1/(1+np.exp(-z))
    return a

def forward_propagate(x, w1, b1, w2, b2):
    """ 构建三层神经网络 -- 前向传播 """
    """ x.shape = (m,n1)
        y.shape = (m, n3)
        w1.shape = (n, n2)
        b1.shape = (1, n2)
        w2.shape = (n2, n3)
        b2.shape = (1, n3)
    """
    z_1 = np.dot(x, w1) + b1
    a_1 = sigmoid(z_1)
    z_2 = np.dot(a_1, w2) + b2
    output = sigmoid(z_2)
    return a_1, output

def loss(output, y):
    """ 损失函数 """
    cross_entropy = -((1-y)*np.log(1-output) + y * np.log(output))
    cost = np.mean(np.sum(cross_entropy, axis=1))
    return cost

def back_propagate(w1,b1, w2, b2, a_1, output, y, learning_rate):
    """ 反向传播 """
    m = y.shape[0]
    dz_2 = output - y    # (m, n3)
    dw2 = 1/m * np.dot(a_1.T, dz_2)  # (n2, n3)
    db2 = 1/m * np.sum(dz_2, axis=0, keepdims=True)

    # 梯度下降
    w2 = w2 - learning_rate * dw2
    b2 = b2 - learning_rate * db2

    dz_1 = np.dot(dz_2, w2.T) * ((1-a_1)*a_1)  # sigmoid(z_1)的导数  # (m, n2)
    dw1 = 1/m * np.dot(x.T, dz_1)  # (n1, n2)
    db1 = 1/m * np.sum(dz_1, axis=0, keepdims=True)  # (1, n2)

    w1 = w1 - learning_rate * dw1
    b1 = b1 - learning_rate * db1

    return w1, b1, w2, b2

def bpnn(x, y, epochs, learning_rate):
    w1,b1,w2,b2 = parameter_initializer(4,3,2)
    for epoch in range(epochs):
        a_1, output = forward_propagate(x, w1, b1, w2, b2)
        cost = loss(output, y)
        print("{} epoch, cost is {}".format(epoch, cost))
        w1, b1, w2, b2 = back_propagate(w1, b1, w2, b2, a_1, output, y, learning_rate)
    return w1,b1,w2,b2


if __name__ == "__main__":

    x = np.arange(0,20).reshape(5,4)
    y = np.array([[1,0],[1,0],[0,1],[0,1],[0,1]], dtype=float).reshape(5,2)

    w1, b1, w2, b2 = bpnn(x, y, 100, 0.1)
    print(w1, b1, w2, b2)

    # 测试效果
    x_test = np.array([[1,3,2,4], [4,5,7,4], [7,9,12,7]])
    output = forward_propagate(x_test, w1, b1, w2, b2)

    print(output)