1下-21-5月-2

—–gets()与puts()和cin>>与cout<<的比较(7.21)—–

#include
#include
#include
using namespace std;
int main()
{
    char a[100], b[100];
    cout<<"输入一个字符串（gets方式）：";
    gets (a);
    puts (a);

    cout<<"输入一个字符串（cin方式）：";
    cin>>b;
    cout<<b;

    cout<<endl;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//总结： 
// 1.gets()能够接收含有空格的字符串，而cin>> 只能接受空格前边的一段字符！ 
// 2.puts()能够输出含有空格是字符串，而cout<< 只能输出空格前边的一段字符！ 
// 3.puts()只能用于输出字符串！ 
// 4.当要输入的字符串本身含有空格时，要用gets()不用cin>>!

原文链接：https://blog.csdn.net/qq_29486343/article/details/46993567

/*18931 分形
时间限制:1000MS  代码长度限制:10KB
提交次数:0 通过次数:0
题型: 编程题   语言: 不限定
Description
分形，具有以非整数维形式充填空间的形态特征。
通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”，即具有自相似的性质。
现在，定义“盒子分形”如下：
一级盒子分形：
   X
二级盒子分形：
   X X
	X
   X X
如果用B(n - 1)代表第n-1级盒子分形，那么第n级盒子分形即为：
  B(n - 1)        B(n - 1)
		  B(n - 1)
  B(n - 1)        B(n - 1)
你的任务是绘制一个n级的盒子分形。
输入格式
输入一个不大于6的正整数n，代表要输出的盒子分形的等级。
输出格式
使用“X”符号输出对应等级的盒子分形。
输入样例
4
输出样例
		123456789                 27
1       X X   X X         X X   X X
2        X     X           X     X
3       X X   X X         X X   X X
		   X X               X X
			X                 X
		   X X               X X
		X X   X X         X X   X X
		 X     X           X     X
9       X X   X X         X X   X X
				 X X   X X
				  X     X
				 X X   X X
					X X
					 X
					X X
				 X X   X X
				  X     X
				 X X   X X
		X X   X X         X X   X X
		 X     X           X     X
		X X   X X         X X   X X
		   X X               X X
			X                 X
		   X X               X X
		X X   X X         X X   X X
		 X     X           X     X
27      X X   X X         X X   X X
https://blog.csdn.net/qq_21472271/article/details/111622638
*/
 
#include
#include
char w[30][30];
void dfs(int n, int x, int y)
{
	if (n == 1)
	{
		w[x][y] = 'X';
		return;
	}//递归终止条件 当图形规模小成一个X就可以输入了
	int m = pow(3, n - 2);//表示 3的n-2次方 算出的是一个图案的高或者宽（其实就是图案大小）
    //下面这些可以随意调换顺序
	dfs(n - 1, x, y);//查找左上
	dfs(n - 1, x + m, y + m);//查找中间 左上角到中间 行和列要加上图案的大小
	dfs(n - 1, x + 2 * m, y);//查找左下 左上角到左下 行要加上2倍图案的大小
	dfs(n - 1, x, y + 2 * m);//查找左上 左上角到左上 列要加上2倍图案的大小
	dfs(n - 1, x + 2 * m, y + 2 * m);//查找右下 左上角到右上 行和列要加上2倍图案的大小
}
int main()
{
	int n;
	scanf("%d", &n);
	int k = pow(3, n - 1);// 算行和列大小
	for (int i = 0; i < k; i++)
		for (int j = 0; j < k; j++)
			w[i][j] = ' ';  //表格初始化
	for (int i = 0; i < k; i++)
		w[i][k] = '\0';//加上换行符号
	dfs(n, 0, 0);//给表格填X 起点为0,0 以左上角为起点
	for (int i = 0; i < k; i++)
		puts(w[i]);//输出答案
}
 

void strlower (char *a) {//手写函数，将大写字母转换成小写字母
	for(int i = 0; a[i]; i ++ ) {
		if(isupper(a[i])) a[i] = tolower(a[i]);//isupper是判断是否是大写字母的系统函数，tolower是将其转换成小写字母的函数
	}
}

这道题其实可以用map来做，map就是映射，在这里可以把一个字符映射成一个数，就是要按几次才能按出这个数

其实map的功能很强大，这里只用了他的基本性质

代码~

#include
#include
#include
#include 
#include
using namespace std;
map<char,int>ma;//定义map，把char类型转化成int
string word;
int ans=0;
void init()
{
    ma['a']=1;
    ma['b']=2;
    ma['c']=3;
    ma['d']=1;
    ma['e']=2;
    ma['f']=3;
    ma['g']=1;
    ma['h']=2;
    ma['i']=3;
    ma['j']=1;
    ma['k']=2;
    ma['l']=3;
    ma['m']=1;
    ma['n']=2;
    ma['o']=3;
    ma['p']=1;
    ma['q']=2;
    ma['r']=3;
    ma['s']=4;
    ma['t']=1;
    ma['u']=2;
    ma['v']=3;
    ma['w']=1;
    ma['x']=2;
    ma['y']=3;
    ma['z']=4;
    ma[' ']=1;
}//初始化

int main()
{
    init();
    getline(cin,word);//读入
    for(int i=0;i<word.length();i++)
    {
        ans+=ma[word[i]];
    }
    cout<<ans<<endl;
}

//https://www.luogu.com.cn/problem/solution/P1765

//
3、使用map

使用map得包含map类所在的头文件 

#include  //注意，STL头文件没有扩展名.h 

map对象是模板类，需要关键字和存储对象两个模板参数：

std:map<int, string> personnel; 

这样就定义了一个用int作为索引,并拥有相关联的指向string的指针. 



1. map最基本的构造函数：

map<string, int>  mapstring;
map<int, string> mapint;
map<string, char> mapstring;
map<char, string> mapchar;
map<char, int> mapchar;
map<int, char> mapint;
 

2. map添加数据:

map<int ,string> mapname;  
 
mapname.insert(pair<int, string>(102,"liao"));
 
mapname.insert(map<int,string>::value_type(321,"xiaona"));
 
mapname[112] = "hahaha";//map中最简单最常用的插入添加

直接按照题目意思，利用字符操作列表达式输出即可。

代码如下：

#include 
int main()
{
    char in[100]; 
    int n, j; 
    scanf("%d%s", &n, in); //读入 
    for(j = 0; in[j] != '\0'; j++)
        putchar((in[j]-'a'+n)%26+'a'); 
    //in[j]-'a':读入中对应的第几个字母的位置，比如'a'对应0，'b'对应1，'c'对应2（0开始）；
    //in[j]-'a'+n:读入中对应字母加上转移位数得到的字母的对应位置。
    //比如说'c'这个字母移动3位，就是第2个字母向右移动3个，就是第五个字母，即'f'
    //取余26是防止移动位数超过26导致炸掉
    //再加上'a'，将对应位置还原成字母，再打出来 
}

n&(1<<i)的含义

feiyu_diary 2017-12-14 15:20:17   3796   收藏 14
版权
1<<i 是将1左移i位，即第i位为1，其余位为0；

例如1<<2 则0001->0100

n&(1<<i)是将左移i位的1与n进行按位与，即为保留n的第i位，其余位置零

如果n第i位为0，则n&(1<<i)的值为0

否则不为0

常用if(n&(1<<i)==0)用于判断n的第i位是否为0

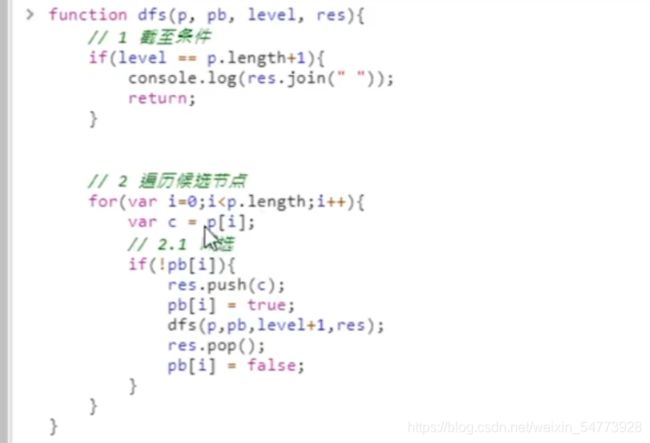
Description
把 1至n 这 n 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式
一个整数n。(1<=n<=9)

输出格式
按照从小到大的顺序输出所有方案，每行一个方案。
同一行相邻两个数用一个空格隔开。
对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

输入样例
3

输出样例
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

#include 

using namespace std;
int ans[105],vis[105],n;/*实现N个数的全排列，vis是标记数组，
                        ans记录一次从根结点到叶结点选过的所有数字*/
void dfs(int step)

{
    if(step==n+1)//这一次将不取数，直接按顺序输出这一条线下取过的数
    {
        for(int i=1; i<=n; i++)
            cout<<ans[i]<<' ';
        cout<<endl;
        return;
    }
    for(int i=1; i<=n; i++)/*该次for循环代表同一个根结点下同一层
    所有数,通过i++来实现在同一层中切换子结点
        */
        if(vis[i]==0)//判断是不是同一条线取过的数
        {

            ans[step]=i;//将这次取的数记录下来
            vis[i]=1;//取过的数打上标记
            dfs(step+1);//向下取同一条线上取过的数
            vis[i]=0;/*这一条线全部取完后，递归会依次结束，
                结束一次递归就将对应的标记清除一次，
                以此实现清除 除根结点外的所有标记*/
        }
}

int main()
{
    cin>>n;
    dfs(1);//这将是我第一次取数(step)
    return 0;
}


回溯法，标记了当前的节点，顺便本题
当前节点又是不用的，刚好。

三个要求！！！

#include 
#include 

using namespace std;

int n,rep[15];

void dfs(int rest,int k)
{
    if(rest==0)//exit
    {
        printf("%d=",n);
        for(int i=0;i<k-1;i++)
        {
            printf("%d+",rep[i]);
        }
        printf("%d\n",rep[k-1]);
        return ;
    }
    for(int i=rest;i>=1;i--)
    {
        if(k==0)
        {
            rep[k]=i;
            dfs(rest-i,k+1);
        }
        else if(i<=rep[k-1])
        {
            rep[k]=i;
            dfs(rest-i,k+1);
        }
    }
    return ;
}

int main()
{
    scanf("%d",&n);
    dfs(n,0);
    return 0;
}

很明显，k是第几层的数，a[k]是第k层选的值
rep[k-1]是指上一层选的，那如果上一层选的比这个小，那i就不选
因为咱们是顺序输出，不能选4=1+2+1

题目
Description
银河帝国正走向覆亡。为保留文明的种子，你需要驾驶飞船将一批“颛家”从帝国首都护送至银河边缘的基地。
现在已知航线是一条直线，帝国首都为起点（坐标0），基地为终点（坐标L），在这条航线上有N个空间站可以补充飞船的能源。
第i个空间站的坐标为ai，飞船停靠在第i个空间站必须花费bi个银河币，同时让你的飞船能量恢复为最大值M。
出发前飞船的能量是满额的M，每一点能量都可以让飞船航行一个坐标单位。

现在你已经通过募捐(榨篇）获得了S个银河币，请计算下飞船能否到达基地。

输入格式
第一行输入四个个数字N,L,M,S；(1<=N<=200) (1<=L<=20000) (1<=M<=20000) (0<=S<=20000)
接下来N行，每行输入两个数字，ai，bi (0<=ai<=L) (0<=bi<=20000)

输出格式
仅一行，如果能到达基地，输出Yes，否则输出No

输入样例
1 10000 5000 20000
5000 20000

输出样例
Yes

提示
样例说明，飞船可以花费5000能量到达一号空间站，花光20000银河币补满能量后，再行驶5000到达基地。
程序设计和数据结构设计都要考虑边缘数据。例如本题目，可能存在无需补给就直接行驶到基地的情况，也能存在bi>s的情况。

**解题思路：**直接深搜，每走一步就判断能否走下一步，还要比较余额等

#include
using namespace std;
struct node 
{
	int a,b;//坐标，花费 
}space[250];
int OK;
int N,L,M,S;
void  dfs(int money,int energy,int pos,int space_num)
{
	if(pos+energy>=L)
	{
		OK=1;
		return ;
	}
	for(int i=space_num+1;i<=N;i++)
	{
		if(money>=space[i].b&&energy>=space[i].a-pos)
		{
			dfs(money-space[i].b,M,space[i].a,i);
		}
	}
}
int main()
{
	cin>>N>>L>>M>>S;
	for(int i=1;i<=N;i++)
	cin>>space[i].a>>space[i].b;
	if(M>=L)
	OK=1;
	else
	dfs(S,M,0,0);
	if(OK)
	cout<<"Yes"<<endl;
	else
	cout<<"No"<<endl;
	return 0;
}
、、、、
DFS而不是BFS，也可以DP+贪心，但是我不会

小易得到了一个仅包含大小写英文字符的字符串，该字符串可能不是回文串。（“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串，“asds”就不是回文串。）

小易可以在字符串尾部加入任意数量的任意字符，使其字符串变成回文串。

现在请你编写一个程序，程序要能计算出小易可以得到的最短回文串。

输入描述：

一行包括一个字符串s,1<|s|<1e3。
1
输出描述:

一行包括一个字符串，代表答案。
1
示例1：
输入：

noon
1
输出：

noon
1
示例2：

输入：

noo
1
输出：

noon
1
示例3：

输入：

helloworld
1
输出：

helloworldlrowolleh
1
分析：
从题意可以知道字符串中的最后一个字符，一定是在一个回文中的，
因为是把原字符串变成一个回文，根据回文的特点，最后一个字符要么是在一个回文中，要么就是新生成回文的中心
比如：asddsava 变成回文是asddsavasddsa
hello变成回文是hellolleh
所以就用循环依次判断i~n(0<i<字符串长度，n为最后一个字符的位置) 这段字符是否是回文，找到回文后把非回文部分倒过来添加到字符串后面，就得到了最终回文

代码

#include
using namespace std;

bool judge(int start,int end,string s){//判断该部分字符串 是否是回文 
	while(start<end){
		if(s[start]!=s[end]) break;
		start++;
		end--;
	}
	if(start==end||s[start]==s[end]) return true;//sds就会出现start=end这种情况||ss字符串就会出现start!=end
	return false;
}

int main(){
	string str;
	cin >> str;
	int end =  str.size()-1;//最后一个字符的位置 
	int start = end;
	for(int i=0;i<str.size();i++){
		if(judge(i,end,str)){ //如果是回文 
			start = i;
			break;
		}
	} 
	for(int i=start-1;i>=0;i--){
		str+=str[i];
	}
	cout << str << endl;
	return 0;
}

/
/
回文串这题很牛！
判断结束条件是start==end
如果是第一种就从i=start开始复制，如果不是回文串
start也就是=0了。！！！

★★这题很强!

给出一个不大于 9 的正整数 nn，输出 n\times nn×n 的蛇形方阵。

从左上角填上 1 开始，顺时针方向依次填入数字，如同样例所示。注意每个数字有都会占用 3 个字符，前面使用空格补齐。

输入格式
无

输出格式
无

输入输出样例
输入 #1 复制
4
输出 #1 复制
  1  2  3  4
 12 13 14  5
 11 16 15  6
 10  9  8  7
上手鉴定大膜你。

简要思路：一直向一个方向填，如果到头了或者“撞到别的数”了就转向。

好像没什么好说的了吧······

代码很好写了：

#include
using namespace std;
int num[109][109],n;
int main(){
	num[1][1]=1;//初始为1
	cin>>n;
	for(int i=1,j=1,tot=1;tot<n*n;){//一直填到n*n个数填完
		while(++j<=n&&!num[i][j])num[i][j]=++tot;--j;//向右
		while(++i<=n&&!num[i][j])num[i][j]=++tot;--i;//向下
		while(--j> 0&&!num[i][j])num[i][j]=++tot;++j;//向左
		while(--i> 0&&!num[i][j])num[i][j]=++tot;++i;//向上
		//注意上面几行末尾的处理(--j这种)，不满足前面条件才会退出，这样进入下一个循环时实际上变量会有点问题。
		//举个例子：第一行写完，j=n+1，然后进入第二个while就根本不是在填表了（歪了）。
	}
	for(int i=1;i<=n;++i,cout<<endl)for(int j=1;j<=n;++j)
	cout<<setw(3)<<num[i][j];//输出
	return 0;
}
Over.

此题虽小，却值得好好做，尤其是新手（理科国集dalao来学OI捞几个一等的请无视）。

PS：若干时间后如果学到了一个叫莫队的算法，请回来看看，会发现代码出奇的相似，虽然并没有什么联系。

看到这题开始我楞了一下，之后推导出的答案。

主要结合代码讲一下吧。

Code：

#include 
#include 
#include 
using namespace std;
int num = 1, a[12][12];
int main() {
	int n;
	cin >> n;
	int t = ceil(1.0 * n / 2);根据推导总结，转的圈数为行数除以2，如果行数是奇数还要+1，其实就是ceil。
	for(int i=0; i<t; i++) {
		for (int j = i; j < n - i; j++) {
            a[i][j] = num++;//每一圈判断第一行
        }
        for (int j = i + 1; j < n - i - 1; j++) {
            a[j][n - i - 1] = num++;//每一圈判断最后一列
        }
        for (int j = n - i - 1; j > i; j--) {
            a[n - i - 1][j] = num++;//判断每一圈最后一行
        }
        for (int j = n - i - 1; j > i; j--)  {
            a[j][i] = num++;//判断每一圈第一列
        }
	}
	for(int i=0; i<n; i++) {
		for(int j=0; j<n; j++) {
			printf("%3d", a[i][j]);//输出方式要注意，%3d
		}
		printf("\n");
	}
	return 0;
} 

STL函数is_sort的原型：
第一个是，is_sorted(v1.begin(),v1.end())
s_sorted_until
第二个是，返回第一个破坏序列有序的元素迭代器。
auto it=is_sorted_until(v1.begin(),v1.end());
	if(it==v1.end())
		cout<<"v1 is sorted!"<<endl;
	
	auto it2=is_sorted_until(v2.begin(),v2.end());
	cout<<"v2 the return is "<<*it2<<endl;
 
https://blog.csdn.net/qq844352155/article/details/39337945

B. Permutation Sort
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given a permutation a consisting of n numbers 1, 2, ..., n (a permutation is an array in which each element from 1 to n occurs exactly once).

You can perform the following operation: choose some subarray (contiguous subsegment) of a and rearrange the elements in it in any way you want. But this operation cannot be applied to the whole array.

For example, if a=[2,1,4,5,3] and we want to apply the operation to the subarray a[2,4] (the subarray containing all elements from the 2-nd to the 4-th), then after the operation, the array can become a=[2,5,1,4,3] or, for example, a=[2,1,5,4,3].

Your task is to calculate the minimum number of operations described above to sort the permutation a in ascending order.

Input
The first line contains a single integer t (1≤t≤2000) — the number of test cases.

The first line of the test case contains a single integer n (3≤n≤50) — the number of elements in the permutation.

The second line of the test case contains n distinct integers from 1 to n — the given permutation a.

Output
For each test case, output a single integer — the minimum number of operations described above to sort the array a in ascending order.

Example
inputCopy
3
4
1 3 2 4
3
1 2 3
5
2 1 4 5 3
outputCopy
1
0
2
Note
In the explanations, a[i,j] defines the subarray of a that starts from the i-th element and ends with the j-th element.

In the first test case of the example, you can select the subarray a[2,3] and swap the elements in it.

In the second test case of the example, the permutation is already sorted, so you don't need to apply any operations.

In the third test case of the example, you can select the subarray a[3,5] and reorder the elements in it so a becomes [2,1,3,4,5], and then select the subarray a[1,2] and swap the elements in it, so a becomes [1,2,3,4,5].

题解：1525 B-置换排序
要解决这个问题，只需考虑几个例子：

如果数组已经排序，则答案是0;
如果a[1]=1(或a[n]=n)，则可以通过选择子数组在一次操作中对数组进行排序。[1,n−1](或[2,n]);
如果a[1]=n和a[n]=1，您可以执行操作顺序。[1,n−1], [2,n]和[1,n−1]并对每个数组进行排序(因为不能同时移动两个数组，所以不能更快地进行排序)。n就位n和1就位1只在2行动)；
否则，可以将数组排序到2行动。

#include 

using namespace std;

int main() {
  int t;
  scanf("%d", &t);
  while (t--) {
    int n;
    scanf("%d", &n);
    vector<int> a(n);
    for (int &x : a) scanf("%d", &x);
    int ans = 2;
    if (is_sorted(a.begin(), a.end()))
      ans = 0;
    else if (a[0] == 1 || a[n - 1] == n)
      ans = 1;
    else if (a[0] == n && a[n - 1] == 1)
      ans = 3;
    printf("%d\n", ans);
  }
}

int GCD(int a , int b){ 
if(a%b==0) return b; else return GCD(b,a%b); }
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
最大公约数


//
int lcm(int a, int b) { return a / gcd(a, b) * b; }

蓝桥杯E
解题思路

比赛时也没想太多，就跑最短路算法就就行了，迪杰斯特拉写着太麻烦，还不如安心跑弗洛伊德，差不多二十多秒出答案也挺爽的（主要是写的快）

或者考虑DP，只需要先建图，设 d [ i ] d[i] d[i]代表节点 i i i到节点 1 1 1的最短距离，那么显然状态转移方程为 d [ i ] = m i n ( d [ i ] , d [ j ] + g [ i ] [ j ] ) , j ∈ [ i − 21 , i − 1 ] d[i] = min(d[i], d[j] + g[i][j]), j \in [i - 21,i - 1] d[i]=min(d[i],d[j]+g[i][j]),j∈[i−21,i−1]，边界为 d [ 1 ] = 0 d[1] = 0 d[1]=0其余初始化为 i n f inf inf。

答案：10266837

//Floyd
#include 

using namespace std;
#define ENDL "\n"
typedef long long ll;
const int Mod = 1e9 + 7;
const int maxn = 2e5 + 10;

int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

int lcm(int a, int b) { return a / gcd(a, b) * b; }

int g[2050][2050];

int main() {
    // freopen("in.txt","r",stdin);
    // freopen("out.txt","w",stdout);
    // ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n = 2021;
    memset(g, 0x3f, sizeof g);
    for (int i = 1; i <= n; i++) {
        g[i][i] = 0;
        for (int j = i + 1; j <= i + 21; j++) g[i][j] = g[j][i] = lcm(i, j);
    }
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (g[i][k] + g[k][j] < g[i][j]) {
                    g[i][j] = g[i][k] + g[k][j];
                }
    cout << g[1][n] << endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//DP
#include 

using namespace std;
#define ENDL "\n"
typedef long long ll;
const int Mod = 1e9 + 7;
const int maxn = 1e5 + 10;

int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

int lcm(int a, int b) { return a / gcd(a, b) * b; }

int g[2050][2050], d[2050];

int main() {
    // freopen("in.txt","r",stdin);
    // freopen("out.txt","w",stdout);
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    memset(g, 0x3f, sizeof g);
    memset(d, 0x3f, sizeof d);
    for (int i = 1; i <= 2021; i++) {
        for (int j = i + 1; j <= i + 21; j++) g[i][j] = g[j][i] = lcm(i, j);
    }
    d[1] = 0;
    for (int i = 2; i <= 2021; i++) {
        for (int j = i - 1; j >= i - 21 && j > 0; j--) {
            d[i] = min(d[i], d[j] + g[i][j]);
        }
    }
    cout << d[2021] << endl;
    return 0;
}

我的思路：
哎，万万没想到，第二个编程题直接来个dp，蓝桥杯啊，你变了啊，做往年的省赛b组题基本没遇到过dp，去年考了dp也只是在填空里考了，今年直接第二道编程考dp，哎，菜是原罪！
看了半天没思路，又看了看测试样例范围 50%的样例在1<=n<=15,果断dfs深搜骗分，，，
input_case:
3
1 4 6
output_case:
10
code：

#include
using namespace std;

int n;
int w[102];
int flag[102];
set<int> ans;
int ff=0;
void dfs(int sum1,int sum2){
    if(sum1<sum2)return ;
    else{
        if(sum1>sum2){
            ans.insert(sum1-sum2);
        }
    }
    for(int i=1;i<=n;i++){
        if(!flag[i]){
            flag[i]=1;
            dfs(sum1+w[i],sum2);
            dfs(sum1,sum2+w[i]);
            flag[i]=0;
        }
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&w[i]);
    }
    dfs(0,0);
    printf("%d",ans.size());
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
贴一下正确解：

#include
using namespace std;
typedef long long ll;
int dp[102][100002];

int main()
{
    int n;
    scanf("%d",&n);
    int w[n+1];
    ll sum=0;
    for(int i=1;i<=n;i++){
        scanf("%d",&w[i]);
        sum+=w[i];
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=sum;j++){
            dp[i][j]=dp[i-1][j];
            if(dp[i][j]==0){
                if(w[i]>j)dp[i][j]=dp[i-1][w[i]-j];
                if(w[i]==j)dp[i][j]=1;
                if(w[i]<j)dp[i][j]=dp[i-1][j-w[i]];
            }
        }
    }

    ll ans=0;
    for(int i=1;i<=sum;i++){
        if(dp[n][i])ans++;
    }
    printf("%lld",ans);
    return 0;
}

小易得到了一个仅包含大小写英文字符的字符串，该字符串可能不是回文串。（“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串，“asds”就不是回文串。）

小易可以在字符串尾部加入任意数量的任意字符，使其字符串变成回文串。

现在请你编写一个程序，程序要能计算出小易可以得到的最短回文串。

输入描述：

一行包括一个字符串s,1<|s|<1e3。
1
输出描述:

一行包括一个字符串，代表答案。
1
示例1：
输入：

noon
1
输出：

noon
1
示例2：

输入：

noo
1
输出：

noon
1
示例3：

输入：

helloworld
1
输出：

helloworldlrowolleh
1
分析：
从题意可以知道字符串中的最后一个字符，一定是在一个回文中的，
因为是把原字符串变成一个回文，根据回文的特点，最后一个字符要么是在一个回文中，要么就是新生成回文的中心
比如：**asddsava 变成回文是asddsavasddsa**
hello变成回文是hellolleh
所以就用循环依次判断i~n(0<i<字符串长度，n为最后一个字符的位置) 这段字符是否是回文，找到回文后把非回文部分倒过来添加到字符串后面，就得到了最终回文

代码

#include
using namespace std;

bool judge(int start,int end,string s){//判断该部分字符串 是否是回文 
	while(start<end){
		if(s[start]!=s[end]) break;
		start++;
		end--;
	}
	if(start==end||s[start]==s[end]) return true;//sds就会出现start=end这种情况||ss字符串就会出现start!=end
	return false;
}

int main(){
	string str;
	cin >> str;
	int end =  str.size()-1;//最后一个字符的位置 
	int start = end;
	for(int i=0;i<str.size();i++){
		if(judge(i,end,str)){ //如果是回文 
			start = i;
			break;
		}
	} 
	for(int i=start-1;i>=0;i--){
		str+=str[i];
	}
	cout << str << endl;
	return 0;
}

注意其中的str+=str[i];

https://www.luogu.com.cn/problem/solution/P1087
FBI树
之前一直非常困惑，不知道怎么样才能从叶子推回节点
#include 
int n;  
long s=1;
char a[1027];
void print(int i)
{
    if(i >= 2*s-1)
        return ;
    print(i*2+1);
    print(i*2+2);
    printf("%c",a[i]);
}
int main()
{
    scanf("%d",&n);
    int i;
    getchar();
    for(i=1; i<= n; i++)
        s *= 2;
    for(i=s-1; i<s*2-1; i++)
    {
        char c;
        c = getchar();
        if(c == '0')
            a[i] = 'B';
        else
            a[i] = 'I';
    }
    for(i=s-2; i>=0; i--)
        if(a[i*2+1] == 'B' && a[i*2+2] == 'B')
            a[i] = 'B';
        else if(a[i*2+1] == 'I' && a[i*2+2] == 'I')
            a[i] = 'I';
        else
            a[i] = 'F';
    a[2*s-1] = '\0';
    print(0);
    printf("\n");
    return 0;
}

上面是用一位数组存了这颗FBI树的0，1.u空出来前面的用for循环一个个倒推
前面的非终端节点，，最后print函数左中递归后打印，就是典型的后序输出了。

#include 
using namespace std;
char s[1050];
void maketree(int x,int y){
    if(y>x){
        maketree(x,(x+y)/2);
        maketree((x+y+1)/2,y);
    }    
    int B=1,I=1;
    for(int i=0;i<=y-x;i++){
        if(s[x+i]=='1'){
            B=0;
        }else if(s[x+i]=='0'){
            I=0;
        }
    }
    if(B){
        cout<<'B';
    }else if(I){
        cout<<'I';
    }else{
        cout<<'F';
    }
}
int main() {
    int n;
    cin>>n>>s;
    maketree(0,(1<<n)-1);
    return 0;
}
这个代码是二分递归。左右分别遍历到最后

vectora(n+1,0); 用0初始化有n+1个单位的数组a；

*/8644 堆排序
时间限制:1000MS  代码长度限制:10KB
提交次数:1909 通过次数:1257

题型: 编程题   语言: G++;GCC
Description
用函数实现堆排序，并输出每趟排序的结果



输入格式
第一行：键盘输入待排序关键的个数n
第二行：输入n个待排序关键字，用空格分隔数据


输出格式
第一行：初始建堆后的结果
其后各行输出交换堆顶元素并调整堆的结果，数据之间用一个空格分隔


输入样例
10
5 4 8 0 9 3 2 6 7 1


输出样例
9 7 8 6 4 3 2 5 0 1
8 7 3 6 4 1 2 5 0 9
7 6 3 5 4 1 2 0 8 9
6 5 3 0 4 1 2 7 8 9
5 4 3 0 2 1 6 7 8 9
4 2 3 0 1 5 6 7 8 9
3 2 1 0 4 5 6 7 8 9
2 0 1 3 4 5 6 7 8 9
1 0 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
*/
#include
#include
#include
using namespace std;


//n是总结点数，x是当前需要堆化的结点
void singleheapify(int a[],int last,int x)//对一个结点进行堆化
{

   int max = x;//max存放（x和他的儿子共3个结点）全家人中的最大值
   int lch=2*x+1;//左儿子刚好就是这个
   int rch=2*x+2;//右儿子刚好就是这个

   if(a[max]<a[lch]&&lch<=last) max = lch;

   if(a[max]<a[rch]&&rch<=last) max = rch;//这一步千万千万不要加else
   /*结合上一步的if，这两个if其实是在找x和儿子三个人之间的最大值，找到了再去交换，
   否则我们交换了一边，另一边可能是不满足父亲值最大的*/

   if(max != x)//儿子比父亲大，要交换
   {
       swap(a[max],a[x]);
       
       singleheapify(a,last,max);/*以当前max指向的下标为父亲，
       继续看看符不符合大根堆的要求*/
   }

}

void allheapify(int a[],int last)//全部节点堆化
{

    int lastparent = (last-1) / 2;//找到最后一个非叶子节点的下标

    //从最后一个非叶子节点开始枚举，在这之前的结点全是有儿子的结点
    for(int j=lastparent;j>=0;j--)singleheapify(a,last,j);
}

void heapsort(int a[],int last)//堆排序重点部分！！！！！
{
    allheapify(a,last);//把原数组堆化，使其各节点都满足堆的要求

    for(int i=last;i>=1;i--)//枚举大根堆的最后一个结点，一直枚举直到1就结束，//
    {                       /*大根堆在不断减小，
                          相当于分别在0~last，0~last-1,0~last-2，......0~1中找最大值，
                         每一次将所找到的最大值放到数组后面*/
        for(int j=0;j<=last;j++) printf("%d ",a[j]);cout<<endl;

        swap(a[0],a[i]);/*生成了一个大根堆因此具有根节点值最大的性质，
        利用这个性质我们把根节点放数组最后*/

        singleheapify(a,i-1,0);/*，当前根节点已经发生变化，
        即不是最大值而是最后一个结点交换上来的，
        结合上一步，这两步相当于把0~i范围内的最大值移出去，
        减小大根堆规模，当前只考虑0~i-1范围内最大值，在新的范围里面再次构建大根堆*/
    }
}

int main()
{
   int n,a[500];
   scanf("%d",&n);
   for(int i=0;i<=n-1;i++) cin>>a[i];
   heapsort(a,n-1);
   for(int j=0;j<=n-1;j++) cout<<a[j]<<" ";

  return 0;
}

*/8645 归并排序（非递归算法）Description
用函数实现归并排序（非递归算法），并输出每趟排序的结果



输入格式
第一行：键盘输入待排序关键的个数n
第二行：输入n个待排序关键字，用空格分隔数据


输出格式
每行输出每趟排序的结果，数据之间用一个空格分隔


输入样例
10
5 4 8 0 9 3 2 6 7 1


输出样例
4 5 0 8 3 9 2 6 1 7
0 4 5 8 2 3 6 9 1 7
0 2 3 4 5 6 8 9 1 7
0 1 2 3 4 5 6 7 8 9
*/
#include 
using namespace std;
void merge(int *a,int start,int mid,int last)//每一个跨度span的左右数组合并
{
    int l=start;//看成原本归并排序中的左数组的最左边的下标
    int r=mid+1;//看成原本归并排序中的右数组的最左边的下标
    int b[last-start+1],j=0;

    while(l<=mid&&r<=last)
    {
        if(a[l]<=a[r]) b[j++]=a[l++];
        else b[j++]=a[r++];
    }
    while(l<=mid) b[j++]=a[l++];
    while(r<=last) b[j++]=a[r++];
    for(int i=0;i<j;i++) a[start++]=b[i];
}
void split(int *a,int span,int length)//按照span对整个数组逐步进行自下而上的合并
{
    int curindex=0;
    while(curindex+2*span-1<length)//右数组不能超过a数组长度
    {
        merge(a,curindex,curindex+span-1,curindex+2*span-1);
        curindex+=2*span;
    }
    if(curindex+span-1<length-1) merge(a,curindex,curindex+span-1,length-1);
    //这里没把-1约掉是为了方便看出二者关系，即右数组不够一个跨度，我们要特殊地合并
}
void mergesort(int *a,int length)//确定每一次合并的跨度span
{
    int span=1;
    while(span<length)//大于length的合并无意义
    {
        split(a,span,length);//按照这个跨度对整个数组逐步进行合并
        for(int i=0;i<length;i++) cout<<a[i]<<" ";//每完成一次合并打印一次
        cout<<endl;
        span*=2;
    }
}
int main()
{
    int n,a[100];
    cin>>n;
    for(int i=0;i<=n-1;i++) cin>>a[i];
    mergesort(a,n);
}

19011 小猿的依赖循环
时间限制:1000MS  代码长度限制:10KB
提交次数:0 通过次数:0

题型: 编程题   语言: G++;GCC
Description
猿辅导2021校园招聘笔试（算法二） 
小猿在加载一个网页，这个网页共需要N个相关资源，这些资源之间有一些依赖关系。
如果这些资源中存在循环依赖，我们认为这个网页不能加载成功，否则可以加载成功。
存在循环依赖是指，这些资源中存在资源X，X依赖的资源Y直接或间接依赖于X。
你能帮助小猿判断一下这个网页能否加载成功吗？



输入格式
第一行输入T（T ≤ 10），表示输入T组数据。
每组数据第1行，输入一个数N（1 ≤ N ≤ 500）表示该组case有编号为1~N的N项资源。
每组数据第2到 N+1 行，输入一个 N*N 的零一矩阵。
矩阵第 i 行第 j 列数字为 a[i][j] 表示编号为 i 的资源是否依赖于编号为 j 的资源，1表示依赖，0表示不依赖。数据保证a[i][i] = 0。


输出格式
输出包含T行，每行输出对应每组case中是否存在循环依赖。存在输出1，不存在输出0。


输入样例
2
3
0 1 0
0 0 1
1 0 0
3
0 1 0
0 0 0
0 0 0


输出样例
1
0

思路2：使用dfs优先遍历搜索来查看是否产生了循环。
注意事项：不能够直接dfs（0）,即所有的未走过的节点都要进行一次dfs，即图中的连通图的dfs遍历方式。即会有一种情况产生：a、b、c之间没有产生循环依赖，且a、b、c都没有依赖d和e，但是d和e却产生了依赖。但是如果只有一个dfs（0）就会产生错误，误以为这组数据没有产生循环依赖，事实却是产生了循环依赖，只是恰巧不在dfs（0）可以遍历到的范围之内罢了。
AC代码：

#include
using namespace std;
int n, t;
int p[505][505];
bool pd[505];
int ans = 0;
void init(int x) {
	for (int i = 0; i < x; i++) {
		for (int j = 0; j < x; j++) {
			p[i][j] = 0;
		}
		pd[i] = false;
	}
	ans = 0;
}

void dfs(int x) {
	if (pd[x] == true) {
		ans = 1;
		return;
	}
	pd[x] = true;
	for (int i = 0; i < t; i++) {
		if (p[x][i] == 1) {
			dfs(i);
		}
	}
	pd[x] = false;
}
int main() {
	cin >> n;
	while (n != 0) {
		cin >> t;
		init(t);
		for (int i = 0; i < t; i++) {
			for (int j = 0; j < t; j++) {
				cin >> p[i][j];
			}
		}
		//dfs(0);
		//上面这行代码就是只从0这个点开始导致了错误。
		//下面这部分for循环代码就是为了能够遍历所有的未走过的节点，由此得出的答案才是正确答案。
		for (int i = 0; i < t; i++) {
			if (pd[i] == false) {
				dfs(i);
				if (ans == 1) {
					break;
				}
			}
		}
		cout << ans << endl;
		n--;
	}
	return 0;
}

CF爆零心态爆炸21-5-28

https://codeforces.com/contest/1526/problem/A
outputstandard output
You are given an array a of 2n distinct integers. You want to arrange the elements of the array in a circle such that no element is equal to the the arithmetic mean of its 2 neighbours.

More formally, find an array b, such that:

b is a permutation of a.

For every i from 1 to 2n, bi≠bi−1+bi+12, where b0=b2n and b2n+1=b1.

It can be proved that under the constraints of this problem, such array b always exists.
///
注意，数组大小是偶数长度。通常在这类问题中，我们会把数组分成两个相等的部分。你能算出这两部分是什么吗?





我们对数组进行排序，把它分成大的一半和小的一半。



主要思想是我们可以把数字分成两半，大的一半和小的一半，我们可以把大的一半放在奇数位置小的一半放在偶数位置。



这是可行的，因为最小的大数比最大的小数大。因此，任意两个小数的均值都小于任意一个大数，任意两个大数的均值都大于任意一个小数。
#include
#include
using namespace std;
int a[100];
int main(){
    //std::ios::sync_with_stdio(false);
    //cin.tie(0);
    int t;cin>>t;
    while(t--){
        int n;cin>>n;
        for(int i=1;i<=2*n;i++){
            cin>>a[i];
        }
        sort(a+1,a+1+2*n);
        for(int i=1;i<=n;i++){
            cout<<a[i]<<' '<<a[i+n]<<' ';
        }
        cout<<endl;
    }
    return 0;
}

outputstandard output
You are given an integer x. Can you make x by summing up some number of 11,111,1111,11111,…? (You can use any number among them any number of times).

For instance,

33=11+11+11
144=111+11+11+11
//
https://codeforces.com/contest/1526/problem/B
Read the name of the problem ;)

Hint 1
1111=11⋅101
Hint 2
All numbers other than 11 and 111 are useless.

题解：
方法1

请注意，1111=11⋅100+11，同理，11111=111⋅100+11。这意味着我们可以只用11和111来构造1111和所有更大的数。所以它足以检验我们是否可以只从11和111构造X。



假设X=A⋅11+B⋅111，其中A,B≥0。假设B=C⋅11+D，其中D<11。那么X = (A + C⋅111)⋅11 + D⋅111。所以我们可以强制所有11个D值来检查X是否可以得到。



方法2

由于gcd(11111)=1，根据麦乐鸡定理，所有大于1099的数都可以写成11和111的和。我们可以使用蛮力找出所有小于或等于1099的值的答案，并对所有其他数字回答yes。
#include
#include
using namespace std;
#define ting getchar();getchar()
int a[100];
int main(){
    //std::ios::sync_with_stdio(false);
    //cin.tie(0);
    int t;cin>>t;
    while(t--){
        long long n;cin>>n;
        long long k=n/11;
        long long a2=n-k*11;
        if(a2*10<=k){
            cout<<"YES"<<endl;
        }
        else{
            cout<<"NO"<<endl;
        }
    }
    return 0;
}

outputstandard output
This is the hard version of the problem. The only difference is that in this version n≤200000. You can make hacks only if both versions of the problem are solved.

There are n potions in a line, with potion 1 on the far left and potion n on the far right. Each potion will increase your health by ai when drunk. ai can be negative, meaning that potion will decrease will health.

You start with 0 health and you will walk from left to right, from first potion to the last one. At each potion, you may choose to drink it or ignore it. You must ensure that your health is always non-negative.

What is the largest number of potions you can drink?
#include
#include
#include
using namespace std;
#define ting getchar();getchar()
long long dp[200005];//dp[i]表示i长度的最小负数和
long long a[200005];
long long sum[200005];
priority_queue<long long,vector<long long>,greater<long long> >que;
int main(){
    //std::ios::sync_with_stdio(false);
    //cin.tie(0);
 
    int n;cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    long long sum=0;
    long long zhenlen=0;
    long long fulen=0;
    long long sumf=0;
    long long maxn=-1;
    for(int i=1;i<=n;i++){
        if(a[i]>=0){
            sum+=a[i];
            zhenlen++;
        }
        else{
            if(sum+sumf+a[i]>=0){
                que.push(a[i]);
                fulen++;
                sumf+=a[i];
            }
            else{
                if(!que.empty()&&a[i]>que.top()){
                    sumf-=que.top();
                    que.pop();
                    que.push(a[i]);
                    sumf+=a[i];
                }
            }
        }
        maxn=max(maxn,fulen+zhenlen);
    }
    cout<<maxn;
    return 0;
}

#include
#include
using namespace std;
#define ting getchar();getchar()
long long dp[2005];
long long a[2005];
int main(){
    //std::ios::sync_with_stdio(false);
    //cin.tie(0);
 
    int n;cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    int len=0;
    for(int i=1;i<=n;i++){
        if(dp[len]+a[i]>=0){
            dp[len+1]=dp[len]+a[i];
            len++;
        }
        for(int j=len;j>=1;j--){
            if(dp[j-1]+a[i]>dp[j]){
                dp[j]=dp[j-1]+a[i];
            }
        }
    }
    cout<<len;
    return 0;
}

https://codeforces.com/contest/1526/problem/C1
outputstandard output
This is the easy version of the problem. The only difference is that in this version n≤2000. You can make hacks only if both versions of the problem are solved.

There are n potions in a line, with potion 1 on the far left and potion n on the far right. Each potion will increase your health by ai when drunk. ai can be negative, meaning that potion will decrease will health.

You start with 0 health and you will walk from left to right, from first potion to the last one. At each potion, you may choose to drink it or ignore it. You must ensure that your health is always non-negative.

What is the largest number of potions you can drink?

std::ios::sync_with_stdio(false);
　　很多C++的初学者可能会被这个问题困扰，经常出现程序无故超时，最终发现问题处在cin和cout上，（甚至有些老oier也会被这个问题困扰，每次只能打scanf和printf，然后一堆的占位符巨麻烦），这是因为C++中，cin和cout要与stdio同步，中间会有一个缓冲，所以导致cin，cout语句输入输出缓慢，这时就可以用这个语句，取消cin，cout与stdio的同步，说白了就是提速，效率基本与scanf和printf一致。然后就可放心的使用cin，cout了。（不过实际上使用了using namespace std;之后就可以直接打ios::sync_with_stdio(false);了）

今天遇到有人问问题说关闭流同步以后会炸空间，我也很诧异。然后看了下代码，问题出在scanf()。取消流同步以后，stdio中带有的scanf()和printf()输入输出的内部同步也会被取消（大概是这样的，如果有误请联系博主更正），这时候再用scanf()和printf()就可能会出玄学错误，所以用的时候也要注意。

　　另外，如果使用文件输入输出的话，一定记住要把这条语句放在freopen()后面，反正也会出西西，但是具体问题博主也不太清楚。。。

18935 贪吃的小Q
时间限制:1000MS  代码长度限制:10KB
提交次数:0 通过次数:0

题型: 编程题   语言: G++;GCC
Description
腾讯2018春招技术类编程题

小Q的父母要出差N天，走之前给小Q留下了M块巧克力。
小Q决定每天吃的巧克力数量不少于前一天吃的一半，但是他又不想在父母回来之前的某一天没有巧克力吃，
请问他第一天最多能吃多少块巧克力？



输入格式
一行包含两个正整数，表示父母出差的天数N(N<=50000)和巧克力的数量M(N<=M<=100000)


输出格式
输出一个数表示小Q第一天最多能吃多少块巧克力。


输入样例
3 7


输出样例
4


作者 30002692 

#include
#include
#include
#include
#include
#include
#include
using namespace std;
int n,m;
int sum(int s)
{
    int sum1=0;
    int i=0;
    for(i=0;i<n;i++)
    {
        sum1+=s;
        s=(s+1)/2;
    }
    return sum1;
}

int erfen()
{
    if(n==1) return m;
    int l=1,r=m,middle;
    while(l<=r)
    {
        middle=(l+r)/2;
        if(sum(middle)==m) return middle;
        else if(sum(middle)<m) l=middle+1;
        else r=middle-1;
    }
    return  r;
}

int main()
{
       cin>>n>>m;
       int ans=erfen();
       cout<<ans;
       return 0;
}
18935 贪吃的小Q
时间限制:1000MS  代码长度限制:10KB
提交次数:0 通过次数:0

题型: 编程题   语言: G++;GCC
Description
腾讯2018春招技术类编程题

小Q的父母要出差N天，走之前给小Q留下了M块巧克力。
小Q决定每天吃的巧克力数量不少于前一天吃的一半，但是他又不想在父母回来之前的某一天没有巧克力吃，
请问他第一天最多能吃多少块巧克力？



输入格式
一行包含两个正整数，表示父母出差的天数N(N<=50000)和巧克力的数量M(N<=M<=100000)


输出格式
输出一个数表示小Q第一天最多能吃多少块巧克力。


输入样例
3 7


输出样例
4
思路：你如果最后面一天一块那样去推的话，你也得用二分呀，二分他吃一块的天数
其实他就是第一天是一个最大的数，然后第二天就乘1/2，第三天再乘1/2，直到后面一长串1
比如有7块，那答案就是在1-7
然后中间值是4
然后就判断4能不能成立，4太多范围就缩小到1-3，太少就缩小到5-7

伐木工人米尔科需要砍倒M米长的木材。这是一个对米尔科来说很容易的工作，因为他有一个漂亮的新伐木机，可以像野火一样砍倒森林。不过，米尔科只被允许砍倒单行树木。

米尔科的伐木机工作过程如下：米尔科设置一个高度参数H（米），伐木机升起一个巨大的锯片到高度H，并锯掉所有的树比H高的部分（当然，树木不高于H米的部分保持不变）。米尔科就行到树木被锯下的部分。

例如，如果一行树的高度分别为20，15，10和17，米尔科把锯片升到15米的高度，切割后树木剩下的高度将是15，15，10和15，而米尔科将从第1棵树得到5米，从第4棵树得到2米，共得到7米木材。

米尔科非常关注生态保护，所以他不会砍掉过多的木材。这正是他为什么尽可能高地设定伐木机锯片的原因。帮助米尔科找到伐木机锯片的最大的整数高度H，使得他能得到木材至少为M米。换句话说，如果再升高1米，则他将得不到M米木材。

输入格式
第1行：2个整数N和M，N表示树木的数量（1<=N<=1000000）,M表示需要的木材总长度（1<=M<=2000000000）

第2行：N个整数表示每棵树的高度，值均不超过1000000000。所有木材长度之和大于M，因此必有解。

输出格式
第1行：1个整数，表示砍树的最高高度。

输入输出样例
输入 #1 复制
5 20
4 42 40 26 46
输出 #1 复制
36

可以二分一下
#include
using namespace std;
long long n,bz,s=0,mid,leftt,longest,trees[1000008];
int main()
{
    scanf("%lld%lld",&n,&bz); 
    for(int i=1;i<=n;i++) 
    {
        scanf("%lld",&trees[i]);
        longest=max(longest,trees[i]);//找到最长木材 
    }
    while(leftt<=longest)
    {
        mid=(leftt+longest)/2; //从中间点开始作为伐木机高度
        s=0; 
        for(int i=1;i<=n;i++) 
			if(trees[i]>mid) //树的高度大于伐木机高度 
				s+=trees[i]-mid; //高的部分累加 
        if(s<bz) //木材不足 
			longest=mid-1;//在左边搜 减小高度增加木材 
		else 
			leftt=mid+1;//在右边搜 增加高度减小木材 
    }
    cout<<leftt-1; 
    return 0;
}

特别方法，sort后实时看符不符合，不符合从大向小找，没找一次加一次，
#include
#include
#include
using namespace std;
int tree[1000001];
int n,m;
int main()
{
    int i,num,ans;
    long long sum;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)
        scanf("%d",&tree[i]);
    sort(tree+1,tree+n+1);
    sum=0;
    num=n;
    while(sum<m)
    {
        sum+=(tree[num]-tree[num-1])*(n-num+1);
        num--;
    }
    num++;
    ans=tree[num-1]+(sum-m)/(n-num+1);
    printf("%d\n",ans);
    return 0;
}