LM优化算法

LM优化算法，是一种非线性优化算法，其可以看作是梯度下降和高斯牛顿法的结合。综合了梯度下降对初值不敏感和高斯牛顿在最优值附近收敛速度快的特点。

本人非数学专业，且对算法理解可能不到位，详细的算法推导及各个优化算法之间的关系，非常推荐看METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS ，其介绍更详细也更专业。

以下简要介绍LM算法，然后给出opencv中有关的实现。

本文代码也是来自opencv相关代码，位置在opencv-master\modules\calib3d\src\calibration.cpp\cvFindExtrinsicCameraParams2()。

当然，有关LM算法的实现，在opencv的usac模块中有更为正式的实现，在该模块中，对许多算法进行了集成和优化，后续再进行研究。

理论知识

对于一个最小二乘问题，有：

$$\begin{gathered} F(x)=\frac{1}{2}\sum _{i=1}^m(f_i(x){)}^2 \\ {f}_i(x)为残差 \end{gathered}$$
我们的目的是求解残差f(x)的一组系数，使目标函数（或代价函数）F(x)达到最小值。通常的做法是，给定一个初值x0，优化算法不断的迭代，产生x1,x2,…，最终收敛于X。

因此，在这个收敛的过程中，我们需要两样东西，即方向h和步长α
$$\begin{gathered} x_{k+1}=x_k+\alpha h_d \\ {h}_d即为收敛的方向 \\ \alpha 即为收敛的步长 \end{gathered}$$
所以，我们看到的梯度下降、高斯牛顿以及本文说的LM算法，其思想都是一致的。

梯度下降

这里给出梯度下降的公式，有：
$$\begin{gathered} x_{k+1}=x_k-\alpha \dot{F}(x) \\ \dot{F}(x)为F(x)一阶导数 \end{gathered}$$

高斯牛顿

高斯牛顿是在牛顿迭代的基础上，用雅可比矩阵的平方来近似Hessian矩阵，求解起来将会更加高效（大多数情况下，Hessian矩阵太难求）。这样做的缺点就是，要求迭代初值必须在最优解附近，否则以上假设将不成立。这里给出其公式：
$$\begin{gathered} x_{k+1}=x_k+\alpha h_{gn} \\ {J}^{T}J{h}_{gn}=-J^{T}f \end{gathered}$$

Levenberg–Marquardt

给出其公式：
$$\begin{gathered} x_{k+1}=x_k+\alpha h_{lm} \\ (J^{T}J+\mu I)h_{lm}=-J^{T}f \end{gathered}$$
在有些情况下，JtJ不可逆，导致高斯牛顿无法使用。LM通过将JtJ加上一个μI（I为单位阵），保证了正规方程的左侧一定可逆。

在算法实际的应用中，通过调节μ的大小，可以使算法在梯度下降和高斯牛顿两者之间切换，如：

• 使用较大的μ值，算法可以看作梯度下降，适合当前优化位置距离最优解较远的情况
• 使用较小的μ值，算法可以看作高斯牛顿，适合当前优化位置接近最优解。

算法框架

LM算法通过求解正规方程，得到每次迭代的步长和方向。因此，算法的主要目的是求解正规方程左右侧的项，然后通过SVD分解即可得到参数更新的步长及方向，即：

• JtJ - 雅可比矩阵的转置与其自己相乘
• JErr - 雅可比矩阵的转置与残差矩阵（向量）相乘

算法框架在外部计算雅可比矩阵和残差矩阵，然后在算法内部通过求解正规方程，得到每次参数更新的步长及方向。

然后利用更新的参数，在外部计算残差，然后判断残差是否朝着收敛方向进行。

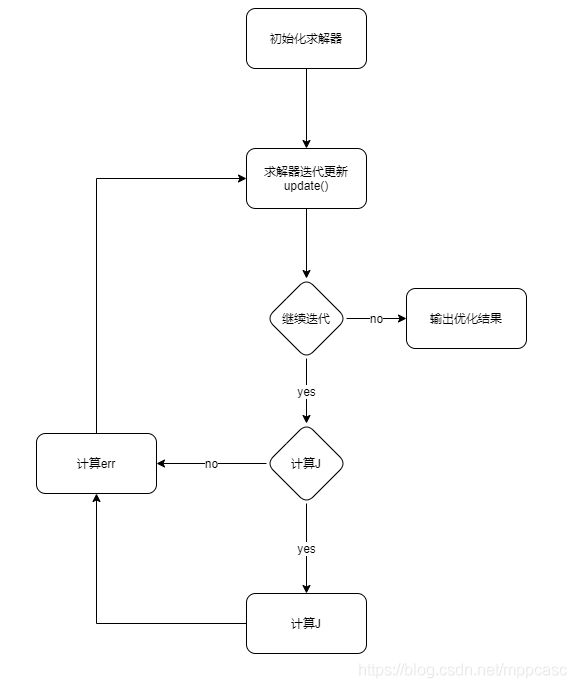
算法的整体流程

求解器update流程

求解器updata()内部根据不同的状态进行相应的计算，具体流程如下：

说明

• J表示雅可比矩阵
• err表示残差矩阵
• 求解器内外同步表示求解器内部和外部相应的参数指向相同，便于在求解器外部进行雅可比矩阵和残差矩阵的计算

算法实现

算法的实现主要步骤都体现在上述流程图中。

头文件

#pragma once

#include 

#include "opencv2/core/types_c.h"
#include "opencv2/core/core_c.h"

using namespace cv;

struct Iteration
{
	int iters = 0;
	TermCriteria criteria = TermCriteria(0, 0, 0);
	int lamda_lg10 = 0;

};

class LevMarq
{
public:
	LevMarq();
	LevMarq(int nparams, int nerrs,
		TermCriteria criteria = TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 30, DBL_EPSILON), bool completeSymmFlag = false);
	~LevMarq();

	void clear();

	void initParam(Mat params);

	void init(int nparams, int nerrs,
		TermCriteria criteria = TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 30, DBL_EPSILON), bool completeSymmFlag = false);

	bool update(const CvMat*& params, CvMat*& J, CvMat*& err);

	void step();

private:
	double m_lambda_lg10;

	enum {
		DONE,
		START,
		CALC_J,
		CHECK_ERR
	};

	int m_state;
	TermCriteria m_criteria;
	int m_iters;
	bool m_complete_symm_flag;
	double m_err_norm, m_prev_err_norm;
	int m_solver_method;

	const double m_log10 = log(10.);

	Ptr m_mask;
	Ptr m_params;
	Ptr m_prev_params;

	Ptr m_JtJ;
	Ptr m_JtErr;
	Ptr m_J;
	Ptr m_Err;

	Ptr m_avl_JtJ;
	Ptr m_avl_JtErr;
	Ptr m_avl_params;
};

cpp

#include "LevMarq.h"

static void subMatrix(const cv::Mat& src, cv::Mat& dst, const std::vector& cols,
	const std::vector& rows) {
	int nonzeros_cols = cv::countNonZero(cols);
	cv::Mat tmp(src.rows, nonzeros_cols, CV_64FC1);

	for (int i = 0, j = 0; i < (int)cols.size(); i++)
	{
		if (cols[i])
		{
			src.col(i).copyTo(tmp.col(j++));
		}
	}

	int nonzeros_rows = cv::countNonZero(rows);
	dst.create(nonzeros_rows, nonzeros_cols, CV_64FC1);
	for (int i = 0, j = 0; i < (int)rows.size(); i++)
	{
		if (rows[i])
		{
			tmp.row(i).copyTo(dst.row(j++));
		}
	}
}

LevMarq::LevMarq()
{
	// only do some init
	m_lambda_lg10 = 0;
	m_state = DONE;
	m_criteria = TermCriteria(0, 0, 0);
	m_iters = 0;
	m_complete_symm_flag = false;
	m_err_norm = m_prev_err_norm = DBL_MAX;
	m_solver_method = DECOMP_SVD;
}

LevMarq::LevMarq(int nparams, int nerrs, TermCriteria criteria, bool completeSymmFlag)
{
	init(nparams, nerrs, criteria, completeSymmFlag);
}

LevMarq::~LevMarq()
{
	clear();
}

void LevMarq::clear()
{
	m_mask.release();
	m_params.release();
	m_prev_params.release();

	m_JtJ.release();
	m_JtErr.release();
	m_J.release();
	m_Err.release();

	m_avl_JtJ.release();
	m_avl_JtErr.release();
	m_avl_params.release();
}

void LevMarq::initParam(Mat params)
{
	if (params.empty())
		return;

	double* data = m_params->data.db;
	assert(params.cols == 1, "params dim must be N*1");
	for (int i = 0; i < params.rows; i++)
	{
		data[i] = params.at(i, 0);
	}
}

/// 

/// create some mat used for store related
/// 
/// the nums of parameters to be optimized
/// the nums of residual function
/// condition of convergence 
/// 
void LevMarq::init(int nparams, int nerrs, TermCriteria criteria, bool completeSymmFlag)
{
	if (!m_params || m_params->rows != nparams || nerrs != (m_Err ? m_Err->rows : 0))
		clear();

	m_mask.reset(cvCreateMat(nparams, 1, CV_8U));
	cvSet(m_mask, cvScalarAll(1));
	m_prev_params.reset(cvCreateMat(nparams, 1, CV_64F));
	m_params.reset(cvCreateMat(nparams, 1, CV_64F));
	m_JtJ.reset(cvCreateMat(nparams, nparams, CV_64F));
	m_JtErr.reset(cvCreateMat(nparams, 1, CV_64F));

	if (nerrs > 0)
	{
		m_J.reset(cvCreateMat(nerrs, nparams, CV_64F));
		m_Err.reset(cvCreateMat(nerrs, 1, CV_64F));
	}

	m_err_norm = m_prev_err_norm = DBL_MAX;
	m_lambda_lg10 = -3;
	m_criteria = criteria;
	if (m_criteria.type & TermCriteria::COUNT)
	{
		m_criteria.maxCount = MIN(MAX(m_criteria.maxCount, 1), 100000);
	}
	else
	{
		m_criteria.maxCount = 30;
	}
	if (m_criteria.type & TermCriteria::EPS)
	{
		m_criteria.epsilon = MAX(m_criteria.epsilon, 0);
	}
	else
	{
		m_criteria.epsilon = DBL_EPSILON;
	}
	m_state = START;
	m_iters = 0;
	m_complete_symm_flag = completeSymmFlag;
	m_solver_method = DECOMP_SVD;
}

bool LevMarq::update(const CvMat*& params, CvMat*& J, CvMat*& err)
{
	J = err = 0;
	assert(!m_Err.empty());
	if (m_state == DONE)
	{
		params = m_params;
		return false;
	}
	if (m_state == START)
	{
		params = m_params;
		cvZero(m_J);
		cvZero(m_Err);
		J = m_J;
		err = m_Err;
		m_state = CALC_J;
		return true;
	}
	if (m_state == CALC_J)
	{
		cvMulTransposed(m_J, m_JtJ, 1);
		cvGEMM(m_J, m_Err, 1, 0, 0, m_JtErr, CV_GEMM_A_T);
		cvCopy(m_params, m_prev_params);
		step();

		if (m_iters == 0)
		{
			m_prev_err_norm = cvNorm(m_Err, 0, CV_L2);
		}
		params = m_params;
		cvZero(m_Err);
		err = m_Err;
		m_state = CHECK_ERR;
		return true;
	}

	assert(m_state == CHECK_ERR);
	m_err_norm = cvNorm(m_Err, 0, CV_L2);
	if (m_err_norm > m_prev_err_norm)
	{
		if (++m_lambda_lg10 <= 16)
		{
			step();

			params = m_params;
			cvZero(m_Err);
			err = m_Err;
			m_state = CHECK_ERR;
			return true;
		}
	}

	m_lambda_lg10 = MAX(m_lambda_lg10 - 1, -16);
	if (++m_iters >= m_criteria.maxCount ||
		cvNorm(m_params, m_prev_params, CV_RELATIVE_L2) <= m_criteria.epsilon)
	{
		std::cout << "criteria.epsilon: " << cvNorm(m_params, m_prev_params, CV_RELATIVE_L2) << std::endl;
		params = m_params;
		m_state = DONE;
		return true;
	}
	params = m_params;
	m_prev_err_norm = m_err_norm;
	cvZero(m_J);
	cvZero(m_Err);
	J = m_J;
	err = m_Err;
	m_state = CALC_J;
	return true;
}

void LevMarq::step()
{
	double miu = exp(m_lambda_lg10 * m_log10);
	int _nparams = m_params->rows;

	Mat _JtJ = cvarrToMat(m_JtJ);
	Mat _mask = cvarrToMat(m_mask);

	int _avl_nparams = countNonZero(_mask);
	if (!m_avl_JtJ || m_avl_JtJ->rows != _avl_nparams)
	{
		m_avl_JtJ.reset(cvCreateMat(_avl_nparams, _avl_nparams, CV_64F));
		m_avl_JtErr.reset(cvCreateMat(_avl_nparams, 1, CV_64F));
		m_avl_params.reset(cvCreateMat(_avl_nparams, 1, CV_64F));
	}

	Mat _avl_JtJ = cvarrToMat(m_avl_JtJ);
	Mat _avl_JtErr = cvarrToMat(m_avl_JtErr);
	Mat_ _avl_params = cvarrToMat(m_avl_params);

	subMatrix(cvarrToMat(m_JtErr), _avl_JtErr, std::vector(1, 1), _mask);
	subMatrix(_JtJ, _avl_JtJ, _mask, _mask);

	if (!m_Err)
		completeSymm(_avl_JtErr, m_complete_symm_flag);

	_avl_JtJ.diag() *= 1.0 + miu;
	std::cout << miu << std::endl;
	solve(_avl_JtJ, _avl_JtErr, _avl_params, m_solver_method);

	int j = 0;
	for (int i = 0; i < _nparams; i++)
	{
		m_params->data.db[i] = m_prev_params->data.db[i] - (m_mask->data.ptr[i] ? _avl_params(j++) : 0);
	}
}

算法调用

double param[opt_num] = { 0,0 }; // k1 p1
CvMat _param = cvMat(opt_num, 1, CV_64F, param);
CvTermCriteria criteria = cvTermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 10000, DBL_EPSILON);
myCvLevMarq solver(opt_num, total, criteria);
solver.initParam(distCoffes.rowRange(Range(0,2)));

int cnt = 0;
for (;;)
{
    const CvMat* __param = 0;
    CvMat* J = 0, * err = 0;
    bool proceed = solver.update(__param, J, err);
    cvCopy(__param, &_param); // 将优化的变量保存下来
    if (!proceed || !err)
        break;

    if (J)
    {
        // 计算雅可比矩阵和残差矩阵
    }
    else
    {
        //残差矩阵
    }
}