入门机器学习（西瓜书+南瓜书）线性回归和逻辑回归总结（python代码实现）

入门机器学习（西瓜书+南瓜书）线性回归和逻辑回归总结（python代码实现）

一、线性回归理论总结

1.1 通俗理解

通俗理解的线性回归就是求解方程，拿一个最简单的例子来说就是对$y=kx+b$,只需要已知两个点$(x_1,y_1),(x_2,y_2)$就可以解得参数$k,b$.进而可以对其余点预测。也就是说你给我一个$x_n$,我可以带入方程预测$y_n$.这也就是我们常说的解方程。
但是，我们要清晰的认识到这只是理想的情况，现实中的数据错综复杂，仅仅依靠两个点根本不具有代表性，他们甚至存在偏差或者噪声（可以理解为假数据），因此，传统的机器学习对线性的回归的做法就不仅仅依靠两个点了。而是大量的数据点，这样又会带来一个问题，也就是说找不到一个直线方程来拟合这么多的点。因此，我们常常来要求求出的方程要尽可能的拟合所有的样本点，方程的预测和真实数据之间的误差就是所谓的损失值，才用梯度下降的方法可以不断的优化更新参数$k,b$.这里最终获得的方程不是“样本点的方程解”，应该叫“最优解”。这也就是线性回归的最通俗的理解。这里简单说下回归和分类的区别，回归一般值线性回归，预测值是一个连续值，也就是有小数点，而分类一般指逻辑回归。即把预测值应用激活函数划分，结果是一个离散的值。比如就西瓜数据集来说，回归可以是预测西瓜的含糖量，而分类就是根据含糖量划分好瓜坏瓜。

1.2 基本形式

给定由d个属性描述的示例$\text{x}=(x_1;x_2;...;x_d)$,其中$x_i$是第i个属性上的取值（这里的x代表一个上文中的一个点，而x本身可以具有很多的值，正如西瓜集中的根蒂，纹理，敲声。y代表标签或者说是真实值，也就是好瓜坏瓜。最后也就是找到参数$k,b$），而这里把问题一般化了，也就是x有d个属性，那么就需要d个参数w（这里用w代替k ，其实仅仅是名字不同而已）来拟合数据。专业来说就是线性模型试图通过属性的线性组合来进行预测的函数，即
$$f(x)=w_1{x}_1+w_2{x}_2+...+w_d{x}_d+b$$
一般的用向量形式写成
$$f(x)=w^{T}x+b$$
其中$w=(w_1;w_2;...w_d)$,w和b学得以后，模型就得以确定

1.3 公式推导——最小二乘法

就1.1中提到的机器学习为了使得模型更具泛化能力，要求方程学习更多的的样本，而且要求方程尽可能多的拟合被提供的数据，那么求出这样一些未知参数使得样本点和拟合线的总误差（距离）最小，而这个误差（距离）可以直接相减，但是直接相减会有正有负，相互抵消了，所以就用差的平方或者差的绝对值来计算。（而差的绝对值部分点不可导，因此一般我们采用差的平方来用作损失函数），那么对于拟合方程有$y=kx+b$ .为了便于我们更好的理解，我们下面纤细的推到以下这个过程。
现在假设我们找到了最佳拟合的直线方程$y=kx+b$
那么对于每一个样本点$x^{(i)}$,根据我们的直线方程，预测值为${\hat{y}}^{(i)}$可以表示为${\hat{y}}^{(i)}=k{x}^{(i)}+b$,真实值我们称作$y^{(i)}$.希望y^{(i)}和${\hat{y}}^{(i)}$的差距尽可能地小，那么用差的平方考虑所有样本表示为${\sum }_{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2$
那么我们的目标就是使得${\sum }_{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2$尽可能地小。而且${\hat{y}}^{(i)}=k{x}^{(i)}+b$,也即是说找到k和b，使得$J(k,b)={\sum }_{i=1}^m(y^{(i)}-k{x}^{(i)}-b{)}^2$尽可能小。这个式子也叫损失函数（loss function）。机器学习最终的优化过程就是优化参数使得问题的损失函数最小。这里先给出问题的解。
$$\begin{array}{rl}k& =\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m(x^{(i)}-\overline{x}{)}^2}\\ b& =\overline{y}-k\overline{x}\end{array}$$
对于$J(k,b)$分别对k和b求偏导，令偏导数等于零，也就是说求函数的最小值$
这里涉及到比较基础的数学计算，如下所示。
对b，有$\frac{\partial J(k,b)}{\partial b}=0$
$$\begin{array}{rl}\frac{\partial J(k,b)}{\partial b}& =\sum _{i=1}^{m}2(y^{(i)}-k{x}^{(i)}-b)(-1)=0\\ \sum _{i=1}^m(y^{(i)}-k{x}^{(i)}-b)& =0\\ \sum _{i=1}^m(y^{(i)}-k{x}^{(i)}-b)& =0\\ \sum _{i=1}^m{y}^{(i)}-k\sum _{i=1}^m{x}^{(i)}-\sum _{i=1}^{m}b& =0\\ \sum _{i=1}^m{y}^{(i)}-k\sum _{i=1}^m{x}^{(i)}-mb& =0\\ mb& =\sum _{i=1}^m{y}^{(i)}-k\sum _{i=1}^m{x}^{(i)}\\ b& =\overline{y}-k\overline{x}\end{array}$$
对k，由$b=\overline{y}-k\overline{x}和\frac{\partial J(k,b)}{\partial k}=0$
$$\begin{array}{rl}\frac{\partial J(k,b)}{\partial k}=\sum _{i=1}^{m}2(y^{(i)}-k{x}^{(i)}-b)(-x^{(i)})=0& \\ \sum _{i=1}^m(y^{(i)}-k{x}^{(i)}-b)x^{(i)}& =0\\ 展开整理可得\sum _{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})-k\sum _{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)})& =0\\ 解得k=\frac{{\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})}{{\sum }_{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)})}& \\ 这里涉及到一些等式的代换& \\ \sum _{i=1}^m{x}^{(i)}\overline{y}=\overline{y}\sum _{i=1}^m{x}^{(i)}=m\overline{y}\overline{x}=\overline{x}\sum _{i=1}^m{y}^{(i)}=\sum _{i=1}^m\overline{x}\cdot \overline{y}& \end{array}$$
那么对于k的结果进一步化简
$$\begin{array}{rl}k& =\frac{{\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})}{{\sum }_{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)})}\\ & =\frac{{\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y}-\overline{x}{y}^{(i)}+\overline{x}\cdot \overline{y})}{{\sum }_{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)}-\overline{x}{x}^{(i)}+{\overline{x}}^2)}\\ & =\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m(x^{(i)}-\overline{x}{)}^2}\end{array}$$
可以看到数学的结果“美”的，但是这个过程就一言难尽，所以说AI的尽头还是数学。又跑题了，上述这个过程就是著名的最小二乘法。这也可以说是线性回归的基础。也可以说是AI的起点。

1.4 多元线性回归

上述只有参数k和b，那么对于更多的参数应该怎么做呢？而且，要在计算机写程序就要求运算速度，那么就注定要用矩阵运算来求解。因此GPU（图形处理器）应运而生，适应于矩阵运算。这也是机器学习发展面临的最实际的问题，运算速度与多维特征。
下面我们就简单介绍一下求解的算法。首先如果采用矩阵运算的方式，就需要消除掉偏置b的影响，将他加入到矩阵运算中。求解的原理也很简单，我们把b设为$k_0$,其对应的特征$x$全为1（这样的矩阵在线性代数里被称作增广矩阵），这样可以随着特征矩阵X一起计算，改进后的向量$\hat{k}=(b;k)$（这里的k是多个参数的）也就是说k的他们总体。更确切地说$\hat{k}=(b,k_1,k_2,...,k_d)$那么对于由所有样本组成的特征矩阵为：

$$\left(\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_{1d}\\ 1& x_{21}& x_{22}& \cdots & x_{2d}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_{m1}& x_{m2}& \cdots & x_{md}\end{array}\right)=\left(\begin{array}{cc}1& x_1\\ 1& x_2\\ ⋮& ⋮\\ 1& x_m\end{array}\right)$$
其实全为1的一列，加入左侧右侧都是一样的，只不过最终的结果不同，当前的矩阵最终运算的参数第一个参数是偏置b，而当全为1的一列放入最右侧一列时，最后一个参数时偏置b。这样预测的结果$\hat{y}=X{\hat{k}}^T$,这里注意矩阵的运算要求第一个的矩阵的列等于第二个矩阵的行，这里X时m行d+1列，$\hat{k}$是1行，d+1列，所以要把$\hat{k}$转置。最终就是要优化$\hat{k}$了。
我们把最优化的${\hat{k}}^{\ast }=argmin(y-X\hat{k}{)}^T(y-X\hat{k}))$,那么我们损失函数$J(\hat{k})=(y-X\hat{k}{)}^T(y-X\hat{k}))$
$$\begin{array}{rl}\frac{\partial J(\hat{k})}{\partial \hat{k}}& =\frac{\partial (y-X\hat{k}{)}^T(y-X\hat{k})}{\partial \hat{k}}\\ & =\frac{\partial (y^{T}y-\hat{k}{X}^{T}y-y^{T}X\hat{k}+{\hat{k}}^T{X}^{T}X)}{\partial \hat{k}}\\ & =0-X^{T}y-X^{T}y+(X^{T}X+X^{T}X)\hat{k}\\ & =2X^T(X\hat{k}-y)\end{array}$$
这里的求解用到两个公式
$$\begin{array}{r}\frac{\partial {\alpha }^{T}x}{\partial x}=\frac{\partial x^T\alpha }{\partial x}=\alpha \\ \frac{\partial x^{T}Ax}{\partial x}=(A+A^T)x\end{array}$$
令$2X^T(X\hat{k}-y)=0$解得$\hat{k}=(X^{T}X{)}^{-1}{X}^{T}y$
但是我们必须清晰的认识到，这样的解只有在$(X^{T}X)$可逆才可以求解，而在实际任务中，往往样本数量会小于特征个数d，此时显然$(X^{T}X)$不满秩（这个是线性代数的专有名词，也就是不可逆），此时会有很多的$\hat{k}$满足方程。也就是解不唯一，我们的目的就是为了找到方程的最优解。那么常用的方法就是引入正则化项，进而对模型的参数设施限制。正则化项一般直接加入损失函数，称为损失函数的一部分，这样正则化项也会被当作优化项，也就是模型的参数不可以过大，这样就可以有效的抑制模型的表现力，限制模型变得复杂，也就是模型会变得更加简单，这将会提高模型的泛化能力，有效抑制模型的过拟合。而常见的正则化项由L1范数（也就是模型参数的绝对值，优化后使得参数向量稀疏）和L2范数（模型参数平方和开根号，使得向量二维范数降低）。
那么上述的问题该如何解决呢，梯度下降法给出了一个相对不错的答案，而梯度下降法因为对该问题的有效求解，当之无愧的称为AI界基石，也就是说几乎所有的模型参数的优化都离不开梯度下降的影子。关于梯度下降的详细过程我之前的博客由详细的描述，感兴趣的朋友可以点这里梯度下降算法
此外，还有一系列的方法对线性回归变式，比如再加入一个非线性的映射，使得模型含有非线性关系，比如$lny$.这样如果数据分布本身是$e^{kx+b}$的分布，加入非线性映射$lny$后，便成了我熟悉的线性回归。

二、逻辑回归理论总结

2.1 通俗理解

说到逻辑回归，不得不提到分类，提到分类就不得不说到一个东西，叫做激活函数。毕竟目前的AI都是基于统计学习方法，因此很依赖概率统计，我们需要一个方法，把预测的值转化到（0，1）的数，最好还是增函数，这样也很容易比较。最好还要可导。嘻嘻，是不是感觉要求这么多能找到吗？答案是肯定的，这个函数就是著名的sigmoid函数。它不仅在逻辑回归中占据重要地位，甚至目前大红大紫火的深度学习都离不开他的影子，它可以把线性的方法非线性化。使得深度神经网络理论上可以拟合任何的函数。
咳咳，扯得有点多。下面有请我们的主角登场，瞪灯等等，在哪里呢，看下图。

sigmoid：还有谁？还有谁？
哈哈，大哥直到现在都可以被称为是经典的激活函数，AI界的宠儿。仔细观察，他成功的把从$(-\infty ,+\infty )$的所有数都映射到了$(0,1)$,而且还是单调递增，而且还是处处可导。笔者只想说一句666。
来人把大哥的表达式请上来，$Sigmoid(x)=\frac{1}{1+e^{-x}}$.
这其实也就是逻辑回归的全部秘密。就是由于大哥的存在，回归就成为了分类，我们可以在其中设置一个阈值，一般是0.5，即大于0.5的为正类，小于0.5的为负类。另一个方面，逻辑回归的损失函数和线性回归的损失函数也有所区别。比如二分类的损失函数是二类交叉熵函数。
$$binaryCrossEntropy=-ylnp-(1-y)ln(1-p)$$

2.2 理论分析

对于激活后的结果为$$y=\frac{1}{1+e^{-(k^{T}x+b)}}$$
两边取ln对数有
$$\begin{array}{rl}y(1+e^{-(k^{T}x+b)})& =1\\ e^{-(k^{T}x+b)}& =\frac{1-y}{y}\\ -(k^{T}x+b)& =ln(\frac{1-y}{y})\\ k^{T}x+b& =ln(\frac{1-y}{y}{)}^{-1}\\ k^{T}x+b& =ln(\frac{y}{1-y})\end{array}$$
这里将y视作样本为正例的可能性，则1-y为样本为负例，两者的比值$\frac{y}{1-y}$称为几率（odds),表示是正例的相对可能性，对几率取对数可以得到对数几率，因此线性回归的结果去逼近是对数几率。逻辑回归其实本质上是一个分类模型。这样多分类的方法基本和二分类类似，方法有一对一，一对余，多余多。

2.3 类别分布不平衡

这里存在一个比较经典的例子，我想要设置一个分类器，帮助我找到癌症病人，可以想象数据分布中大致1000人有1人是癌症，那么如果以此为训练集，模型很容易认为基本上都是正常，准确率高达99.9%，但是，这个模型根本没有存在的意义。因此为了避免这种问题，尤其是在二分类的情况下，我们常常把正负样本的比例设置为1:1,并且为了排除顺序的干扰（前半部分都是正例，后半部分都是负例）。我们常常把样本集打乱顺序。
但是对于数据分布本身就存在问题的，我们也需要优化样本类别的方法。
（1）再放缩（rescaling）：主要思想是更改决策阈值，使之更加贴合正负样本的比例，比如我们设置阈值为0.1，也就是说只有预测小于0.1才被判定为患有癌症。
（2）采样（sampling）：对于多数样本欠采样，也就是少取点，对于少数样本过采样，也就是多取点，这样保证正负样本个数平衡。

三、代码实现

3.1 线性回归

**利用求解公式$\hat{k}=(X^{T}X{)}^{-1}{X}^{T}y$**求解参数

# ！/usr/bin/env python
# @Time:2022/3/22 16:02
# @Author:华阳
# @File:linear_regression.py
# @Software:PyCharm

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("ex0_1.csv",header=None)
data = df.values
X=data[:,0].reshape((-1,1))
Y=data[:,1].reshape((-1,1))
plt.scatter(X,Y)
x_min = min(X)
x_max = max(X)
ones=np.ones((X.shape[0],1))
X=np.hstack((ones,X))
XT=X.T
XTX=np.dot(XT,X)
XTX_1=np.linalg.inv(XTX)
XTX_1XT=np.dot(XTX_1,XT)
W=np.dot(XTX_1XT,Y)
x_w = np.linspace(x_min,x_max,100)
y_w = x_w*W[1]+W[0]
plt.plot(x_w,y_w)
plt.show()

运行结果：

线性回归案例:拟合学习时间和学习成绩关系(jupyter)：

1. 提出问题 已知一部分学生的学习时间和分数，预测另一部分学生的分数。其中，特征为学习时间，标签为分数。
2. 理解数据 将数据集导入python，计算相关系数
3. 构建模型 (1) 提取特征和标签 (2) 建立训练数据和测试数据 (3) 训练模型（使用训练数据） (4) 模型评估（使用测试数据）

#OrderedDict,实现了对字典对象中元素的排序。
from collections import OrderedDict
import pandas as pd
#建立数据集
examDict={
    '学习时间':[0.50,0.75,1.00,1.25,1.50,1.75,1.75,2.00,2.25,
            2.50,2.75,3.00,3.25,3.50,4.00,4.25,4.50,4.75,5.00,5.50],
    '分数':[10,  22,  13,  43,  20,  22,  33,  50,  62,  
              48,  55,  75,  62,  73,  81,  76,  64,  82,  90,  93]}
examOrderDict=OrderedDict(examDict)
examDf=pd.DataFrame(examOrderDict)
#查看数据集前5行
examDf.head()

#提取特征和标签
#特征features
exam_X=examDf.loc[:,'学习时间']
#标签labes
exam_Y=examDf.loc[:,'分数']
#绘制散点图
import matplotlib.pyplot as plt
#散点图
plt.scatter(exam_X, exam_Y, color="b", label="exam data")
#添加图标标签
plt.xlabel("Hours")
plt.ylabel("Pass")
#显示图像
plt.show()

#相关系数：corr返回结果是一个数据框，存放的是相关系数矩阵（协方差）
rDf=examDf.corr()
print('相关系数矩阵：')
rDf

#特征features
exam_X=examDf.loc[:,'学习时间']
#标签labes
exam_Y=examDf.loc[:,'分数']
from sklearn.model_selection import train_test_split
#建立训练数据和测试数据
X_train , X_test , Y_train , Y_test = train_test_split(exam_X,exam_Y,train_size=0.8)
#输出数据大小
print('原始数据特征：',exam_X.shape,'训练数据特征：',X_train.shape,'，测试数据特征：',X_test.shape)
print('原始数据标签：',exam_Y.shape,'训练数据标签：',Y_train.shape ,'测试数据标签：',Y_test.shape)
#散点图
plt.scatter(X_train, Y_train, color="blue", label="train data")
plt.scatter(X_test, Y_test, color="red", label="test data")

原始数据特征： (20,) 训练数据特征： (16,) ，测试数据特征： (4,)
原始数据标签： (20,) 训练数据标签： (16,) 测试数据标签： (4,)

#将训练数据特征转换成二维数组XX行*1列
X_train=X_train.values.reshape(-1,1)
#将测试数据特征转换成二维数组行数*1列
X_test=X_test.values.reshape(-1,1)
''' reshape(-1,列数)是根据所给的列数,自动按照原始数组的大小形成一个新的数组，
例如reshape(-1,1)就是改变成1列的数组，这个数组的长度是根据原始数组的大小来自动形成的。
reshape(行数,-1)是根据所给的行数，自动按照原始数组的大小形成一个新的数组。'''
#第1步：导入线性回归
from sklearn.linear_model import LinearRegression
#第2步：创建模型：线性回归
model = LinearRegression()
#第3步：训练模型
model.fit(X_train , Y_train)
'''
最佳拟合线：z= + x
截距intercept：a
回归系数：b
'''
#截距
a=model.intercept_
#回归系数
b=model.coef_
print('最佳拟合线：截距a=',a,'，回归系数b=',b)
#得到最佳拟合曲线： 
#训练数据散点图
plt.scatter(X_train, Y_train, color='blue', label="train data")
#训练数据的预测值
Y_train_pred = model.predict(X_train)
#绘制最佳拟合线
plt.plot(X_train, Y_train_pred, color='black', linewidth=3, label="best line")

最佳拟合线：截距a= 13.518458698661739 ，回归系数b= [15.04845408]

#线性回归的score方法得到的是决定系数R平方
model.score(X_test , Y_test)
#score内部会对第一个参数X_test用拟合曲线自动计算出y预测值，内容是决定系数R平方的计算过程。
#导入绘图包
import matplotlib.pyplot as plt
#第1步：绘制训练数据散点图
plt.scatter(X_train, Y_train, color='blue', label="train data")
#第2步：用训练数据绘制最佳线
#最佳拟合线训练数据的预测值
Y_train_pred = model.predict(X_train)
#绘制最佳拟合线：标签用的是训练数据的预测值y_train_pred
plt.plot(X_train, Y_train_pred, color='black', linewidth=3, label="best line")
#第3步：绘制测试数据的散点图
plt.scatter(X_test, Y_test, color='red', label="test data")
#添加图标标签
plt.legend(loc=2)
plt.xlabel("Hours")
plt.ylabel("Score")
#显示图像
plt.show()

案例分析二波士顿房价（pycharm)

# ！/usr/bin/env python
# @Time:2022/3/22 16:02
# @Author:华阳
# @File:linear_regression.py
# @Software:PyCharm

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.utils import shuffle
df = pd.read_csv("boston.csv")
df = np.array(df.values,ndmin=2)
x_data = df[:,:12]
#归一化
for i in range(12):
    x_data[:,i] = (x_data[:,i]-x_data[:,i].min())/(x_data[:,i].max()-x_data[:,i].min())
y_data = df[:,12]
#将后10个作为测试集，不参加训练
test_x = x_data[-10:]
test_y = y_data[-10:]

x_d = x_data[:-10]
y_d = y_data[:-10]
#初始化参数
w = np.random.normal(0.0,1.0,(1,12))
b = 0.0
#设置训练轮次
train_epochs = 200
learing_rate = 0.001
loss_=[]
for count in range(train_epochs):
    loss=[]
    for i in range(len(x_d)):
        re = w.dot(x_d[i])+b
        err_loss = (y_d[i]-re)*(y_d[i]-re)
        err = 2*(y_d[i]-re)
        w += learing_rate*err*x_d[i] #err种re为负值，所以没有负号
        b += learing_rate*err
        #记录误差
        loss.append(abs(err_loss))
    loss_.append(sum(loss)/len(loss))
    print("第%d轮次，损失值为：%.3f"%(count+1,sum(loss)/len(loss)))
    #随机打乱训练集中的样本，防止模型出现结果和输入的位置有关的情况
    x_d,y_d = shuffle(x_d,y_d)
#打印误差的变化情况
fig1 = plt.figure(1,(5,5))
plt.plot(loss_)
plt.show()
#简单的评估，看看实际值和预测值之间的误差
sum_loss = 0
for i in range(10):
    print("true:\t{}".format(test_y[i]),end="\t")
    pre = np.dot(w,test_x[i])+b
    sum_loss += (pre-test_y[i])**2
    print("guess:\t{}".format(pre))
pre = [np.dot(w,x_d[i])+b for i in range(len(x_d)-10)]
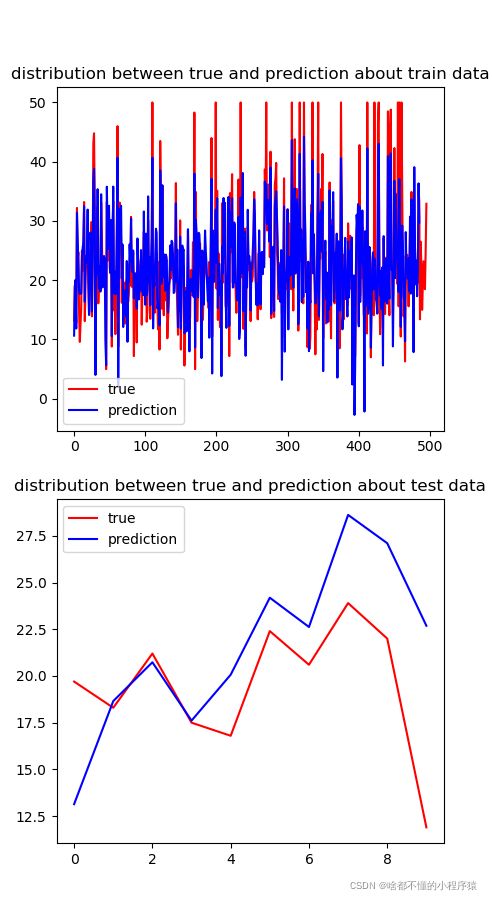
fig2 = plt.figure(1,(5,10))
axe_train = fig2.add_subplot(211)
axe_train.set_title('distribution between true and prediction about train data')
axe_train.plot(y_d,color='red',label='true')
axe_train.plot(pre,color='blue',label='prediction')
axe_train.legend()
pre1 = [np.dot(w,test_x[i])+b for i in range(len(test_x))]
axe_test = fig2.add_subplot(212)
axe_test.set_title('distribution between true and prediction about test data')
axe_test.plot(test_y,color='red',label='true')
axe_test.plot(pre1,color='blue',label='prediction')
axe_test.legend()

print("测试集损失为%.3f"%sum_loss)
plt.show()

3.2 逻辑回归

头歌案例一逻辑回归实现癌细胞识别
动手实现逻辑回归 - 癌细胞精准识别
数据集介绍
乳腺癌数据集，其实例数量是 569 ，实例中包括诊断类和属性，帮助预测的属性一共 30 个，各属性包括为 radius 半径（从中心到边缘上点的距离的平均值）， texture 纹理（灰度值的标准偏差）等等，类包括： WDBC-Malignant 恶性和 WDBC-Benign 良性。用数据集的 80% 作为训练集，数据集的 20% 作为测试集，训练集和测试集中都包括特征和类别。其中特征和类别均为数值类型，类别中 0 代表良性， 1 代表恶性。

# -*- coding: utf-8 -*-

import numpy as np
import warnings
warnings.filterwarnings("ignore")

def sigmoid(x):
    '''
    sigmoid函数
    :param x: 转换前的输入
    :return: 转换后的概率
    '''
    return 1/(1+np.exp(-x))


def fit(x,y,eta=1e-3,n_iters=10000):
    '''
    训练逻辑回归模型
    :param x: 训练集特征数据，类型为ndarray
    :param y: 训练集标签，类型为ndarray
    :param eta: 学习率，类型为float
    :param n_iters: 训练轮数，类型为int
    :return: 模型参数，类型为ndarray
    '''
    #   请在此添加实现代码   #
    #********** Begin *********#
    theta = np.ones((x.shape[1]+1,1))
    print(theta.shape)
    a = np.ones((len(x),1))
    X  = np.hstack([a,x])
    count = 0
    while(count < n_iters):
        predict = X.dot(theta)
        theta1 = theta - eta * (predict - y).dot(X)
        theta = theta1 
        count += 1
    return theta[1:]
    


    #********** End **********#

逻辑回归实现手写字识别
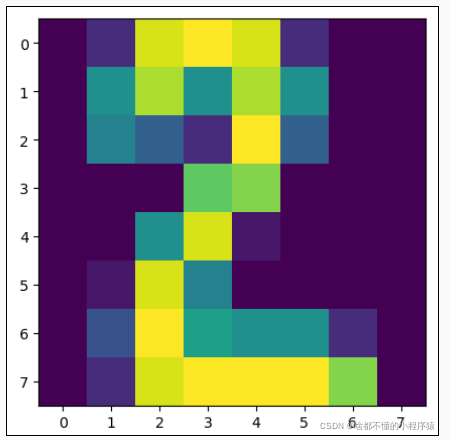
手写数字识别,本关使用的是手写数字数据集，该数据集有 1797 个样本，每个样本包括 8*8 像素（实际上是一条样本有 64 个特征，每个像素看成是一个特征，每个特征都是float类型的数值）的图像和一个 [0, 9] 整数的标签。比如下图的标签是 2 ：

方法一：调参比较麻烦

from sklearn.linear_model import LogisticRegression

def digit_predict(train_image, train_label, test_image):
    '''
    实现功能：训练模型并输出预测结果
    :param train_sample: 包含多条训练样本的样本集，类型为ndarray,shape为[-1, 8, 8]
    :param train_label: 包含多条训练样本标签的标签集，类型为ndarray
    :param test_sample: 包含多条测试样本的测试集，类型为ndarry
    :return: test_sample对应的预测标签
    '''

    #************* Begin ************#
    model = LogisticRegression(max_iter=500,C=0.3)
    train_image = train_image.reshape(-1,64)
    test_image = test_image.reshape(-1,64)
    model.fit(train_image,train_label)
    result = model.predict(test_image)
    return result
    #************* End **************#

方法二：对数据归一化

from sklearn.linear_model import LogisticRegression
def digit_predict(train_image, train_label, test_image):
    '''
    实现功能：训练模型并输出预测结果
    :param train_sample: 包含多条训练样本的样本集，类型为ndarray,shape为[-1, 8, 8]
    :param train_label: 包含多条训练样本标签的标签集，类型为ndarray
    :param test_sample: 包含多条测试样本的测试集，类型为ndarry
    :return: test_sample对应的预测标签
    '''
    #************* Begin ************#
    # 训练集变形
    flat_train_image = train_image.reshape((-1, 64))
    # 训练集标准化
    train_min = flat_train_image.min()
    train_max = flat_train_image.max()
    flat_train_image = (flat_train_image-train_min)/(train_max-train_min)
    # 测试集变形
    flat_test_image = test_image.reshape((-1, 64))
    # 测试集标准化
    test_min = flat_test_image.min()
    test_max = flat_test_image.max()
    flat_test_image = (flat_test_image - test_min) / (test_max - test_min)
    # 训练--预测
    rf = LogisticRegression(C=4.0)
    rf.fit(flat_train_image, train_label)
    return rf.predict(flat_test_image)
    #************* End **************#