运动模糊图像恢复处理-matlab实现

注：原问题来自第十一届数学中国数学建模网络挑战赛。

基于图像退化原理建立了线性复原系统，即退化模型，PSF 函数与图像数据卷积模拟出运动模糊的退化图像。由于在模糊图像复原问题中，PSF函数的求解至关重要，因此利用倒频谱估计出模糊图像的模糊方向和模糊范围的像素值,从而建立了PSF函数。最后针对图像复原问题,通过维纳滤波寻找一个合适的复原图像使得它与原始清晰图像之间的均方误差达到最小,从而得到一张能还原程度较高的复原图像。

---

在 matlab2017 软件上进行退化图像的仿真模拟：

1. 首先，选取一张尺寸为 600 x 537，分辨率为 300*291 的高清图片，

2. 对图片设定模糊长度以及模糊角度，

3. 利用 PSF 函数对图片进行模拟运动模糊处理，其效果图如下：

 

为了测试本章所提出的倒频谱估计法的估计精度，初步设想利用倒频谱算法对由标 准图计算机模拟仿真产生的一些模糊影像进行运动参数估计实验。值得注意的是，实验 中所采用的模拟模糊影像均是在假定影像不符合周期性条件下卷积得到的这与真实模 糊影像的产生条件一致。 由于具有对称性，测试的模糊影像的真实运动方向分布在测试的模糊影像的真实运 动方向分布在-90°~90°之间，真实的模糊范围像素值从 1 像素到 60 之间，在维纳滤 波的方法中我们提到不同 K 值会影像图片的还原程度，以下是由 K 值变化引起的效果：

运动模糊图

维纳滤波处理后的图像

取不同k值得到的效果 

 

 

恢复评价：

 

 

---

 

仿真处理（模糊图片）：

 g（x,y）=f(x,y)*h(x,y)+n(x,y)

g（x,y）为原始图像 f 和运动模糊函数点扩展函数 h 卷积后叠加加性噪声后的结果。 在忽略加性噪声条件下，复原图像到 f 即为一个逆向问题，需要估计系统中的点扩展函数（PSF） 参数。我们将基于倒频谱算法估计参数即模糊长度及模糊角度，这样我们就可以建立 PSF 函数，进 而用维纳滤波进行图像复原。

---

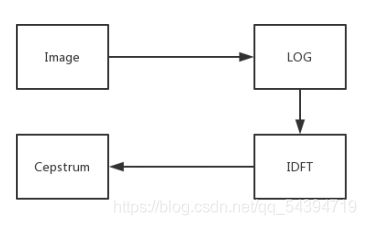
使用倒频谱算法

许多 PSF 参数估计方法主要采用基于傅立叶频谱的分析方法，利用模糊影像的频谱 在运动方向上存在的某些特征与运动参数存在的特征，检验特征，进而得到运动参数。 但是这种方法只能间接分析模糊参数，无法直接定量给出参数值，即无法自动识别参数， 需要人为辅助，多次尝试以或得结果。因此我们使用倒频谱算法：

即对一维信号 x(n)进行一维离散傅立叶变换为

推广到二维信号,在除噪情况下，简化模糊影像的傅立叶频谱可表达为 G（u,v）=O（u,v）H(u,v) 两边取绝对值后继续求取对数，得到：

 

做傅立叶反变换得到实数倒频谱为 

设倒频率自变量为 q,则上式可简写为：

由以上推导可知，在经过求取倒频谱的一系列过程，运动模糊过程在时域可以利用 o(x,y)和 h(x,y)的卷积表示，在频域则变成 O(x,y)与 H(x,y)的乘积关系；而在倒频域 则变成()与()的相加关系，这一转化过程使得在倒频域模糊系统的特性()与 原始影像特性()明显区别开来。 

 

---

维纳滤波

考虑对加性 噪声相对比较友好的最小均方差滤波即维纳滤波对含有噪声的模糊图像进行最大限度 的复原。

推导略

可以得到二维维纳滤波去卷积滤波器的传递函数为

 

 因为 噪声信息就位于 G 中，而 G 是已知的，但 Sf(u,v)确实无法估计的，因为 F 是未知的（也 正是我们所需要估计的）。因此，我们采用一个常数值 K 来代替参数 Sη(u,v)/Sf(u,v), 这时，K 就变成了一个可以调节的参数了，所以常用下面的式子来近似代替：

K 为一个常数，通过交互式地改变 K 和观察复原效果，实验就可以顺利的进行了。

---

图像清晰度评价算法

目前对于我们想要复原为清晰的运动模糊图像，我们可以通过一 种对运动模糊图像适应度很好，可以较好地描述清晰程度的算法，来用数值上的结果 反映，我们图像的模糊清晰程度。在这里，我们为了方便阐述，把这种算法称为，运 动模糊图清晰度算法。 算法流程图如下：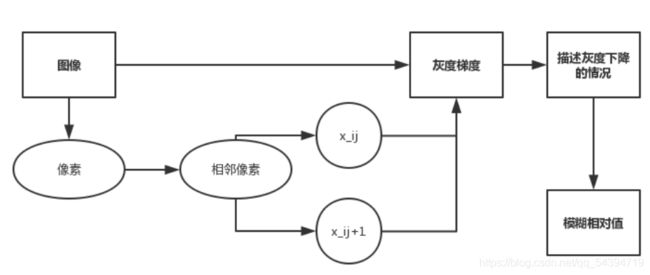 

算法原理如下：

1、以一张未知模糊程度（记分辨率为 m*n）的图片为例。我们将其每一个像素进 行灰度化处理。

2、通过灰度化处理的图像，每一个像素转化为其矩阵的元素，每一个元素的数值 对应于图像上灰度值。

3、我们希望通过像素与像素之间灰度值的变化的快慢来反映，灰度值下降的快慢 情况。如果灰度下降得快，表明在该像素与像素之间存在边缘刻画明显的现 象。如果灰度下降得慢，则表明该像素与像素之间边缘效果不明显，该小部分 区域较模糊。

4、通过对小区域像素的分析，我们希望将这个原理，反映到整个图像的处理上， 使得图像上全部像素的灰度值梯度变化，能够反映这张未知模糊程度的图片的 清晰模糊程度。这里我们用 k（斜率）来说明这一情况。

5、为了降低图像噪声，附加在灰度值上，在计算上可能会造成的影响。我们采用 隔列取像素做斜率的方法，将每一个斜率进行总和，再做平均到每个像素的斜率情况。 即

 6、同时值得注意的一点就是，当像素周围，灰度值相同的情况，很有可能不是边缘，所以应该排除这两像素间的斜率情况，即不能将这个情况算入，计算像素 总数 a。

7、最后取该图片多张模糊程度的图像，然后对他们 k 的值，进行相对比较化。 通过这种运动模糊图清晰度算法，我们可以对上述的维纳滤波处理后的图像做 出验证。我们已知多张 k（人为信噪比交互值）不同的维纳滤波处理图像，希望从 数值的角度，验证 k 越小，图像越清晰。

---

附录一：（退化处理）

I=imread('c.jpg');
len=20; theta=30;
PSF=fspecial('motion',len,theta); %建立二维线性运动函数 PSF
I1=imfilter(I,PSF,'circular','conv'); %对 HD 图 PSF 模糊处理
subplot(121);imshow(I);title('原图像');
subplot(122);imshow(I1);title('运动模糊处理后图像');

附录二（维纳滤波）

I2 = im2double(I1);
PSF = fspecial('motion', 20,30);
frest1 = deconvwnr(I2, PSF, 0.001);
subplot(121),imshow(I1); title('原模糊图像');
subplot(122),imshow(frest1); title('维纳滤波处理后图像');

附录三（randon 变换求解 PSF 参数估计）

I = imread('c.jpg');
figure
subplot(231),imshow(I);title('原图');
PSF = fspecial('motion',80, 150);
g = imfilter(I, PSF, 'circular');
subplot(232),imshow(g);title('运动模糊图');
gb = rgb2gray(g);
PQ = paddedsize(size(gb));
F = fft2(gb, PQ(1), PQ(2));
subplot(233),imshow(F); title('频谱图');
F1 = log(1+abs(F));
F2 = abs(F1).^2;
F3 = real(ifft2(F2));
subplot(234),imshow(F3); title('倒频谱');
H = log(1+abs(F3)); 
Hc = fftshift(H); 
T = graythresh(Hc);
bw=edge(Hc, 'canny', T);
subplot(235), imshow(bw);title('二值化倒频谱');
theta = 1:180;
R = radon(bw, theta);
subplot(236), imshow(R); title('radon 变换');
MAX = max(max(R));
[m, n] = find(R == MAX);
if 90 < n <= 180
 beita = n - 90;
else if 0 < n < 90
 beita = n + 90;
 else if n == [90;90] | n == [180;180]
 beita = n(1);
 end;

附录四（判别清晰度）

[n,m]=size(gb);
gb= rgb2gray(frest1);
a=0;
sum=0;
for j=1:3:m
for i=1:2:n
sum=sum+abs(gb(i,j)-gb(i,j+1))+abs(gb(i,j+1)-gb(i,j+2));
 if gb(i,j)~=gb(i,j+1)
 a=a+1;
 end
 if(gb(i,j+2)~=gb(i,j+1))
 a=a+1;
 end
end
end
S1=sum/a;
HDER=[S1 S2 S3 S4];
HDE=HDER/max(HDER);
plot(HDE);