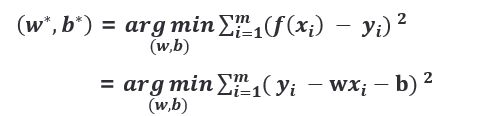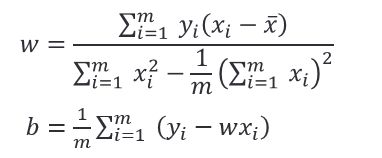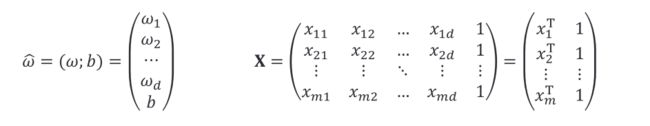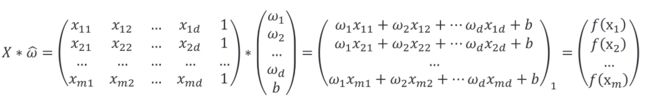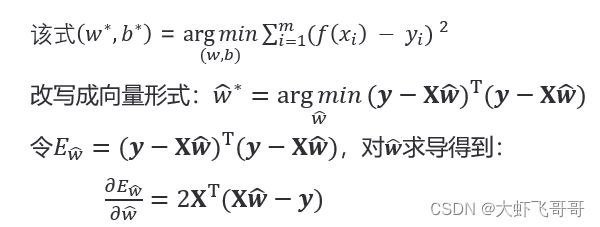机器学习-线性回归
机器学习-线性回归
- 一、线性回归概念
- 二、怎样求解回归系数
- 三、最小二乘法
- 四、多元线性回归
- 五、岭回归
- 六、Lasso回归
一、线性回归概念
首先举个例子,我们去市场买牛肉,一斤牛肉52块钱,两斤牛肉104块钱,三斤牛肉156块钱,以此类推。也是说牛肉的价格随着牛肉斤数的增加而有规律地增加,这种规律可以下图表示:
可以看到上述规律可以用一条直线来表述,这就是一个线性模型。用 y 表示牛肉斤数,用 $ $表示价格,就得到方程: = 52 =52 y=52x。这个方程就叫做回归方程,52叫做回归系数,求解回归系数的过程叫做回归。
线性回归首先假设自变量和因变量是线性关系,然后通过对现有样本进行回归,进而计算出回归系数以确定线性模型,最后使用这个模型对未知样本进行预测。
二、怎样求解回归系数
有这样一个数据集,很容易看出,这些数据是线性的,因此可以使用线性回归来拟合。由于每个样本点只有一个自变量和一个因变量,因此可以用如下回归方程来表示模型: ( ) = + ()=+ f(x)=wx+b
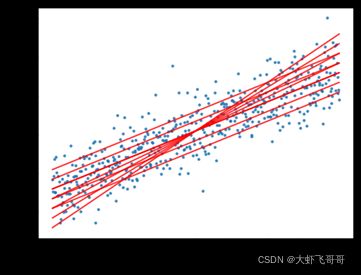
在图中画出几条通过样本集的直线,可以看到通过样本集的直线有无数条,每一条都由 w 和 b 确定。我们的任务就是找到那条最符合数据集的直线,也就是求得最优的 w 和 b。
如何计算最优的 和 ?最常用的方法:最小二乘法。
三、最小二乘法
对于数据集中不同的点,我们试图学到:
( ) = + (_ )=_+ f(xi)=wxi+b,使得 ( i ) ≈ (_i )≈_ f(xi)≈yi( _ yi 为真实值)
如何计算最优的 和 ,关键在于如何衡量 () 与 y 之间的差别。最小二乘法就是试图找到一条直线,使所有样本到直线的欧式距离之和最小。欧式距离与均方误差相对应,即:
求解 和 的过程,称为线性回归模型的最小二乘“参数估计”。
将 ( , ) _{(,) } E(w,b) 分别对 和 求导,得到:
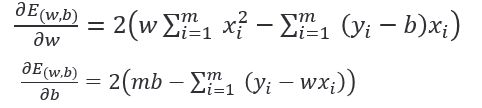
令两式为零,可得到 和 的最优解:
四、多元线性回归
上面所述,一个属性对应一个输出的求解过程,接下来,我们讨论当有多个属性的求解过程。给定由d个属性描述的示例表示为: = ( 1 ; 2 ; … ; ) , ( ) = + =(_1;_2;…;_ ), ()=+ x=(x1;x2;…;xd),f(x)=wx+b 需要改写成:
( ) = 1 1 + 2 2 + … + + ()=_1 _1+_2 _2+…+_ _+ f(x)=w1x1+w2x2+…+wdxd+b
一般向量形式: ( ) = T + ()=^T + f(x)=wTx+b
对于样本由个属性描述的数据集,我们试图学得: ( ) = T + , 使 得 ( ) ≈ ()=^T +,使得 (_ )≈_ f(x)=wTx+b,使得f(xi)≈yi ,这称为多元线性回归。将具有m个样本的数据集表示成矩阵X,将系数 w 与 b 合并成一个列向量,这样每个样本的预测值以及所有样本的均方误差最小化就可以写成下面的形式:
令上式为零可求得 w ̂的最优解。求解过程中,对矩阵进行讨论,只有 T ^T XTX 为满秩时,求得最优解:
![]()
![]()
五、岭回归
上述我们提到,线性回归模型中 X T X X^T X XTX往往不是满秩矩阵。有以下两种情况:
(1)数据集的列(特征)数量 > 数据量(行数量),即 X 不是列满秩。
(2)数据集列(特征)数据之间存在较强的线性相关性,即模型容易出现过拟合。
此时,可以解出多个回归参数,使得均方误差最小化。我们选择哪一个解作为输出,将由学习算法的归纳偏好决定,常见的做法就是引入正则化项。
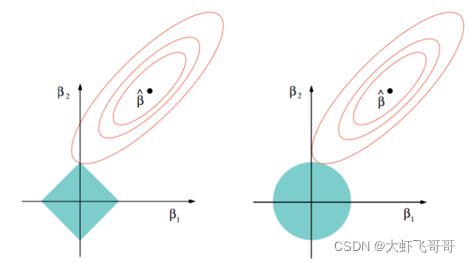
岭回归应运而生,岭回归可以被看作为一种改良后的最小二乘法,它通过向损失中添加 L 2 L_2 L2正则项(2-范数)有效防止模型出现过拟合,且有助于解决非满秩条件下求逆困难的问题,从而提升模型的解释能力。
在普通最小二乘法加上 L 2 L_2 L2 正则项就是岭回归:
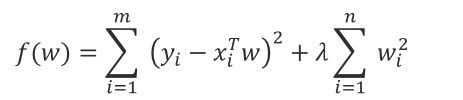
通过加入此项进行优化后,限制了回归系数 _^ 的绝对值,数学上可以证明上式的等价形式如下:
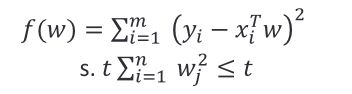
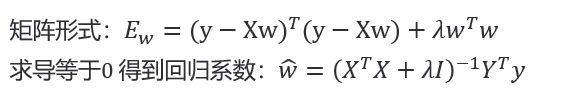
假设 w 是一维的,显然 ∑ = 1 m ( − ) 2 {∑^m_{=1}} (_−_^ )^2 ∑i=1m(yi−xiTw)2 这是一个元二次函数,如右图蓝色曲线所示,最小值点就是所求的 w w w; ∑ = 1 m 2 {∑^m_{=1}} _^2 ∑i=1m wi2 这一项是经过原点的二次函数,如图红色曲线所示。
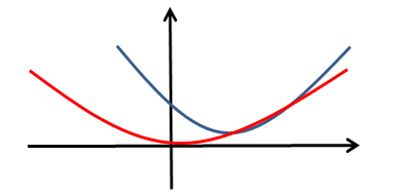
给定一个平衡的常数 λ λ λ,将两者相加(用绿色的线表示),如图所示。 λ λ λ 越大, w 取值越接近于 0。
六、Lasso回归
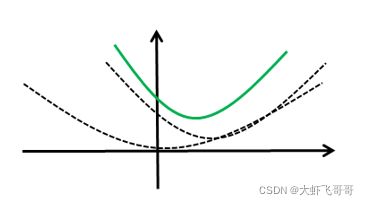
在普通最小二乘法加上 L 1 L_1 L1 正则项就是 L a s s o Lasso Lasso 回归:
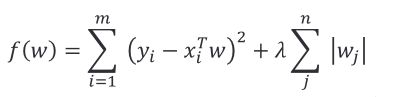
L a s s o Lasso Lasso 回归和岭回归,最大的区别是,通过缩减,可以使某些特征值的权重为零,即无关项。