计算机组成原理 第二章 数据的表示与运算
第二章主要是一些有关计算机内部的计算的知识,还包括计算机数据的存储,重点在于计算的方法。
2.1数制与编码
计算机内采用二进制进行编码,这样做的原因有:
①二进制只有0和1两种状态,正好与计算机内的高低电平相对应
②二进制位的0和1刚好与真和假对应,便于逻辑判断
③二进制的编码和运算规则都很简单,能通过逻辑门电路方便的实现运算

几种进制之间转换只需要对好位即可,其中十进制与二进制之间的转换是重点,其余可以基于二进制来转换。
十进制转二进制时,整数部分用除法,不断除二取余,最后逆序,小数部分则采用乘二取整。具体例子如下:

这个例子中,先把十进制拆成整数部分和小数部分,整数部分不断做除法,最后逆序,得到的就是整数部分的二进制形式,也可以进行拆分,将十进制数拆成几个二的幂次的和的形式,在对应改写成01形式,小数部分是不断乘二,大于1则把1取出来继续乘,直到变成零,同理也可以把小数部分拆成二的幂次的和形式,但是二的负数次方一般不好记,所以多用不断乘法的方法。
从十进制转二进制的过程不难看出,并不是每个十进制小数都有对应的二进制表示形式,如果在做乘法的过程中没有出现乘积为1.000的形式,那么这个乘法是在一直进行的,也就是无限循环的,所以没有对应的表示形式。
十进制转二进制是最难的一步,其余的转换就简单很多了。二进制转十进制只需要对应乘以二的多少次幂然后求和。
![]()
这两个进制之间的转换是最重要的,其余的进制都通过二进制作为跳板。二进制转八进制时,只需要将二进制的表示从右向左三个一位写成对应的八进制形式。二进制转十六进制则是四个一位做对应,两种转换在位数不够时,都采用高位补零的方法。

数据在计算机内部的存储涉及以下的几个概念:
真值:机器数所代表的真实值,即现实中人类所使用的值。
机器数:由于符号无法在计算机内表示,所以在编码时需要将符号也编为数字,这种把符号位编成数字的数称为机器数。
所以,真值就是实际的数值,而机器数是编码进入计算机之后的数值。
二进制编码的十进制数通常采用思维二进制来表示一位十进制中的数,而四位二进制可以表示16个十进制数,所以必然会有6个多余。常用的编码方式有以下三种(最重要的是第一种):
①BCD码
最常用的一种,四位二进制从右到左分别是1、2、4、8,转换时按照对应位数乘起来相加即可。两个8421码相加时如果和小于1101是不需要修正的,但大于等于1001时就需要修正,本质原因是两个8421码相加如果超过1001,相当于十进制的数相加超过了9,需要进位,而8421码可以多表示6个码,会出现进位上的差异,所以采用加6修正的方法,即运算结果上加六并向高位进位。

②余3码
这是一种无权码,是在 8421 码的基础上加0011形成的,因每个数都多余3,因此称为余3码。如8对应1011,9对应1100。
③2421码
这也是一种有权码,权值由高到低分别为 2、4、2、1 ,特点是大于等于5的4位二进制数中最高位为1,小于5的最高位为0。如 5对应1011 而非 0101 。
除此之外,计算机内还有校验码来发现纠正错误。校验码都是通过增加一些冗余码来检查或者纠错。任意两个合法码字之间最少变化的二进制位数称为校验码的码距,码距不小于2的数据校验码开始具有检错能力,码距越大,检错和纠错能力就越强,而且检错能力一直是小于纠错能力的。码距的概念比较抽象,这里举个例子:1100和1101之间的码距就是1,因为只有最后一位是不一样的,1001和0010直接的码距则是3,因为除了第二位都是变化了的。可以说码距就是任意两个合法码字之间对应位置不同的位的个数。
常用的校验码有三种:
①奇偶校验码
在原码上增加一个校验位,使其可以检测出一位错误,但不能确定出错的位数,也不能检测出偶数位的错误。基本方法是补上一位,使得整个码里面的0或1的个数为奇数或者偶数,当为偶数时为偶校验,奇数时为奇校验。这种校验方法具有局限性,只有奇数位出错时才能检验出来,而有偶数个位数出错时则检验不出来。但是按照计算机网络里面提到的,实际使用这种校验方法时,两位同时出错的概率很小,基本可以忽略。
②汉明码
其实现原理是在有效信息位中加入几个校验码形成海明码,是一种多重奇偶校验码。重点要掌握其编码的方法。


求海明码的过程一共有四步:确定位数-确定分布-分组确定校验关系-给校验位赋值。其中位数需要用公式来确定,确定好后,海明码校验位放在1 2 4 8 等二的幂次位上,其余位依次放数据,之后根据例题中的画法将数据位分组,分组主要是看数据所在的位置的号码可以由那几个校验码所在位置的号码加起来得到。确定好分组后,校验位根据分组结果进行异或(相同为0相异为1)即可。
检验是否出错则需要数据校验位一起判断,根据组对应做异或,结果如果不是0说明有错,而且这个数对应的十进制就是出错的位号。
③CRC循环冗余校验码
计算机网络里面的老料了,这里简单提一下。根据信息的长度移位,原信息如果是n位,就左移n-1位,后面是0,拿原本信息去除校验码,余数补到最后的几位上即可。
2.2定点数的表示方法
计算机内参与运算的数分为有符号数和无符号数两类。无符号数即没有符号位,所有的二进制数位都是数值位,相当于数的绝对值,由于其没有符号位,所以如果机器字长是8位,那么表示的数的范围可以达到0-255。与之对应的是有符号数,约定最高位为符号位,1表示负0表示正,拿出一位来表示符号的代价就是表示范围发生了变化,变为-127~127。
计算机内根据符号位是否固定分为定点数和浮点数,定点数即约定机器数中的小数点的位置是不变的,小数点要么在数据最高位之前,要么在数据最低位之后,并将前者称为定点小数,将后者称为定点整数。所以定点小数是纯小数,定点整数是纯整数。
定点小数的表示如下图:

符号位在小数点之前,不难发现当x0=0且后面所有位全为1时表示的就是最大的正数,当x0=1且后面所有位全为1时为最小的负数。
定点整数的表示如下图所示:

与定点小数同理,符号位为0其余全为1表示最大正数,符号位为1其余全为1表示最小负数。
计算机内有四种编码:原码、补码、反码、移码
①原码
即用最高位表示符号其余表示数值。是最基础的一种编码。
原码中有两个0,这是因为符号位的原因,+0用原码表示是00000000而-0用原码表示则是10000000,两者实际上是不同的。
②补码
补码主要是为了解决原码运算时过于复杂的问题,用补码可以很好的解决减法计算的问题。不论小数还是整数的补码,其变化方式都为:正数的补码是自己,负数的补码除符号位取反再在末尾加一。计算机内部的定点数都采用补码的形式进行存储(浮点数并不采用这种方式存储)。
补码中只有一个零,+0和-0是一样的,空出来的10000000人为规定表示小数表示-1整数表示-128。所以对于八位补码,整数的表示范围为-128~127。
③反码
反码多用作求补码过程中的中间步骤,即除符号位之外取反。反码中也有两个0。进行二进制运算时常用到有X补求(-X)补,这种情况下让X带着符号位取反之后在末位加一即可。
④移码
移码就是在真值的基础上都加一个固定的数,相当于对数进行了偏移。这个增加的数可以是任何数,这个数成为移码的偏置值,一般默认是加最高位为1其余位为0对应的二进制数。
移码中只有一个零,移码全零时表示的不是0而是要减去移码加上去的偏置值,移码保持了数据原有的大小顺序,由于都同时加上了相等的数,所以真值大的移码依然是大的。
定点数在运算时,主要有以下几种运算:
①定点数移位运算
移位运算分为算术移位、逻辑移位和循环位移。算术移位的对象是有符号数,移动过程符号位保持不变,移动过程的补充如下图:

对于原码,左移如果不溢出,则相当于对真值做了一次乘二,右移如果不考虑舍弃的位数,则相当于做了一次除二。
逻辑移位则是将数视为无符号数,连带符号位一起进行移动。逻辑左移高位丢失低位补0,逻辑右移低位丢失高位补0,注意逻辑移位只有补0这一种补法。
循环位移则是进行大循环,理解好图中的几种循环方式即可。正是这种循环的操作,使得循环位移更适合数据的低字节和高字节进行数据互换。具体见下图:

②原码定点数加减法
加法规则:先判符号位,若相同,则绝对值相加,结果符号位不变; 若不同, 则做减法,绝对值大的数减去绝对值小的数,结果符号位与绝对值大的数相同。
减法规则:两个原码表示的数相减,首先将减数符号取反,然后将被减数与符号取反后的减数按原码加法进行运算。
③补码定点数加减法
计算机内普遍采用补码进行加减运算。
计算过程中两个操作数均使用补码表示,从低位开始向高位移动并一位一位做加法运算,最后和只保留原来位数的长度。如果是加法则直接相加,如果是减法则将被减数与减数的机器负数相加。
④符号扩展
符号扩展也可以看作是对齐,比如一个8位二进制和一个32位二进制相加,不能让32位变成8位,只能让8位补充位数从而变成32位。
正数的符号扩展非常简单,即原有形式的符号位移动到新形式的符号位上,新表示形式的所有附加位都用 0 进行填充。
负数的符号扩展方法则根据机器数的不同而不同。 原码表示负数的符号扩展方法与正数相同, 只不过此时符号位为 1。 补码表示负数的符号扩展方法:原有形式的符号位移动到新形式的符号位上, 新表示形式的所有附加位都用 1(对于整数)或 0 (对于小数)进行填充。 反码表示负数的符号扩展方法:原有形式的符号位移动到新形式的符号位上,新表示形式的所有附加位都用1进行填充。
⑤溢出的判断
溢出是指运算结果超过了数的表示范围。通常,称大于机器所能表示的最大正数为上溢,称小于机器所能表示的最小负数为下溢。仅当两个符号相同的数相加或两个符号相异的数相减才可能产生溢出,如两个正数相加,而 结果的符号位却为1(结果为负);一个负数减去一个正数,结果的符号位却为0(结果为正)。定点数运算出现溢出时,运算结果是错误的。
判断溢出是一个很重要的知识点。主要有三种方法
a 一位符号位
只要运算前后符号位不发生变化就没有溢出,如果运算前后符号位反了,说明是因为溢出导致的。
b 两位符号位
双符号位也称模4补码,运算结果的两个符号位相同表示没有溢出,两个符号位不同则表示溢出了。两个符号位高位表示真正的符号,其中两个符号位的组合分别表示不同的意思:

c 采用一位符号位根据数据位进位来判断
本质上就是一位符号位的一种变形,如果进位的位与最高位相同,则没有溢出,否则就溢出了。实际上是一样的,最高位如果和进位位相同,那么进位之后会再次在符号位上进位,从而产生溢出。第三种方法实际上就是第一种的变形。
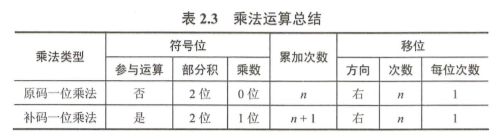
⑥定点数的乘法
计算机内部的乘法运算是由累加和右移来实现的。
a原码一位乘法
数值位与符号位分开计算,符号位异或形成,而数值位取其绝对值做乘法运算。
二进制的乘法是个很抽象的过程,一定要结合例题去计算,掌握好计算的过程。

计算过程有这么几个要点,首先部分积取两位符号位,初始状态为00,每次加的数为乘法表达式中前面的数,将乘法表达式中后面的数写在后面,末位为0则只右移,末位为1则在部分积中加上乘法表达式中前面的数再右移,多出去的位丢弃,重复操作直到后面的数全部移出去,结果就是乘积的绝对值部分。再将符号位补上,得到的就是乘法计算的结果。
b补码一位乘法
这种运算是根据末位和补充的最低位来进行计算,首先补码一位乘法的符号位是参与预算的,附加位初始为0,大体步骤如下:

和原码乘法一样,也需要一个部分积,这里又补充了一个附加位,根据最后两位的情况做对应的操作。最后一次只做操作而不进行位移。写的时候一定要对齐,尽量按照题目给的格式来写,以保证不会出错。

⑦定点数的除法运算
除法运算可以通过累加左移的方式进行,主要分为下面两种方法
a 原码除法计算(不恢复余数)
商符和商值是分开进行的,商符由两个操作数的符号位异或得到,商的数值直接由绝对值做除法得到,除法的方法如下:

除法的计算过程中,符号位单独计算,数值部分除法时,第一步先加上(-y)补,再根据部分余数的情况选择进行哪种操作。重复这个过程,最后一次只上商而不进行补充余数操作。
b 补码除法运算(加减交替法)
加减交替法中,符号位参与运算,根据被除数与除数是否同号来进行不同的操作。具体过程如下:


第一步先看初始状态下除数与被除数的符号,如果相同则进行加法,不同则减,之后开始记录上,同号商1左移一位后减去除数,异号则商0左移一位后加除数,重复这个过程,最后一步末位恒商1。

这一节还有一个很重要的知识点就是C语言中类型的转换,辅导书上说了很多,简答来说就是下面几条:
位数相同的两个类型,数据完全不变,只是改变数据的解释方法。
大字长变量向小字长变量变化时,把高位字长部分直接截断,低位直接赋值。
小子长变量向大字长变量变化时,低位数字保持不变,高位数字扩展为原数字的符号位。
数据的存储和排列部分主要涉及几个小的知识点。
数据的大端存储和小段存储指的是逻辑上的低位字节是否存放在实际的低位字节上。大端方式按从最高有效字节到最低有效字节的顺序存储数据,即最高有效字节存放在前面;小端方式按从最低有效字节到最高有效字节的顺序存储数据,即最低有效字节存放在前面。
排列方面,主要是边界对齐方式的考察。边界对齐是让整个存放更加的整齐,防止在一次取数据的过程中将一个数据被迫拆开,边界不对齐节约了空间但是会让取数据变得很麻烦。就像下面图中展示的那样,如果是一个半字,按照边界不对齐方式,在按字存储时会被拆成两部分,而边界对齐则不会出现这种现象,但是会因为填充导致一定的空间浪费。

2.3 浮点数的表示与运算
浮点数表示不同于定点数的表示,由于小数点是浮动变化的,所以在计算机内的表达也相应的变麻烦了。让小数点根据需要进行浮动,扩大了数的表示范围同时保持了数的有效精度。
浮点数在计算机内的存储方式如下:

阶符与阶码的位数共同反应浮点数的表示范围及小数点的实际位置,数符代表浮点数的符号,尾数的位数表示浮点数的精度。
精度和表示范围是互相限制的,表示范围大则精度就小,精度大表示范围就小。
为了提高运算的精度,就要充分利用尾数的有效数位,即让尾数的最高位必须是一个有效值,让数变得规格化的方法称为规格化操作,规格化的过程本质上就是调整位数的一个过程,即通过调整尾数和阶码的大小来让尾数的最高位上是一个有效值。
规格化有两种:


原码规格化后小数点后面第一位一定是1,补码规格化数位数最高位一定与符号位相反。
当基数为4时原码规格化形式的位数最高两位不全是0,基数为8时原码规格化形式的位数最高三位不全为0。
对于模四补码,当浮点数为正数时,数值位前3位不为全0时是规格化数;当浮点数为负数时,数值位前 3 位不为全1时是规格化数。
浮点数的存储有一个公共的准则,即IEEE754标准,根据此标准,常用的浮点数在计算机内的存储必须满足下面的格式:


该标准规定浮点数是尾数采用隐藏位策略的原码表示,且阶码用移码表示的浮点数。
数符对应这个浮点数的正负,将符号位放在最前面,后面的尾数数值部分就不再考虑符号。
阶码部分用移码来表示,这里的移码的偏置值选的是127,即化简原浮点数后得到的阶码的值要加上127得到的才是IEEE754标准里面的阶码的值,对于长浮点数偏置值是1023。
偏置值有所保留的原因是需要留一些特殊值来表示一些特殊值,当阶码和尾数全为0时表示真值0,阶码全为零而尾数不全为零表示非规格化数,阶码全为1尾数全为零表示无穷大,根据尾数的符号还可以再区分是正无穷还是负无穷。
尾数数值部分采用的是隐藏位的原码,规格化的二进制浮点数,尾数的最高位必然是1,所以在处理时,为了能多表示一位,将这个1隐藏,尾数实际上是24位,但这里只有23位,剩下的最高位1是隐藏的,必要时补上即可。这个地方关于隐藏1的概念比较混乱,所以只要记好让最高位变成1即可,可以结合例子来理解。
个人理解这里的标准化和前面浮点数的标准化实际上是有点差别的,前面提到的原码标准化是让小数点后第一位变成1,这里的标准化不难看出是把第一位变成了1,相当于在标准化的基础上又进行了调整,把第一位的1也给调走了,而相应的阶码的值也会发生变化,所以才有了例子中的表示方法


浮点数只考察加减,相较于定点数,浮点数的加减要简单得多。浮点数的加减运算一律采用补码,运算过程分为下面几步:
①对阶
即让两个操作数的小数点位置对齐,表现为让两个数的阶码相等,对阶的过程中要让小阶向大阶看齐,主要是因为尾数右移可能会导致引丢弃有效位而引起的误差。
②尾数求和
采用双符号位进行补码运算,减法也要用补码进行运算。
③规格化
相加后如果不是规格化则需要进行左归或者右归。当符号位为10或01时需要进行右归,让尾数右移一位阶码加一。当尾数出现为00.0或11.1时需要进行左归(这里采用的是双符号位,相当于前面判断双符号位是否规格化的方法),让尾数左移一位阶码减一,如果还不是规格化就继续左归。
④舍入
对阶或右归过程中可能出现因为舍弃最低位而导致的数据丢失,会一定程度上影响精度。可以采用0舍1入法或者恒置1法
⑤溢出判断
浮点数中尾数的计算结果出现符号位01或10并不表示溢出,需要将数据右归之后再根据阶码来判断是否溢出。
*浮点数运算一定要和IEEE754标准区分开,后者是一种存储标准,在存储时必须满足这个标准,而计算不一定要按照这个标准,如果是按照IEEE754标准进行计算,可以先破坏这个标准的存储,在利用浮点数运算的规则进行计算,最后恢复这个标准,详情见下面例题 *

典型题

这种题更像是知道了就是知道,不知道就只能蒙的题目。CRC通常用于计算机网络的数据链路层,适合对大量数据的数据校验。

很典型的数值计算题,首先题目是32位机,所以需要32位,x为正数,所以在计算机内存储的形式为0000…0111 1111 即十六进制的00000007FH,y为负数,其在计算机用补码形式存在,所以为1111…1111 0111 对应十六进制为FFF7H,z为两者相加的和,直接采取补码相加的方法,这里隐含一个将short类型补位的过程,短变长的补码补充的是符号位,所以全补1,相加结果即00000076H,结果为D。

这种题其实是表面上考察计算,实际上考察8位二进制的表示范围。如果暴力去计算,十分麻烦。正确的做法是将四个整数转化为十进制,8位二进制表示的范围只能是-128~127,而只有B的乘法结果为1568,超过了表示范围,所以B为正确答案。这种问哪个会溢出的题目,直接计算不是可取的方法,最优选择是找表示范围。

一个record对象实际上是占据7B,但是由于采用的是边界对齐存储,所以一个record占据8B。这多出来的1B用于补充char所空出来的1B,所以c的地址为0xC00E,a存放的数据位273,对应十六进制为 0x00000011,而采用小段方式,需要将低数据位放在前面,所以实际存储为0x11000000,故D正确。

题目隐含有一个坑,符号实际上也是占一位的,扣去符号位还剩下n-1位,所以正确答案为D

模 4 补码具有模 2 补码的全部优点且更易检查加减运算中的溢出问题, A 错误。需要注意的是,存储模 4 补码仅需一个符号位,因为任何一个正确的数值,模 4 补码的两个符号位总是相同的,B 正确。只在把两个模4 补码的数送往 ALU 完成加减运算时,才把每个数的符号位的值同时送到 ALU 的双符号位中, 即只在 ALU 中采用双符号位, C、 D 错误。

这道题容易选成B或者C,这是因为BC都是运算出的结果,但不完全,B缺少了右归的步骤,C缺少了检验是否溢出的过程,C是已经规范化的结果,不难看出其阶码是溢出的,所以整个计算结果也是溢出的,只能选D

这道题主要考察的是数据之间的转换。float转换为int会导致小数部分丢失,int转换为float由于位数有差别,所以也有数据丢失。但是Ⅰ 巧妙在只有10位,所以在转换时,没有丢失数据,只丢失了0,对整体没有影响。double的精度和范围都比 float 大,float转换为double 不会有损失,III 正确。Ⅳ在计算时,会由于对阶导致数据丢失,所以最后的结果也发生了变化。故正确答案为B。

这是一道很好的计算例题。
首先两个数都为float类型,需要采用IEEE754标准在计算机内存放。
将X转换为二进制位-(1000100)=-1.0001x2^6,由正负可以看出符号位为1,尾数为1.0001故编码后的小数部分为000 1000 0000 0000 0000 0000,阶码部分为127+6=133=(10000101)所以合并后X对应的二进制为 1 1000 0101 000 1000 0000 0000 0000 0000 即C2880000
转换Y也是同样的道理,区别在于y要处理小数的部分,注意好小数点即可,转换后为C1040000。
剩下两问就是做加减法,这里需要注意,IEEE754标准描述的是浮点数在计算机内的存储格式,实际计算时我们并不一定要在这个格式下进行计算,而是根据浮点数加减的五个步骤来进行计算,所以计算过程没有必要一直保持着IEEE754标准的格式,只需要让计算后的结果再调整为IEEE754标准即可。转换过程一定不要忘了把省略的1补上。计算过程如下:
