【Python 百练成钢】高精度加法、阶乘计算、矩阵幂运算、矩阵面积交

前言

本次分享几道有关于运算方面的算法题,有高精度加法、阶乘运算、矩阵的运算
题情概览：
高精度加法（是进行阶乘计算的前提,模拟的就是我们小学学习的竖式加法运算过程）
阶乘计算（阶乘计算模拟的是竖式乘法）
矩阵的幂运算（模拟矩阵的计算过程、还会分享一下普通矩阵如何转置）
矩阵面积交（探索矩阵顶点之间的关系）

高精度加法

---

问题描述

输入两个整数a和b，输出这两个整数的和。a和b都不超过100位。
算法描述
　　由于a和b都比较大，所以不能直接使用语言中的标准数据类型来存储。对于这种问题，一般使用数组来处理。
　　定义一个数组A，A[0]用于存储a的个位，A[1]用于存储a的十位，依此类推。同样可以用一个数组B来存储b。
　　计算c = a + b的时候，首先将A[0]与B[0]相加，如果有进位产生，则把进位（即和的十位数）存入r，把和的个位数存入C[0]，即C[0]等于(A[0]+B[0])%10。然后计算A[1]与B[1]相加，这时还应将低位进上来的值r也加起来，即C[1]应该是A[1]、B[1]和r三个数的和．如果又有进位产生，则仍可将新的进位存入到r中，和的个位存到C[1]中。依此类推，即可求出C的所有位。
　　最后将C输出即可。
输入格式
　　输入包括两行，第一行为一个非负整数a，第二行为一个非负整数b。两个整数都不超过100位，两数的最高位都不是0。
输出格式
　　输出一行，表示a + b的值。
样例输入
20100122201001221234567890
2010012220100122
样例输出
20100122203011233454668012

问题分析

使用一个临时变量,记录之前相加需要进位的数,也就是说在相加的时候,始终有三个变量在相加,相加之后将存储结果的临时变量的个位取出来,放进结果列表中,然后整除以10,用于下一位置的计算。将数组进行了颠倒是为了便于计算,当较短的数组超出的时候就不必再使用短数组进行运算了。

代码实现

老规矩先上运行结果：

ans=[]
m=[int(x) for x in list(input()[::-1])]
n=[int(x) for x in list(input()[::-1])]

# print(n,m)
temp=0
i=0
minlen=min(len(n),len(m))
maxlen=max(len(n),len(m))
if len(n)>len(m):
    m,n=n,m

while i<maxlen:
    if i<minlen:
        temp=n[i]+m[i]+temp
    else:
        temp=0+m[i]+temp
    ans.append(temp%10)
    temp//=10
    i+=1

print("".join(map(str,ans[::-1])))

阶乘计算

---

问题描述

输入一个正整数n，输出n!的值。
　　其中n!=123*…*n。
算法描述
　　n!可能很大，而计算机能表示的整数范围有限，需要使用高精度计算的方法。使用一个数组A来表示一个大整数a，A[0]表示a的个位，A[1]表示a的十位，依次类推。
　　将a乘以一个整数k变为将数组A的每一个元素都乘以k，请注意处理相应的进位。
　　首先将a设为1，然后乘2，乘3，当乘到n时，即得到了n!的值。
输入格式
　　输入包含一个正整数n，n<=1000。
输出格式
　　输出n!的准确值。
样例输入
10
样例输出
3628800

问题分析

模拟小学学过的乘法计算,只不过小学学的是先乘完后相加,我做的是边乘边相加。

竖式中上面的一行,乘以下面的一个数后得到一行,对下面得到的n行以高精度加法的思想进行相加,每次相加取到的个位就是结果中相应位置的数。为了便于计算我们一列表下标为0的位置作为个位。

代码实现

老规矩先上运行结果：

# 对列表进行运算,低位放在左边
def sumlist(ls1,ls2):
    ans=[]
    # 长的放在后面
    if len(ls1)>len(ls2):
        ls1,ls2=ls2,ls1
    i=0
    temp=0
    while i<len(ls2) or temp!=0:
        if i<len(ls1):
            temp=ls1[i]+ls2[i]+temp
        else:
            temp=ls2[i]+temp
        ans.append(temp%10)
        temp//=10
        i+=1
    
    return ans 



n=int(input())
ans=[0]*3000
ans[0]=1
for i in range(2,n+1):
    j=0
    temp=0
    while j<len(ans) or temp!=0:
        temp=ans[j]*i+temp
        ans[j]=temp%10
        temp//=10
        j+=1

# print(ans)
print(int("".join(map(str,ans[::-1]))))

矩阵幂运算

---

问题描述

给定一个N阶矩阵A，输出A的M次幂（M是非负整数）
　　例如：
　　A = 1 2
　　 3 4
　　A的2次幂
　　7 10
　　15 22
输入格式
　　第一行是一个正整数N、M（1<=N<=30, 0<=M<=5），表示矩阵A的阶数和要求的幂数
　　接下来N行，每行N个绝对值不超过10的非负整数，描述矩阵A的值
输出格式
　　输出共N行，每行N个整数，表示A的M次幂所对应的矩阵。相邻的数之间用一个空格隔开
样例输入
2 2
1 2
3 4
样例输出
7 10
15 22

问题分析

矩阵的运算规则是:一行元素分别乘一列元素的和相加结作为结果矩阵的一位数
例如：A矩阵、B矩阵（能够相乘的前提条件是前面矩阵的列数等于后面矩阵的行数）
ans[_ij]=A的第i行*B的第j列
矩阵的零次幂是对角矩阵
注意：（矩阵进行赋值的时候,需要注意深浅拷贝的问题）

代码实现

老规矩先上运行结果：

# n,m=map(int,input().split())
# mk=[list(map(int,input().split())) for i in range(n)]
# mk1=mk.copy()

# ans=[]
# for i in range(n):
#     ans.append([0 for x in range(n)])

# # 矩阵的零次幂是对角矩阵
# if m==0:
#     for i in range(n):
#         ans[i][i]=1

# #矩阵的非零次幂
# else:
#     for _ in range(m-1):# m次幂
#         ans=[[0 for i in range(n)] for j in range(n)]
#         for j in range(n):# 行
#             for k in range(n):# 列
#                 for t in range(n): # 行*列
#                     ans[j][k]+=mk1[j][t]*mk[t][k]
               
#         mk1=ans.copy()


# for i in ans:
#     print(*i)



import copy
n,m=map(int,input().split())
mk=[list(map(int,input().split())) for i in range(n)]
mk1=mk.copy()

ans=[]
for i in range(n):
    ans.append([0 for x in range(n)])

# 矩阵的零次幂是对角矩阵
if m==0:
    for i in range(n):
        ans[i][i]=1

#矩阵的非零次幂
else:
    temp=0
    for _ in range(m-1):# m次幂
        for j in range(n):# 行
            for k in range(n):# 列
                temp=0
                for t in range(n): # 行*列
                    temp+=mk1[j][t]*mk[t][k]
                ans[j][k]=temp
        # 矩阵之间的赋值需要使用深拷贝,否则会导致数据错乱
        mk1=copy.deepcopy(ans)


for i in ans:
    print(*i)

矩阵转置

矩阵转置的概念就是将矩阵中下标为i，j的元素与矩阵中下标为j，i的元素进行对换
刚开始想到的就是将矩阵进行遍历,兑换，但是比较复杂。本次分享两个简便的方法

①zip函数

大家都知道zip函数可以将可迭代对象进行打包,所以进行矩阵转置的时候可以使用zip函数，将列表
进行打包,打包之后再进行转换为列表即可

②列表推导式

列表推导式是一个非常好用的东西,可以使用列表推导式进行一个转置矩阵的生成。
新生成的矩阵就是转置后的矩阵

矩阵面积交

---

问题描述

平面上有两个矩形，它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形，我们给出它的一对相对顶点的坐标，请你编程算出两个矩形的交的面积。
输入格式
　　输入仅包含两行，每行描述一个矩形。
　　在每行中，给出矩形的一对相对顶点的坐标，每个点的坐标都用两个绝对值不超过10^7的实数表示。
输出格式
　　输出仅包含一个实数，为交的面积，保留到小数后两位。
样例输入
1 1 3 3
2 2 4 4
样例输出
1.00

问题分析

对于矩形他给出的点是相对顶点
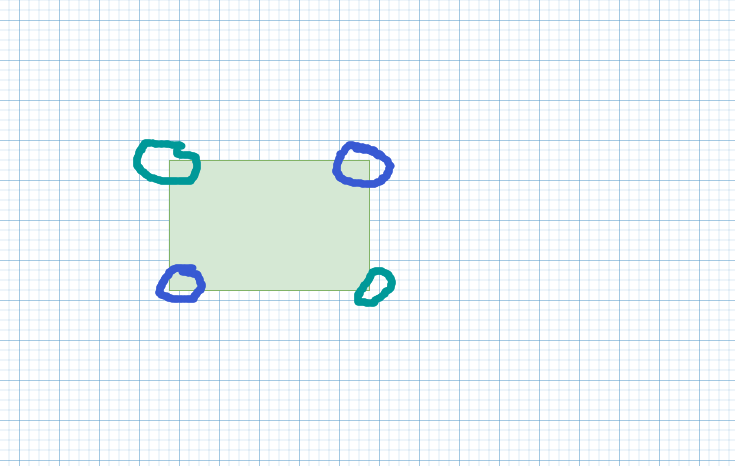
相交的矩形必定位于两个矩形中间,所以相交矩形的相对较小顶点应x坐标该是两矩形最小的x坐标中较大的那一个
相对较大的x顶点应该是两个矩形最大的x中较小的一个。需要考虑两矩形没有相交面积的情况。

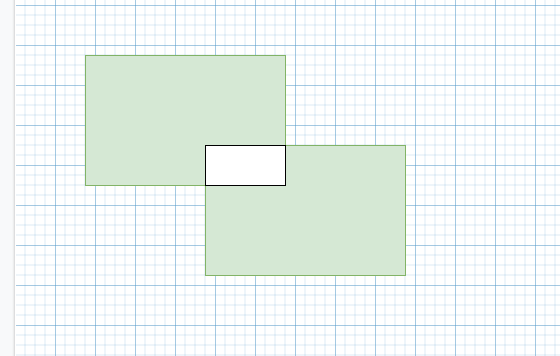
给出的顶点是相对的,矩形的相对顶点围成的矩阵面积是相同的,可以通过转换将绿色顶点围成的矩阵转换为由蓝色顶点围成的矩阵,方法就是将矩阵的最大值x与最大值y挑选出来。

我们倾向于得到白色矩形的面积,我们的处理方式是,在两个绿色矩形的左边找一个较大的x1，在右边找一个较小的x2，同理找y,如果x1>x2证明没有交集,y也是。

代码实现

老规矩先上运行结果：

# 矩形1的两个顶点
r1=list(map(float,input().split()))
# 矩形2的两个顶点
r2=list(map(float,input().split()))


# 如果有相交面积,那么x1
x1=max(min(r1[0],r1[2]),min(r2[0],r2[2]))
x2=min(max(r1[0],r1[2]),max(r2[0],r2[2]))
y1=max(min(r1[1],r1[3]),min(r2[1],r2[3]))
y2=min(max(r1[1],r1[3]),max(r2[1],r2[3]))
if x1<x2 and y1<y2:
    print("{:.2f}".format((x2-x1)*(y2-y1)))
else:
    print("{:.2f}".format(0.00))

---