【2021.12.22】数学基础

---

实验一（求最大公因数）

1.1 实验要求

编写程序实现计算任意两个整数a 与b的最大公因数d=(a,b)，要
求即使a与b中的一个等于零，程序也应该正常运行。用你编写的程序求解GCD（16534528044,8332745927）以及（你的学号，你的学号+你的班级号+你的座位号）

1.2 设计思路

使用欧几里得算法，如果a或b为0，则直接返回最大公因数0，因为测试数据数较大，所以a b都使用了长整型定义。

1.3 测试数据

自己测

1.4 测试结果

自己测

1.5 调试过程中发现的问题与解决办法

发现的问题:在输入第一组测试数据后,再输入第二组数据,发现输出最大公因数为自己的学号（不可能为正确答案）。
解决办法:通过调试发现因为while循环的位置不对，abr的值未被初始化,将while放在最上面即可。

1.6 源程序

#include
using namespace std;
int main() {
	while (1) {
		long long int a = 0;
		long long int b = 0;
		long long int r = -1;
		cout << "请输入整数a和b" << endl;
		cin >> a;
		cin >> b;
		if (a < 0) { a = -a; }
		if (b < 0) { b = -b; }//将负数转化为正数
		if (a == b) {
			cout << "最大公因数为" << a << endl;;
		}
		else if (a == 0 || b == 0)
		{
			cout << "最大公因数为0" << endl;;
		}
		else {
			while (r != 0)
			{
				r = a % b;
				a = b;
				b = r;//欧几里得算法
			}
			cout << "最大公因数为" << a << endl;;

		}
	}
	return 0;
}

实验二（因式分解）

2.1 实验要求

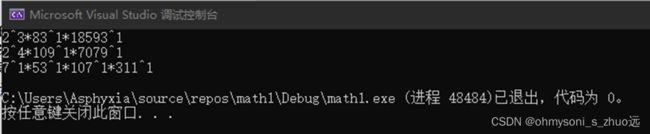
编写程序求12345678与12345678+你的学号最后三位整数之间任选3个整数的因式分解，并用比较优美的格式打印出来，格式参考：
2^5*36

2.2 设计思路

定义一个数字结构体numb，包含底数和指数。
先生成12345678~12345850之间的一位数，将小于其开根后的数的所有素数存入一个数组中，然后让被测试的数反复的去模这些素数，如果能除尽则说明该素数是被测试数的因子，将其存入numb类型的向量中，如果底数未存入过，则存入，如果底数在向量中已出现过，则指数加一。同时被测试数也应相应变成商。如此反复，直至模完素数数组。最后根据底数对结果进行排序，得到结果。

2.3 测试数据

12345752 12345776 12345767

2.4 测试结果

2.5 调试中发现的问题与解决办法

发现的问题后面行的结果中会出现前面行的结果,问题在每次循环忘记重置向量。
解决办法:每次循环前调用vector的clear（）函数。
发现的问题:每次num的值与分解的数的乘积不一致。
解决办法:如果某素数是被测试数的因子,素数在存入向量的同时,被测试数也应该化为商的大小。

2.6 源程序

#include
#include
using namespace std;
struct numb {
	long long int  num;//底数
	int index;//指数
};
bool isPrime(long long int n) {
	for (long long int i = 2; i <= sqrt(n); i++) {
		if ((n % i) == 0) {
			return 0;
		}
	}
	return 1;
}
int main() {
	srand(time(NULL));
	vector<long long int>prime;
	vector<numb>a;
	for (int i = 0; i < 3; i++) {
		prime.clear();
		a.clear();
		long long int  num = 12345678+rand()%172;
		if (isPrime(num) == 1) {
			cout << num << endl;
			continue;
		}
		double temp = sqrt(num);
		temp = (int)temp;
		for (int j = 2; j < temp; j++) {//生成素数数组
			int ans = isPrime(j);
			if (ans == 1) {
				prime.push_back(j);
			}
			else {
				continue;
			}
		}
		for (int i = 0; i < prime.size(); i++) {
			int x = num % prime[i];
			if (x==0) {
				vector<numb>::iterator it;
				for (it = a.begin(); it != a.end(); it++) {
					if (it->num == prime[i]) {
						it->index++;
						break;
					}
				}
			    if(it==a.end()){
					a.push_back({ prime[i],1 });
					
				}
				num = num / prime[i];
				i = -1;
				continue;
			}
			else { continue; }
		}
		for (int i = 0; i < a.size() - 1; i++){
			for (int j = 1; j < a.size(); j++) {
				if (a[j - 1].num > a[j].num) {
					numb temp;
					temp.num = a[j - 1].num;
					temp.index = a[j - 1].index;
					a[j - 1].num = a[j].num;
					a[j - 1].index = a[j].index;
					a[j].num = temp.num;
					a[j].index = temp.index;
				}
			}
		}
		for (int m = 0; m < a.size(); m++) {
			if (m != 0) { cout << "*"; }
			cout << a[m].num << "^" << a[m].index;
		 }
		if (num != 1) {
			cout << "*" << num<<"^1";
		}
		cout << endl;
	}
	return 0;
}

实验三（求逆元）

3.1实验要求

编写程序求解a在模b下的逆元a^(-1),并具体求解当（a,b）为
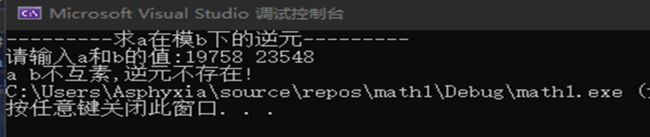
（i）（19789,23548）
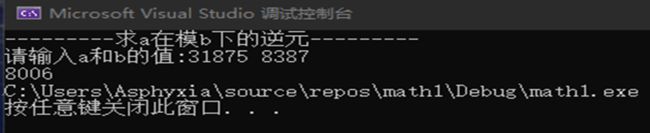
（ii）（31875,8387）时的解

3.2设计思路

利用for循环测试从1到b的每一个数，如果该数与a相乘模b得到1，那么该数为a在模b下的逆元。循环结束都未得到逆元，则说明a和b不互素，没有逆元存在。

3.3 测试数据

（19758,23548） （31875,8387）

3.4 测试结果

3.5调试过程中发现的问题与解决办法

发现的问题:没考虑到a,b不互素时不存在逆元的情况。
解决办法:在找逆元的循环结束后提示不存在逆元,返回-1不输出直接结束程序。

3.6 源程序

#include
using namespace std;
int getInverse(int M, int m) {
	int i = 0;
	for (i = 1; i < m; i++) {
		if ((M * i) % m == 1) {
			return i;
		}
	}
	cout << "a b不互素,逆元不存在!";
	return -1;
}
int main() {
	cout << "---------求a在模b下的逆元---------" << endl;
	cout << "请输入a和b的值:";
	int a, b;
	cin >> a;
	cin >> b;
	int inverser_element = getInverse(a, b);
	if (inverser_element == -1) { return 0; }
	else {
		cout << inverser_element;
	}
	return 0;
}

还是用扩展的欧几里得比较好 上面这个复杂度太高了

void exgcd(ll a, ll b, ll& d, ll& x, ll& y)
{
	if (b == 0)
	{
		d = a; x = 1; y = 0; return;
	}
	exgcd(b, a % b, d, y, x);
	y -= (a / b) * x;
}
ll rev(ll t, ll m)
{  
	ll d, x, y;
	exgcd(t, m, d, x, y);
	return (x % m + m) % m;
}

int main(){
ll e;
ll fain;
	ll d = rev(e, fain);//d就是emodfain的逆元
return 0；

实验五（中国剩余定理）

5.1 实验要求

编写程序利用中国剩余定理求解
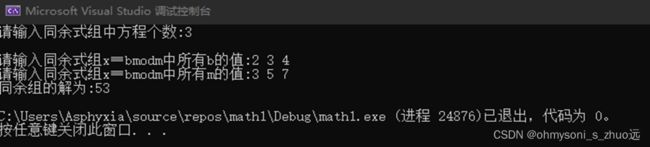
1） 今有物不知其数 三三数之剩二 五五数之剩三 七七数之剩四 问物几何？
2） 某个数模10余4，模13余6，模7余4，模11余2，求满足这个条件的最小正整数。

5.2 设计思路

定义数组b[],m[]，分别用来存储同余式x≡bmodm中的bi、mi。
定义数组M[],Mi为所以m的积除以mi。定义_M[],_M[i]为M[i]模m[i]的逆元。
然后可以轻松得到x=b1*_M1M1+b2_M2M2+…+bk_Mk*Mk.

5.3 测试数据

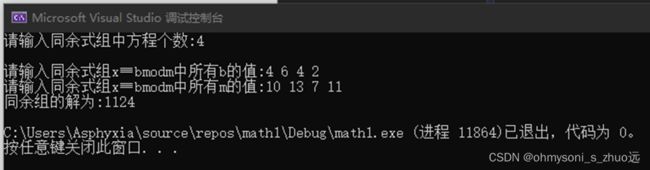
3 2 3 4 3 5 7
4 4 6 4 2 10 13 7 11

5.4 测试结果

5.5 调试过程中发现的问题与解决办法

发现的问题:无

5.6 源程序

#include
using namespace std;
int getInverse(int M, int m) {
	int i = 0;
	for (i = 1; i < m; i++) {
		if ((M * i) % m == 1) {
			return i;
		}	
}
cout << "a b不互素!";
	return -1;

}
#define SIZE 100
int b[SIZE];
int m[SIZE];
int M[SIZE];
int _M[SIZE];//逆元
int main() {
	int cnt;
	cout << "请输入同余式组中方程个数:";
	cin >> cnt;
	cout << endl;
	cout << "请输入同余式组x≡bmodm中所有b的值:";
	for (int i = 0; i < cnt; i++) {
		cin >> b[i];
	}
	cout << "请输入同余式组x≡bmodm中所有m的值:";
	for (int i = 0; i < cnt; i++) {
		cin >> m[i];
	}
	int product = 1;
	for (int i = 0; i < cnt; i++) {//计算所有m相乘得到的积
		product = product * m[i];
	}
	for (int i = 0; i < cnt; i++) { //计算各Mi
		M[i] = product / m[i];
	}
	for (int i = 0; i < cnt; i++) {//计算Mi'
		_M[i] = getInverse(M[i], m[i]);
	}
	int x=0;
	for (int i = 0; i < cnt; i++) {
		x += (b[i] * _M[i] * M[i]);
	}
	x = x % product;
	cout << "同余组的解为:" << x << endl;
	return 0;
}

实验六:(RSA)

6.1 实验要求

你向外发送的信息如下
5272281348, 21089283929,3117723025, 26844144908, 22890519533, 26945939925,
27395704341, 2253724391, 1481682985, 2163791130, 13583590307, 5838404872, 12165330281, 501772358, 7536755222
该信息使用RSA进行加密,参数如下,p=187963,q=163841,n=pq=30796045883,公钥为e=48611.
试着解密该信息（注意,最后得到的数字需要整体平移，才能得到有意义的明文）（私钥后四个数字是5691）

6.2 设计思路

6.3 测试数据

5272281348, 21089283929,3117723025, 26844144908, 22890519533, 26945939925,
27395704341, 2253724391, 1481682985, 2163791130, 13583590307, 5838404872, 12165330281, 501772358, 7536755222