win10+Python3.7.3+OpenCV3.4.1入门学习(十二 图像轮廓)————12.5 轮廓拟合
Python版本是Python3.7.3,OpenCV版本OpenCV3.4.1,开发环境为PyCharm
文章目录
-
- 12.5 轮廓拟合
-
- 12.5.1 矩形包围框
- 12.5.2 最小包围矩形框
- 12.5.3 最小包围圆形
- 12.5.4 最优拟合椭圆
- 12.5.5 最优拟合直线
- 12.4.6 最小外包三角形
- 12.4.7 逼近多边形
12.5 轮廓拟合
在计算轮廓时,可能并不需要实际的轮廓,而仅需要一个接近于轮廓的近似多边形。OpenCV提供了多种计算轮廓近似多边形的方法。
本节的部分程序使用了绘图函数,这些函数在第19章中有详细的介绍,这里不再赘述。
12.5.1 矩形包围框
函数cv2.boundingRect()能够绘制轮廓的矩形边界。该函数的语法格式为:
retval = cv2.boundingRect( array )
式中:
● 返回值retval表示返回的矩形边界的左上角顶点的坐标值及矩形边界的宽度和高度。
● 参数array是灰度图像或轮廓。
该函数还可以是具有4个返回值的形式:
x, y, w, h = cv2.boundingRect( array )
这里的4个返回值分别表示:
● 矩形边界左上角顶点的x坐标。
● 矩形边界左上角顶点的y坐标。
● 矩形边界的x方向的长度。
● 矩形边界的y方向的长度。
eg1:设计程序,显示函数cv2.boundingRect()不同形式的返回值。
代码如下:
import cv2
#---------------读取并显示原始图像------------------
o = cv2.imread('cc.bmp')
#---------------提取图像轮廓------------------
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
image,contours, hierarchy = cv2.findContours(binary,
cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
#---------------返回顶点及边长------------------
x,y,w,h = cv2.boundingRect(contours[0])
print("顶点及长宽的点形式:")
print("x=",x)
print("y=",y)
print("w=",w)
print("h=",h)
#---------------仅有一个返回值的情况------------------
rect = cv2.boundingRect(contours[0])
print("\n顶点及长宽的元组(tuple)形式:")
print("rect=",rect)
运行上述程序,显示如下结果:
顶点及长宽的点形式:
x= 202
y= 107
w= 157
h= 73
顶点及长宽的元组(tuple)形式:
rect= (202, 107, 157, 73)
eg2:使用函数cv2.drawContours()绘制矩形包围框。
代码如下:
import cv2
import numpy as np
#---------------读取并显示原始图像------------------
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
#---------------提取图像轮廓------------------
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
image,contours, hierarchy = cv2.findContours(binary,
cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
#---------------构造矩形边界------------------
x,y,w,h = cv2.boundingRect(contours[0])
brcnt = np.array([[[x, y]], [[x+w, y]], [[x+w, y+h]], [[x, y+h]]])
cv2.drawContours(o, [brcnt], -1, (255, 255,255), 2)
#---------------显示矩形边界------------------
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()
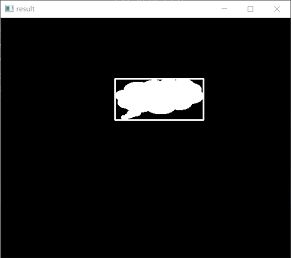
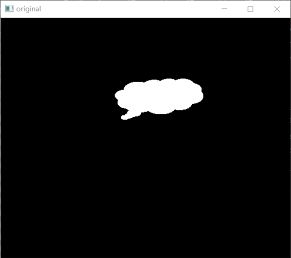
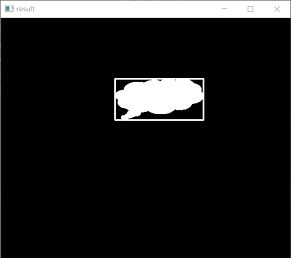
运行上述程序,会显示如下图所示的图像,其中:
● 左图是原始图像o。
● 右图是在原始图像外绘制矩形包围框后的结果。
eg3:使用函数cv2.boundingRect()及cv2.rectangle()绘制矩形包围框。
函数cv2.rectangle()可以用来绘制矩形,有关该函数的详细介绍可以参考第19章。
代码如下:
import cv2
#---------------读取并显示原始图像------------------
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
#---------------提取图像轮廓------------------
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
image,contours, hierarchy = cv2.findContours(binary,
cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
#---------------构造矩形边界------------------
x,y,w,h = cv2.boundingRect(contours[0])
cv2.rectangle(o,(x,y),(x+w,y+h),(255,255,255),2)
#---------------显示矩形边界------------------
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()
运行上述程序,会显示如下图所示的图像,其中:
12.5.2 最小包围矩形框
函数cv2.minAreaRect()能够绘制轮廓的最小包围矩形框,其语法格式为:
retval =cv2.minAreaRect( points )
式中:
● 返回值retval表示返回的矩形特征信息。
该值的结构是(最小外接矩形的中心(x, y), (宽度,高度),旋转角度)。
● 参数points是轮廓。
**需要注意,返回值retval的结构不符合函数cv2.drawContours()的参数结构要求。因此,必须将其转换为符合要求的结构,才能使用。函数cv2.boxPoints()能够将上述返回值retval转换为符合要求的结构。**函数cv2.boxPoints()的语法格式是:
points = cv2.boxPoints( box )
式中:
● 返回值points,是能够用于函数cv2.drawContours()参数的轮廓点。
● 参数box是函数cv2.minAreaRect()返回值的类型的值。
eg4:使用函数cv2.minAreaRect()计算图像的最小包围矩形框。
代码如下:
import cv2
import numpy as np
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
image,contours, hierarchy = cv2.findContours(binary,
cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
rect = cv2.minAreaRect(contours[0])
print("返回值rect:\n",rect)
points = cv2.boxPoints(rect)
print("\n转换后的points:\n",points)
points = np.int0(points) #取整
image=cv2.drawContours(o,[points],0,(255,255,255),2)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()
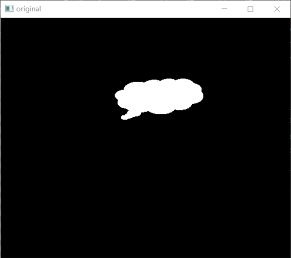
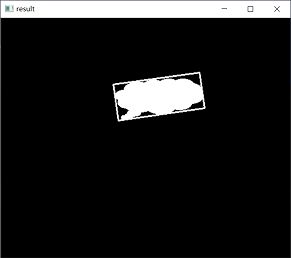
运行上述程序,会显示如下图所示的图像:
● 左图是原始图像o。
● 右图显示了最小包围矩形框。
同时,程序还会输出如下结果:
返回值rect:
((280.3699951171875, 138.58999633789062), (154.99778747558594, 63.78103256225586), -8.130102157592773)
转换后的points:
[[208.16002 181.12 ]
[199.14 117.979996]
[352.57996 96.06 ]
[361.59998 159.2 ]]
从输出结果可以看出:
● 返回值rect表示返回的矩形特征信息。
该值的结构是(最小外接矩形的中心(x, y), (宽度,高度),旋转角度)
● 转换后的points是一些点,是能够用作函数cv2.drawContours()参数的轮廓点。
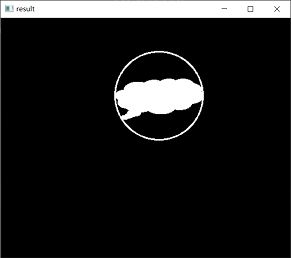
12.5.3 最小包围圆形
函数cv2.minEnclosingCircle()通过迭代算法构造一个对象的面积最小包围圆形。该函数的语法格式为:
center, radius = cv2.minEnclosingCircle( points )
式中:
● 返回值center是最小包围圆形的中心。
● 返回值radius是最小包围圆形的半径。
● 参数points是轮廓。
eg5:使用函数cv2.minEnclosingCircle()构造图像的最小包围圆形。
:代码如下:
import cv2
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
image,contours, hierarchy = cv2.findContours(binary,
cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
(x,y),radius = cv2.minEnclosingCircle(contours[0])
center = (int(x),int(y))
radius = int(radius)
cv2.circle(o,center,radius,(255,255,255),2)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()
本例中调用了函数cv2.circle(),有关该函数的详细说明请参考第19章。
运行上述程序,会显示如下图所示的图像。其中:
● 左图是图像o。
● 右图是含有最小包围圆形的图像。
12.5.4 最优拟合椭圆
在OpenCV中,函数cv2.fitEllipse()可以用来构造最优拟合椭圆。该函数的语法格式是:
retval = cv2.fitEllipse( points )
式中:
● 返回值retval是RotatedRect类型的值。这是因为该函数返回的是拟合椭圆的外接矩形,retval包含外接矩形的质心、宽、高、旋转角度等参数信息,这些信息正好与椭圆的中心点、轴长度、旋转角度等信息吻合。
● 参数points是轮廓。
eg6:使用函数cv2.fitEllipse()构造最优拟合椭圆。
本例需要使用函数cv2.ellipse()根据函数cv2.fitEllipse()的返回值绘制最优拟合椭圆。有关函数cv2.ellipse()的用法,请参考第19章。
代码如下:
import cv2
o = cv2.imread('cc.bmp')
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
image,contours, hierarchy = cv2.findContours(binary,
cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
cv2.imshow("original",o)
ellipse = cv2.fitEllipse(contours[0])
print("ellipse=",ellipse)
cv2.ellipse(o,ellipse,(0,255,0),3)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()
运行上述程序,会显示如下图所示的图像。其中:
● 左图是图像o。
● 右图是包含了最优拟合椭圆的图像。
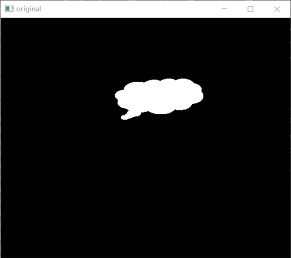
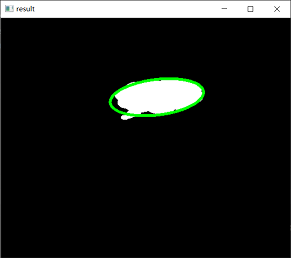
同时,程序还会显示如下的运行结果:
ellipse= ((276.2112731933594, 139.6067352294922), (63.01350021362305, 166.72308349609375), 82.60102844238281)
上述运行结果中:
● (276.2112731933594, 139.6067352294922)是椭圆的中心点。
● (63.01350021362305, 166.72308349609375)是椭圆的轴长度。
● 82.60102844238281是椭圆的旋转角度。
12.5.5 最优拟合直线
在OpenCV中,函数cv2.fitLine()用来构造最优拟合直线,该函数的语法格式为:
式中line为返回值,是返回的最优拟合直线参数。
line = cv2.fitLine( points, distType, param, reps, aeps )
式中的参数如下:
● points:轮廓。
● distType:距离类型。拟合直线时,要使输入点到拟合直线的距离之和最小,其类型如下表所示。
● param:距离参数,与所选的距离类型有关。当此参数被设置为0时,该函数会自动选择最优值。
● reps:用于表示拟合直线所需要的径向精度,通常该值被设定为0.01。
● aeps:用于表示拟合直线所需要的角度精度,通常该值被设定为0.01。

eg7:使用函数cv2.fitLine()构造最优拟合直线。
代码如下:
import cv2
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
image,contours, hierarchy = cv2.findContours(binary,
cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
rows,cols = image.shape[:2]
[vx,vy,x,y] = cv2.fitLine(contours[0], cv2.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx) + y)
righty = int(((cols-x)*vy/vx)+y)
cv2.line(o,(cols-1,righty),(0,lefty),(0,255,0),2)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()
运行上述程序,会显示如下图所示。其中:
● 左图是图像o。
● 右图是包含了最优拟合直线的图像。
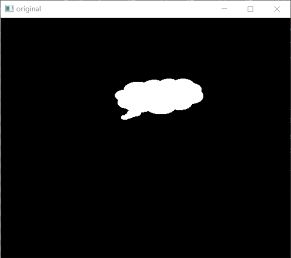
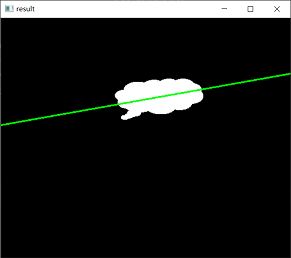
12.4.6 最小外包三角形
在OpenCV中,函数cv2.minEnclosingTriangle()用来构造最小外包三角形。该函数的语法格式为:
retval, triangle = cv2.minEnclosingTriangle( points )
式中有两个返回值:
● retval:最小外包三角形的面积。
● triangle:最小外包三角形的三个顶点集。
式中的参数points是轮廓。
eg8:使用函数cv2.minEnclosingTriangle()构造最小外包三角形。
:代码如下:
import cv2
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
image,contours, hierarchy = cv2.findContours(binary,
cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
area,trgl = cv2.minEnclosingTriangle(contours[0])
print("area=",area)
print("trgl:",trgl)
for i in range(0, 3):
cv2.line(o, tuple(trgl[i][0]),
tuple(trgl[(i + 1) % 3][0]), (255,255,255), 2)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()
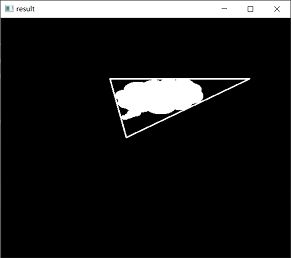
运行上述程序,会显示如下图所示的图像。其中:
● 左图是图像o。
● 右图是包含最小外包三角形的图像。
area= 12904.00390625
trgl: [[[193.25641 107. ]]
[[222.58975 211. ]]
[[441.41025 107. ]]]
从上述结果可以看出:
● 返回值area是最小外包三角形的面积。
● 返回值trgl是最小外包三角形的三个顶点。
12.4.7 逼近多边形
函数cv2.approxPolyDP()用来构造指定精度的逼近多边形曲线。该函数的语法格式为:
approxCurve = cv2.approxPolyDP( curve, epsilon, closed )
式中,返回值approxCurve为逼近多边形的点集。
式中的参数如下:
● curve是轮廓。
● epsilon为精度,原始轮廓的边界点与逼近多边形边界之间的最大距离。
● closed是布尔型值。该值为True时,逼近多边形是封闭的;否则,逼近多边形是不封闭的。
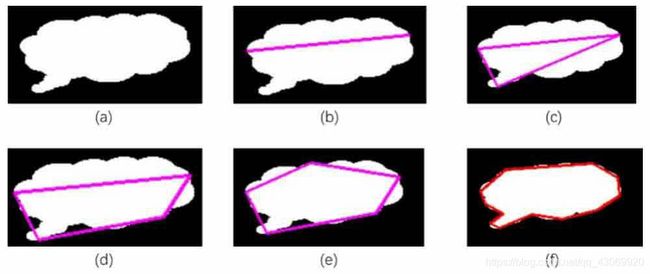
函数cv2.approxPolyDP()采用的是Douglas-Peucker算法(DP算法)。以下图为例,该算法首先从轮廓中找到距离最远的两个点,并将两点相连(见下图的(b)图)。接下来,在轮廓上找到一个离当前直线最远的点,并将该点与原有直线连成一个封闭的多边形,此时得到一个三角形,如下图中的©图所示。
将上述过程不断地迭代,将新找到的距离当前多边形最远的点加入到结果中。当轮廓上所有的点到当前多边形的距离都小于函数cv2.approxPolyDP()的参数epsilon的值时,就停止迭代。最终可以得如下图的(f)图所示的处理结果。
通过上述过程可知,epsilon是逼近多边形的精度信息。通常情况下,将该精度设置为多边形总长度的百分比形式。
eg9:使用函数cv2.approxPolyDP()构造不同精度的逼近多边形。
代码如下:
import cv2
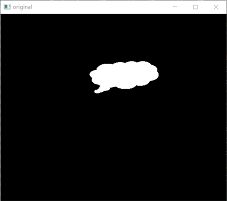
#----------------读取并显示原始图像-------------------------------
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
#----------------获取轮廓-------------------------------
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
image,contours, hierarchy = cv2.findContours(binary,
cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
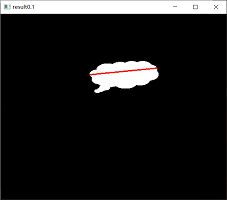
#----------------epsilon=0.1*周长-------------------------------
adp = o.copy()
epsilon = 0.1*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.1",adp)
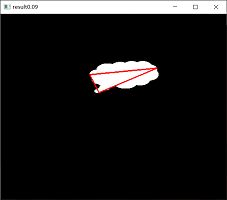
#----------------epsilon=0.09*周长-------------------------------
adp = o.copy()
epsilon = 0.09*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.09",adp)
#----------------epsilon=0.055*周长-------------------------------
adp = o.copy()
epsilon = 0.055*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.055",adp)
#----------------epsilon=0.05*周长-------------------------------
adp = o.copy()
epsilon = 0.05*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.05",adp)
#----------------epsilon=0.02*周长-------------------------------
adp = o.copy()
epsilon = 0.02*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.02",adp)
#----------------等待释放窗口-------------------------------
cv2.waitKey()
cv2.destroyAllWindows()
运行上述程序,会显示如下图所示的图像。其中:
● ( a )图是图像o。
● ( b )图显示了“epsilon=0.1周长”的逼近多边形(实际上,在第1次的查找过程中仅仅找到了一条直线)。
● ( c )图显示了“epsilon=0.09周长”的逼近多边形。
● ( d )图显示了“epsilon=0.055周长”的逼近多边形。
● ( e )图显示了“epsilon=0.05周长”的逼近多边形。
● ( f )图显示了“epsilon=0.02*周长”的逼近多边形。
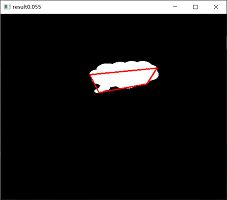
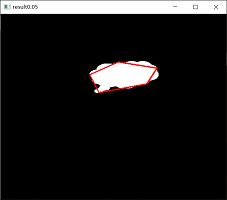

从程序运行结果可以看出,在函数cv2.approxPolyDP()中通过参数epsilon可以控制逼近多边形的精度。
需要注意:本节中使用的图像都是仅有一个轮廓的图像,处理的轮廓都是contours[0]。如果处理的原图像中有多个轮廓,则需要注意控制轮廓的索引,即contours[i]中的i值,使其指向特定的轮廓。