机器学习偏差与方差

一、应用机器学习的建议
（1）模型预测未知数据时发现有较大误差，可考虑采用下面的几种方法：
1、收集更多的训练样本；
2、尝试减少特征的数量；
3、尝试获得更多的特征；
4、尝试增加多项式特征；
5、尝试减少正则化参数λ；
6、尝试增加正则化参数λ。
（2）评估假设函数的方法：将数据分成训练集和测试集，典型的分割方法是按照7：3的比例（随机）。对训练集进行学习得到参数θ，利用测试集计算测试误差，即代价函数J。
（3）从多个模型中选择一个更能适应一般情况的模型，可以使用交叉验证集。把数据分为三个部分，training set训练集、cross validation set交叉验证集cv、test set测试集，典型比例是6：2：2。模型选择的方法是：
1、使用训练集训练出多个模型；
2、用这些模型分别对交叉验证集计算出交叉验证误差；
3、选取交叉验证误差最小的模型；
4、用步骤3选出的模型对测试集计算得出泛化误差。

（4）模型欠拟合时，偏差较大。模型过拟合时，方差较大。判断模型属于哪种问题，可以将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图上分析：

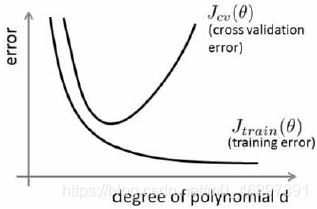
多项式次数低时，训练误差和验证误差都大，两者接近，模型欠拟合；次数高时，训练误差小，验证误差大，后者远大于前者，模型过拟合。
（5）正则化参数λ太大时，模型欠拟合，偏差较大。正则化参数λ太小时，模型过拟合，方差较大。λ值的选择通常是0—10之间的呈现2倍关系的值，如0,0.01,0.02,0.04,0.08,0.16,0.32,…,10。选择λ的方法为：
1、使用训练集训练出多个不同程度正则化的模型；
2、用这些模型分别对交叉验证集计算出交叉验证误差；
3、选择出交叉验证误差最小的模型；
4、运用步骤3选出的模型对测试集计算出泛化误差，同时将训练集和交叉验证集模型的代价函数误差与λ的值绘制在一张图上：

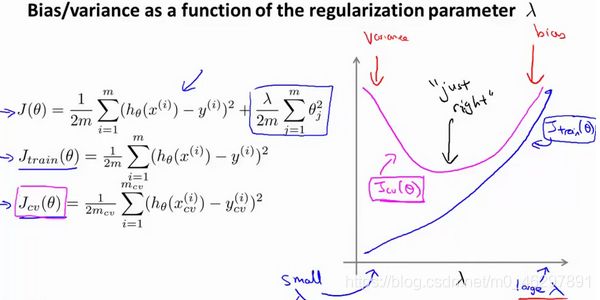
当λ较小时，训练集误差较小而交叉验证集误差较大。随着λ的增加，训练集误差不断增加，而交叉验证集误差则是先减小后增加。
（6）学习曲线可以判断算法是否处于偏差、方差问题，它将训练集误差和交叉验证集误差作为训练集样本数量（m）的函数绘制图表。当训练较少行数据的时候，模型能够非常完美地适应较少的训练数据，但是不能很好地适应交叉验证集数据或测试集数据。

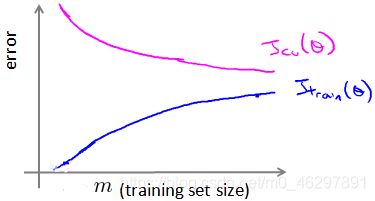
在高偏差即欠拟合的情况下，训练集增加数据不一定有帮助。在高方差即过拟合的情况下，训练集增加数据可能可以提高算法效果。
（7）针对偏差和方差问题的改进策略：
1、获得更多的训练样本——解决高方差；
2、尝试减少特征的数量——解决高方差；
3、尝试获得更多的特征——解决高偏差；
4、尝试增加多项式特征——解决高偏差；
5、尝试减少正则化程度λ——解决高偏差；
6、尝试增加正则化程度λ——解决高方差。
简单神经网络参数较少，容易欠拟合，但计算量小；复杂神经网络参数较多，容易过拟合，可使用正则化来修正。通常选择较大的神经网络并采用正则化处理比采用较小的神经网络效果要好。
（8）构建一个学习算法的推荐方法为：
1、从一个简单的能快速实现的算法开始，实现该算法并用交叉验证集测试这个算法；
2、绘制学习曲线，决定是增加更多数据，或者添加更多特征，还是其他提高算法表现的选择；
3、进行误差分析：人工检查交叉验证集中算法预测错误的样本，看看这些样本是否有某种系统化的趋势。
二、以吴恩达机器学习课程练习材料实现，使用线性回归来研究具有不同偏差-方差属性的模型。背景是基于水库水位的变化来预测大坝的出水量。代码实现来源参考：吴恩达机器学习作业Python实现(五)：偏差和方差。
原始数据集以matlab的数据存储格式.mat保存，数据集共分为三部分：训练集、交叉验证集和测试集，其中x表示水位的变化，y表示大坝的出水量。
原始数据处理代码如下：

from scipy.io import loadmat
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as opt

data = loadmat('bias_va.mat')  #读取matlab格式的数据集
#print(data.keys())
X, y = data['X'], data['y'] #获得训练集数据
Xval, yval = data['Xval'], data['yval'] #获得交叉验证集数据
Xtest, ytest = data['Xtest'], data['ytest'] #获得测试集数据
X = np.insert(X, 0, 1, axis=1)  #各特征集前面添加一列1，以便计算截距项
Xval = np.insert(Xval, 0, 1, axis=1)
Xtest = np.insert(Xtest, 0, 1, axis=1)
#print(X.shape,y.shape)
#print(Xval.shape,yval.shape)
#print(Xtest.shape,ytest.shape)

相关函数实现代码如下：

def plotData(): #绘制训练集数据
    plt.figure(figsize=(8, 5))  #设置图的大小
    plt.scatter(X[:, 1:], y, c='r', marker='x') #绘制数据点
    plt.xlabel('Change in water level (x)') #设置坐标轴名称
    plt.ylabel('Water flowing out of the dam (y)')
    plt.grid()  #显示网格线

#正则化的线性回归代价函数
def costReg(theta, X, y, lm):
    cost = ((X @ theta - y.flatten())**2).sum() #原本代价值
    regterm = lm * (theta[1:] @ theta[1:])  #正则项
    return (cost + regterm) / (2 * len(X))

#正则化梯度
def gradientReg(theta, X, y, lm):
    grad = (X @ theta - y.flatten()) @ X    #原本梯度
    regterm = lm * theta    #正则化项
    regterm[0] = 0  #偏置项不正则化
    return (grad + regterm) / len(X)

#训练线性回归模型
def trainLinearReg(X, y, lm):
    theta = np.zeros(X.shape[1])    #初始化参数
    res = opt.minimize(fun=costReg, x0=theta, args=(X, y, lm), method='BFGS', jac=gradientReg)  #使用minimize，fun是优化的目标函数，x0定义初值，args元组是传递给优化函数的参数，method是求解的算法，jac提供梯度函数
    return res.x #返回最终参数

#绘制学习曲线
def plot_learning_curve(X, y, Xval, yval, lm):
    xx = range(1, len(X) + 1)
    train_cost, cv_cost = [], []    #存储不同样本量的训练误差和交叉验证误差
    for i in xx:    #从1开始逐渐增加样本量，训练出不同的参数向量θ，计算训练代价和交叉验证代价
        res = trainLinearReg(X[:i], y[:i], lm)
        training_cost_i = costReg(res, X[:i], y[:i], lm)
        cv_cost_i = costReg(res, Xval, yval, lm)
        train_cost.append(training_cost_i)
        cv_cost.append(cv_cost_i)
    plt.figure(figsize=(8, 5))  #设置图的大小
    plt.plot(xx, train_cost, label='training cost') #绘制训练误差
    plt.plot(xx, cv_cost, label='cv cost')  #绘制交叉验证误差
    plt.legend()    #添加图例
    plt.xlabel('Number of training examples')   #设置坐标轴名称
    plt.ylabel('Error')
    plt.title('Learning curve for linear regression')   #设置标题
    plt.grid()  #显示网格线
    plt.show()

#添加多项式特征
def genPolyFeatures(X, power):
    Xpoly = X.copy()    #复制原特征进行拓展
    for i in range(2, power + 1):
        Xpoly = np.insert(Xpoly, Xpoly.shape[1], np.power(Xpoly[:, 1], i), axis=1)  #从二次方开始插入，每次在最后一列插入第二列（一次项）的i次方
    return Xpoly

#获取训练集的均值和标准差
def get_means_std(X):
    means = np.mean(X, axis=0)  #获得每一列特征的均值
    stds = np.std(X, axis=0, ddof=1)    #获得每一列特征的标准差，ddof=1表示样本标准差
    return means, stds

#特征标准化
def featureNormalize(X, means, stds):
    X_norm = X.copy()
    X_norm[:, 1:] = X_norm[:, 1:] - means[1:]   #用训练集的均值和样本标准差对偏置项以外的特征进行标准化
    X_norm[:, 1:] = X_norm[:, 1:] / stds[1:]
    return X_norm

模型优化过程相关代码如下：

#直接对原始数据进行线性回归
fit_theta = trainLinearReg(X, y, 0)  #训练模型
plotData()  #绘制训练集数据
plt.plot(X[:, 1], X @ fit_theta)    #绘制拟合直线
plt.show()
#plot_learning_curve(X,y,Xval,yval,0)

#添加多项式特征后进行线性回归
power = 6   #扩展到X的6次方
train_means, train_stds = get_means_std(genPolyFeatures(X, power))  #获取添加多项式特征后的训练集均值和标准差
X_norm = featureNormalize(genPolyFeatures(X, power), train_means, train_stds)   #各特征集添加多项式特征后标准化
Xval_norm = featureNormalize(genPolyFeatures(Xval, power), train_means, train_stds)
Xtest_norm = featureNormalize(genPolyFeatures(Xtest, power), train_means, train_stds)
#绘制拟合曲线
def plot_fit(means, stds, lm):
    theta = trainLinearReg(X_norm, y, lm)   #训练参数
    x = np.linspace(-75, 55, 50)    #生成x轴
    xmat = x.reshape(-1, 1) #数据更改为只有一列的形式
    xmat = np.insert(xmat, 0, 1, axis=1)    #前面插入偏置项
    Xmat = genPolyFeatures(xmat, power) #添加多项式特征
    Xmat_norm = featureNormalize(Xmat, means, stds) #标准化
    plotData()  #绘制训练集数据
    plt.plot(x, Xmat_norm @ theta, 'b--')   #绘制拟合曲线，'b--'生成蓝色虚线
    plt.show()
plot_fit(train_means,train_stds,1)
plot_learning_curve(X_norm,y,Xval_norm,yval,1)  

#通过交叉验证选择正则化参数
lambdas=[0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10]
errors_train,errors_val=[],[]
for lm in lambdas:
    theta=trainLinearReg(X_norm,y,lm)   #计算训练集和验证集不同正则化参数的代价
    errors_train.append(costReg(theta,X_norm,y,0))
    errors_val.append(costReg(theta,Xval_norm,yval,0))

plt.figure(figsize=(8,5))   #设置图的大小
plt.plot(lambdas,errors_train,label='Train')    #绘制训练集代价
plt.plot(lambdas,errors_val,label='Cross Validation')   #绘制验证集代价
plt.legend()    #添加图例
plt.xlabel('lambda')    #添加坐标名称
plt.ylabel('Error')
plt.grid()  #添加网格线
plt.show()
print(lambdas[np.argmin(errors_val)])   #选出交叉验证代价最小的是正则化参数

#计算测试误差
theta = trainLinearReg(X_norm, y, 3)
print(costReg(theta, Xtest_norm, ytest, 0))

直接对原始数据进行线性回归，得到如下效果图和学习曲线，可以看出模型存在高偏差问题，欠拟合，随着样本数量增加，训练误差和验证误差之间的差距不大且基本维持稳定。


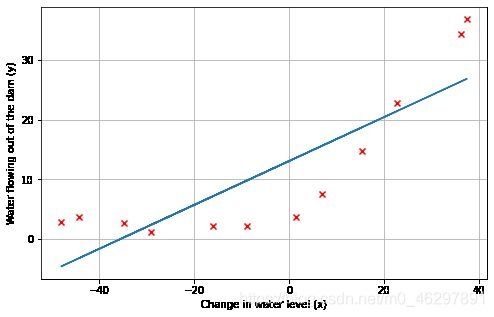
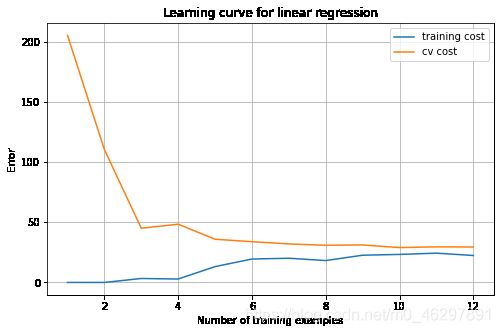
为了解决欠拟合问题，尝试引入更多特征，原始特征拓展得到多项式特征，训练得到如下效果图和学习曲线。此时模型拟合效果较好，但可能存在高方差问题，模型过拟合，训练误差很小，而验证误差较大，且存在上升趋势。


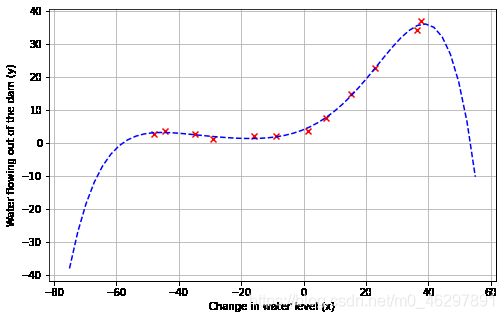
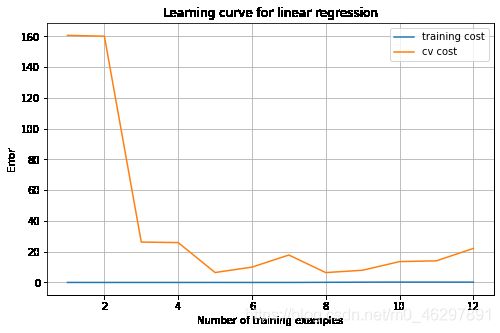
为了解决过拟合问题，对模型进行正则化。选择合适的正则化参数，以λ为横轴，绘制训练误差和验证误差的曲线如图，当λ=3时，验证误差最小，为理想的正则化参数，此时计算测试误差为4.755。

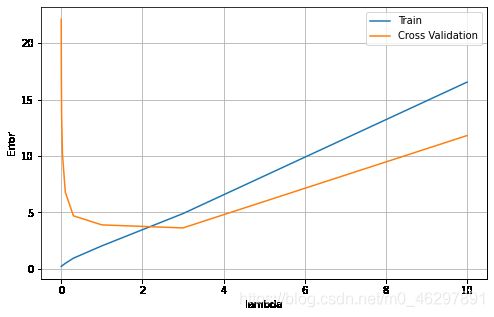
（结语个人日记：最近头发掉得有点多，真实担心自己是不是脱发辽（捂脸），开始认真考虑以后洗发水用霸王。话说B站真得神奇，竟然在上面找到了爸爸喜欢的戏曲，谁能想到大晚上11点还能有人在B站看戏曲呢，是本人在边筛选边帮爸爸下载没错了，urlgot网站也是很方便的下载辅助工具噢，可以直接复制链接下载，也不用进行格式转换。）