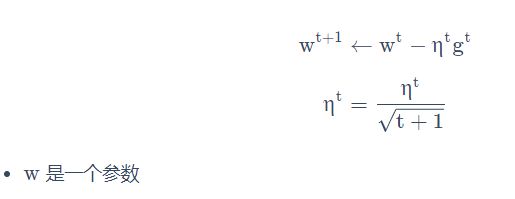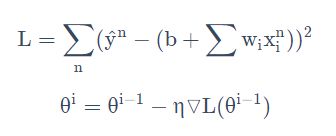李宏毅 梯度下降
梯度下降法
在回归问题的第三步中,需要解决下面的最优化问题:

这里的parameters是复数,即 θ指代一堆参数,比如上篇说到的 w 和 b 。
我们要找一组参数 θ ,让损失函数越小越好,这个问题可以用梯度下降法解决:
假设 θ有里面有两个参数 θ1,θ2 随机选取初始值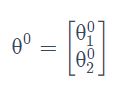
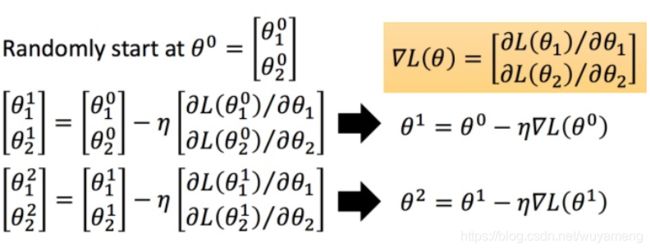
然后分别计算初始点处,两个参数对 L的偏微分,然后 θ0减掉 η乘上偏微分的值,得到一组新的参数。同理反复进行这样的计算。黄色部分为简洁的写法,▽L(θ)即为梯度。
η 叫做Learning rates(学习速率)
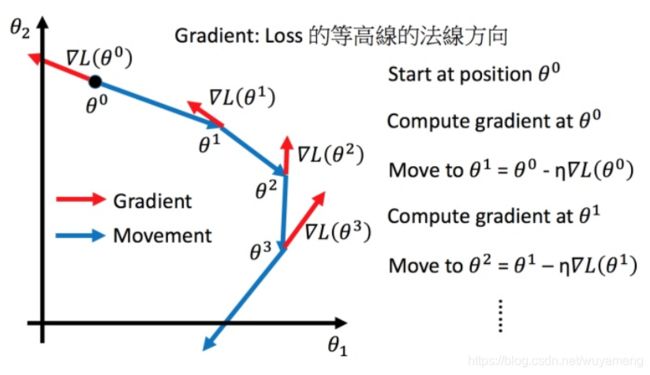
上图举例将梯度下降法的计算过程进行可视化。
Tip1:调整学习速率
小心翼翼地调整学习率
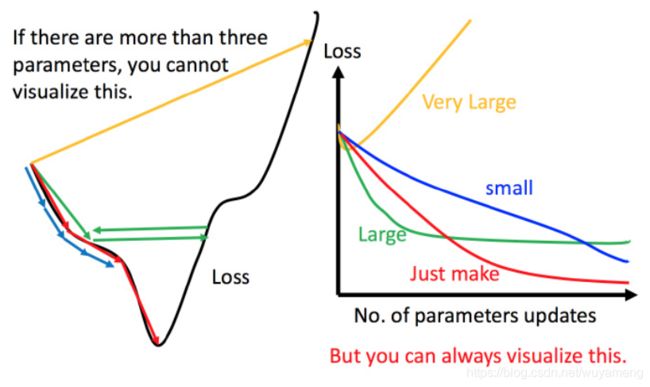
上图左边黑色为损失函数的曲线,假设从左边最高点开始,如果学习率调整的刚刚好,比如红色的线,就能顺利找到最低点。如果学习率调整的太小,比如蓝色的线,就会走的太慢,虽然这种情况给足够多的时间也可以找到最低点,实际情况可能会等不及出结果。如果 学习率调整的有点大,比如绿色的线,就会在上面震荡,走不下去,永远无法到达最低点。还有可能非常大,比如黄色的线,直接就飞出去了,更新参数的时候只会发现损失函数越更新越大。
虽然这样的可视化可以很直观观察,但可视化也只是能在参数是一维或者二维的时候进行,更高维的情况已经无法可视化了。
解决方法就是上图右边的方案,将参数改变对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的非常慢;学习率太大(绿色的线),损失函数下降很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。
自适应学习率
举一个简单的思想:随着次数的增加,通过一些因子来减少学习率
学习率不能是一个值通用所有特征,不同的参数需要不同的学习率
Adagrad 算法
每个参数的学习率都把它除上之前微分的均方根。解释:
Adagrad举例
下图是一个参数的更新过程
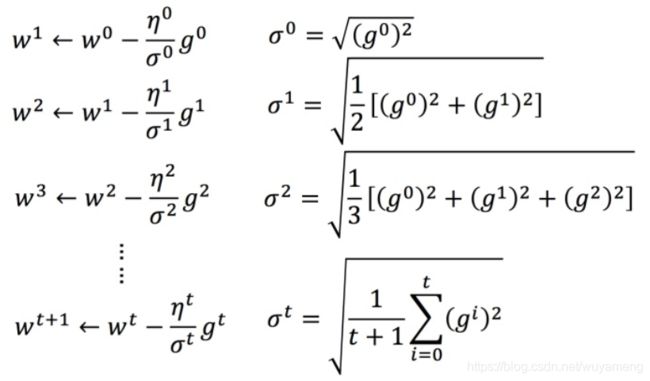
将 Adagrad 的式子进行化简:
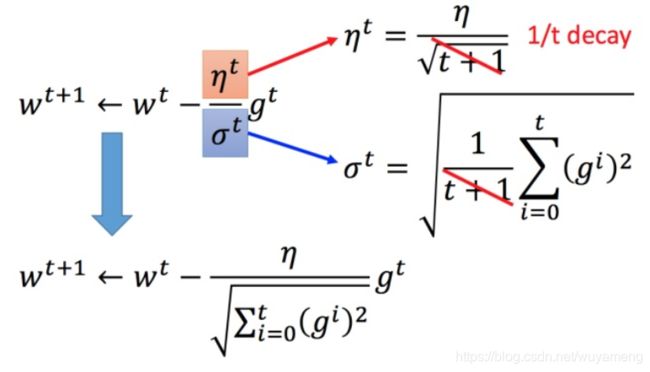
Adagrad 存在的矛盾?
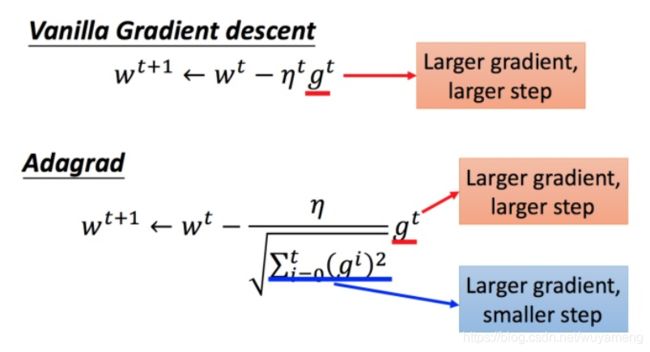
在 Adagrad 中,当梯度越大的时候,步伐应该越大,但下面分母又导致当梯度越大的时候,步伐会越小。
下图是一个直观的解释:

下面给一个正式的解释:
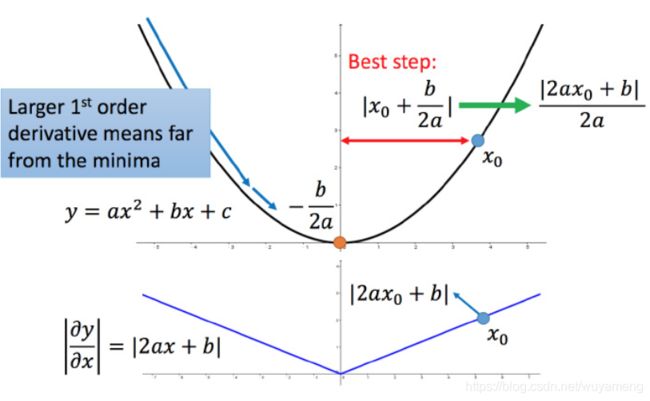
比如初始点在 x0,最低点为 -b/2a,最佳的步伐就是 x0x0 到最低点之间的距离 ∣x0+b/2a∣ ,也可以写成 ∣(2ax0+b)/2a∣.而刚好 ∣2ax0+b∣就是方程绝对值在 x0这一点的微分。
这样可以认为如果算出来的微分越大,则距离最低点越远。而且最好的步伐和微分的大小成正比。所以如果踏出去的步伐和微分成正比,它可能是比较好的。
结论1-1:梯度越大,就跟最低点的距离越远。
这个结论在多个参数的时候就不一定成立了。
多参数下结论不一定成立
对比不同的参数
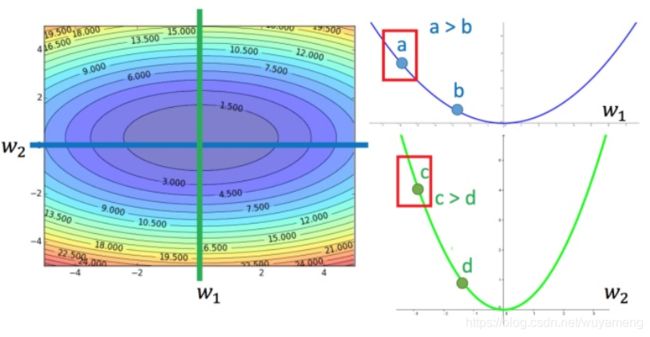
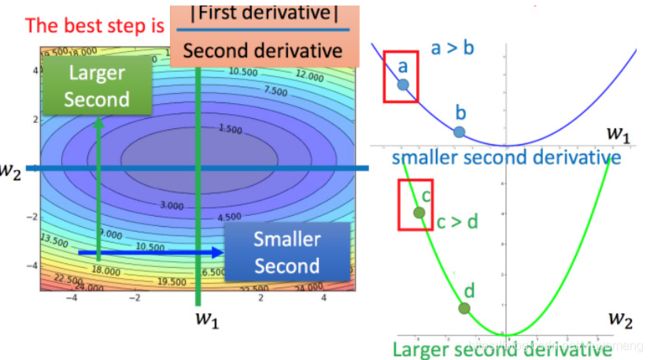
上图左边是两个参数的损失函数,颜色代表损失函数的值。如果只考虑参数 w1,就像图中绿色的线,得到右边上图结果;如果只考虑参数 w2,就像图中蓝色的线,得到右边下图的结果。确实对于 a 和 b,结论1-1是成立的,同理 c 和 b 也成立。但是如果对比a和 c,就不成立了,c 比 a 大,但 c 距离最低点是比较近的。
所以结论1-1是在没有考虑跨参数对比的情况下,才能成立的。所以还不完善。
之前说到的最佳距离 ∣(2ax0+b)/2a∣,还有个分母 2a 。对function进行二次微分刚好可以得到:
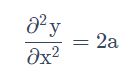
所以最好的步伐应该是:

即不止和一次微分成正比,还和二次微分成反比。最好的step应该考虑到二次微分:
Adagrad 进一步的解释
再回到之前的 Adagrad
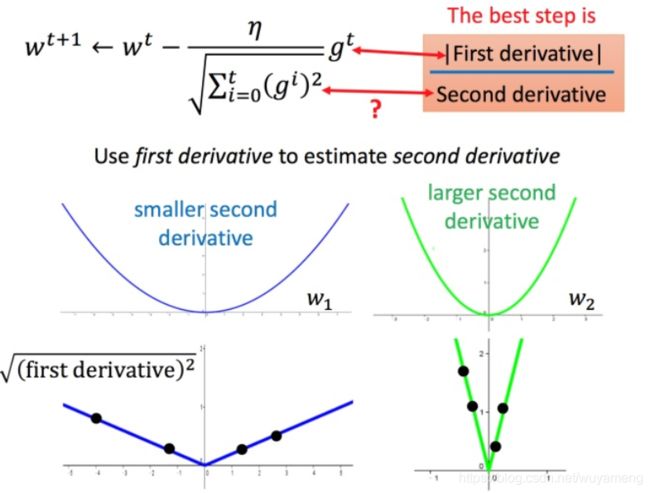
对于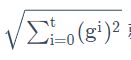 就是希望再尽可能不增加过多运算的情况下模拟二次微分。(如果计算二次微分,在实际情况中可能会增加很多的时间消耗)
就是希望再尽可能不增加过多运算的情况下模拟二次微分。(如果计算二次微分,在实际情况中可能会增加很多的时间消耗)
Tip2:随机梯度下降法
损失函数不需要处理训练集所有的数据,选取一个例子
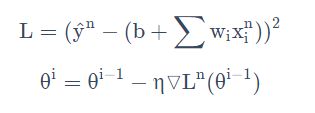
此时不需要像之前那样对所有的数据进行处理,只需要计算某一个例子的损失函数Ln,就可以赶紧update 梯度。
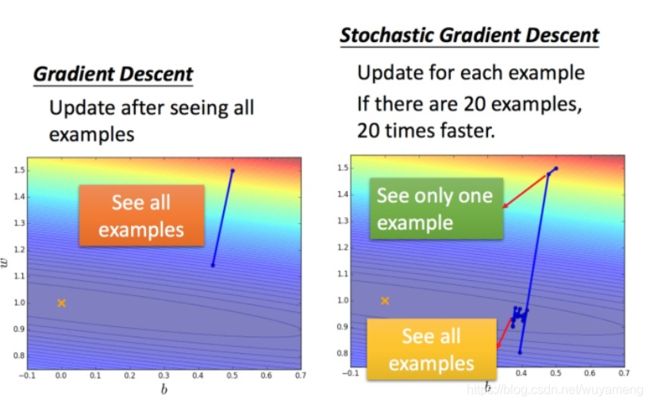
常规梯度下降法走一步要处理到所有二十个例子,但随机算法此时已经走了二十步(每处理一个例子就更新)
Tip3:特征缩放
比如有个函数: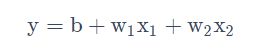 两个输入的分布的范围很不一样,建议把他们的范围缩放,使得不同输入的范围是一样的。
两个输入的分布的范围很不一样,建议把他们的范围缩放,使得不同输入的范围是一样的。
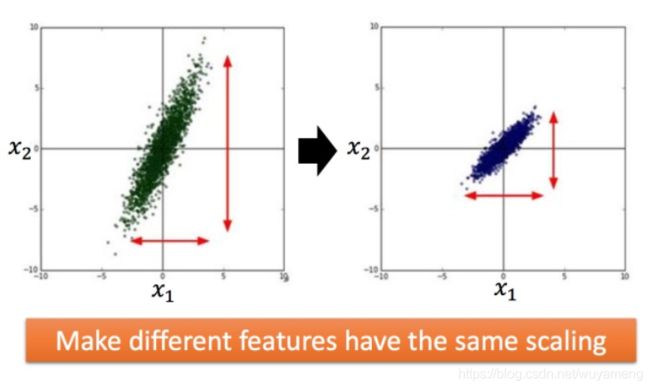
为什么要这样做?
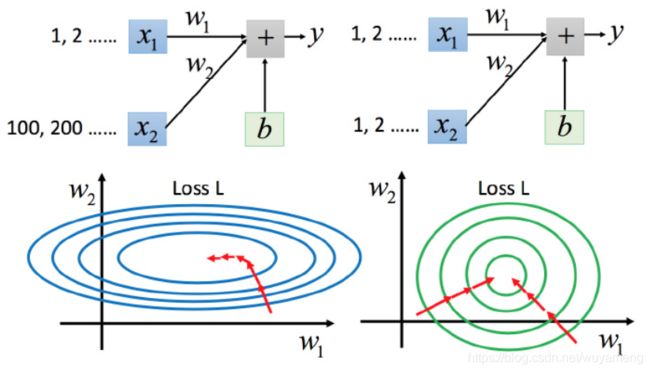
上图左边是 x1的scale比 x2要小很多,所以当 w1和 w2做同样的变化时,w1对 y 的变化影响是比较小的,x2对 y 的变化影响是比较大的。
坐标系中是两个参数的error surface(现在考虑左边蓝色),因为 w1 对 y的变化影响比较小,所以 w1对损失函数的影响比较小,w1对损失函数有比较小的微分,所以 w1方向上是比较平滑的。同理 x2对 y的影响比较大,所以 x2对损失函数的影响比较大,所以在 x2方向有比较尖的峡谷。
上图右边是两个参数scaling比较接近,右边的绿色图就比较接近圆形。
对于左边的情况,上面讲过这种狭长的情形不过不用Adagrad的话是比较难处理的,两个方向上需要不同的学习率,同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。左边的梯度下降并不是向着最低点方向走的,而是顺着等高线切线法线方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也是比较有效率。
怎么做缩放?
方法非常多,这里举例一种常见的做法:
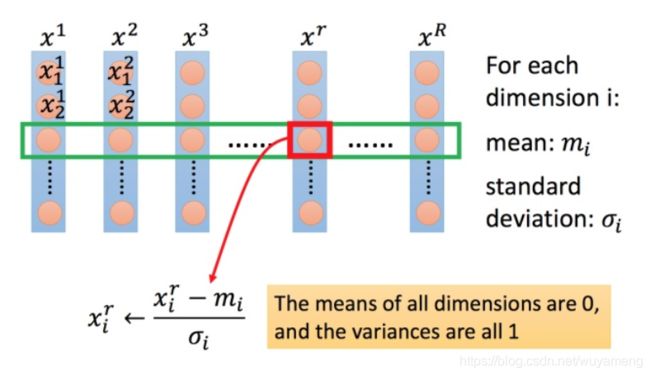
上图每一列都是一个例子,里面都有一组特征。
对每一个维度 i(绿色框)都计算平均数,记做 mimi;还要计算标准差,记做 σi然后用第 r个例子中的第 i 个输入,减掉平均数 mim i,然后除以标准差 σi,得到的结果是所有的维数都是 0,所有的方差都是 1
梯度下降的理论基础
问题
当用梯度下降解决问题:
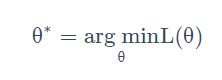
每次更新参数 θ,都得到一个新的 θ,它都使得损失函数更小。即:
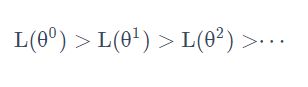
上述结论正确吗?
结论是不正确的。。。
数学理论
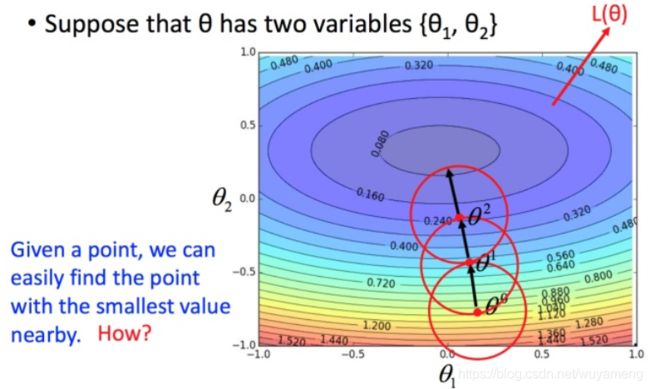
比如在 θ0处,可以在一个小范围的圆圈内找到损失函数细小的 θ1,不断的这样去寻找。
接下来就是如果在小圆圈内快速的找到最小值?…(数学推导没看了)
李宏毅 机器学习http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML20.html
https://datawhalechina.github.io/leeml-notes/#/chapter6/chapter6?id=adagrad-%e6%98%af%e4%bb%80%e4%b9%88%ef%bc%9f