Mathematica,亮瞎你的双眼
总有大一的童鞋抱怨:“高数,蓝瘦,香菇。”
那么,如何才能不挂在高数这棵“高树”上?又能较轻松地把握高数的精髓呢?
你若在百度里输入“学好高数”四字,各种建议多达千万条。
而作为一名大学数学教师的我,定会脱口而出:“请借Mathematica 一臂之力吧。”
Mathematica 是何等神器?
我给各位小朋友简单科普几句:Mathematica是一款科学计算软件,由英国数学家、物理学家和计算机学家史蒂芬·沃尔弗拉姆(Stephen Wolfram)博士开发和发行,Mathematica的很多功能在相应领域内处于世界领先地位,它也是使用最广泛的数学软件之一,它和 Matlab、Maple并称为三大数学软件。
我给各位小朋友举几个高数中简单的算例,来一展Mathematica 的强大威力。
1、利用 Mathematica 软件,验证习题答案的正误。
Mathematica代码:
In[1]:=Limit[(1+x^2)^Cot[x]^2,x->0]
Out[1]:=e
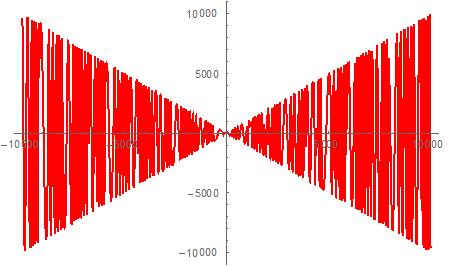
2、函数y=xcosx在定义域内是否有界?利用Mathematica软件作图可使学生的观念由似是而非到清晰正确:无界!
▲In[1]:=Plot[x*Cos[x],{x,-100,100}]
▲In[2]:=Plot[x*Cos[x],{x,-10000,10000}]
3、借助Mathematica软件,利用三维图形可方便地使学生建立空间想象,改善了黑板作图过程缓慢和准确度不高的局限。
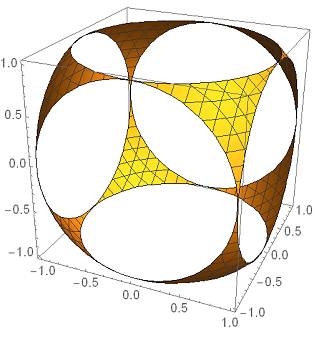
如绘制x²+y²+z²=2, 其中x,y,z属于区间[-1,1].
Mathematica代码:
In[1]:=ContourPlot3D[x^2+y^2+z^2==2,{x,-1,1},{y,-1,1},{z,-1,1}]
Out[1]:=
4、利用Mathematica软件求下列隐函数的一阶导数dy/dx。
![]()
Mathematica代码:
In[1]:= F[x_,y_]:=1-x Exp[y]-y;
Fx=D[F[x,y],x];
Fy=D[F[x,y],y];
-Fx/Fy
Out[1]:= -e^y/(1+xe^y)
5、Mathematica软件也可以亮瞎你的双眼,^_^。
Mathematica代码:
In[1]:=LogPolar[x_,y_]:={Log[Sqrt[x^2+y^2]],ArcTan[x,y]}
ImageTransformation[img,LogPolar[#[[1]],#[[2]]]&,DataRange->{{-Pi,Pi},{-Pi,Pi}}]
Out[1]:=
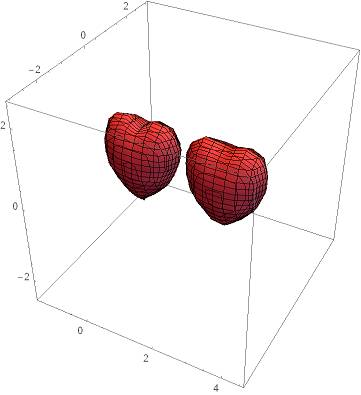
6、Mathematica 软件也可以助你尽快脱离单身汪的日子。
Mathematica代码:
In[1]:=ContourPlot3D[{(x^2+9/4 y^2+z^2-1)^3-x^2*z^3-9/80 y^2 z^3==0,((x-2.5)^2+9/4y^2+z^2-1)^3-(x-2.5)^2*z^3-9/80 y^2 z^3==0},{x,-1.5,4.5},{y,-3,3},{z,-2.5,2.5},PlotPoints->{3,3,3},Axes->True,ContourStyle->{RGBColor[2,0.3,0.3]}]
Out[1]:=
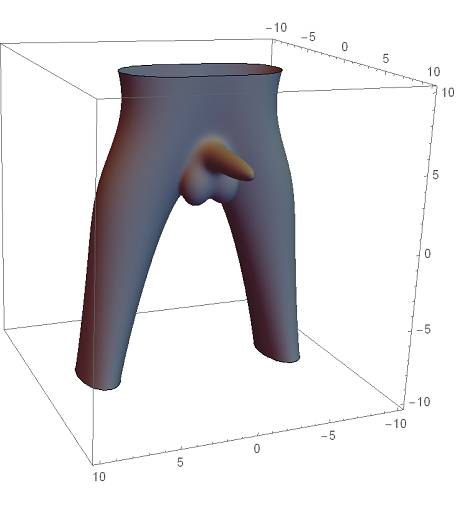
7、Mathematica软件也可以充当一回腐女,^_^。
Mathematica代码:
In[1]:=ContourPlot3D[{((((5/6+1/(4E^(z/4-2)^2)-z/90)x-(Sqrt[z^2/8+8]-z)/6-4)^2/16+(16+z)y^2/360)(((5/6+1/(4E^(z/4-2)^2)-z/90)x+(Sqrt[z^2/8+8]-z)/6+4)^2/16+(16+z)y^2/360)-1)((y-4)^2/16+2x^2+2(z-5)^2-1)((x-1)^2+(y-2)^2+(z-3)^2/2-3/4)((x+1)^2+(y-2)^2+(z-3)^2/2-3/4)==4},{x,-10,10},{y,-10,10},{z,-10,10},Mesh->None,ContourStyle->Gray]
Out[1]:=
8、Mathemtiaca 软件也可以创造高雅艺术品,一起装B吧。
Mathematica代码:
In[1]:= Clear[spiralize];
spiralize[p_,d_:10,r_:4,f_:0.8,s_:1,t_:0.005]:=Module[{m,rr=r},m=Mean@p[[1]];
Graphics[{EdgeForm[Thickness[t]],FaceForm[White],NestList[GeometricTransformation[GeometricTransformation[#,RotationTransform[rr++s°,m]],ScalingTransform[{f,f},m]]&,p,d]}]]
pts=RandomReal[{-1,1},{50,2}];
polys=MeshPrimitives[VoronoiMesh[pts],2];
Show[spiralize[#,40,5,0.85]&/@polys]
Out[1]:=
让我们荡起双桨,安装Mathematica,恋上Mathematica。