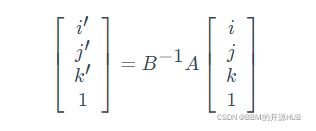医学影像中的坐标系
坐标系是一种识别点位置的方法。在医学界,成像应用中常用的坐标系有三种:全局坐标系、解剖学坐标系和医学图像坐标系。
一:全局坐标系统
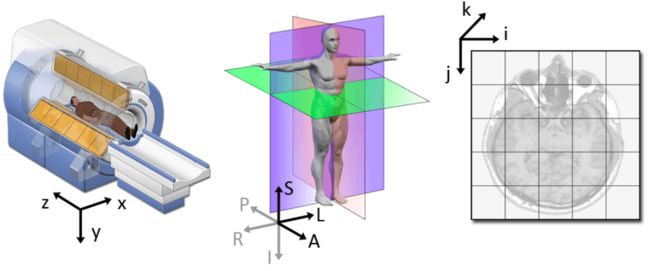
全局坐标系是一个笛卡尔坐标系,医学图像模式(如MRI扫描仪或CT)位于该坐标系中。每个医疗模式都有自己的坐标系,但只有一个全局坐标系来定义每个模式的位置和方向。
二:解剖学坐标系
医学成像技术中最重要的模型坐标系是解剖空间(也称为患者坐标系)。该空间由三个平面组成,用于描述人体的标准解剖位置:
(1)轴向平面【Axial plane】
(2)矢状面【Sagittal plane】
(3)冠状面【Coronal plane】
值得一提的是,该系统的发明是为了更好地在医生和放射科医生之间进行交流。3D 位置是沿前后(前后)和左右和上下的解剖轴定义的。从这个意义上说,所有轴的符号都指向正方向。
1、轴向平面【Axial plane】
轴向平面实际上是当您将视角置于患者上方并向下看时。根据 3D 医学图像的区域,您将观察到不同的解剖结构。对于 3D 全身扫描,您将从头部的 2D 切片开始,直到腿部结束。让我们实际上称这个视图为“顶视图”。
出于解剖学一致性的原因,靠近头部的切片称为上切片,靠近脚的切片称为下切片。
2、矢状面【Sagittal plane】
矢状面是一个侧视图,现在我们从侧面看,而不是从病人上方看。侧面可以是右侧或左侧。哪个边和哪个方向是正的,取决于坐标系!可以肯定的是,从这个视图(平面)你可以看到病人的耳朵!当您通过该轴移动时,您会看到投影的组织,如肺、骨骼。
脑部 MRI 的矢状视图如下图所示:
3、冠状面【Coronal plane】
在此视图中,我们通过患者的前面,或查看患者背部(后平面)进行遍历。
为了确保你永远不会忘记冠状平面是什么,我发现了这个可怕halloween.gif。
三:医学影像坐标系(体素空间)
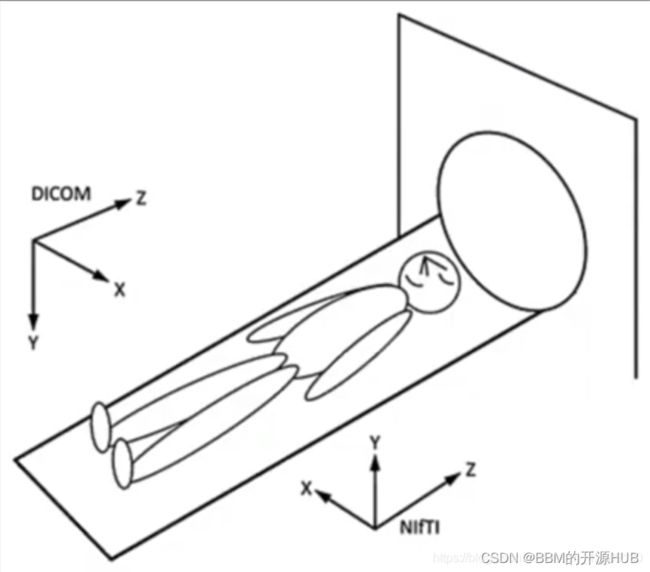
医学影像坐标系统:从左上角开始的点和单元格的3D数组/张量,类似于 2D 的 RGB 相机。i轴向右增加(宽度),j轴向底部增加(高度),k轴向后增加(第三个类似于卷积网络的特征图)。
除了每个体素(ijk)的强度值外,坐标的原点(即 MRI)和间距都存储在医学图像的元数据中(dicom 标签,Nifti的头文件,你可以命名它。 )
体素间距基本上是对应于 3D 区域的体素的实际大小以及两个体素之间的距离。
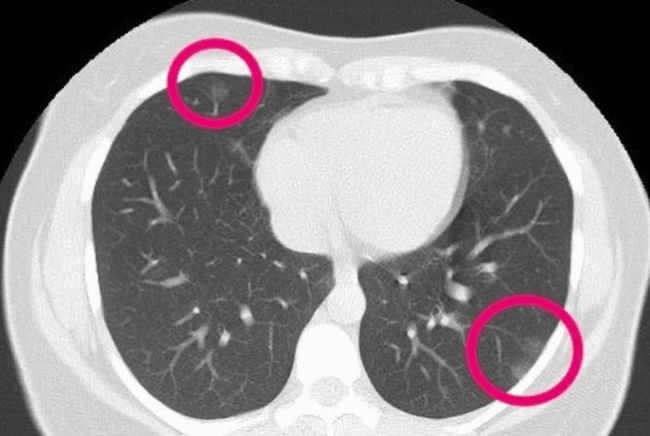
例如,如果我们想测量癌症肿瘤细胞的体积,这很重要。
请注意,可以重新采样到更大的体素大小以减小医学图像的大小。这可以理解为对信号的下采样操作。医学人会说这样我们保持视野不变,但我们简单说这是体素空间中的一种下采样技术。
注意:如果体素在所有 3 个维度上都具有相同的大小,我们称为图像各向同性,类似于 RGB 图像中的各向同性缩放。
仿射变换
它被称为著名的仿射矩阵。在仿射变换之前,让我们澄清一下什么是几何变换。几何映射/变换是一种阐明体素强度不变的方法。
因此,根据维基百科对仿射的定义 :在几何学中,仿射变换是仿射空间的几何映射,它保留了许多属性,例如它发送点到点、线到线、平面到平面。此外,它还保留了平行线长度的比率。但是,仿射变换不一定保留线之间的角度或点之间的距离。
在数学中,为了同时表示平移和旋转,我们需要创建一个方形仿射矩阵,它比我们的空间多一维。由于我们处于 3D 空间中,因此我们需要在医学成像中使用 4D 仿射矩阵。使用仿射矩阵,我们可以通过矩阵乘法来表示任何线性几何变换(平移、旋转),如下图所示。
从一种模式转移到另一种模式
我们已经看到仿射是从体素到全局坐标的转换。事实上,仿射有一个属性是:仿射的倒数给出了从 world 到 voxel 的映射。因此,我们可以从一个医学图像的A描述的体素空间到另一个模态B的另一个体素空间。通过这种方式,两个医学图像“生活”在同一个体素空间中。
两种坐标系统的转换代码:
import scipy
def transform_coordinate_space(modality_1, modality_2):
"""
Transfers coordinate space from modality_2 to modality_1
Input images are in nifty/nibabel format (.nii or .nii.gz)
"""
aff_t1 = modality_1.affine
aff_t2 = modality_2.affine
inv_af_2 = np.linalg.inv(aff_t2)
out_shape = modality_1.get_fdata().shape
# desired transformation
T = inv_af_2.dot(aff_t1)
# apply transformation
transformed_img =
scipy.ndimage.affine_transform(modality_2.get_fdata(), T, output_shape=out_shape)
return transformed_img让我们看看如果我们将此代码应用于两个不同的 MRI 图像会发生什么:
前 3 个切片来自参考图像,接下来的 3 个切片来自我们要转换的图像,第三个是转换到全局的图像。它们都生活在同一个仿射世界中,我们可以一起想象它们,它们也具有相同的形状。
本文部分翻译了:Nikolas Adaloglou于2020-07-16 所作:
《Understanding coordinate systems and DICOM for deep learning medical image analysis》
本文所引用的图片为Nikolas Adaloglou所做。