A Survey on Neural Network Interpretability (神经网络的可解释性研究综述)

作者：Yu Zhang, Peter Tino, Ale s Leonardis, and Ke Tang
翻译：Wendy

摘要

  随着神经网络的巨大成功，人们对其黑匣子的性质也越来越关注。神经网络的可解释性影响着人们对深度学习系统的信赖。它也与许多道德问题有关，例如算法歧视。此外，可解释性是深度神经网络成为其他领域（例如药物研发和基因组学）中强大工具的重要属性。在这篇综述中，我们对神经网络的可解释性研究进行了全面的回顾。首先我们阐释了可解释性的定义，因为它已经在不同地方都有应用。然后，我们详细阐述了可解释性的重要性，并提出了一个新的分类方法，该分类方法从三个方面进行了组织：参与类型（被动与主动解释方法），解释类型及关注点（从局部解全局的可解释性）。该分类法提供了来自相关文献的论文分布的有意义的3D视图，因为其中两个维度不仅是简单的分类，还允许有序的分子分类。最后，我们总结了现有的可解释性评估方法，并根据我们的新分类法提出了可能的研究方向。
关键词：机器学习，神经网络，可解释性，综述

Ⅰ 引言

  过去的几年里，深度神经网络（DNNs）在计算机视觉、语音识别、自然语言处理和其他领域都取得了巨大的成功。它不仅打败了很多已有的机器学习方法，而且在现实的任务上表现也是最好的。由DNN提供支持的产品现已被数十亿人使用，例如人脸识别和语音识别中。DNNs已经成为很多涉及海量数据的科学领域强有力的工具，例如医学，生物信息学，和天文学。

  但是，深度学习仍然有一些明显的缺点。对于一个拥有数百万个自由参数的复杂模型（如AlexNet,6200万个参数），DNNs经常会表现出意想不到的效果。例如，即使网络可以达到最先进的功能，并且在对象识别上似乎可以很好的概括，Szegedy等人找到了一种方法，可以通过对输入图像应用某种难以察觉的变化来任意改变网络的预测。这种修改过的输入被称为“对抗范例”。Nguyen等人展示了另一种产生完全无法识别的图像（例如，看起来像白噪声）的方法。然而，DNNs以99.99%的置信度识别特点的对象。这些观察结果表明，尽管DNN 在许多任务中都能取得优异的表现，但他们的潜在机制可能与人类的机制截然不同，而且目前还没有被很好地理解。

A 可解释性的（扩展）定义

  为了打开深度神经网络的黑箱子，很多学者开始关注模型的可解释性上。尽管这个主题已经在很多文章中已经被探索了，但是目前对于可解释性的定义还没有一个统一的定义。大多数之前的作品都忽略了澄清的问题，并留下了“当你看到它时就会知道它”的说法。如果我们仔细观察，建议的定义和可解释性的动机往往是不同的，甚至是不一致的。

  之前对可解释性的一个定义是用可理解的术语向人类提供解释的能力，而术语解释本身仍然是难以捉摸的。在回顾以往文献后，我们在此基础上对“解释”和“可理解的术语”做了进一步的澄清。

  可解释性是用可理解的术语向人类提供解释的能力。其中

1. 理想情况下，解释应该是逻辑决策规则（if-then规则），或者可以转换为逻辑规则。然而，人们通常不要求以规则的形式明确解释（但只要求一些可以用来构建解释的关键元素）。
2. 可理解的术语应该来自与任务相关的领域知识（或根据任务的常识）。

  我们的定义为解释性研究提供了新的视角：（1）我们强调解释的形式，而不是特定的解释者。毕竟，解释是用某种语言来表达的，它可能是自然语言，逻辑规则，也可能是其他什么东西。最近，一种强烈的偏好被表达为解释语言尽可能接近逻辑。在实践中，人们并不是总是需要一个完整的“句子”，这允许各种解释（规则，显著性面具等）。这是对现有文献中研究方法进行分类的一个重要角度。（2）领域知识是解释构建的基本单位。随着深度学习显示出以原始形式处理数据的能力，人们用原始输入表示来解释模型变得更加困难。有了更多的领域知识，我们可以得到更多可被领域专家评估的可理解的表示。表Ⅰ列出了不同任务中常见的几种表示形式。
  我们注意到，一些研究区分了可解释性（ interpretability）和可解释性（ explainability）（或可理解性、透明度、人类模拟性等）。在本文中，我们不强调这些术语之间的细微差别。如上定义，我们将解释为可解释性的核心，并可互换地使用可解释性和可理解性。具体来说，我们关注（深度）神经网络（很少是递归神经网络）的可解释性，其目的是提供其内部工作和输入-输出映射的解释。

  在我们的定义下，Linux操作系统的源代码是可以解释的，尽管它可能对开发人员来说是压倒性的。深度决策树或高维线性模型（在可解释的输入表示之上）也是可解释的。有人可能会说它们不是可解释的。有人可能会说它们是不模拟的（即人类能够在他/她的脑海中在短时间内模拟模型从输入到输出的过程）。然而，我们声称，它们仍然是可解释的。

B 可解释性的重要性

  许多论文已经强调了对可解释性的需要，强调在缺乏可解释性可能是有害。然而，对于这样的论证，却缺乏一个条理清晰的阐述。我们把关于可解释性重要性的论点归纳为三组。

1. 高可靠性要求：虽然深度网络在一些相对较大的测试集上表现出了良好的性能，但现实环境仍然要复杂得多。由于一些意想不到的失败是不可避免的，我们需要一些方法来确保我们仍然在控制之中。深度神经网络不提供这样的选项。在实践中，它们经常被观察到在某些情况下会出现意想不到的性能下降，更不用说来自对抗性例子和潜在攻击。
     可解释性并非总是必需的，但对于有一些要求高度可靠的预测系统来说，它很重要，因为一个错误可能会导致灾难性的结果（例如，人的生命，严重的经济损失）。可解释性可以使潜在的故障更容易检测（在领域知识的帮助下），避免严重的后果。此外，它可以帮助工程师查明根本原因并提供相应的修复。可解释性并不会使模型更可靠或性能更好，但是它是可靠系统的重要组成部分。

2. 道德及法律要求：
     第一个要求是避免算法歧视。由于机器学习技术的性质，训练过的深度神经网络可能会继承训练集中的偏差，这有时很难注意到。DNNs在日常生活中使用时，会涉及到公平性问题，例如抵押贷款资格评估、信用评估、保险风险评估等。
     深度神经网络也被用于新药的发现和的设计。计算药物设计领域由传统的机器学习方法(如随机森林和广义相加模型)主导，部分原因是它们当时的高效学习算法，也因为可以对领域进行化学解释。一种新药要获得监管机构的批准，如食品和药物管理局(FDA)，还需要具有可解释性。除临床试验结果外，通常还需要研究其生物学机制。医疗设备也是如此。
     另一个关于可解释性的法律要求是[25]中的“解释权”。根据欧盟一般数据保护条例(GDPR)第22条，人们有权不受自动决定的影响，这将产生法律效果或类似的重大影响，他或她。数据控制器应保障数据所有者获得人工干预、表达其观点和对该决定提出异议的权利。如果我们不知道网络是如何做出决定的，就没有办法确保这些权利。

3. 科学的使用方法：
     深度神经网络正在成为科学研究领域的强大工具，这些领域的数据可能具有复杂的内在模式(如基因组学，天文学，物理学，甚至社会科学)。“科学”一词来源于拉丁语“scientia”，意思是“知识”。当深度网络达到比旧模型更好的性能时，它们一定发现了一些未知的“知识”。可解释性是揭示它的一种方式。

C 相关工作及贡献

  已经有人试图总结神经网络可解释性的技术。然而，它们大多只提供基本的分类或枚举，没有明确的分类法。Lipton指出，可解释性这一术语并没有很好的定义，在不同的研究中往往有不同的含义。然后，他对可解释性研究中的需要(如信任、因果关系、公平决策等)和方法(事后解释)进行了简单的分类。Doshi-V elez和Kim对可解释性的定义和评价进行了讨论，这启发了我们制定更严格的定义，并在此基础上对现有的方法进行分类。Montavon等人将解释的定义局限于特征重要性(在其他地方也称为解释向量)，并审查了通过网络解释学习到的概念和个人预测的技术。它们的目的不是给出一个全面的概述，只是包括一些有代表性的方法。Gilpin等人将这些方法分为三类:解释数据处理、解释数据表示和解释产生网络。在这个分类下,线性代理模型法和rule-extraction法同样视为代理方法,没有注意到它们之间的许多差异(前者是局部的一个方法,而后者通常是全局和他们的解释是不同的,我们将看到它在我们的分类中)。Guidotti等人考虑了所有的黑盒模型(包括树集合、支持向量机等)，并基于四个维度(可解释性问题的类型、解释器的类型、黑盒模型的类型和数据类型)给出了细粒度的分类。然而，他们把决策树、决策规则、显著性掩码、敏感性分析、激活最大化等作为解释。在我们看来，有些是特定类型的解释，而有些是用于产生解释的方法。Zhang和Zhu回顾了计算机视觉领域中理解网络中间层表示或学习具有可解释表示的网络的方法。

  本综述的贡献如下:

1. 我们在参考文献[15]的基础上进一步定义了可解释性。在这个定义中，我们强调解释的类型(或格式)(例如，规则形式，包括决策树和决策规则集)。在我们提出的分类中，这是一个重要的维度。以往的论文通常将现有的方法组织成各种孤立的(在很大程度上)解释器(如决策树、决策规则、特征重要性、显著性图等)。
2. 我们分析了可解释性的真实需求，并将其归纳为3组:可解释性作为系统的重要组成部分，应该是高度可靠的，伦理或法律要求，可解释性提供工具，以增强相关科学领域的知识。相比之下，之前的调查仅仅通过提供一些黑箱模型可能是危险的情况来显示可解释性的重要性。
3. 我们提出了一个包含三个维度的新分类法(被动和主动方法，解释的格式，局部-半局部-全局可解释性)。请注意，虽然在以前的文献中已经讨论了分类法的许多成分，但它们要么是在完全不同的上下文中提到的，要么是相互纠缠在一起的，因此不能作为适当的分类标准(例如，我们的最后两个正交维度)。据我们所知，我们的分类法为现有的方法提供了最全面、最清晰的分类。

  额外的优点:我们的分类可以在一个有意义的3D视图中可视化，并提供更多的洞见，以了解不同尝试的可解释性深层网络是如何相关的，也为填补可解释性研究的空白提供了建议(见图2)。

D 综述组织结构

  综述的其余部分组织如下。在第二节中，介绍了我们提出的网络解释方法的分类。该分类包括三个维度:被动与主动方法、解释类型和全局与局部可解释性。沿着第一个维度，我们将方法分为两组，被动方法(第三节)和主动方法(第四节)。在每一节中，我们遍历剩下的两个维度(不同种类的解释，以及它们是局部的、半局部的还是全局的)。第五节对可解释性的评价作了简要的总结。最后，我们在第6节对本文进行总结。

Ⅱ 分类

  我们提出了一种新的分类法，它有三个维度(见图1):(1)被动方法和主动方法维度，(2)产生解释的类型/格式，以及(3)分别从局部解释性维度到全局解释性维度。第一个维度是范畴性的，有两种可能的价值:被动解释和主动解释性干预。根据需要改变网络结构或优化过程，对现有的方法进行了划分。被动解释过程从一个训练过的网络开始，所有的权值都已经从训练集学习到。然后，这些方法尝试提取逻辑规则或提取一些可理解的模式。而主动方法则需要在训练前做一些改变，例如引入额外的网络结构或修改训练过程。这些修改促使网络变得更加可解释(例如，更像一个决策树)。这种积极干预最常见的形式是正规化。

  与以前的综述相比，其他两个维度允许序数值。例如，之前提出的解释器的维度类型产生了决策树、决策规则、特征重要性、敏感性分析等子类别。然而，这些预先识别的解释器之间并没有明确的联系(决策树和特征重要性之间的关系是什么)。相反，我们的第二个维度是解释的类型/格式。通过考察不同方法产生的各种解释，我们可以观察到它们在明确程度上的差异。逻辑规则提供了最清晰和明确的解释，而其他类型的解释可能是隐性的。例如，显著性映射本身只是特定输入上的掩码。通过观察显著性图，人们构建了一种解释:“模型之所以做出这种预测，是因为它关注于这一极具影响力的部分和那一部分(输入)。”希望这些部分对应于一些领域可以理解的概念。严格地说，隐性解释本身并不是完整的解释，需要进一步的人为解释，通常是人们看到隐性解释时自动进行的。我们在这里认识到四种主要的解释类型，逻辑规则，隐含语义，归因和例子解释，按解释力的降低顺序排列。类似的讨论可以在以前的文献中找到，例如，Samek 等人有一个关于“解释类型”的小分段讨论(包括解释学习到的表征，解释个人预测等)。然而，它与另一个独立的维度混合在一起，我们现在将介绍它。

  最后一个维度,从局部到全局可解释性(w.r.t.输入空间),已经成为很常见的在最近的文件(例如,[15],[21],[30]),全局可解释性意味着能够理解当地的总体决策逻辑模型和可解释性关注个人预测的解释。然而，在我们提出的维度中，存在一个过渡，而不是一个硬划分之间的全局和局部可解释(即半局部可解释)。局部解释通常利用目标输入的信息(例如，其特征值、梯度)。但全局解释试图将输入的范围尽可能广泛(例如，规则学习中的顺序覆盖，特征重要性排序的边际贡献)。这一观点也被几种半局部解释方法所支持。也有人试图以一种自下而上的方式将本地解释融合到全局解释中。

  为了帮助理解后两个维度，表II列出了分类法下不同子类别产生的典型解释示例。(第1行)当考虑将规则作为本地可解释性的解释时，一个例子是提供只适用于给定输入x(i)(及其相关输出ˆy(i))的规则解释。其中一个解决方案是找出(通过干扰输入特性并查看输出如何变化)最小的特性集xk…xl的存在支持预测ˆy(i)。类似地，xm的特性…可以找到不应该存在的xn(更大的值)，否则ˆy(i)将发生变化。那么x(i)的解释规则就可以构造为“这是因为xk…”xl 出现而且 xm…xnare缺席x(i)被归类为ˆy(i) "。如果一个规则不仅对输入x(i)有效，而且对它的“邻域”有效，我们就得到了一个半局部可解释性。如果从原始网络中提取一个规则集或决策树，就可以解释整个网络的一般功能，从而提供全局可解释性。(第2行)当涉及到解释隐藏语义时，一个典型的例子(全局的)是可视化隐藏神经元最敏感的模式。这样就可以提供有关网络内部工作的线索。我们也可以采取更积极的方法，让隐藏的神经元更容易理解。由于高层隐藏神经元可能会学习一些难以解释的混合模式，Zhang等人引入了一个损耗术语，使高层滤波器要么产生一致的激活映射(在不同输入之间)，要么保持不活动(当没有看到某个特定模式时) 。实验表明，这些过滤器更容易解释(例如，可以发现一个过滤器是由动物的头部激活的)。(第3行)归因作为解释通常提供局部可解释性。想想一个动物分类任务，输入特征是输入图像的所有像素。归类允许人们看到图像的哪个区域(像素)对分类结果的贡献最大。可以计算归因，例如，根据输入特征(即所有像素)或一些变量进行敏感性分析。对于全局可解释性的归因，深度神经网络通常不能具有像线性模型y = w*x + b中的系数w这样简单的归因，它直接显示了特征的全局重要性。Kim等人没有把注意力集中在输入特征(像素)上，而是对“概念”的归属感兴趣(例如，斑马的预测对条纹的存在有多敏感)。在网络隐藏层的空间中，条纹的概念用分隔有条纹和非条纹训练实例的平面的法向量来表示。因此，可以计算(斑马的)预测对概念(条纹的存在)的敏感性，从而具有某种形式的全局可解释性。(第4行)有时研究人员通过展示其他提供类似网络功能的已知例子来解释网络预测。为了解释单个输入x(i)(局部可解释性)，我们可以在网络的隐含层层中找到一个与x(i)最相似的例子。这种解释示例的选择也可以通过测试如果从训练集中删除某个示例，x(i)的预测将受到多大影响来完成。为了通过示例提供全局可解释性，一种方法是在网络中添加一个(可学习的)原型层。原型层迫使网络根据输入和被学习原型之间的接近程度做出预测。那些学习和可解释的原型可以帮助解释网络的整体功能。

  通过上面介绍的三维，我们可以在三维视图中可视化现有可解释性论文的分布(图2只提供了一个二维快照，我们鼓励读者访问在线互动版本以获得更好的演示)。表III是对所有可解释性方法的另一种表示，这些方法有助于快速导航。

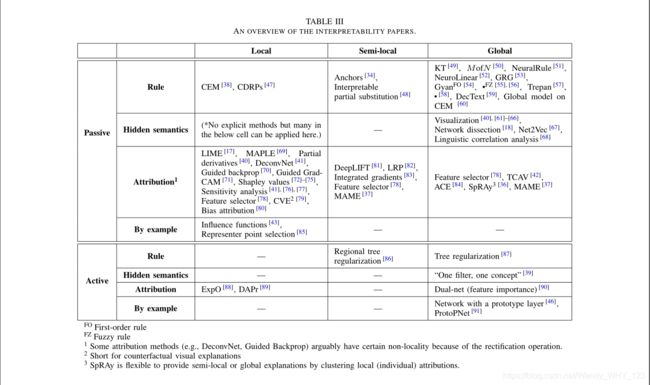
  在下面几节中，我们将沿着每个维度浏览表III。第一个维度分为两个部分，被动方法(第三节)和主动方法(第四节)。然后我们根据第二个维度(解释类型)将每个部分展开为几个小部分。在每个小节中，我们分别介绍(半)局部和全局的可解释性方法。

Ⅱ 对训练过的网络的被动解释

  现有的网络解释方法大多是被动的方法。他们试图理解已经训练过的网络。我们现在根据它们产生的解释类型(即第二维度)来介绍这些方法。

A 被动，规则作为解释

  人们普遍认为逻辑规则是可解释的，并且有悠久的研究历史。 规则提取方法提供了全局解释，因为它们只从目标模型中提取单个规则集或决策树。下面我们将介绍一些产生(半)局部规则形式解释的方法(第III-A1节)，下面是全局方法(第III-A2节)。另一件需要注意的事情是，尽管规则和决策树(以及它们的提取方法)可能非常不同，但我们在这里没有明确区分它们，因为它们提供了类似的解释(决策树可以扁平化为决策规则集)。规则的基本形式是
   If P, then Q.
  其中P称为先行件（原因），Q称为随后事件（结果），在我们的语境中是网络的预测(如类标签)。P通常是几个输入特征的条件组合。对于复杂模型，解释规则可以是命题规则、一阶规则或模糊规则等其他形式。

被动，规则作为解释，(半)局部

  根据我们的分类，这类方法关注于训练过的神经网络和特定的输入(或一小组输入)，并产生一个逻辑规则作为解释。Dhurandhar等人通过找出应该最少且充分存在的特征以及应该最少且必然不存在的特征来构建局部规则解释。简而言之，解释是这样的:“如果一个输入x被分类为y类，那是因为特征fi，…， fk出现和功能fm，…fp缺席”。这是通过寻找小的稀疏扰动来实现的，这些扰动足以确保它自己的预测(或者在应用到目标输入时将改变预测)。(他们还扩展了这个方法，以学习一个全局可解释模型，例如，一个决策树，基于自定义特征，从上面的局部解释创建。)Wang等人提出了另一种局部可解释性方法，为每个输入识别网络的关键数据路由路径(CDRPs)。在卷积神经网络中，每个核产生一个特征映射，该特征映射将作为通道被送入下一层。Wang等人将每一层上的每个输出通道与门(非负权值)相关联，这表示该通道有多关键。然后对这些门权值进行优化，这样当它们与相应的输出通道相乘时，网络仍然可以做出与原始网络相同的预测(在给定的输入上)。重要的是，权重被鼓励是稀疏的(大多数接近于零)。然后，通过首先识别关键节点，即与正门相关联的中间核，就可以为每个输入识别cdrp。我们可以探索并赋予关键节点意义，使关键路径成为局部解释。然而，由于原始论文并没有进一步探讨CDRPs表示，这可能是人类无法理解的，它仍然是一个激活模式，而不是一个真正的解释。

  我们还可以提取覆盖一组输入而不是单个输入的规则。Ribeiro等人提出锚是局部足够精确(半)的if-then规则。换句话说，如果一个规则适用于一组相似的例子，他们的预测(几乎)总是相同的。这类似于我们将在第三节- c部分介绍的归因方法LIME。然而，它们在产生的解释方面是不同的(LIME为个别例子产生归因)。Wang等人[48]试图找到覆盖输入空间某个子集的网络的可解释部分替换(规则集)。根据子集的大小，这种替换可以在不影响或降低模型精度的情况下完成。

被动的、规则作为解释的、全局的

  大多数时候，我们希望对网络有某种形式的整体解释，而不是它在单个点上的局部行为。我们再次将这些方法分为两组。一些规则提取方法利用网络特定的信息，如网络结构或学习的权值。这些方法在以前的文献中称为分解方法。而其他方法则将网络视为一个黑匣子，只使用它为经典规则学习算法生成训练示例。它们被称为教学方法。

1.全局方法:分解方法通过观察网络中的连接来生成规则。由于许多方法都是在深度学习时代之前开发的，它们大多是为经典的全连接前馈网络设计的。考虑全连接网络的单层设置(只有一个输出神经元)

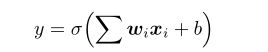
  其中σ是一个 激活函数(通常是sigmoid， σ(x) = 1/(1+ e−x))， w是可训练的权值，x是输入向量，b是偏置项(通常称为阈值θ是早期时间，这里b可以解释为θ的负值)。规则提取的核心是搜索使y接近1的属性xi的特定值(或范围)的组合。这只有在我们处理小型网络时才容易处理，因为随着属性的数量和每个属性的可能值的增加，搜索空间的大小将很快增长到天文数字。假设我们有n个布尔属性作为输入，每个属性都可以为真或假或在先行词中不存在，那么有O(3n)个组合要搜索。因此，我们需要一些搜索策略。

  最早的方法之一是KT算法。KT算法首先根据其对应权值的符号将输入属性分为pos-atts (positive attributes)和negative -atts两组。假设激活函数是 sigmoid,所有神经元booleanized为true(如果足够接近1)或false(接近0)。然后,所有的组合选择pos-atts如果自行组合可以使y是正确的(大于一个预定义的阈值β不考虑neg-atts),例如,{x1, x3}和σ(P我∈{1,3}wixi + b) >β。最后，它考虑了negative -atts。对于上述每一个pos-atts组合，它发现negative -atts的组合(例如，{x2, x5})，当不存在时，从所选pos-atts和未选择的negative -atts计算出的输出仍然为真。即σ(P i∈Iwixi+b) > β，其中i = {x1, x3}∪{neg-atts} \ {x2, x5}。然后，提取的规则可以由组合I组成，并具有输出类1。在我们的示例中，转换后的规则是

  类似地，这个算法可以生成0类的规则(先搜索负att，然后添加pos-att)。为了适用于多层网络的情况，它首先逐层生成规则，然后重写它们，忽略隐藏的神经元。在复杂度方面，KT算法通过区分pos-atts和negative -atts (posatts为真或缺，negative -atts为假或缺)，将搜索空间缩小到O(2n)。它还限制了前因后果中属性的数量，这可以进一步降低算法的复杂性(可能会丢失一些规则)。

  Towell和Shavlik[50]专注于另一种“M-of-N”风格的规则。这种规则不强调输入属性的个人重要性

如果N个表达式中有M个为真，那么为Q。

  该算法有两个显著特点。第一种是链接(权值)聚类，并在聚类中为它们重新分配平均权值。另一个特点是网络简化(消除不重要的集群)和再训练。与子集搜索算法的指数复杂度相比，M-of-N方法由于其特殊的规则形式，其复杂度近似为三次。

  NeuroRule 引入了提取规则的三步流程:(1)训练网络并进行修剪;(2)离散(聚类)隐藏神经元的激活值;(3)分层提取规则并重写(与之前的方法类似)。NeuroLinear 对neurorrule方法做了一点改变，允许神经网络有连续的输入。Andrews等人和Tickle等人对1998年以前的规则提取技术进行了很好的总结。

2.教学方法:通过将神经网络视为一个黑匣子，教学方法(或两者的混合)可以直接从网络生成的示例中学习规则。它本质上是一个传统的规则学习或决策树学习问题。对于规则集学习，我们有顺序覆盖框架(即一个接一个地学习规则)。对于决策树，有许多经典算法，如CART 和C4.5。从神经网络中提取决策树的实例可以在参考文献[57]-[59]中找到。

  Odajima等人遵循了NeuroLinear的框架，但使用了贪婪形式的顺序覆盖算法来提取规则。据报道，它可以提取更简洁、更精确的规则。Gyan方法比提取命题规则更进一步。通过上述方法得到命题规则后，Gyan使用最小广义推广(LGG)方法从中生成一阶逻辑规则。也有一些方法试图从训练过的神经网络中提取模糊逻辑。主要的区别是引入了语言术语的隶属功能。一个示例规则是

其中， high是一个模糊术语，表示为数字上的模糊集。

B 被动的，隐藏的语义作为解释

  第二种典型的解释是隐藏的神经元或层的意义。与神经科学中的“祖母细胞假说”类似，它是由一种将抽象概念与某些隐藏神经元的激活联系起来的愿望驱动的。以动物分类为例，一些神经元可能对动物的头部有较高的反应，而另一些神经元可能会寻找动物的身体、脚或其他部位。这种定义上的解释提供了全局的可解释性。

1. 被动的，隐藏的语义作为解释，全局:
   现有的隐语义解释方法主要集中在计算机视觉领域。最直接的方法是显示神经元在“寻找”什么，即可视化。可视化的关键是找到一个具有代表性的输入，使某个神经元、通道或层的激活最大化，这通常被称为激活最大化。这是一个优化问题，其搜索空间是潜在的巨大输入(样本)空间。假设我们有一个网络，将一个28×28像素的黑白图像作为输入(如MNIST手写数字数据集)，将有228×28可能的输入图像，尽管它们中的大多数可能是无意义的。在实践中，虽然我们可以找到一个最大激活输入图像与优化，它可能是不现实的和不可解释的。这种情况可以通过一些正则化技术或先验得到帮助。
     我们现在概述一下这些技术。激活最大化框架由Erhan等人引入(尽管它被用于深度信念网络等无监督深度模型)。一般来说，它可以写成
   
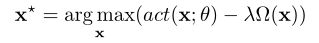
   其中act(·)是激活神经元，θ为网络参数(权重和偏差)，Ω为可选正则化器。
     Simonyan等人首次将激活最大化应用于有监督的深度卷积网络(用于ImageNet分类)。它通过最大化一个类(在softmax之前)的得分来寻找代表性图像。Ω是映射的L2正则化。后来，人们意识到高频噪声是一个主要的麻烦，使图像识别无法完成。为了得到自然和有用的图像识别，找到好的先验或正则化器Ω成为这类方法的核心任务。
     Mahendran和V edaldi提出了一种正则化的总变差
   
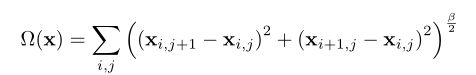
     鼓励相邻像素有相似的值。这也可以看作是一个低通滤波器，可以减少图像中的高频噪声。这种方法通常称为图像模糊。Y osinski等人除了对高振幅和高频信息进行抑制(分别采用l2衰减和高斯模糊)外，还对小值或对激活不重要的像素进行剪切。Nguyen等人建议使用生成模型学习的自然图像先验，而不是使用许多手工制作的正则化器(图像先验)。由于生成对抗网络(Generative Adversarial Networks, GANs)最近在生成高分辨率的真实图像方面表现出了巨大的能力，使用生成对抗网络模型似乎是一个不错的选择。为了得到一个好的总结和许多令人印象深刻的可视化效果，我们建议读者参考[66]。
     除了可视化之外，还有一些工作试图找到内核和视觉概念之间的联系(例如，材料，特定的物体)。Bau 等人收集新的数据集提供的政党pixel-wise二进制面具Lc每个概念c (x),每个输入图像x。激活内核k是高档和地图(给定阈值)转换成一个二进制掩模可(x) x的大小相同。然后内核之间的对齐c k和一定的概念(如汽车)计算
   
   其中|·|是集合的基数，是包含概念c的所有输入x的求和值。沿着同样的思路，Fong和V edaldi 通过用几个核的组合构造M来研究概念在多个核上的嵌入。他们的实验表明，通常需要多个核来编码一个概念，核嵌入可以更好地表示概念。
     Dalvi等人也分析了NLP任务中网络中单个单位/神经元的意义。他们在网络的隐藏神经元和输出之间建立了一个线性模型。然后根据线性模型权重的显著性对神经元进行排序。对于那些排名靠前的神经元，他们的语言意义被研究通过可视化他们输入的显著图，或通过找到他们被激活的最重要的词。

C 被动，归因为解释

  归因是指根据输入特性对输出(预测)的影响，对输入特性给予信任或指责。解释将是一个实值向量，它用分数的符号和振幅表示特征的重要性。对于具有有意义的特征的简单模型(例如线性模型)，我们可以为每个特征全局分配一个分数。当涉及到更复杂的网络和输入时，例如图像，很难说某个像素总是对输出有类似的贡献。因此，许多方法都是在局部进行归因。我们将在下面介绍它们，并在这一节的最后提到一种基于中间表示而不是原始输入特征的全局归因方法。
2. 被动的，归因解释，(半)局部的:
  类似于规则提取方法的分解与教学划分，归因方法也可以分为两组:梯度相关方法和模型不可知方法。
  a)梯度相关和反向传播方法:使用梯度来解释个体分类决策是一种自然的想法，因为梯度代表了损失函数上增长最快的“方向”和速度。梯度也可以根据一个特定的输出类来计算，例如，沿着这个“方向”，一个扰动将使一个输入更可能/更不可能被预测为一只猫/狗。Baehrens等用它来解释高斯过程分类(GPC)、k-NN和SVM的预测。在特殊情况下，线性模型(或一般相加模型)中的特征系数已经是偏导数，换句话说，就是(全局)属性。这样人们就可以直接知道这些特征是如何影响预测的，这也是为什么线性模型通常被认为是可解释的一个重要原因。虽然普通梯度、离散梯度和路径集成梯度已用于属性，但其他一些方法并不使用链式规则计算实际梯度，而只是反向传播属性信号(例如，在反向传播时对每一层进行额外的归一化)。现在我们详细介绍这些方法。
  设f: Rd→{+1，−1}为待解释的(二分类)模型。由于原始输入x∈rd可能是不可解释的(例如，图像中所有像素的张量，或词嵌入[103])，LIME引入了一个中间表示x0∈{0,1}d0(例如:即存在一定的图像补丁或文字)。x0可以恢复到原始输入空间Rd。对于给定的x, LIME[17]试图找到一个潜在的可解释模型g(如线性模型或决策树)作为局部解释。

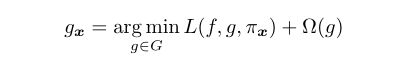
其中G是解释模型族，L是度量f和G之间保真度的损失函数。L是在x0周围的一组扰动样本(及其恢复的输入)上求值，由局部核πx加权。Ω是g的复杂度惩罚，确保g是可解释的。MAPLE 是一种类似的方法，使用局部线性模型作为解释。不同之处在于它将局部定义为数据点在代理随机森林(适合训练过的网络)中落在同一个叶子节点上的频率。
  在计算机视觉中，属性通常表示为显著性映射，即与输入图像大小相同的掩码。在参考[40]中，显著性映射是由梯度生成的(特别是，所有通道的偏导数的最大绝对值)。这种显著性映射不需要任何努力就可以获得，因为它们只需要一次反向传播通道。他们还表明，该方法与之前提出的反卷积网方法等价，只是在ReLU层梯度的计算上有所不同。引导反向传播结合了上述两种方法。它只考虑了在ReLU层反向传播时具有正误差信号的梯度(前者方法)(后者方法)。还有一种变体的Guided Grad-CAM (Gradient-weighted Class Activation Mapping)，它首先在最后一个卷积层计算出一个粗粒度的属性映射(针对某个类)，然后将其与Guided backpropagation得到的属性映射相乘。(Guided GradCAM是CAM的扩展，需要特殊的全局平均池化层。)
  然而，梯度本身可能会产生误导。考虑一个分段连续函数，

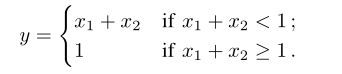
当x1+x2≥1时是饱和的。在x1+x2> 1处，它们的梯度总是0。DeepLIFT指出了这一问题，并强调了除了需要解释的目标输入外，还有参考输入的重要性。参考输入是一种默认的或“中性”的输入，在不同的任务中会有所不同(例如，空白图像或零向量)。实际上，正如Sundararajan等人所指出的，DeepLIFT试图计算的是“离散梯度”，而不是(瞬时)梯度。另一种类似的“离散梯度”方法是LRP(选择一个零向量作为参考点)，不同的是如何计算离散梯度。文献[105]中也提出了这种观点，即LRP和DeepLIFT本质上是计算修正梯度函数的反向传播。
  然而，离散梯度也有其缺点。由于链式法则对离散梯度不成立，deeplifand LRP采用了改进的反向传播形式。这使得它们的属性取决于网络的实现，换句话说，即使是两个功能等价的网络，其属性也可能是不同的(具体例子见参考文献[83]附录B)。综合梯度已经被提出来解决这个问题。定义为输入x与参考输入xref之间直线上所有梯度的路径积分。积分梯度(IG)的第i维定义为:

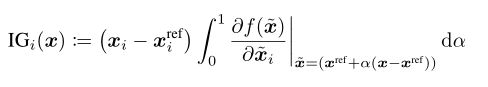
其中是f(x)的梯度的第i维。
  对于需要参考点的归因方法，用户可以根据需要解释的内容选择不同的参考点，从而提供了半局部可解释性。表四总结了上述梯度相关归因方法(改编自[105])。除了前面讨论的“梯度”归因之外，Wang等指出偏差术语可以包含与梯度互补的归因信息。他们提出了一种递归地将偏差归因分配回输入向量的方法。

  这些离散梯度方法(如LRP和DeepLIFT)提供了半局部解释，因为它们解释了目标输入w.r.t.另一个参考输入。但对于解vnet和Guided Backprop等仅用于解释单个输入的方法，由于过程中的整流操作，可以说具有一定的非局部性。此外，人们可以积累多种局部解释，从而具有一定的全局可解释性。例如，SpRAy对个体归因进行聚类，然后总结出一些组预测策略。MAME是另一个类似的方法，它可以生成多级(从局部到全局)解释树。
  虽然我们有许多方法来产生看似合理的显著性图，但显著性图和真实的解释之间仍然有一个小的差距。甚至有一些关于归因方法的对抗例子，这种方法可以产生感知上无法区分的输入，导致相同的预测标签，但非常不同的归因图。研究人员提出了几个特性显著图应该是一个有效的解释。Sundararajan等人(综合梯度法)引入了两个要求，灵敏度和实现不变性。灵敏度要求主要是由于(局部)梯度饱和问题(导致零梯度/属性)。实现不变性意味着两个功能等价的网络(由于DNNs的过度参数化设置，它们可以有不同的学习参数)应该具有相同的属性。Kindermans等人引入了输入不变性。它需要归因方法来反映模型对于输入转换的不变性。例如，带有偏差项的模型可以很容易地处理输入(像素值)的恒定移位。显然，(普通的)梯度归因方法满足这种输入不变性。对于离散梯度和其他使用参考点的方法，它们依赖于参考点的选择。Adebayo等人采取了不同的方法。他们发现，边缘检测器也可以产生与显著性遮罩相似的遮罩，并突出输入的某些特征。但是边缘检测器与网络或训练数据没有任何关系。因此，他们提出了两个测试来验证归因方法是否会失败(1)如果网络的权值被随机噪声替换，或者(2)如果训练数据的标签被打乱。归因方法应该失败，否则它表明该方法不能反映训练过的网络或训练数据(换句话说，它只是一种边缘检测器)。
  b)模型不可知论归因:在博弈论中，有一个任务是“公平”地从所有玩家联盟所产生的总收益中分配给每个玩家收益。形式上设N为N人的集合，v: 2N→R为特征函数，可解释为联盟总收益N。显然，v(∅)= 0。联盟博弈可以用元组hN, vi表示。对于联盟博弈，Shapley值是收益分配问题的解。玩家i的收益(归因)可以如下计算:

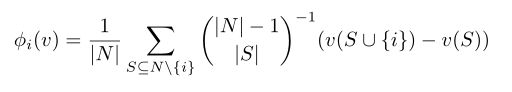
其中为参与人i对联盟s的边际贡献，公式的其余部分可以视为归一化因子。Shapley值的另一种著名形式是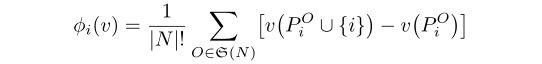
其中σ(N)是一组有序排列的N,和Po,i为球员在N前辈的球员我排列o .ˇStrumbelj v和Kononenko采用这种形式,这样可以在多项式时间近似(参见[72]和[74])。回到(用f表示的)神经网络,让N的所有输入特性(属性),S是一个任意感兴趣的特征子集(S⊆N)。对于一个输入x,特征函数v (S)的区别是预期的模型输出年代,当我们知道所有的特性和预期的输出在没有特征值是已知的(即预期的输出在所有可能的输入),用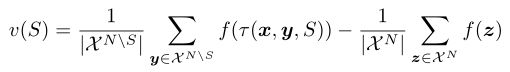
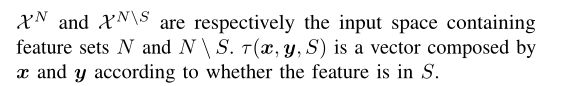
  然而，一个实际问题是指数计算复杂度，更不用说每个v(S)调用的前馈计算成本了。ˇStrumbelj和Kononenko从S(N)×X(笛卡尔积)中采样近似Shapley值。还有其他的变体，如使用不同的v。参考文献[73]提出了统一的观点，不仅包括Shapley值方法，还包括LRP和deelift。通过因果图的镜头也有Shapley值。
  敏感性分析也可以用来评估一个特征的重要性。具体地说，一个特征的重要性可以通过模型输出在一个特征(或多个特征)变化时的变化程度来衡量。有不同种类的变化，例如，扰动，遮挡等。
  Chen等人提出了实例化的特征选择器E，它将输入x映射到条件分布P(S | x)，其中S是原始特征集的任意子集(一定大小)。所选择的特征可以用xS表示。然后，它们的目标是最大化所选特征与输出变量Y之间的互信息，

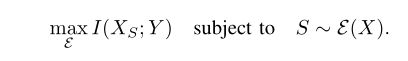
用变分逼近法得到上述问题的易于处理的解。
  根据所问的具体问题，可以用不同的方式计算归因。通常，我们会问这些特征是如何用于预测类c的。然而，Goyal等人试图找到输入图像上的最小编辑，这可能导致不同的预测类c0。换句话说，它们回答了这样一个问题:“输入图像中的哪个区域使得预测是c类，而不是c0类”。
3. 被动的，归因解释，全局的:
  归因并不一定是将“功劳”或“过失”归咎于原始输入或功能。Kim等人提出了一种可以计算任何用户感兴趣的概念的模型灵敏度的方法TCA V(概念激活V器定量测试)。通过首先收集一些带有或不带有目标概念的例子(例如，动物身上的条纹)，这个概念可以用超平面的法向量来表示，将这些正面/负面的例子(带有/不带有条纹的动物图片)放在一个隐藏层中。如果(输入x的)隐含层表示沿着概念向量移动了一个无极小的步骤，那么概念的得分可以计算为(平均)输出灵敏度。这是一种全局可解释性方法，因为它解释了一个概念通常如何影响输出。这些概念除了由人工挑选外，还可以通过对输入段进行聚类自动发现。

D 被动语态，举例说明

  我们回顾的最后一种解释是例子解释。当被要求解释一个新输入时，这些方法会返回支持或反例的其他示例。一个基本的直觉是找到模型认为最相似的例子(就潜在表示而言)。这是局部可解释性，但我们也可以在一个类或更多类中寻找一组具有代表性的样本来提供全局可解释性。提出了一种一般的方法。还有其他方法，例如测量训练示例对目标输入的模型预测的影响程度。这里我们只关注与深度神经网络相关的工作。

1. 被动的、实例解释的、局部的:Koh和Liang提供了一种有趣的方法来评估训练实例对未见测试实例的模型预测的影响程度。首先用近似法计算模型参数随训练实例变化的变化。此外，它对测试点损失的影响可以计算出来。通过检查最有影响力的(积极的或消极的)训练示例(对于测试示例)，我们可以对模型预测有一些见解。Yeh等人表明，logit (softmax之前的神经元)可以分解为训练点在pre-logit层激活的线性组合。训练点的系数表明这些点的相似性是兴奋性的还是抑制性的。以上两种方法都提供了局部的解释。

IV 在培训期间进行积极的解释性干预

  除了从训练好的网络中被动地寻找人类可理解的模式外，研究者还试图在网络训练过程中施加可解释性限制，即我们分类法中的主动解释方法。一个流行的想法是在 损失函数中添加一个特殊的正则化术语Ω(θ) ，也被称为“可解释性损失”(θ收集网络的所有权值)。我们现在根据相关文献所提供的解释形式来讨论。

A 主动的，规则作为解释(半局部或全局)

  Wu等人[87]提出了树正则化方法，它适用于可以被浅层决策树很好地近似的模型。它需要两个步骤:(1)使用数据点x(i)，ˆy(i)来训练二叉决策树;N，其中ˆy = fθ(x)是网络预测，而不是真实标签，(2)计算该决策树在所有数据点上的平均路径长度(从根到叶节点)。然而，树正则化项Ω(θ)是不可微的。为此，引入了代理正则化项ˆΩ(θ)。给定一个数据集?θ(j),Ω(θ(j)) ?J J =1，ˆΩ可以训练为一个多层感知器网络，使平方误差损失最小化

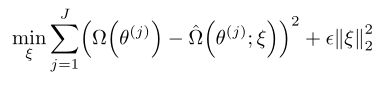
可以在训练网络的同时进行。此外，数据增强技术可以用于产生θ，特别是在早期训练阶段。树正则化使网络易于通过决策树近似，从而实现全局可解释性。后来，作者还提出了区域树正则化，用半局部的方式实现这一点。

B 主动的，隐藏的语义作为解释(全局)

  另一种方法旨在使卷积神经网络更好地学习(解缠)隐藏语义。cnn在看过上述特征可视化技术和一些实证研究后，认为已经学习到了层次结构中的一些低级到高级的表示。但即使高层已经学习了一些对象级别的概念(例如，头、脚)，这些概念通常也会相互纠缠在一起。换句话说，一个高层过滤器可能包含不同图案的混合。Zhang等人提出了一个损耗项，鼓励高层滤波器代表一个单一的概念。具体来说，对于CNN，一个feature map (ReLU后的高层滤波器输出)是一个n × n矩阵。Zhang等人预先定义了一组n2ideal feature map模板(activation patterns) T，每个模板都像一个高斯核，只是其峰值的位置不同。在正向传播过程中，将特征映射按照原始特征映射中最活跃的“像素”的位置，由某个模板T∈T对其进行掩码(元素积)。在反向传播过程中，插入一个额外的损耗，即M(对所有图像计算的滤波器特征映射)和T∪{T−}(所有的理想激活模式加上一个充满负常数的负模式)之间的互信息。这个损失术语使过滤器要么具有一致的激活模式，要么保持不激活。实验表明，它们设计的过滤器在语义上更有意义(例如，过滤器的“接收场对应动物的头部)。

D 主动，归因为解释

  与帮助实现更好的全局可解释性的树正则化(决策树)类似，ExpO 增加了可解释性正则化，以提高局部属性的质量。这种正规化要求模型具有高保真度和稳定的局部属性。DAPr (deep attribution prior)考虑了额外的信息(例如，关于特征重要性的粗略先验)。先验与主预测模型(作为正则化器)一起训练，使模型具有与先验相似的归因。

  除了对个体输入(局部在输入空间中)进行归因外，Dual-net还提出了基于种群的特征重要性确定方法，即为一个输入种群集体找到一个最优特征子集。该方法采用选择器网络生成最优特征子集，操作器网络根据最优特征集进行预测，两种网络共同训练。训练后，选择器网络可用于特征重要性排序。

D 主动的，原型解释(全局)

  Li等人将原型层合并到网络(具体地说，是一个自动编码器)。该网络就像一个原型分类器，根据(编码的)输入和学习原型之间的接近程度做出预测。除了交叉熵损失和(自动编码器)重构误差之外，它们还包括两个可解释性正则化术语，鼓励每个原型至少与一个已编码输入相似，反之亦然。网络经过训练后，这些原型可以很自然地用作解释。Chen等人将原型层添加到常规CNN而不是自动编码器。这个原型层包含原型，这些原型被鼓励模仿输入的部分。当需要解释时，网络可以为输入图像的不同部分分别提供多个原型。

V 评估可解释性

  一般来说，很难客观地评估可解释性，因为最终任务可能非常不同，可能需要来自专家的领域知识。Doshi-V elez和Kim提出了三种评估方法:基于应用的、基于人的和基于功能的。第一个是衡量可解释性对最终任务的帮助程度(例如，更好地识别错误或减少歧视)。以人为基础的方法是，例如，直接让人们通过以人为对象的实验来评估解释的质量(例如，让用户在多种解释中选择质量最高的解释)。基于功能的方法寻找解释质量的代理(例如，稀疏性)。最后一种方法不需要昂贵的人体实验，但如何正确地确定代理是一个挑战。

  在我们的分类法中，解释分为不同的类型。虽然不同类型的解释之间的可解释性很难进行比较，但为此提出了一些衡量标准。对于逻辑规则和决策树，提取的规则模型的大小经常被用作标准(例如规则的数量，每条规则的前因数，决策树的深度等)。严格地说，这些标准更多地衡量的是解释是否可以有效地解释。隐语义方法对网络中的某些隐单元进行解释。网络解剖通过计算隐藏单元与特定概念的匹配度来量化其可解释性。至于隐藏的单位可视化方法，目前还没有一个好的测量方法。对于归因方法，他们的解释是显著图/掩码(或根据具体任务的特征重要性等)。Samek等人通过性能退化来评估显著性映射，如果输入图像按从显著到不显著斑块的顺序被噪声部分掩盖。和Hooker等人提出了一种类似的评估方法。建议使用固定的无信息值而不是噪声作为掩码，并在再训练模型上评估性能退化。Samek等人也将熵作为另一种度量方法，他们认为，好的显著性地图关注的是相关区域，不包含太多的无关信息和噪声。Montavon等人希望解释函数(将输入映射到显著性映射)是连续的/平滑的，这意味着当看到相似的输入时解释(显著性映射)不应该变化太多。

VI 应用

  在实践中，不同的解释方法各有优缺点。被动网络(post-hoc)方法由于其直接性和可应用于大多数现有网络而得到了广泛的研究。人们可以选择利用网络内部信息的方法(如连接权值、梯度)，这些方法通常更有效(如见第三- c1a段)。除此之外，还有一些与模型无关的方法，这些方法不需要模型架构，它们通常计算某个输入特征的边际效应。但是这种通用性也是被动方法的缺点，特别是因为没有简单的方法可以与其他领域知识/先验结合。主动(可解释性干预)方法有一些关于网络应该如何优化的想法。这个网络可以被优化到很容易被决策树适应，或者有更适合目标任务的首选特征属性。(再次强调，这种主动干预的另一面是需要网络和解释方法之间的兼容性。)

  至于第二个维度，解释的格式，逻辑规则是最清楚的(不需要进一步的人为解释)。然而，它应该控制解释的复杂性(例如，决策树的深度)，否则解释在实践中不会有用。隐藏语义本质上解释了网络的一部分，大部分工作集中在计算机视觉领域。归因非常适合解释个体的输入。但通常很难从归因(与逻辑规则相比)得到对网络的总体理解。举例解释的解释力是最低的(最隐含的)，并且不会获得很多研究兴趣。

  对于最后一个维度，当我们更关心每一个单独的预测(例如，信用或保险风险评估)时，局部解释更有用。对于一些科学研究领域，如基因组学和天文学，全局解释更受欢迎，因为它们可能揭示一些普遍的“知识”。请记住，在局部和全局可解释性之间并没有明确的界限。在一些解释融合方法(例如MAME)的帮助下，人们可以从多级(从局部到全局)解释中受益。

VII 结论

  在这个综述中，我们提供了一个全面的审查神经网络的可解释性。首先，我们讨论了可解释性的定义，并强调了解释格式和领域知识/表示的重要性。具体来说，有四种常见的解释类型:逻辑规则、隐含语义、归因和实例解释。然后，通过回顾以往的文献，我们总结了可解释性之所以重要的3个基本原因:高可靠性系统的要求、伦理/法律要求和科学的知识发现。之后，我们对现有的网络解释方法进行了新的分类。它沿着三个维度演化:被动与主动、解释类型和全局与局部解释。最后两个维度不是纯粹的范畴，而是有序数值(例如，半局部)。这是我们第一次对可解释性研究有一个连贯的概述，而不是许多孤立的问题和方法。我们甚至可以根据我们的分类在3D空间中可视化现有方法的分布。

  从新分类法的角度来看，可解释性研究仍有几个可能的研究方向。首先，主动解释性干预方法尚未得到充分的探讨。对被动方法的一些分析也表明，神经网络不一定要学习人类容易解释的表示。因此，如何在不损害网络性能的情况下主动地使网络具有可解释性仍然是一个有待解决的问题。在调查过程中，我们看到了越来越多的最近的工作填补了这一空白。

  另一个重要的研究方向可能是如何更好地将领域知识整合到网络中。正如我们在本文中看到的，可解释性就是提供解释。解释建立在可理解的术语(或概念)之上，这些术语或概念可能是特定于目标任务的。我们已经有很多方法构造解释不同类型的,但使用的与领域相关的条款的解释仍非常简单(见表1)。如果我们可以利用更多的域/任务相关的术语,我们可以获得更多信息的解释和更好的可解释性。