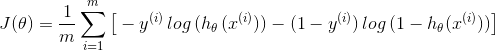数据分析与机器学习学习笔记--线性回归与逻辑回归
1.引言
线性回归与逻辑回归,作为初识机器学习的两个经典算法拥有大量的实践经验,这两个算法的名称虽然都包含回归,但其内容并非如此,其中线性回归的作用是对连续性数据进行回归分析,而逻辑回归确实一个作用于离散型数据的经典分类算法。正如我上篇文章所说的没有最好的算法只有最合适的算法,在kaggle竞赛排行榜中这两个算法总体表现是最好的,虽然没有夺得过最好的排名,但是总体精度确非常优秀,也就是比较中庸,因为这两个算法比较简单,所以面对一个问题时优先考虑线性回归和逻辑回归,如果不合适再更换算法。
2.线性回归(Linear Regression)
线性回归是最为经典的回归选法,此处将算法共分为以下三个部分,设置损失函数和代价函数,设置目标函数,优化求解目标函数对线性回归进行推理。
2.1 损失函数(lost)、代价函数(cost)和目标函数(obj)
2.2 优化求解过程
损失函数和代价函数额设置:上式1、2分别为我们设置的lost function和cost function,我们选取预测值与真实值差值的平方作为我们的lost,同样的我们的cost如上篇所介绍的进行求和并除以1/2m进行求总体的平均值,此处取1/2m的作用是在下一步进行剃度下降更新参数时我们需要求导,对cost求导后2次方会将之前的1/2约掉,使整体式子更加简洁。
目标函数的设置:3式即为添加了L2正则化惩罚项的obj function,正则化项前面的参数的作用是决定我们的惩罚力度,也即我们的正则化力度。
优化求解目标函数:此部分的分部过程我放在最后的梯度下降中进行详细推理。
3.逻辑回归(Logistic Regression)
逻辑回归是最为经典的二分类问题,此处将算法共分为以下四部分,设置损失函数和代价函数,通过sigmod函数转化,设置目标函数,优化求解目标函数对逻辑回归进行推理。
3.1 损失函数(lost)、代价函数(cost)和目标函数(obj)
3.2 优化求解过程
损失函数和代价函数的设置:上式1、2分别为逻辑回归的lost function和cost function,在研究逻辑回归的损失函数如何设置时出现了问题,当时最初的想法是沿用线性回归的损失函数,但是在操作过程中发现并不合适,此难题一度搁置,经过一段时间的研究,大佬们提出了如下的损失函数(懒得一步一步打公式了直接截了个图,见谅见谅,什么都没看到),由于使用此式子计算起来十分复杂,于是乎我们在此进行求对数似然函数就得到了上部1、2的式子,其中y(预测值)的取值为0或1,当y=0时其概率取决于后一部分,当y=1时我们的结果取决于前一部分。
sigmoid函数:上式中的![]() 为计算结果为1的概率,其原因在之后模块的sigmoid函数进行了讲解。
为计算结果为1的概率,其原因在之后模块的sigmoid函数进行了讲解。
目标函数的设置:对1、2式子进一步简化表示,我们将各参数通过矩阵形式表示,由此得出了4式,让后我们依旧进行添加L2正则化惩罚项防止过拟合(老规矩不用多说)。
优化求解目标函数:此部分计算过程与线性回归类似,在之后的部分我没有进行详细推导。
4.sigmoid函数
sigmoid函数的图形为一条优美的S形曲线(女生们梦寐以求的身材),该函数将输入数值转换为[0, 1]之间的概率输出,由此将根据参数优化后的到的theta值计算出的结果输入到sigmod函数中计算出概率,当样例的输出的概率大于0.5时将该样例归入标签1类,当其输出概率小于0.5时将其归入便签0类,sigmoid函数在机器学习领域具有重要地位。
5.梯度下降
剃度下降是求解优化目标函数的常用方法,当然梯度下降不是唯一方法,还有牛顿法,拟牛顿法等等,剃度下降通俗来说就是在每一点计算函数在各方向的偏导数,求出下降最快的方向,而剃度在高数中的含义就是函数下降最快的方向。举一个最为简单且容易理解的同时也是各种机器学习中最常见的例子,假设我们站在一座山的最高峰,而我们的目标就是走到该山的最低点,由此我们站在山顶发现一个方向下降最快,我们朝着这个放向走了一小步,此时我们的位置更新但是还没有到达最低点,在此位置上我们再此寻找方向下降最快的方向,再次走一小步......依此类推,直到找到最小点。
以下为三种梯度下降策略,三种方式各有优点同时也有不足,不过我们通常使用的是第三种,即小批量梯度下降。再次处我仅将线性回归的求解过程详细给出,逻辑回归的求解过程类似(在这里我深刻感觉到咱们老祖宗的大智慧,中庸,这个中庸可忒牛xx了,如同我们今天介绍的算法一样,没有特别突出的时刻,但是在每一个数据集上表现都不差,差不多差不多着到最后总体结果就异常优秀了!!!!)
5.1 完全(批量)剃度下降
如何求解梯度下降,上文已知我们需要对代价函数求导(多参数情况下进行求偏导),如第一个式子,我们对代价函数求theta的偏导,因为在之前设置cost函数时将之前的参数设置为1/2m,再次求导后将1/2约掉,得到上式,此部分即为我们所求的更新部分也就是下山的方向;第二个式子即是我们更新的函数也即下山走的那一小步,下降的大小还与我们设置的参数有关。
完全(批量)剃度下降此方法考虑的是所有参数以及大量样本,容易得到最优的解,但是正如所说,需要考虑大量的样本,所以迭代计算的过程会很慢,在实际训练过程中数据量过于庞大不推荐此种方法。
5.2 随机梯度下降
此部分求解剃度下降的过程与完全梯度下降一致,但是随机梯度下降仅随机选择一个参数进行迭代,但是不容易得到最优解,正与完全剃度下降相反,此种方法迭代计算的过程非常快,但是由于仅仅考虑一个方向,有可能会适得其反,并不会造成下降反而上升,同样不推荐此种方法。
5.3 小批量梯度下降
好的,下面该是我们的“猪脚”闪亮登场了,小批量剃度下降,正如其名字,我们在迭代的时候随机选择一部分样本进行迭代,此方法结合了以上两种方法的优势,在实践过程中发现其有时会产生优于完全剃度下降的结果,在实际训练过程推荐此方法。
6.总结
本此写的线性回归和逻辑回归比较仓促,比计划中要费的时间多一些,在大量博客中线性回归与逻辑回归是分为两章进行编写,但是在此我考虑到二者名字比较相近,都包含回归二字(切记不要被名字迷惑,眼见不一定为实,就如我的名字,看起来里面有个正字,但是我本身也非常非常正直),所以我将两个算法放在一起做一个比较记忆。
(PS:本篇大部分公式还是自己写的,但是鄙人还是不要脸的在别人博客中截了几个图片大家不要打我)
(8302四朵金花天团强势出境)