python数据分析-NumPy学习

一、 数据分析环境搭建

1. anaconda环境搭建

Conda 是一个开源的软件包管理系统和环境管理系统，用于安装多个版本的软件包及其依赖关系，并在它们之间轻松切换。Conda 是为 Python 程序创建的，适用于 Linux，OS X 和Windows，也可以打包和分发其他软件 。最流行的 Python 环境管理工具。

conda官网上下载安装，安装过程不停下一步就行。打开conda,调用里面的jupyter功能。
可以实现在线编写python，并进行可视化分析。

2.pycharm中调用anaconda中的库

安装好conda之后，之前使用PYcharm 去 pip install matpllotlip的包时候，始终出现错误，方法的根本出发点在于，Pycharm本身缺少numpy和matplotlib这些库，而另一个Python的开发环境Anaconda则自带了300多种常见的库。所以想在pycharm中使用Anaconda自带的库。实现这一“借用”的则是Pycharm中对 “Project Interpreter”的设置，该设置是设定Pychar使用哪一个python编译器。那么只要将该interpreter设置为Anaconda下的python.exe，就可以将Anaconda下众多的库导入到Pycharm中。（这是一种借用conda的方法，但让pycharm自己去调用库的问题始终没有解决）

用pycharm调用conda的库并使用

3.建议的学习顺序

NumPy是使用Python进行科学计算的基础包，常用于数据分析。NumPy通常与SciPy和Matplotlib一起使用，广泛用于替代matlab，有助于我们学习数据科学或机器学习。
Matplotlib是用于数据可视化的最流行的Python包之一，它是一个跨平台库，用于根据数组中的数据制作2D和简单3D图。
Pandas是一款开放源码的BSD许可的Python库，为Python编程语言提供了高性能，易于使用的数据结构和数据分析工具。Pandas用于广泛的领域，包括金融，经济，统计，分析等学术和商业领域。

二、NumPy学习

Numpy的核心：多维数组

1. 代码简洁：减少Python代码中的循环。
2. 底层实现：厚内核©+薄接口(Python)，保证性能。
   学习numpy，参考视频是numpy学习视频
   

1.学习预备概念

a.相对路径和绝对路径

怎么理解补充一下
附上一个链接

b.空值（nan ）和无穷（inf）

c.Numpy副本和视图

## 列表


list01 =[1,2,3,4,5,6]
list02 =list01#两个地址是一样的，都是指向同一个内存地址
print(list01,list02)

print(id(list01))
print(id(list02))

# copy()函数，浅复制

list02=list01.copy()

print(id(list01))
print(id(list02))

## 深复制

#导入模块
import copy

list03 = [1,2,3,[4,5,6]]
print(list03)
list03

list04=copy.deepcopy(list03)
list04

#修改list01第三个元素中的第0个数值
list03[3][0]=100
list03

list04

2.Numpy的数据类型

a.数据类型

numpy 支持的数据类型比 Python 内置的类型要多很多，基本上可以和 C 语言的数据类型对应上，其中部分类型对应为 Python 内置的类型。下表列举了常用 NumPy 基本类型。

名称	描述	字符码
np.bool	用一个字节存储的布尔类型（True或False）	‘b’
np.int8	一个字节大小，-128 至 127 （一个字节）	‘i’
np.int16	整数，-32768 至 32767 （2个字节）	'i2‘
np.int32	整数，（4个字节）	‘i4’
np.int64	整数，（8个字节）	‘i8’
np.uint8	无符号整数，0 至 255	‘u’
np.uint16	无符号整数，0 至 65535	‘u2’
np.uint32	无符号整数	‘u4’
np.uint64	无符号整数	‘u8’
np.float16	半精度浮点数：16位，正负号1位，指数5位，精度10位	‘f2’
np.float32	单精度浮点数：32位，正负号1位，指数8位，精度23位	‘f4’
np.float64	双精度浮点数：64位，正负号1位，指数11位，精度52位	‘f8’
np.complex64	复数，分别用两个32位浮点数表示实部和虚部	‘c8’
np.complex128	复数，分别用两个64位浮点数表示实部和虚部	‘c16’
np.object_	python对象	‘O’
np.string_	字符串	‘S’
np.unicode_	unicode类型	‘U’

3.数组的定义和创建

a. ndarray数组定义

用np.ndarray类的对象表示n维数组

import numpy as np

ary = np.array([1, 2, 3, 4, 5, 6])
print(type(ary),ary)
# [1 2 3 4 5 6]

b. ndarray数组创建

numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)

名称	描述
object	数组或嵌套的数列
dtype	数组元素的数据类型，可选
copy	对象是否需要复制，可选
order	创建数组的样式，C为行方向，F为列方向，A为任意方向（默认）
subok	默认返回一个与基类类型一致的数组
ndmin	指定生成数组的最小维度

import numpy as np # 用np代替numpy,让代码更简洁

a = [1,2,3,4] # 创建列表a
b = np.array([1,2,3,4]) # 从列表a创建数组b，array就是数组的意思
print(a)
print(type(a)) # 打印a的类型

print(b)
print(type(b)) # 打印b的类型

#观察输出值的区别，列表和数组的区别是什么？
#[1, 2, 3, 4]
#
#[1 2 3 4]
#

创建数组的几种方式：

创建一维数组和二维数组

   # 创建一维数组
   c = np.array([5,6,7,8])
   print(c)
   # 创建二维数组
   d = np.array([[1,2],[3,4],[5,6]])
   print(d)
   print(type(d))
   
   #[5 6 7 8]
#[[1 2]
# [3 4]
 #[5 6]]

np.arange

np.arange(起始值(0),终止值,步长(1))

   numpy.arange(start, stop, step, dtype)
   
   # 1个参数:参数值为终止值，起始值取默认值0，步长为1，左闭右开
   x = np.arange(5)
   print(x)
   
   # 2个参数:参数值为起始值，终止值，步长默认为1 ，左闭右开
   y = np.arange(5,10)
   print(y)
   
   # 3个参数:参数值为起始值，终止值，步长为2 ，左闭右开
   z = np.arange(10,20,2)
   print(z)
#[0 1 2 3 4]
#[5 6 7 8 9]
#[10 12 14 16 18]

np.zeros

np.zeros(数组元素个数, dtype=‘类型’)

   numpy.zeros(shape, dtype = float, order = 'C')
   
   e = np.zeros(10)
   print(e)
#[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]

np.ones

np.ones(数组元素个数, dtype=‘类型’)

   numpy.ones(shape, dtype = None, order = 'C')
   
   f = np.ones(10)
   print(f)
#[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

np.random

np.random中的函数来创建随机一维数组

1. np.random.randn()

   创建一个一维数组，其中包含服从标准正态分布（均值为0、标准差为1的分布）的n个随机数

2. np.random.rand()

   生成的一维数组中包含的就是0～1之间的n个随机数

   # 创建一个包含5个随机数的正态分布一维数组
   g = np.random.randn(5)
   print(g)
   
   # 创建一个范围在0~1之间的含有5个随机数的一维数组
   h = np.random.rand(5)
   print(h)
#[ 0.68384377  0.278969    0.31402352 -0.19564941 -0.07348227]
#[0.59140982 0.77833598 0.33633508 0.46787355 0.34251799]

   # 其他函数
   zeros_like， ones_like， empty， empty_like， linspace， numpy.random.Generator.rand， numpy.random.Generator.randn， fromfunction， fromfile，set_printoptions

numpy.empty

numpy.empty方法用来创建一个指定形状（shape）、数据类型（dtype）且未初始化的数组

   numpy.empty(shape, dtype = float, order = 'C')
   
   import numpy as np 
   x = np.empty((3,2), dtype = int) 
   print (x)
#[[ 869667760        589]
# [ 253155624 -618297307]
# [ 869667824        589]]

numpy.linspace

numpy.linspace函数用于创建一个一维数组，数组是一个等差数列构成的

   np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

参数	描述
start	序列的起始值
stop	序列的终止值，如果endpoint为true，该值包含于数列中
num	要生成的等步长的样本数量，默认为50
endpoint	该值为 true 时，数列中包含stop值，反之不包含，默认是True。
retstep	如果为 True 时，生成的数组中会显示间距，反之不显示。
dtype	ndarray 的数据类型

   import numpy as np
   a = np.linspace(1,10,10)
   print(a)
# [ 1.  2.  3.  4.  5.  6.  7.  8.  9. 10.]

创建二维数组

1. 创建一维数组的np.arange()函数和reshape()函数来创建二维数组

      # 创建一个3行4列的二维数组
      i = np.arange(12).reshape(3,4)
      print(i)
#[[ 0  1  2  3]
# [ 4  5  6  7]
 #[ 8  9 10 11]]

2. np.random.randint()函数用于创建随机整数数组

      j = np.random.randint(0,10,(4,4))
      print(j)
      
      # 括号里第1个参数0为起始数，第2个参数10为终止数，第3个参数（4,4）则表示创建一个4行4列的二维数组。
 #[[6 5 7 2]
 #[9 3 8 7]
 #[1 1 4 3]
 #[5 6 6 7]]

从已有的数组创建数组

numpy.asarray 类似 numpy.array，但 numpy.asarray 参数只有三个，比 numpy.array 少两个

numpy.asarray(a, dtype = None, order = None)

参数	描述
a	任意形式的输入参数，可以是列表, 列表的元组, 元组, 元组的元组, 元组的列表，多维数组
dtype	数据类型，可选
order	可选，有"C"和"F"两个选项,分别代表，行优先和列优先，在计算机内存中的存储元素的顺序。

   import numpy as np 
    
   x =  [1,2,3] 
   a = np.asarray(x)  
print (a)
#[1 2 3]

4.数组的属性

• ndarray.shape - 维度，数组的尺寸。这是一个整数元组，指示每个维度中数组的大小。对于具有n行和m列的矩阵(n,m)
• ndarray.dtype - 描述数组中元素类型的对象。
• ndarray.size - 数组元素的总数。等于shape的乘积。
• ndarray.ndim - 数组的轴数（尺寸）。len(shape)(长度)。
• ndarray.itemsize - 数组中每个元素的大小（以字节为单位）。
• ndarray.nbytes - 总字节数 = size x itemsize。
• ndarray.real - 复数数组的实部数组。
• ndarray.imag - 复数数组的虚部数组。
• ndarray.T - 数组对象的转置视图。
• ndarray.flat - 扁平迭代器。

5.数组的维数

数组的轴数（尺寸）

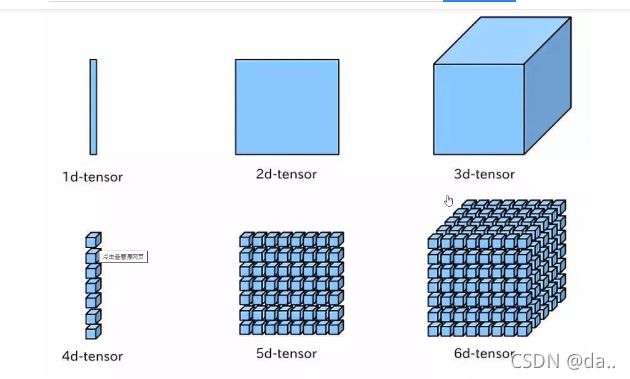
a.什么是轴?

​ 在numpy中可以理解为方向，使用0，1，2数字表示

​ 对于1维数组，只有一个0轴;

​ 对于2维数组（shape（2，2))有0轴和1轴;

​ 对于3维数组（shape（2，2，3））有0，1，2轴;

b.为什么要学习轴?

​ 有了轴的概念后，我们计算会更加方便，比如计算一个2维数组的平均值，必须指定是计算哪个方向上面的数字的平均值。

import numpy as np

a = np.array([[1, 2, 3], [4, 5, 6]])
print(np.sum(a, axis=0))
print(np.sum(a, axis=1))
print(np.sum(a))  # 计算所有的值的和

# 三维的数据
a = np.arange(27).reshape((3, 3, 3))
print(a)

b = np.sum(a, axis=0)
print(b)

c = np.sum(a, axis=2)
print(c)
’‘’’‘’‘’’‘’‘’‘’’‘编译结果如下:
[5 7 9]
[ 6 15]
21
[[[ 0  1  2]
  [ 3  4  5]
  [ 6  7  8]]

 [[ 9 10 11]
  [12 13 14]
  [15 16 17]]

 [[18 19 20]
  [21 22 23]
  [24 25 26]]]
[[27 30 33]
 [36 39 42]
 [45 48 51]]
[[ 3 12 21]
 [30 39 48]
 [57 66 75]]

总结： 在计算的时候可以想象成是每一个坐标轴，分别计算这个轴上面的每一个刻度上的值，或者在二维数组中记住0表示行1表示行列。

import numpy as np

ary = np.array([
    [1,2,3,4],
    [5,6,7,8]
])
print(ary.ndim)
#2

c.数组维度有关的属性

ndarray.shape

数组的维度。这是一个整数元组，指示每个维度中数组的大小。对于具有n行和m列的矩阵，shape将为(n,m)。shape因此，元组的长度 是轴数ndim。

import numpy as np

ary = np.array([1, 2, 3, 4, 5, 6])
print(type(ary), ary, ary.shape,ary.dtype)

#二维数组
ary = np.array([
    [1,2,3,4],
    [5,6,7,8]
])
print(type(ary), ary, ary.shape)
# [1 2 3 4 5 6] (6,) int32
# [[1 2 3 4],[5 6 7 8]] (2, 4)

ndarray.size

数组元素的个数。这等于的shape的乘积。

import numpy as np

ary = np.array([
    [1,2,3,4],
    [5,6,7,8]
])

# 观察shape，size，len的区别
print(ary.shape, ary.size, len(ary))
(2, 4) 8 2

ndarray.dtype

描述数组中元素类型的对象。可以使用标准Python类型创建或指定dtype。另外，NumPy提供了自己的类型。numpy.int32，numpy.int16和numpy.float64是一些示例。

import numpy as np

ary = np.array([1, 2, 3, 4, 5, 6])
print(type(ary), ary, ary.dtype)

#转换ary元素的类型
b = ary.astype(float)
print(type(b), b, b.dtype)

#转换ary元素的类型
c = ary.astype(str)
print(type(c), c, c.dtype)

ndarray.itemsize

数组中每个元素的大小（以字节为单位）。例如，类型为元素的数组float64具有itemsize8（= 64/8），而类型complex32中的一个具有itemsize4（= 32/8）。等同于ndarray.dtype.itemsize。

import numpy as np

a = np.arange(15).reshape(3, 5)
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])
       
a.itemsize

d.自定义复合类型

# 自定义复合类型
import numpy as np

data=[
	('zs', [90, 80, 85], 15),
	('ls', [92, 81, 83], 16),
	('ww', [95, 85, 95], 15)
]

#第一种设置dtype的方式
a = np.array(data, dtype='U3, 3int32, int32')
print(a)
print(a[0]['f0'], ":", a[0]['f1'])
print("=====================================")

#第二种设置dtype的方式
b = np.array(data, dtype=[('name', 'str_', 2),
                    ('scores', 'int32', 3),
                    ('age', 'int32', 1)])
print(b[0]['name'], ":", b[0]['scores'])
print("=====================================")

#第三种设置dtype的方式
c = np.array(data, dtype={'names': ['name', 'scores', 'ages'],
                    'formats': ['U3', '3int32', 'int32']})
print(c[0]['name'], ":", c[0]['scores'], ":", c.itemsize)
zs : [90 80 85] : 15 28  # 元素字节数
print("=====================================")

#第四种设置dtype的方式  
d = np.array(data, dtype={'name': ('U3', 0),
                    'scores': ('3int32', 16),
                    'age': ('int32', 28)})
print(d[0]['names'], d[0]['scores'], d.itemsize)

print("=====================================")

#测试日期类型数组
f = np.array(['2011', '2012-01-01', '2013-01-01 01:01:01','2011-02-01'])
['2011' '2012-01-01' '2013-01-01 01:01:01' '2011-01-01']

f = f.astype('M8[D]')
['2011-01-01' '2012-01-01' '2013-01-01' '2011-01-01']

f = f.astype('i4')
[14975 15340 15706 14975]

print(f[3]-f[0])
0

f.astype('bool')
array([ True,  True,  True,  True])

6.数组索引和切片

a.索引操作

一般索引：

import numpy as np
array01=np.arange(1,10)
array01[5]#索引
list02=[[1,2,3,4,5],[7,8,9,10,11],[12,34,6,6,8]]
array03=np.array(list02)
array03[0,3]#索引

高级索引：NumPy 比一般的 Python 序列提供更多的索引方式。除了之前看到的用整数和切片的索引外，数组可以由整数数组索引、布尔索引及花式索引。
高级索引-菜鸟笔记

b.一维数组切片操作

数组对象切片的参数设置与列表切片参数类似

步长+：默认切从首到尾

步长-：默认切从尾到首

数组对象[起始位置:终止位置:步长, …]

默认位置步长：1

import numpy as np

a = np.arange(1, 10)
print(a)  
print(a[:3])  
print(a[3:6])   
print(a[6:]) 
print(a[::-1])  
print(a[:-4:-1])  
print(a[-4:-7:-1])  
print(a[-7::-1])  
print(a[::])  
print(a[:])  
print(a[::3])  
print(a[1::3])  
print(a[2::3]) 

c.多维数组的切片操作

数组对象[页号, 行号, 列号]，下标从0开始，到数组len-1结束。

import numpy as np

a = np.arange(1, 28).reshape(3,3,3)
print(a)

#切出1页 
print(a[1, :, :])		

#切出所有页的1行
print(a[:, 1, :])		

#切出0页的1行1列
print(a[0, :, 1])		

练习：

import numpy as np

a = np.arange(10)
print(a[2:7:2])
print(a[2],a)
print(a[2:])

t1 = np.arange(24).reshape(4,6)
print(t1) 
print('*'*20) 
print(t1[1]) 
print(t1[1,:])  
print(t1[1:]) 
print(t1[1:3,:]) 
print(t1[[0,2,3]]) 
print(t1[[0,2,3],:]) 
print(t1[:,1])
print(t1[:,1:]) 
print(t1[:,[0,2,3]]) 
print(t1[2,3])
print(t1[[0,1,1],[0,1,3]])

7.数组的操作

注意： 要结合学习。 我对numpy的笔记大部分只是仅限于框架引领作用，不可能做到面面俱到，所以语法细节大部分要去对比菜鸟笔记以及numpy官网（百度numpy即可，注意使用谷歌浏览器可以即时翻译）结合学习。

a.形状操作

numpy.shape()、numpy.resize()、numpy.flatten()、numpy.reshape(）、numpy.ravel()

**ndarray的形状：**

four = np.array([[1,2,3],[4,5,6]])
# shape修改的是原有的
four.shape = (3,2) 
four

# reshape返回一个新的数组 
four = four.reshape(3,2) 
four

# 将多维变成一维数组 
five = four.reshape((6,),order='F') 
# 默认情况下参数order=‘C’以行为主的顺序展开，‘F’（Fortran风格）意味着以列的顺序展开 

six = four.flatten(order='F') 
five 
six 

# 拓展：数组的形状 
t = np.arange(24) 
t
t.shape

# 转换成二维 
t1 = t.reshape((4,6)) 
t1 
t1.shape

# 转成三维 
t2 = t.reshape((2,3,4)) 
t2
t2.shape


**视图变维（数据共享）：** reshape() 与 ravel() 


import numpy as np
a = np.arange(1, 9)
print(a)		# [1 2 3 4 5 6 7 8]
b = a.reshape(2, 4)	#视图变维  : 变为2行4列的二维数组
print(b)
[[1 2 3 4]
 [5 6 7 8]]

c = b.reshape(2, 2, 2) #视图变维    变为2页2行2列的三维数组
print(c)
[[[1 2]
  [3 4]]

 [[5 6]
  [7 8]]]

d = c.ravel()	#视图变维	变为1维数组
print(d)
[1 2 3 4 5 6 7 8]


**复制变维（数据独立）：**flatten()


e = c.flatten()
print(e)
[1 2 3 4 5 6 7 8]

a += 10
print(a, e, sep='\n')
[11 12 13 14 15 16 17 18]
[1 2 3 4 5 6 7 8]


# 比较
ndarray.shape， reshape， resize， ravel


**就地变维：直接改变原数组对象的维度，不返回新数组**


a.shape = (2, 4)
print(a)
[[11 12 13 14]
 [15 16 17 18]]

a.resize(2, 2, 2)
print(a)
[[[11 12]
  [13 14]]

 [[15 16]
  [17 18]]]

以下代码是看视频写在jupyter notebook上的代码。
import numpy as np

array01=np.arange(32)
array01

array01.shape

array01.ndim

#就地变维:直接改变原数组对象的维度，不返回新数组
array01.shape=(1,32)
array01

array01.shape=(2,16)
array01

array01.shape=(4,8)
array01

array01.shape=(32,1)
array01

array01.shape=(2,4,4)
array01

#就地变维：等同于上面。
array01.resize(2,4,4)
array01

#复制变维:两个内存地址，数据独立
array02=array01.flatten()
array02

print(id(array01))
print(id(array02))

#视图变维（表面上看是一个4行8列的，但是本质上来说，
#他并没改变，只是视图上的变维，本质是没有任何改变）
array02.reshape(4,8)


array02

array03=array02.reshape(4,8)

array03

print(id(array03))
print(id(array02))

#raval()
array03=array02.reshape(4,8)
array03

array03.shape

array03.ndim

np.ravel(array03,order="C")

np.ravel(array03,order="F")

array03

b.数组数值的修改和添加元素

numpy.reshape()

numpy.append()

 #1. numpy.append 

numpy.append(arr, values, axis=None)
 函数在数组的末尾添加值。追加操作会分配整个数组，并把原来的数组复制到新数组中。此外，输入# 数组的维度必须匹配否则将生成ValueError。

‘’’
参数说明：
arr：输入数组
values：要向arr添加的值，需要和arr形状相同（除了要添加的轴）
axis：默认为 None。
当axis无定义时，是横向加成，返回总是为一维数组！
当axis有定义的时候，分别为0和1的时候（列数要相同）。
当axis为1时，数组是加在右边 （行数要相同）。
‘’’

a = np.array([[1,2,3],[4,5,6]])
a
 
#向数组添加元素：
np.append(a, [7,8,9]) 
 

#沿轴 0 添加元素
np.append(a, [[7,8,9]],axis = 0) 
 

#、 沿轴 1 添加元素：
np.append(a, [[5,5,5],[7,8,9]],axis = 1)

numpy.insert()

numpy.insert(arr, obj, values, axis)

# 函数在给定索引之前，沿给定轴在输入数组中插入值。 
# 如果值的类型转换为要插入，则它与输入数组不同。插入没有原地的，函数会返回一个新数组。此外，如果未提供轴，则输入数组会被展开。

a = np.array([[1,2],[3,4],[5,6]])
a

# 未传递 Axis 参数。 在插入之前输入数组会被展开 
np.insert(a,3,[11,12])

# 传递了 Axis 参数。 会广播值数组来配输入数组
# 沿轴0
np.insert(a,1,[11],axis = 0)

# 沿轴1
np.insert(a,1,11,axis = 1)

这段代码是参考上述视频编写的学习代码
import numpy as np

t=np.arange(24).reshape(4,6)
t

#整数的索引和切片
t[1,2]=800
t

t[0:2,0:2]

#整数数组索引
t[[0,1,2],[0,1,3]]=500
t

#布尔索引
t[t>15]=1500
t

#花式索引
t[t>15]=1500
t

#数组数值的修改
t[1,:]=0
t

t[:,1]=0
t

t[1:3,:]=0
t

t[:,1:4]=0
t

t[1:4,2:5]=0
t

t[[0,1],[0,3]]=0
t

#数组添加元素;append()添加
array02=np.arange(24).reshape(4,6)
array02

array03=np.append(array02,25)
array03

print(id(array02))
print(id(array03))

array04=np.arange(6)
array03=np.append(array02,array04)#没有axis就直接拉平
array03

array04=np.arange(6)
array04

array04=np.arange(6).reshape(1,6)
array04

array03=np.append(array02,array04,axis=0)#以行为标准
array03

array04=np.arange(4).reshape(4,1)
array04

array03=np.append(array02,array04,axis=1)#以列为标准
array03

#insert添加

array02

array04=np.arange(4)
array04

array05=np.insert(array02,2,array04,axis=1)
array05

array02

c.删除数组元素

numpy.delete()

# numpy.delete 

numpy.delete(arr, obj, axis)
# 函数返回从输入数组中删除指定子数组的新数组。 与insert()函数的情况一样，如果未提供轴参数，则输入数组将展开。

''' 
参数说明： 
arr：输入数组 
obj：要沿指定轴删除的子数组的索引，接收切片，整数或整数数组
axis：沿着它删除给定子数组的轴，如果未提供，则输入数组会被展开 
'''

a = np.arange(12).reshape(3,4)
a

# 未传递 Axis 参数。 在删除之前输入数组会被展开 
np.delete(a,5)
 
# 删除每一行中的第二列 
np.delete(a,1,axis = 1)

numpy.unique()

# numpy.unique 函数用于去除数组中的重复元素。

numpy.unique(arr, return_index, return_inverse, return_counts)

''' 
参数说明：
arr：输入数组，如果不是一维数组则会展开 
return_index：如果为true，返回新列表元素在旧列表中的位置（下标），并以列表形式储 
return_inverse：如果为true，返回旧列表元素在新列表中的位置（下标），并以列表形式储 
return_counts：如果为true，返回去重数组中的元素在原数组中的出现次数 
'''

a = np.array([5,2,6,2,7,5,6,8,2,9])
a

# 第一个数组的去重值
u = np.unique(a) 
u

# 去重数组的索引数组
u,indices = np.unique(a, return_index = True) 
indices

# 去重数组的下标
u,indices = np.unique(a,return_inverse = True) 
u
indices

# 返回去重元素的重复数量 
u,indices = np.unique(a,return_counts = True) 
u
indices

numpy.clip()

t.clip(10,18)
# 小于10的替换成10，大于18的替换成18

#这是jupyter notebook的笔记
import numpy as np

t=np.arange(24).reshape(4,6)
t


#元素删除：numpy.delete()
array02

np.delete(array02,2)

np.delete(array02,[2,4,6,8])

np.delete(array02,2,axis=0)

#数组元素去重numpy.unique()
array03=np.array([[0,11,22,3,4,5],
                [11,12,13,14,15,11],
                [11,12,13,14,15,11],
                [18,16,20,21,15,23]])
array03

#np.unique(array03,axis=0)#意思是两行元素完全相同的时候才算做重复

np.unique(array03,return_inverse=True,axis=0)#意思是两行元素完全相同的时候才算做重复

array03#说明什么视图与本质还是有区别的

np.unique(array03,return_index=True,axis=0)#意思是两行元素完全相同的时候才算做重


np.unique(array03,return_counts=True,axis=0)#意思是两行元素完全相同的时候才算做重复

#数组的裁减numpy.clip()
array03

np.clip(array03,12,20)#小于12的都变成了12 ，大于20的都变成了20


array03

np.clip(array03,12,20,out=array03)#小于12的都变成了12 ，大于20的都变成了20


array03#说明啥子，使用out以后原数组也变了,就地裁剪。

d.数组的行列转换、迭代，转置

t[[1, 2], :] = t[[2, 1], :] # 行列交换

t[: ,[0, 2]] = t[: ,[2, 0]] # 列交换

import numpy as np

array01=np.arange(24).reshape(4,6)
array01

array01[[0,1],:]=array01[[1,0],:]#行交换
array01


array01[:,[2,3]]=array01[:,[3,2]]#列的交换
array01#原理：x,y=y,x

#迭代数组

array01.shape

array01.ndim

#；利用flat扁平化一位数组，然后遍历、迭代
for item in array01.flat:#二维数组的迭代
    print(item)

for i in range(array01.size):
    print(array01.flat[i])

for item in np.nditer(array01):#相当于array01.flat
    print(item)

#for...for 循环
for item in array01:
    print(item)
    

for items in array01:#嵌套循环
    for item in items:
        print(item)

转置：np.transpose()、array.T、rollaxis()、swapaxes()

# 数组的转置
array01
array01.T#行列的变换
np.transpose(array01,axes=(1,0))
np.transpose(array01,axes=(0,1))

e.连接和分割数组

连接：numpy.concatenate()、numpy.column_stack()、numpy.row_stack()

连接：numpy.stack()、numpy.hstack()、numpy.vstack、numpy.dstack()、numpy.pad()

垂直方向操作：vstack()

import numpy as np
a = np.arange(1, 7).reshape(2, 3)
b = np.arange(7, 13).reshape(2, 3)
a,b

# 垂直方向完成组合操作，生成新数组
c = np.vstack((a, b))

# 垂直方向完成拆分操作，生成两个数组
d, e = np.vsplit(c, 2)

水平方向操作：hstack()

import numpy as np
a = np.arange(1, 7).reshape(2, 3)
b = np.arange(7, 13).reshape(2, 3)
a,b

# 水平方向完成组合操作，生成新数组 
c = np.hstack((a, b))

# 水平方向完成拆分操作，生成两个数组
d, e = np.hsplit(c, 2)

深度方向操作：dstack()（3维）

import numpy as np
a = np.arange(1, 7).reshape(2, 3)
b = np.arange(7, 13).reshape(2, 3)
a,b

# 深度方向（3维）完成组合操作，生成新数组
i = np.dstack((a, b))

# 深度方向（3维）完成拆分操作，生成两个数组
k, l = np.dsplit(i, 2)

长度不等的数组组合：

import numpy as np
a = np.array([1,2,3,4,5])
b = np.array([1,2,3,4])
a,b

# 填充b数组使其长度与a相同
b = np.pad(b, pad_width=(0, 1), mode='constant', constant_values=-1)
b

# 垂直方向完成组合操作，生成新数组
c = np.vstack((a, b))
c

多维数组组合与拆分的相关函数：

# 通过axis作为关键字参数指定组合的方向，取值如下：
# 若待组合的数组都是二维数组：
#	0: 垂直方向组合
#	1: 水平方向组合
# 若待组合的数组都是三维数组：
#	0: 垂直方向组合
#	1: 水平方向组合
#	2: 深度方向组合
np.concatenate((a, b), axis=0)
# 通过给出的数组与要拆分的份数，按照某个方向进行拆分，axis的取值同上
np.split(c, 2, axis=0)

简单的一维数组组合方案

a = np.arange(1,9)		
b = np.arange(9,17)	
#把两个数组摞在一起成两行
c = np.row_stack((a, b))
c

#把两个数组组合在一起成两列
d = np.column_stack((a, b))
d

分割：numpy.split()、numpy.hsplit()、numpy.vsplit()、numpy.dsplit()

将一个数组拆分为几个较小的数组

hsplit # 沿数组的水平轴拆分数组
vsplit # 沿数组的垂直轴拆分数组
array_split # 指定沿哪个轴分割

上述jupyter的代码笔记如下
#连接数组num

import numpy as np

array01=np.arange(24).reshape(4,6)
array01

array02 = np.arange(24).reshape(4,6)
array02

np.concatenate((array01,array02),axis=0) #按照列的个数匹配链接

np.concatenate((array01,array02),axis=1) #按照列的个数匹配链接


#numpy.column_stack(*args,**kwargs)
np.column_stack((array01,array02))

np.row_stack((array01,array02))

#np.dstack(a1,a2)
np.dstack((array01,array02))

#分割数组：

#水平切
np.hsplit(array01,2)

array01

array04,array05,array06=np.hsplit(array01,3)

array04

array05

array06

#垂直切(与上面同理)
np.vsplit(array02,2)


#沿深度切
#np.dstack(a1,a2)
array03=np.dstack((array01,array02))
array03

array04,array05=np.vsplit(array03,2)

array04

array05

7.数组运算

a.数组运算的通用函数

函数	说明
numpy.sqrt(array)	平方根函数
numpy.exp(array)	e^array[i]的数组
numpy.abs/fabs(array)	计算绝对值
numpy.square(array)	计算各元素的平方 等于array**2
numpy.log/log10/log2(array)	计算各元素的各种对数
numpy.sign(array)	计算各元素正负号
numpy.isnan(array）	计算各元素是否为NaN
numpy.isinf(array)	计算各元素是否为无穷大
numpy.cos/cosh/sin/sinh/tan/tanh(array)	三角函数
numpy.modf(array)	将array中值得整数和小数分离，作两个数组返回
numpy.ceil(array)	向上取整,也就是取比这个数大的整数
numpy.floor(array)	向下取整,也就是取比这个数小的整数
numpy.rint(array)	四舍五入
numpy.trunc(array)	向0取整
numpy.add(array1,array2)	元素级加法
numpy.subtract(array1,array2)	元素级减法
numpy.multiply(array1,array2)	元素级乘法
numpy.divide(array1,array2)	元素级除法 array1./array2
numpy.power(array1,array2)	元素级指数 array1.^array2
numpy.maximum/minimum(array1,aray2)	元素级最大值、最小值
numpy.fmax/fmin(array1,array2)	元素级最大值，最小值（忽略NaN）
numpy.mod(array1,array2)	元素级求模
numpy.mod(array1,array2)	元素级求模
numpy.copysign(array1,array2)	将第二个数组中值得符号复制给第一个数组中值

b.广播机制

广播(Broadcast)是 numpy 对不同形状(shape)的数组进行数值计算的方式， 对数组的算术运算通常在相应的元素上进行。

当运算中的 2 个数组的形状不同时，numpy 将自动触发广播机制:

import numpy as np 
 
a = np.array([[ 0, 0, 0],
           [10,10,10],
           [20,20,20],
           [30,30,30]])
b = np.array([1,2,3])
a + b

广播的规则:

• 让所有输入数组都向其中形状最长的数组看齐，形状中不足的部分都通过在前面加 1 补齐。
• 输出数组的形状是输入数组形状的各个维度上的最大值。
• 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时，这个数组能够用来计算，否则出错。
• 当输入数组的某个维度的长度为 1 时，沿着此维度运算时都用此维度上的第一组值。

b.数组的算数运算

数组和数的运算

numpy的广播机制在运算过程中，加减乘除的值被广播到所有的元素上。

t1 = np.arange(24).reshape(6,4) 
t1+2 
t1*2
t1/2
t1-2

数组与数组的运算

同种形状的数组(对应位置进行计算操作)

如果两个数组 a 和 b 形状相同，即满足 a.shape == b.shape，那么 a*b 的结果就是 a 与 b 数组对应位相乘。这要求维数(ndim)相同，且各维度的长度(shape)相同。

t1 = np.arange(24).reshape((6,4)) 
t2 = np.arange(100,124).reshape((6,4)) 
t1+t2
t1*t2
t1-t2
t1/t2

不种形状的多维数组计算

# 行数不同，列数相同，不能进行算术运算
t1 = np.arange(24).reshape((4,6)) 
t2 = np.arange(18).reshape((3,6)) 
t1
t2 
t1-t2
# 提示什么错误？
# ValueError: operands could not be broadcast together with shapes (4,6) (3,6)

# 行数相同，列数不同，可以进行运算
t1 = np.arange(24).reshape((4,6)) 
t2 = np.arange(4).reshape((4,1)) 
t1-t2

行数或者列数相同的一维数组和多维数组可以进行计算:

​ 列形状相同（会与每一个相同维度的数组的对应位相操作)

t1 = np.arange(24).reshape((4,6)) 
t2 = np.arange(0,6) 
t1-t2

​ 行形状相同（会与每一个相同维度的数组的对应位相操作)

行数相同时数组为二维数组

数组上的算术运算符适用于elementwise（对应位置元素逐个相乘）

import numpy

a = np.array([20,30,40,50])
b = np.arange(4)

# 算术运算
c = a - b
c #?

b ** 2 #?

10 * np.sin(a) #?

增强运算

某些操作（例如+=和）*=就位以修改现有数组，而不是创建一个新数组

rg = np.random.default_rng(1)
a = np.ones((2,3),dtype=int)
b = rg.random((2,3))
a*3
a #?

b += a
b #?

a += b

也可以看看,其他有关数学运算的函数：

all， any， apply_along_axis， argmax， argmin， argsort， average， bincount， ceil， clip， conj， corrcoef， cov， cross， cumprod， cumsum， diff， dot， floor， inner， invert， lexsort， max， maximum， mean， median， min， minimum， nonzero， outer， prod， re， round， sort， std， sum， trace， transpose， var， vdot， vectorize， where

c.矩阵运算

与许多矩阵语言不同，乘积运算符*在NumPy数组中按元素进行操作。可以使用@运算符（在python> = 3.5中）或dot函数或方法执行矩阵乘积：

   a = np.array([[1,1],[0,1]])
   b = np.array([[2,0],[3,4]])
   
   a * b #？
   
   a @ b #？

   a.dot(b) #？

d.数学函数

通用功能：NumPy提供了熟悉的数学函数，例如sin，cos和exp。在NumPy中，这些被称为“通用函数”（ufunc）。在NumPy中，这些函数在数组上逐个元素操作，生成数组作为输出。

b = np.arange(3)
np.exp(b)
np.sqrt(b)

c = np.array([2.,-1.,1.41421356])
np.add(b,c) #?

e.统计函数

函数	说明
np.sum()	计算数组的和
np.mean()	返回数组中元素的算术平均值
np.average()	根据在另一个数组中给出的各自的权重计算数组中元素的加权平均值
np.std()	计算数组标准差
np.var()	计算数组方差
np.min()	计算数组中的元素沿指定轴的最小值
np.max()	计算数组中的元素沿指定轴的最大值
np.argmin()	返回数组最小元素的索引
np.argmax()	返回数组最大元素的索引
np.cumsum()	计算所有元素的累计和
np.cumprod()	计算所有元素的累计积
np.ptp()	计算数组中元素最大值与最小值的差（最大值 - 最小值）
np.median()	计算数组中元素的中位数（中值）

import numpy as np 

score = np.array([[80,88],[82,81],[75,81]]) 

# 1. 获取所有数据最大值 
result = np.max(score) 

# 2. 获取某一个轴上的数据最大值 
result = np.max(score,axis=0) 

# 3. 获取最小值 
result = np.min(score)

# 4. 获取某一个轴上的数据最小值
result = np.min(score,axis=0) 

# 5. 数据的比较 
result = np.maximum([-2, -1, 0, 1, 2], 0) # 第一个参数中的每一个数与第二个参数比较返回大的
result = np.minimum([-2, -1, 0, 1, 2], 0) # 第一个参数中的每一个数与第二个参数比较返回小的
result = np.maximum([-2, -1, 0, 1, 2], [1,2,3,4,5]) # 接受的两个参数，也可以大小一致; 第二个参数只是一个单独的值时，其实是用到了维度的广播机制； 

# 6. 求平均值 
result = np.mean(score) # 获取所有数据的平均值 
result = np.mean(score,axis=0) # 获取某一行或者某一列的平均值

# 7. 返回给定axis上的累计和 
arr = np.array([[1,2,3], [4,5,6]]) 
arr
arr.cumsum(0) 
arr.cumsum(1)

# 8. argmin求最小值索引 
result = np.argmin(score,axis=0) 
result

# 9. 求每一列的标准差 
# 标准差是一组数据平均值分散程度的一种度量。一个较大的标准差，代表大部分数值和其平均值之间差异较大；
# 一个较小的标准差，代表这些数据较接近平均值反应出数据的波动稳定情况，越大表示波动越大，越不稳 定。
result = np.std(score,axis=0) 
result 

# 10. 极值 
# np.ptp(t,axis=None)就是最大值和最小值的差 
# 拓展：方差var, 协方差cov, 计算平均值 average, 计算中位数 median

numpy.argmax() 和 numpy.argmin()函数分别沿给定轴返回最大和最小元素的索引：

import numpy as np 
 
a = np.array([[30,40,70],[80,20,10],[50,90,60]])  
a


# 调用 argmax() 函数
np.argmax(a)

# 展开数组：
a.flatten()

# 沿轴 0 的最大值索引
maxindex = np.argmax(a, axis=0)  
maxindex

# 沿轴 1 的最大值索引： 
maxindex = np.argmax(a, axis=1)  
maxindex 

# 调用 argmin() 函数：
minindex = np.argmin(a)  
minindex

# 展开数组中的最小值： 
a.flatten()[minindex]
 
# 沿轴 0 的最小值索引： 
minindex = np.argmin(a, axis=0)  
minindex

# 沿轴 1 的最小值索引：
minindex = np.argmin(a, axis=1)  
minindex

f.字符串函数

对 dtype 为 numpy.string_ 或 numpy.unicode_ 的数组执行向量化字符串操作。

这些函数在字符数组类（numpy.char）中定义

函数	描述
add()	对两个数组的逐个字符串元素进行连接
multiply()	返回按元素多重连接后的字符串
center()	居中字符串
capitalize()	将字符串第一个字母转换为大写
title()	将字符串的每个单词的第一个字母转换为大写
lower()	数组元素转换为小写
upper()	数组元素转换为大写
split()	指定分隔符对字符串进行分割，并返回数组列表
splitlines()	返回元素中的行列表，以换行符分割
strip()	移除元素开头或者结尾处的特定字符
join()	通过指定分隔符来连接数组中的元素
replace()	使用新字符串替换字符串中的所有子字符串
decode()	数组元素依次调用str.decode
encode()	数组元素依次调用str.encode

numpy.char.add() # 函数依次对两个数组的元素进行字符串连接
numpy.char.multiply() # 函数执行多重连接
numpy.char.center() # 函数用于将字符串居中，并使用指定字符在左侧和右侧进行填充
numpy.char.capitalize() # 函数将字符串的第一个字母转换为大写
numpy.char.title() # 函数将字符串的每个单词的第一个字母转换为大写
numpy.char.lower() # 函数对数组的每个元素转换为小写。它对每个元素调用 str.lower
numpy.char.upper() # 函数对数组的每个元素转换为大写。它对每个元素调用 str.upper
numpy.char.split() # 通过指定分隔符对字符串进行分割，并返回数组。默认情况下，分隔符为空格
numpy.char.splitlines() # 函数以换行符作为分隔符来分割字符串，并返回数组
numpy.char.strip() # 函数用于移除开头或结尾处的特定字符
numpy.char.join() # 函数通过指定分隔符来连接数组中的元素或字符串
numpy.char.replace() # 函数使用新字符串替换字符串中的所有子字符串
numpy.char.encode() # 函数对数组中的每个元素调用 str.encode 函数。 默认编码是 utf-8，可以使用标准 Python 库中的编解码器
numpy.char.decode() # 函数对编码的元素进行 str.decode() 解码

g.排序函数

numpy.sort() 函数返回输入数组的排序副本

numpy.sort(a, axis, kind, order)

参数	说明
a	要排序的数组
axis	沿着它排序数组的轴
kind	默认为（快速排序）
order	如果数组包含字段，则是要排序的字段

import numpy as np  
 
a = np.array([[3,7],[9,1]])  
a

print ('调用 sort() 函数：')
np.sort(a)

np.sort(a, axis=0)
np.sort(a, axis=1)

# 在 sort 函数中排序字段 
dt = np.dtype([('name',  'S10'),('age',  int)]) 
a = np.array([("raju",21),("anil",25),("ravi",  17),  ("amar",27)], dtype = dt)  
a
np.sort(a, order='name')

h.条件筛选函数

g.文件读写

NumPy文件读写主要有二进制的文件读写和文件列表形式的数据读写两种形式

np.loadtxt(fname,dtype=np.float,delimiter=None,skiprows=0,usecols=None,unpack=False)

参数	说明
fname	文件，字符串或产生器，可以是.gz或bz2压缩文件
dtype	数据类型，可选，默认为np.float
delimiter	分隔字符串，默认是任何空格，改为逗号
skiprows	跳过前x行，一般跳过第一行表头
usecols	读取指定的列，索引，元组类型
unpack	如果为True,读入属性将分别写入不同数组变量，False读入数据只写入一个数组变量，默认False

三、numpy-矩阵专题

矩阵是numpy.matrix类型的对象，该类继承自numpy.ndarray，任何针对多维数组的操作，对矩阵同样有效，但是作为子类矩阵又结合其自身的特点，做了必要的扩充，比如：乘法计算、求逆等。

1. 矩阵对象的创建

# 等价于：numpy.matrix(..., copy=False)
# 由该函数创建的矩阵对象与参数中的源容器一定共享数据，无法拥有独立的数据拷贝
numpy.mat(任何可被解释为矩阵的二维容器)

# 该函数可以接受字符串形式的矩阵描述：
# 数据项通过空格分隔，数据行通过分号分隔。例如：'1 2 3; 4 5 6'
numpy.mat(拼块规则)

示例：创建matrix

# 创建matrix操作
import numpy as np

arr = np.arange(1, 10).reshape(3, 3)
arr

# 第一种方式
m = np.matrix(arr, copy=True)
m
m.shape
type(m)

# 第二种方式:共享方式
m2 = np.mat(arr)
m2

# 第三种方式
m3 = np.mat("1 2 3;4 5 6.0")
m3

2. 矩阵的乘法运算

# 矩阵乘法
import numpy as np

arr = np.array([[1, 1, 1],
                [2, 2, 2],
                [3, 3, 3]])

# 数组相乘, 各对应位置元素相乘
arr * arr

# 矩阵相乘，第n行乘m列之和，作为结果的n, m个元素
# 矩阵相乘，第一个矩阵列数必须等于第二个矩阵行数
m = np.mat(arr)
m * m

3. 矩阵的逆矩阵

若两个矩阵A、B满足：AB = E （E为单位矩阵），则称B为A的逆矩阵。

单位矩阵

在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1，这种矩阵被称为单位矩阵。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1，除此以外全都为0，记为$I_n$或$E_n$ ，通常用I或E来表示。根据单位矩阵的特点，任何矩阵与单位矩阵相乘都等于本身，而且单位矩阵因此独特性有广泛用途。以下是一个单位矩阵示例：
$$E_3=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
逆矩阵示例：

e = np.mat("1 2 6; 3 5 7; 4 8 9")
print(e.I)
print(e * e.I)

注意：在计算过程中，可能出现如下错误，说明该矩阵不可逆。

numpy.linalg.LinAlgError: Singular matrix

4. ndarray提供的矩阵API

ndarray提供了方法让多维数组替代矩阵的运算：

a = np.array([
    [1, 2, 6],
    [3, 5, 7],
    [4, 8, 9]])

# 点乘法求ndarray的点乘结果，与矩阵的乘法运算结果相同
k = a.dot(a)
k

# linalg模块中的inv方法可以求取a的逆矩阵
l = np.linalg.inv(a)
l

5. 矩阵应用

案例：解线性方程组

假设一帮孩子和家长出去旅游，去程坐的是bus，小孩票价为3元，家长票价为3.2元，共花了118.4；回程坐的是Train，小孩票价为3.5元，家长票价为3.6元，共花了135.2。分别求小孩和家长的人数。使用矩阵求解。表达成方程为：

$$\begin{gathered} 3x+3.2y=118.4 \\ 3.5x+3.6y=135.2 \end{gathered}$$

表示成矩阵相乘：

$$\left[\begin{array}{cc}3& 3.2\\ 3.5& 3.6\end{array}\right]\times \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}118.4\\ 135.2\end{array}\right]$$

import numpy as np

# 解方程
prices = np.mat('3 3.2; 3.5 3.6')
totals = np.mat('118.4; 135.2')

x = np.linalg.lstsq(prices, totals)[0]  # 求最小二乘解
x

x = np.linalg.solve(prices, totals)  # 求解线性方程的解
x

x = prices.I * totals  # 利用矩阵的逆进行求解
x

四、numpy-概率论专题

numpy提供了random模块生成服从特定统计规律的随机数序列

1.随机抽样(np.random)

函数	描述
np.random.randint（）	返回随机整数，左闭右开区间 [low, high)
np.random.randn()	返回一个样本，具有标准正态分布
np.random.rand()	随机样本位于[0, 1)中
np.random.random_integers()	返回随机的整数，位于闭区间 [low, high]
np.random.random_sample()	返回随机的浮点数，在半开区间 [0.0, 1.0)
np.random.random()	返回随机的浮点数，在半开区间 [0.0, 1.0)
np.random.ranf()	返回随机的浮点数，在半开区间 [0.0, 1.0)
np.random.sample()	返回随机的浮点数，在半开区间 [0.0, 1.0)
np.random.choice()	生成一个随机样本
np.random.bytes()	返回随机字节

2.排列

函数	描述
np.random.shuffle(array)	随机打乱顺序
np.random.permutation(array)	返回一个随机排列

3.分布

函数	描述
binomial(n,p[,size])	二项分布的样本
exponential([scale,size])	指数分布
f((dfnum, dfden[, size]))	F分布样本
geometric(p[, size])	几何分布
hypergeometric(ngood, nbad, nsample[, size])	超几何分布样本
multinomial(n, pvals[, size])	多项分布
normal([loc, scale, size])	正态(高斯)分布
pareto(a[, size])	帕累托（Lomax）分布
poisson([lam, size])	泊松分布
standard_normal([size])	标准正态分布 (mean=0, stdev=1).
uniform([low, high, size])	均匀分布