蓝桥杯2017年第八届C/C++ B组省赛习题题解
目录
第一题:购物单(暴力计算)
第二题:等差素数数列(数学+暴力枚举)
第三题:承压计算(模拟)
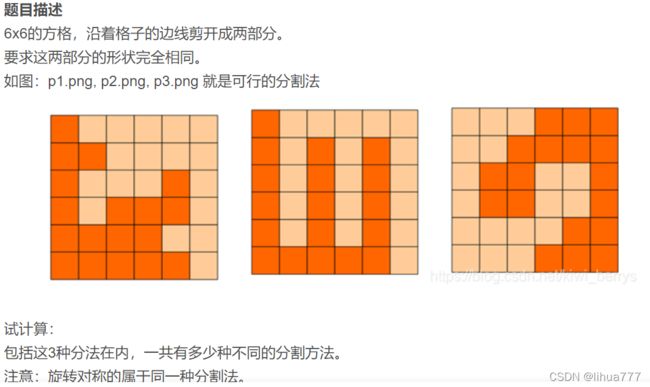
第四题:方格分割(dfs)
第五题:取数位(模拟)
第六题:最大公共子串(dp)
第七题:日期问题(暴力枚举)
第八题:包子凑数(完全背包+数论)
第九题:分巧克力(二分)
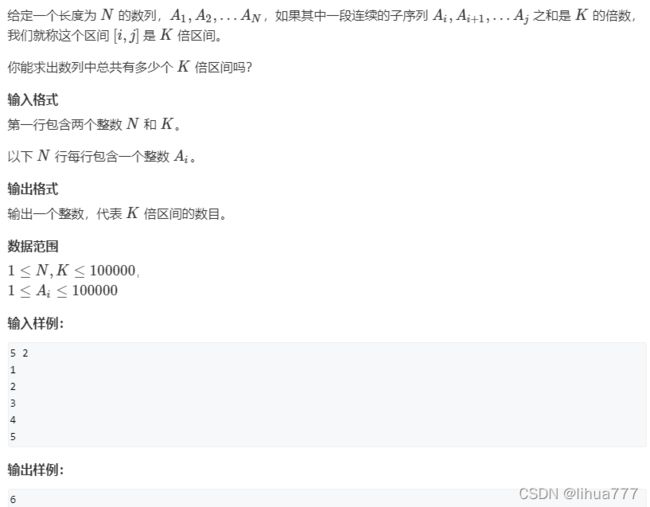
第十题:k倍区间(前缀和+同余定理)
题目来源:
2017年第八届C/C++ B组蓝桥杯省赛真题_元气算法的博客-CSDN博客
第一题:购物单(暴力计算)
核心思路:
多次输入,数据向上取整,打折价格为:
原价格为a,打折率为:b/100,二者相乘,用sum累加即可,最后如果不放心可以对其进行取整
#include
#include
using namespace std;
int main()
{
float a;
int b;
float sum = 0;
while(scanf("**** %f %d\n",&a,&b))
{
sum += a*b/100;
}
printf("%f",sum);//5200
}
第二题:等差素数数列(数学+暴力枚举)
#include
using namespace std;
long long int prime[100019];
bool isprime(long long int n)
{
for (long long int i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
int main()
{
for (long long int i = 2; i <= 100009; i++) //素数打表
if (isprime(i))
prime[i] = 1;
for (int i = 1; i <= 1000; i++) //枚举公差
for (int j = 1; j <= 8000; j++)
{ // 枚举首项
int flag = 0;
for (int k = 1; k <= 9; k++)
{
if (prime[j + k * i] == 0)
{
flag = 1;
break;
}
}
if (!flag)
{
printf("%d\n", i);
return 0;
}
}
return 0;
}
第三题:承压计算(模拟)
7
5 8
7 8 8
9 2 7 2
8 1 4 9 1
8 1 8 8 4 1
7 9 6 1 4 5 4
5 6 5 5 6 9 5 6
5 5 4 7 9 3 5 5 1
7 5 7 9 7 4 7 3 3 1
4 6 4 5 5 8 8 3 2 4 3
1 1 3 3 1 6 6 5 5 4 4 2
9 9 9 2 1 9 1 9 2 9 5 7 9
4 3 3 7 7 9 3 6 1 3 8 8 3 7
3 6 8 1 5 3 9 5 8 3 8 1 8 3 3
8 3 2 3 3 5 5 8 5 4 2 8 6 7 6 9
8 1 8 1 8 4 6 2 2 1 7 9 4 2 3 3 4
2 8 4 2 2 9 9 2 8 3 4 9 6 3 9 4 6 9
7 9 7 4 9 7 6 6 2 8 9 4 1 8 1 7 2 1 6
9 2 8 6 4 2 7 9 5 4 1 2 5 1 7 3 9 8 3 3
5 2 1 6 7 9 3 2 8 9 5 5 6 6 6 2 1 8 7 9 9
6 7 1 8 8 7 5 3 6 5 4 7 3 4 6 7 8 1 3 2 7 4
2 2 6 3 5 3 4 9 2 4 5 7 6 6 3 2 7 2 4 8 5 5 4
7 4 4 5 8 3 3 8 1 8 6 3 2 1 6 2 6 4 6 3 8 2 9 6
1 2 4 1 3 3 5 3 4 9 6 3 8 6 5 9 1 5 3 2 6 8 8 5 3
2 2 7 9 3 3 2 8 6 9 8 4 4 9 5 8 2 6 3 4 8 4 9 3 8 8
7 7 7 9 7 5 2 7 9 2 5 1 9 2 6 5 3 9 3 5 7 3 5 4 2 8 9
7 7 6 6 8 7 5 5 8 2 4 7 7 4 7 2 6 9 2 1 8 2 9 8 5 7 3 6
5 9 4 5 5 7 5 5 6 3 5 3 9 5 8 9 5 4 1 2 6 1 4 3 5 3 2 4 1
X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X
解题思路:
第八届蓝桥杯 ——承压计算_业余算法学徒的博客-CSDN博客
核心:递推模拟
为什么要求最小值???
因为单位的不同,因此无法正确的数字,比如7无法正常从推出5 和 8,所以我们要求出单位
单位的求法就是:题目给出了最小值,所以我们也要计算出我们得出的最小值,这样就可以得到了单位,再用这个单位去乘以最大值,就得到了题目的正确所求最大值
#include
#include
using namespace std;
double g[40][40];
int main()
{
for (int i = 1; i <= 30; i ++)
for (int j = 1; j <= i; j ++)
scanf("%lf", &g[i][j]);
for (int i = 1; i <= 29; i ++)
for (int j = 1; j <= i; j ++)
{
g[i + 1][j] += g[i][j] / 2;
g[i + 1][j + 1] += g[i][j] / 2;
}
double maxv = 0, minv = 0x7f7f7f7f;//一个很大的值
for (int i = 1; i <= 30; i ++)
{
maxv = max(maxv, g[30][i]);
minv = min(minv, g[30][i]);
}
printf("%f", 2086458231 / minv * maxv);
return 0;
}
第四题:方格分割(dfs)
题目分析:
从整张图的中心点出发, 每当一边切割一下时,相对的另一边也要切割相对的一下,当到达边界时候,就会对称,注意最后出来的结果要除以4,应为有4次重复
#include
using namespace std;
int vis[10][10] = { 0 };
int dir[4][2] = { {1,0},{-1,0},{0,1},{0,-1} };
int ans = 0;
void dfs(int x, int y)
{
if (!x || !y || x == 6 || y == 6)//如果已经走过,且到边界了
{
ans++;
return;
}
for (int i = 0; i < 4; i++)
{
int tempx = x + dir[i][0];
int tempy = y + dir[i][1];
if (!vis[tempx][tempy])
{
vis[tempx][tempy] = 1;
vis[6 - tempx][6 - tempy] = 1;//对称标记
dfs(tempx, tempy);
vis[tempx][tempy] = 0;//还原现场
vis[6 - tempx][6 - tempy] = 0;//还原现场
}
}
}
int main()
{
vis[3][3] = 1;
dfs(3, 3);
cout << ans / 4 << endl;
return 0;
} 第五题:取数位(模拟)
#include
#include
using namespace std;
int len(int x)//求数字的长度
{
if (x < 10) return 1;
return len(x / 10) + 1;
}
// 取x的第k位数字
int f(int x, int k)
{
if (len(x) - k == 0) return x % 10;
return f(x / 10, k); //填空
}
int main()
{
int x = 23574;
//printf("%d\n", 23574 % 5);
printf("%d\n", f(x, 5));
return 0;
}
第六题:最大公共子串(dp)
#include
#include
#include
using namespace std;
const int N = 256;
int f(const char* s1, const char* s2)
{
int dp[N][N];
int len1 = strlen(s1);
int len2 = strlen(s2);
memset(dp, 0, sizeof(int) * N * N);
int max = 0;
for (int i = 1; i <= len1; i++)
{
for (int j = 1; j <= len2; j++)
{
if (s1[i - 1] == s2[j - 1])
{
dp[i][j] = dp[i - 1][j - 1] + 1; //填空
if (dp[i][j] > max) max = dp[i][j];
}
}
}
return max;
}
int main()
{
printf("%d\n", f("abcdkkk", "baabcdadabc"));
return 0;
}
第七题:日期问题(暴力枚举)
活动 - AcWing
核心思路:枚举日期,判断其是否合法即可
#include
#include
#include
#include
using namespace std;
int days[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
bool check_valid(int year, int month, int day)
{
if (month == 0 || month > 12) return false;
if (day == 0) return false;
if (month != 2)
{
if (day > days[month]) return false;
}
else
{
int leap = year % 100 && year % 4 == 0 || year % 400 == 0;
if (day > 28 + leap) return false;
}
return true;
}
int main()
{
int a, b, c;
scanf("%d/%d/%d", &a, &b, &c);
for (int date = 19600101; date <= 20591231; date ++ )
{
int year = date / 10000, month = date % 10000 / 100, day = date % 100;
if (check_valid(year, month, day))
{
if (year % 100 == a && month == b && day == c || // 年/月/日
month == a && day == b && year % 100 == c || // 月/日/年
day == a && month == b &&year % 100 == c) // 日/月/年
printf("%d-%02d-%02d\n", year, month, day);
}
}
return 0;
} 第八题:包子凑数(完全背包+数论)
写过--->>不再赘述
#include
#include
using namespace std;
const int N = 10010;
int a[110];
bool f[110][N];
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int main()
{
int n;
scanf("%d", &n);
int d = 0;
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
d = gcd(d, a[i]);
}
if (d != 1) puts("INF");
else
{
f[0][0] = true;
for (int i = 1; i <= n; i++)
for (int j = 0; j < N; j++)
{
f[i][j] = f[i - 1][j];
if (j >= a[i]) f[i][j] |= f[i][j - a[i]];
}
int res = 0;
for (int i = 0; i < N; i++)
if (!f[n][i])
res++;
printf("%d\n", res);
}
return 0;
} 第九题:分巧克力(二分)
写过
#include
#include
#include
using namespace std;
const int N=100010;
int h[N],w[N];
int n,k;
bool check(int mid)
{
int res=0;
for(int i=0;i=k) return true;
}
return false;
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=0;i>1;
if(check(mid)) left=mid;
else right=mid-1;
}
cout< 第十题:k倍区间(前缀和+同余定理)
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N = 100010;
/*没讲清楚,为什么前缀和模为1的时候会影响模为0的值,我认为是这样:总共出现了3次模为1的情况,
而每两次模为1组合起来可以模0,比如1,2加起来模为1,1,2,3,4,5加起来模为1,那么这两种情况组合起
来(区间做减)是3,4,5就是模为0的情况。所以一共出现了3次模为1的情况,那么两两组合的情况一共有三种,再
加上本来模为0的情况有3次,一共就6次模为0的情况。“k倍区间就加上cnt[sum[i]]”只是实现了计算模不为0的时候
的情况两两组合的组合数量*/
//答案等于前缀中出现过的和s[i]余k相等的计数之和,完成答案的计算之后需要将计数数组更新,加上自己
int n, k;
ll s[N], cnt[N];
int main()
{
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++)
{
scanf("%lld", &s[i]);
s[i] += s[i - 1];
}
ll res = 0;
cnt[0] = 1;
for (int i = 1; i <= n; i++)
{
res += cnt[s[i] % k];//已经构造好了:
cnt[s[i] % k]++;
}
cout << res << endl;
return 0;
}