【2021年蓝桥省赛真题】赛前最后冲刺，省一我来啦
作者简介：大家好，我是Ceylan_，可以叫我CC ❣️
个人主页：Ceylan_的博客
博主信息：平凡的大一学生，有着不平凡的梦⚡希望大家多多支持一起进步~❤️
若有帮助，还请关注➕点赞➕收藏，不行的话我再努努力
目录
第一题 空间
❓问题描述
题目分析
代码演示
第二题 卡片
❓问题描述
题目分析
代码演示
第三题 直线
❓问题描述
题目分析
代码演示
第四题 货物摆放
❓问题描述
题目分析
代码演示
第五题 路径
❓问题描述
题目分析
代码演示
第六题 时间显示
❓问题描述
题目分析
代码演示
第七题 砝码称重
❓问题描述
题目分析
代码演示
第八题 杨辉三角形
❓问题描述
题目分析
代码演示
第九题 双向排序
❓问题描述
题目分析
代码演示
第十题 括号序列
❓问题描述
题目分析
总结
第一题 空间
❓问题描述
小蓝准备用 256MB 的内存空间开一个数组，数组的每个元素都是 32 位 二进制整数，如果不考虑程序占用的空间和维护内存需要的辅助空间，请问 256MB 的空间可以存储多少个 32 位二进制整数？
题目分析
1MB=1024KB 1KB=1024字节 1字节=8位
代码演示
#include
using namespace std;
int main()
{
cout<<256*1024*1024*8/32;
return 0;
} 第二题 卡片
❓问题描述
小蓝有很多数字卡片，每张卡片上都是数字 0 到 9。 小蓝准备用这些卡片来拼一些数，他想从 1 开始拼出正整数，每拼一个， 就保存起来，卡片就不能用来拼其它数了。 小蓝想知道自己能从 1 拼到多少。 例如，当小蓝有 30 张卡片，其中 0 到 9 各 3 张，则小蓝可以拼出 1 到 10， 但是拼 11 时卡片 1 已经只有一张了，不够拼出 11。 现在小蓝手里有 0 到 9 的卡片各 2021 张，共 20210 张，请问小蓝可以从 1 拼到多少？
题目分析
从1开始拼，由数学规律可得，1是最快被拼完的数字，只需统计1出现的次数，就能得到答案。
代码演示
#include
using namespace std;
int main()
{
int i=0;
int sum=2021;
int b=0;
for(i=1;i<20210;i++)
{
int c=i;
while(c)
{
b=c%10;
if(b==1&&sum>0)
{
sum--;
}
c/=10;
}
if (sum==0)
{
break;
}
}
cout< 第三题 直线
❓问题描述
在平面直角坐标系中，两点可以确定一条直线。如果有多点在一条直线上，那么这些点中任意两点确定的直线是同一条。
给定平面上2×3个整点{(x，y)|0≤x<2，0≤y<3，xZ，y
给定平面上20×21个整点{(x，y)|0≤x<20.0≤y<21，x
题目分析
两点确定一条直线，我们可以记录每一种情况，然后判断是否重复。
直线一共三种情况
第一种，横直线，一共20种
第二种，竖直线，一共21种
第三种，斜直线，这种直线可由y=kx+b来表示，也就是说【k，b】可以表示一条直线
代码演示
#include
using namespace std;
map,int> mp;
struct Point
{
double x,y;
}p[25*25];
int main()
{
int cnt=0;
for(int i=0;i<20;i++)
{
for(int j=0;j<21;j++)
{
p[cnt].x=i;
p[cnt].y=j;
++cnt;
}
}
int ans=0;
for(int i=0;i 第四题 货物摆放
❓问题描述
小蓝有一个超大的仓库，可以摆放很多货物。
现在，小蓝有 n 箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆 L、W、H 的货物,满足 n=L×W×H。
给定 n，请问有多少种堆放货物的方案满足要求。
例如，当 n=4 时，有以下 6 种方案：1×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1.
请问，当 n=2021041820210418（注意有 16 位数字）时，总共有多少种方案？
题目分析
暴力枚举每种符合条件的长宽高
当三边相等时，只有一种拼法，ans++
当两边相等时，有三种拼法，ans+=3
当三边不相等时，有六种拼法，ans+=6
代码演示
#include
using namespace std;
int main()
{
long long n=2021041820210418;
long long i,j,k;
int ans=0;
for(i=1;i*i*i<=n;i++)
{
if(n%i==0)
{
for(j=i;i*j*j<=n;j++)
{
if(n/i%j==0)
{
k=n/i/j;
if(i==j&&i==k) ans++;
if(i==j||i==k||j==k) ans+=3;
else ans+=6;
}
}
}
}
cout< 第五题 路径
❓问题描述
小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图 中的最短路径。
小蓝的图由 2021 个结点组成，依次编号 1 至 2021。
对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点 之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条 长度为 a 和 b 的最小公倍数的无向边相连。
例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无 向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为 75。
请计算，结点 1 和结点 2021 之间的最短路径长度是多少。
题目分析
最短路问题，想到了动态规划（孩子不会Floyd算法或DijkStra算法）
使用f[i]数组，表述从1到i所用的最短长度，每一次循环更新该点能到达位置的最短位置，一直到求出f[n]的最佳结果
代码演示
#include
using namespace std;
int f[2022];
int main()
{
for(int i=1;i<=2021;i++)
{
for(int j=i+1;j<=i+21;j++)
{
if(j>2021)
break;
if(f[j]==0)
f[j]=f[i]+j*i/__gcd(i,j);
else
f[j]=min(f[j],f[i]+j*i/__gcd(i,j));
}
}
cout < 第六题 时间显示
❓问题描述
小蓝要和朋友合作开发一个时间显示的网站。
在服务器上，朋友已经获取了当前的时间，用一个整数表示，值为从 1970 年 1 月 1 日 00:00:00 到当前时刻经过的毫秒数。
现在，小蓝要在客户端显示出这个时间。小蓝不用显示出年月日，只需要显示出时分秒即可，毫秒也不用显示，直接舍去即可。
给定一个用整数表示的时间，请将这个时间对应的时分秒输出。
输入描述
输入一行包含一个整数，表示时间。
输出描述
输出时分秒表示的当前时间，格式形如
HH:MM:SS，其中HH表示时，值为 0 到 23，MM表示分，值为 0 到 59，SS表示秒，值为 0 到 59。时、分、秒 不足两位时补前导 0。
题目分析
输入的是毫秒，转化成秒之后就简单了
代码演示
#include
using namespace std;
int main()
{
int h;
cin>>h;
int hh,mm,ss;
h = h%(24*60*60*1000);
hh = h/(60*60*1000)%24;
mm = h/(60*1000)%60;
ss = h/(1000)%60;
printf("%02d:%02d:%02d\n",hh,mm,ss);
return 0;
} 第七题 砝码称重
❓问题描述
你有一架天平和 N 个砝码，这 N 个砝码重量依次是 W1,W2,⋅⋅⋅,WN。
请你计算一共可以称出多少种不同的重量？ 注意砝码可以放在天平两边。
题目分析
类背包问题，设dp[i][j]为前i个砝码里能否称出j的重量
当不添加第i个砝码时dp[i][j]=dp[i-1][j]
当添加第i个砝码在物品端时dp[i][j]=dp[i-1][j-a[i]]
当添加第i个砝码在另一端时dp[i][j]=dp[i-1][j+a[i]]
代码演示
#include
using namespace std;
int dp[200][2000000];
int main()
{
int n;
int a[200];
int sum=0;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
sum+=a[i];
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=sum;j++)
{
dp[i][j]=dp[i-1][j];
if(dp[i][j]==0)
{
dp[i][a[i]]=1;
}
if(dp[i-1][j+a[i]]==1) dp[i][j]=1;
if(dp[i-1][abs(j-a[i])]==1) dp[i][j]=1;
}
}
int ans=0;
for(int j=1;j<=sum;j++)
{
if(dp[n][j]==1) ans++;
}
cout< 第八题 杨辉三角形
❓问题描述
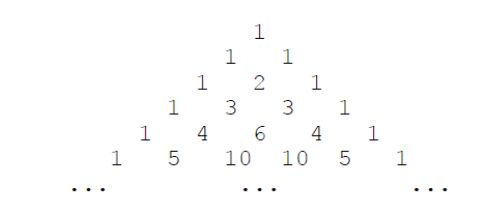
下面的图形是著名的杨辉三角形：
如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列： 1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯
给定一个正整数 N，请你输出数列中第一次出现 N 是在第几个数？
题目分析
我们先观察杨辉三角的特点
第零列 第一列 第二列 第三列 第四列 第五列 第零行 1 第一行 1 1 第二行 1 2 1 第三行 1 3 3 1 第四行 1 4 6 4 1 第五行 1 5 10 10 5 1 由于杨辉三角高度重复且每行都是先增后减的，我们可以忽略右边的部分
第零列 第一列 第二列 第三列 第四列 第五列 第零行 1 第一行 1 第二行 1 2 第三行 1 3 第四行 1 4 6 第五行 1 5 10 此时我们发现规律，每一行右边的数一定比左边的数大，每一列下面的数一定比上面的大
因此我们只要从右往左一列一列二分查找最初出现的位置就可以了
二分查找法可以看看这个
代码演示
#include
using namespace std;
int n;
int C(int x,int k)
{
int ans=1;
for(int i=x,j=1;j<=k;i--,j++)
{
ans=ans*i/j;
if(ans>n)return ans;
}
return ans;
}
int check(int x)
{
int l=2*x,r=max(n,l);
while(l>1;
if(C(mid,x)>=n)r=mid;
else l=mid+1;
}
if(C(r,x)!=n)return 0;
cout<<(int)(r+1)*r/2+x+1;
return 1;
}
int main()
{
cin>>n;
for(int t=17;;t--)
{
if(check(t))break;
}
return 0;
} 第九题 双向排序
❓问题描述
给定序列 (a1,a2,⋅⋅⋅,an)=(1,2,⋅⋅⋅,n)即 ai=i。
小蓝将对这个序列进行 m 次操作，每次可能是将 a1,a2,⋯ ,aqi 降序排列，或者将 aqi,aqi+1,⋯ ,an 升序排列。
请求出操作完成后的序列。
输入描述
输入的第一行包含两个整数 n,m，分别表示序列的长度和操作次数。
接下来 m 行描述对序列的操作，其中第 i 行包含两个整数 pi,qi 表示操作类型和参数。当 pi=0 时，表示将 a1,a2,⋅⋅⋅,aqi 降序排列；当 pi=1 时，表示将 aqi,aqi+1,⋯ ,an 升序排列。
输出描述
输出一行，包含 n 个整数，相邻的整数之间使用一个空格分隔，表示操作完成后的序列。
题目分析
使用sort进行排序，只能过60%，有大佬会可以教教我
代码演示
#include
using namespace std;
int cmp1(int x,int y)
{
return x>y;
}
int main()
{
int n,m;
cin>>n>>m;
int a[n+2];
for(int i=0;i>p>>q;
if(p==0)
{
sort(a,a+q,cmp1);
}
if(p==1)
{
sort(a+q-1,a+n);
}
}
for(int i=0;i 第十题 括号序列
❓问题描述
给定一个括号序列，要求尽可能少地添加若干括号使得括号序列变得合法，当添加完成后，会产生不同的添加结果，请问有多少种本质不同的添加结果。
两个结果是本质不同的是指存在某个位置一个结果是左括号，而另一个是右括号。
例如，对于括号序列 ((()，只需要添加两个括号就能让其合法，有以下几种不同的添加结果：()()()、()(())、(())()、(()()) 和 ((()))。
输入描述
输入一行包含一个字符串 s，表示给定的括号序列，序列中只有左括号和右括号。
输出描述
输出一个整数表示答案，答案可能很大，请输出答案除以 1000000007的余数。
题目分析
动态规划，好难呀~不会了
总结
暴力杯不是原来的暴力杯了，全是动态规划了，今年应该也有动规大题，大家可以练一练动规题目
本人不才，如有错误，欢迎各位大佬在评论区指正。有帮助的话还请【关注➕点赞➕收藏】，不行的话我再努努力