备战蓝桥,冲击省一 二分查找法 看完你就会了

作者简介：大家好，我是Ceylan_，可以叫我CC ❣️    
个人主页：Ceylan_的博客
博主信息：平凡的大一学生，有着不平凡的梦

⚡希望大家多多支持一起进步~❤️
若有帮助，还请关注➕点赞➕收藏，不行的话我再努努力

目录

一、猜数字

简单查找

二分查找法

 二、二分查找法介绍

固定模板

二分法时间复杂度

三、练习：

力扣704. 二分查找

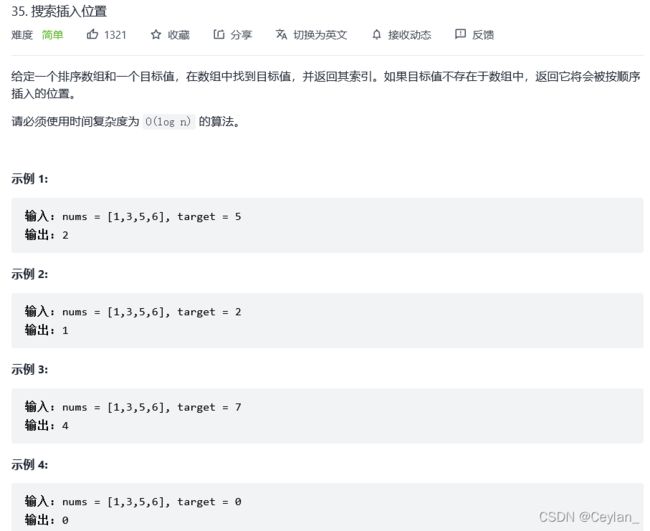
力扣35. 搜索插入位置

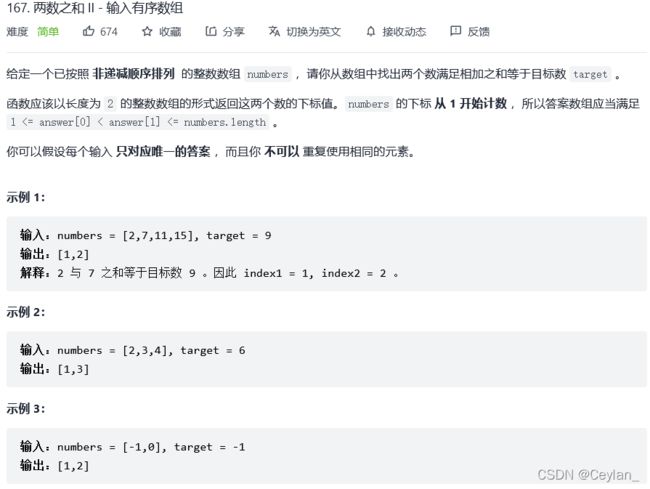
力扣167. 两数之和 II - 输入有序数组

---

​

一、猜数字

我随便想一个1~100的数字，你的目标是以最小的次数猜到这个数字。你每一次猜测后，我都会说小了、大了或对了。

简单查找

最简单的方法，就是你从1开始依次往上猜，每一次查找只能排除一个数字。

是1吗？                                                                 小了      

1

2

3

...

...

100

 

 是2吗？                                                                   小了      

1

2

3

...

...

100

如果我想的数字是99，那么你需要猜99次才能猜到。显而易见的，这是一种很愚蠢的查找方法。

二分查找法

这是一种更好的猜法，第一个数猜50。

  是50吗？                                                                 小了      

1

...

50

51

...

100

虽然没有猜中，但是你一下排除了一半的数字！你知道1~50都小了，接下来，你猜75（50和100中间的数）

   是75吗？                                                                         大了      

50

51

50

...

74

75

大了，剩下的数字又排除了一半！接下来，你猜63（50和75中间的数）。

   是63吗？                                                                      对了      

这就是二分查找法，恭喜你已经学会了！在这个游戏中，每次猜测排除的数字个数如下

​

不管我心中想到哪个数字，你都可以在7步之内猜到，这就是二分查找法的优点。

二分查找法，每次都能排除一半的数字

我们试一试用代码表示：

#include
int main()
{
	int l=0,r=100,target;
	scanf("%d",&target);
	while (l < r)
	{
	    int mid =(r-l)/2+l;
	    if(mid==target)
	    {
			printf("你的数字为%d",mid);
			return 0;
		}
	    else if (mid>target)
		{
			r=mid+1;
		}      
		else
		{
			l=mid-1;
		}
	}
}

 二、二分查找法介绍

固定模板

我们来看一看二分法的固定模板

int binarySearch(vector nums, int left, int right, int x)
{
       int mid;//mid为中点
       while (left<=right)
       {
              mid = left + (right - left) / 2;//取中点
              if (nums[mid] == x) return mid;// 找到x，返回下标
              else if (nums[mid]>x)//中间的数大于x
              {
                    right = mid - 1;//往左子区间[left,mid-1]查找
              }
			  else 					//中间的数小于x
			  {
                    left = mid + 1; //往右子区间[mid+1,right]查找
              }
       }
       return -1;//查找失败，返回-1
}

 为什么用【mid = left + (right - left)/2】而不用【mid=(right+left)/2-left】呢？

当left和right都很大的时候，可能会造成越界

我们可以这样理解二分查找法

【left，right】—— 用于标记观察查找范围的位置

【while (left<=right)】—— 只要范围没有缩小到只剩一个元素就继续查找

【 if (nums[mid]>x) 】—— 若中间值大于目标值——【right = mid - 1;】改变右端点，往左子区间[left,mid-1]查找

【 if (nums[mid]若中间值小于目标值——【left = mid + 1;】改变左端点，往右子区间[mid+1,right]查找

二分法时间复杂度

一般而言，对于包含n个元素的列表，用简单查找最多需要n步，用二分查找法最多需要log2n步。

二分查找法的运行时间为对数时间，是一种很高效的算法。

三、练习：

力扣704. 二分查找

​

class Solution {
public:
    int search(vector& nums, int target) {
        int left=0;
        int right=nums.size()-1;
        int a;
        while(left<=right)
        {
            a=(right-left)/2+left;
            if(nums[a]==target)
                return a;
            else if(nums[a]>target)
                right=a-1;
            else
                left=a+1; 
        }
    return -1;
    }
};

力扣35. 搜索插入位置

​

class Solution {
public:
    int searchInsert(vector& nums, int target) {
        int n = nums.size();
        int l=0,r=n-1;
        while(l<=r){
            int mid=l+(r-l)/2;
            if(nums[mid]

力扣167. 两数之和 II - 输入有序数组

​

class Solution {
public:
    vector twoSum(vector& numbers, int target) {
        for(int i=0;itarget)
                {
                    right=mid-1;
                }
                else
                {
                    left=mid+1;
                }
            }
        }
        return {-1, -1};
    }
};

每日金句

生活是一面镜子。你对它笑,它就对你笑;你对它哭,它也对你哭

​

     本人不才，如有错误，欢迎各位大佬在评论区指正。有帮助的话还请【关注➕点赞➕收藏】，不行的话我再努努力

CSDN社区 《博客新星》活动，官方大力扶持新人创作，只要参与其中并发布原创就有机会获得官方奖品：精品日历、新程序员杂志、CSDN帆布包、CSDN定制款手机壳，快来参与吧！链接直达 https://bbs.csdn.net/topics/605597781